Adele
DESIGN PAPER 1 (THEORY) GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
DESIGN
PAPER 1 (THEORY)
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
INSTRUCTIONS AND INFORMATION
- This question paper consists of SIX questions.
- There are three choice questions in this question paper. Read the options carefully.
- This question paper consists of THREE sections:
SECTION A: Design literacy (30 marks)
QUESTIONS 1 to 3
SECTION B: Design history (30 marks)
QUESTION 4
SECTION C: Design in a sociocultural/environmental and sustainable context (40 marks)
QUESTIONS 5 and 6 - Read the requirements of each question carefully.
- Answer in full sentences and avoid the listing of facts. Do NOT answer in tabular form.
- Use the mark allocation to determine the time to be spent on each question.
- Do NOT repeat the same facts and examples in different questions.
- Write neatly and legibly
QUESTIONS
SECTION A: DESIGN LITERACY
QUESTION 1: 'UNSEEN' EXAMPLES
Answer EITHER QUESTION 1.1 OR QUESTION 1.2.
1.1
FIGURE A: The Daddy Cool Bling Bar by Studio Botes
(South Africa), 2013.
Analyse the use of the following element and principles in FIGURE A above:
- Balance
- Focal point
- Rhythm
- Contrast
- Shape (5 x 2) [10]
OR
1.2
FIGURE B: Eclectic and recycled range of furniture designs
by Reform Studio (Egypt, Africa), 2015.
With the belief that design can solve problems, we developed textile threads from reused plastic bags, which now form the basis of its designs. [Reform Studio] |
Explain the use of the following design terms in FIGURE B above:
- Eclectic
- Truth to materials
- Minimalism
- Form follows function
- Upcycle (5 x 2)
[10]
QUESTION 2: COMMUNICATION THROUGH DESIGN
FIGURE C: Because I am a girl campaign poster
by Plan International (Canada), 2015.
2.1 Briefly discuss the message conveyed by the poster in FIGURE C above.
Refer to the following in your discussion:
- Use of colour (2)
- The use of imagery in the poster (3)
- The font in the slogan of the campaign (Because I am a girl) (3)
2.2 Discuss how the poster in FIGURE C above clearly reflects stereotyping. (2)
[10]
QUESTION 3
Answer EITHER QUESTION 3.1 OR QUESTION 3.2.
3.1 Refer to FIGURE D and FIGURE E below and answer the questions that follow.
| | |
| FIGURE E: Pouffe Dress by Emmanuel Nunez (South Africa), 2015. | FIGURE D: Dress by Issey Miyake (Japan), 2013. |
Write an essay of at least 200–250 words (one page) in which you compare FIGURE D with FIGURE E.
Refer to the following:
- Inspiration/Influences
- Form
- Pattern
- Colour
- Avant-garde (5 x 2) [10]
OR
3.2
. | |
| FIGURE F: Basilica of St Paul's outside the Walls (Rome), 4th century AD | Interior of Basilica of St Paul's outside the Walls (Rome), 4th century AD. |
| FIGURE G: Notre Dame du Haut by Le Corbusier (France),1955. | Interior of Notre Dame du Haut by Le Corbusier (France),1955. |
Write an essay of at least 200–250 words (one page) in which you compare the ancient classical basilica in FIGURE F with the contemporary church in FIGURE G above. Alternatively you may compare any Classical building (that you have studied) with any contemporary building.
Refer to the following in your essay:
- Function
- Structure
- Use of light
- Building materials
- Decoration (5 x 2)
[10]
TOTAL SECTION A: 30
SECTION B: DESIGN HISTORY
QUESTION 4
4.1
Choose any TWO movements in the list below and write an essay of at least 400–450 words (two pages) in which you debate whether their designs reflect the above quote. Support your answer by referring to the aims and stylistic characteristics of your chosen movements. Refer to at least ONE designer from each movement and discuss at least ONE design by each designer to support your statements.
- Arts and Crafts
- Rococo
- Scandinavian Design
- Ancient Greek
- Art Nouveau
- Modernism
- Renaissance
- Deconstruction
- Ancient Roman
(20)
4.2
| FIGURE H: Worcester Porcelain Teapot inspired by Piet Mondrian, De Stijl (England), 1944. | FIGURE I: Porcelain tea set by Clarice Cliff, Art Deco (England), circa 1930. |
Write a comparative essay of 200–250 words (one page) in which you discuss whether the above two designs reflect the mood of the design movements they represent.
Refer to the following to support your answer:
- Inspiration
- Aims
- Line
- Shape
- Decoration (5 x 2)
(10)
TOTAL SECTION B: 30
SECTION C: DESIGN IN A SOCIOCULTURAL/ENVIRONMENTAL AND SUSTAINABLE CONTEXT
QUESTION 5
Answer EITHER QUESTION 5.1 OR QUESTION 5.2.
5.1
FIGURE J: Anti-tobacco poster by the World Health Organisation
(Canada), 2012.
5.1.1 Explain how the message in the poster above is communicated by using the following:
- Imagery
- Design layout
- Use of font (3 x 2) (6)
5.1.2 Write an essay of at least 300–350 words (one and a half pages) in which you name and discuss the work of ONE South African contemporary designer/design group AND ONE international contemporary designer/design group who address sociocultural issues in their work.
Refer to the following in your discussion:
- Aims that relate to the concept of sociocultural design
- Methods and processes
- A discussion of ONE example that reflects social responsibility
You may NOT refer to any designer(s)/design group(s) that you have discussed previously or design examples used in this question paper. (14)
[20]
OR
5.2
5.2.1 Write an essay of at least 200–250 words (one page) for a tourist brochure about a traditional craft practised in South Africa.
Refer to the following in your essay:
- The traditional history of the craft
- The value of practising this craft
- Functions
- Materials, methods and processes
- A description of ONE example, as well as the name(s) of the indigenous cultural community or craftsperson that produced it (10)
5.2.2 Write an essay of approximately 200–250 words (one page) on any ONE South African contemporary designer/design group, who uses traditional craft techniques/materials in a modern way and, at the same time, empower individuals or communities.
Use the following structure when answering the question:
- Name of designer/group and his/her/their design product(s)
- A detailed description of how traditional techniques/methods and material have been applied to contemporary design. Refer to specific examples to support your statements.
- Discuss the sociocultural contribution of the design(s)
You may NOT refer to any designer/design group that you discussed previously or design examples that appear in this question paper. (10)
[20]
QUESTION 6
6.1
FIGURE K: Neck piece by Mariana Acosta (Mexico),
Precious Waste contemporary jewellery collection, 2015.
Precious Waste uses materials such as PET bottles, discarded CDs, egg cartons, old books, scrap metals, tetra packs, VHS videotapes and paper tubing to transform them into valuable design accessories. |
6.1.1 Discuss TWO characteristics of sustainable design. (2)
6.1.2 Identify and discuss TWO materials that you can use as a sustainable designer. Explain the sustainability of these materials in your discussion. (4)
6.2 Write an essay of at least 300–350 words (one and a half pages) in which you discuss the work of ONE South African contemporary designer/design agency/studio and ONE international contemporary designer/design agency/ studio whose work explores sustainable sources/materials and transforms them into significant design products.
Refer to the following in your discussion:
- Name of the designer/design group and his/her/their design product(s)
- A discussion of ONE example
- Transformation of its sustainable material
- Its impact on the environment
You may NOT refer to any designer/design company that you have discussed previously or design examples referred to in this question paper. (14)
[20]
TOTAL SECTION C: 40
GRAND TOTAL: 100
DESIGN PAPER 1 (THEORY) GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
DESIGN
PAPER 1 (THEORY)
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
MEMORANDUM
SECTION A: DESIGN LITERACY
'UNSEEN' EXAMPLES
ANSWER EITHER QUESTION 1.1 OR QUESTION 1.2.
QUESTION 1 [10 Marks]
1.1 (Allocate a maximum of two marks per element and principle)
- BALANCE
The images are arranged in a bilateral symmetrical balanced manner to create a sense of order and calmness. ? The clustering of the images in a circular form around a large central motif shows off radial balance. ? - FOCAL POINT
The DC circular pendant on a chain is the predominant focal point as it is placed right in the centre. ? It is clearly the biggest image in the illustration. ? The two points of the heart also direct the eye to the DC pendant. ? - RHYTHM
The repeated images, for example hats, sneakers, cellphones and rings make your eyes wander in a vertical, horizontal and circular movement. ? The repeat of many circular images, for example the rings and the central pendant and the flower image also contribute to creating a circular rhythm. ? - CONTRAST
The plain, flat background contrasts starkly with the numerous images and with the fine detail on many of them. It creates a lively, almost shimmering surface. ? Small motifs such as the little shiny stars contrast with larger motifs like the hat and the money bag also activating the surface. ? This shimmery feel communicates opulence and wealth. ? - SHAPE
The images are all flat and simplified to create a clear and clean composition that reads easily. ? The money bag, hat, sneaker and bottle are organic shapes that convey movement whilst the cellphone, diamond and other gems are geometric, stabilising this movement. ?
Credit must be given to any other valid statements.
Q.1.1 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (10) |
Lower Order | Remember, Recall, Recognise | 30% | 1.1 | 2 |
Understand, Explain, Describe | 1.1 | 1 | ||
Middle Order | Apply, Implement, Organise | 40% | 1.1 | 4 |
Higher Order | Analyse, Interpret | 30% | 1.1 | 1 |
Reflect, Judge | 1.1 | 1 | ||
Synthesis | 1.1 | 1 |
OR
1.2 [Allocate a maximum of 2 marks per design term for a total of 10 marks]
- ECLECTIC
The term eclectic means to borrow from a variety of design styles/periods, to form a new, unique design. ? The simple rectangular form of the bench makes reference to the Bauhaus and Modernist ideals of Minimalism and 'Less is More'. ? Another possible reference is to Scandinavian Design's emphasis on functionality, clean lines, light materials and bright colours and their use of sustainable materials. ? The Postmodernist belief in environmentally sound designs is also visible in this product's use of woven recycled plastic. ? - TRUTH TO MATERIALS
In keeping with the philosophy of 'truth to materials' the wood of the bench is kept unpainted to reflect the beauty of its natural state. ? The colour and grain of the wood is left visible linking the bench to nature. ? - MINIMALISM
The meaning of the term Minimalism implies “Less is More” i.e. the designer has used the 'bare necessities' ? to create a clean and streamlined form. ? - FORM FOLLOWS FUNCTION
The simple form of the design emphasises its function. ? All emphasis is placed on functionality and decoration is economically applied to emphasise the simple geometric form. ? - UPCYCLED
The fibres of the textile section of the bench are formed from recycled plastic bags. ? The plastic bags have been upcycled to achieve a new purpose, i.e. becoming upholstery. ?
Credit must be given to any other valid statements.
Q.1.2 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (10) |
Lower Order | Remember, Recall, Recognise | 30% | 1.2 | 1 |
Understand, Explain, Describe, Classify | 1.2 | 2 | ||
Middle Order | Apply, Implement, Organise | 40% | 1.2 | 4 |
Higher Order | Analyse, Interpret | 30% | 1.2 | 1 |
Reflect, Judge | 1.2 | 1 | ||
Synthesis, Justify | 1.2 | 1 |
COMMUNICATION THROUGH DESIGN
QUESTION 2 [10 marks]
2.1 (Allocate 8 marks)
(Allocate 2 marks)
- Use of colour
This message seems to be set within an African context because of the sub-Saharan background which is brown, dry with very little greenery. ? The use of the colour black symbolises the doom, dread, emptiness and sadness of poverty. ? The contrast of the black image of the girl in the left image in comparison to the brightly coloured figure of the girl in the image on the right could possibly symbolise the difference in a future with an education versus one without an education. ?
(Allocate 3 marks) - The use of imagery in the poster
The message of the poster conveys the importance of educating little girls as equally important as educating little boys. ? This is communicated through the image of the little girl in the foreground and the image of the little boy in the background on both posters. ? Often male children are given an opportunity to get an education as they are traditionally viewed as future breadwinners. ? The girl child, on the other hand, is viewed as a future mother and wife with little importance and therefore there is no need for education. ? The little barefooted girl in the image on the left conveys poverty. ?
(Allocate 3 marks) - The font in the slogan of the campaign (Because I am a girl)
The “I” in the slogan is elongated/stretched ? which could communicate that by empowering the girls with education you are giving them the power to reach for the sky. ? In attaining dreams and allowing them to have a bright future. ? The font is slightly childlike to show her vulnerability. ? The size and colour of the word 'girl' is highlighted to emphasise the importance of educating girls. ? The pink red colour of the font also stereotypes against girls. ?
(Allocate 2 marks)
2.2 This poster in FIGURE C assumes that all men have access to education ? and that all rural black girls are disadvantaged and destined to fall pregnant, without getting an education. ? The poster stereotypes against black girls as there are girls from other race groups that are also affected by poverty. ?
Credit must be given to any other valid statements.
Q.2 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (10) |
Lower Order | Remember, Recall, Recognise, Name | 30% | 2.1 | 2 |
Understand, Explain, Describe, Classify | 2.1 | 1 | ||
Middle Order | Apply, Implement, Organise | 40% | 2.1 2.2 | 3 1 |
Higher Order | Analyse, Compare, Interpret | 30% | 2.1 | 2 |
Evaluate, Reflect, Judge | 2.2 | 1 |
QUESTION 3 [10 marks]
ANSWER EITHER QUESTION 3.1 OR QUESTION 3.2.
(OPTION 1)
3.1 [10 marks]
The dress in FIGURE D could be inspired by the flowing attire of Arabian women. ? The use of boots and strong bands of black in the pattern evokes associations with uniforms/armour of soldiers as well as with the 'Sub Saharan emo' subculture (use of a lot of black in the clothing with black boots). ? FIGURE E is an eclectic design influenced by many styles and movements, for example, the linear texture on the surface of FIGURE E is reminiscent of Indonesian batik cloth, while the strong diamond and triangular patterns are Xhosa Shweshwe in style. ? The short, puffy skirt is funky, girlish and contemporary in inspiration. ? The pattern on FIGURE D is modern and could be inspired by machine-age movements such as the Bauhaus and De Stijl as it consists of straight lines and geometric, block-like shapes. ?
FIGURE D's forms are large and sweeping, consisting of a heavy, flowing and loose skirt form and a block-like top whereas FIGURE E's forms are small and crisp. ? The top of FIGURE E is tight fitting, contrasting with the skirt that is short and puffy expressing a girlish youthfulness. ? The large, sweeping forms of FIGURE D, in comparison evoke images of traditional ethnical tribal wear. ?
The repetition of thin, straight horizontals and thick horizontal and vertical bands of black create a striking plaid-like pattern. ? The pattern on FIGURE E, on the other hand is more organic and African in style due to the repeated tie-dye or batik texture and the repetitive small triangles and diamonds. ?
The heavy black bands and strong red primary colour of FIGURE D creates a dramatic, eye-catching design. ? FIGURE E also consists of a dominant red but this red is deeper and more subdued. ? The contrasts of yellow and white triangles form areas of light contrasts creating a more active surface than that of FIGURE D. ? The contrast between the red and black creates a dynamic colour aesthetic. ?
Both dresses can be considered avant-garde. FIGURE D fuses a traditional dress form with modern machine-age pattern and combines this with industrial-like black boots to create an almost futurist image. ? FIGURE E uses a traditional African print to create a funky modern dress. ? The combination of a western felt hat on top of an African headscarf, as well as the inclusion of high heels and an ethnic style necklace, accentuates the eclecticism of the design. ?
Credit must be given to any other valid statements.
NOTE: A maximum of ONLY 3 marks may be allocated for tabular comparison responses. Use the cognitive level grid as a guideline for your marking
Q.3.1 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (10) |
Lower Order | Remember, Recall, Recognise | 30% | 3.1 | 1 |
Understand, Explain, Describe | 3.1 | 2 | ||
Middle Order | Apply, Implement, Organise | 40% | 3.1 | 4 |
Higher Order | Analyse, Compare, Interpret | 30% | 3.1 | 1 |
Evaluate, Reflect | 3.1 | 1 | ||
Create, Synthesise | 3.1 | 1 |
OR
(OPTION 2)
3.2 [10 marks]
The Notre Dame du Haut functions as a contemporary place of worship dedicated to the Virgin Mary. ? The Basilica of St Paul is also a place of worship in honour of St Paul whose tomb was placed directly under the altar. It is a Roman basilica, the first model built for a Christian church. ?
Typical of the Roman Basilica the Basilica of St Paul's main structure is a simple rectangle with three aisles, with the main one in the centre (the nave) built higher than the sides and including windows (a clerestory) above the side aisles. ? The repeated vertical columns and a horizontal entablature create a very stable structure, typical of classical architecture. ? The structure of the Notre Dame du Haut, on the other hand, is very irregular, sculptural and organic reminiscent of heavy rock formations. ? The semi circular apse at the top end of the basilica softens the general rectilinearity. ? The Notre Dame du Haut, on the other hand, consists of many curved edges balanced by a few verticals. ? The roof of the Notre Dame du Haut reminds one of a slab of rock and appears to be floating from the inside. A space of several centimetres between the roof and the walls allowing daylight to enter enhances this floating feeling. ?
The Basilica of St Paul acquires its soft, glowing light from the row of windows in the clerestory, ? whereas the Notre Dame du Haut achieves light from rectangular openings deeply set in the thick walls creating a spiritual and meditative atmosphere inside the building. ? The Basilica's light is gold in colour, glorifying God's Kingdom whereas the light in the Notre Dame is white, glorifying God's purity. ?
The Basilica is constructed from traditional natural building materials such as marble, alabaster and granite, whereas the Notre Dame du Haut is constructed from both white stone and rugged concrete. ? The stone that dominates the Basilica gives it a solid, strong feeling. ? The concrete and stone of the Notre Dame du Haut also exudes solidity and earthiness. ? The floor of the chapel follows the natural slope of the hill down towards the altar. Certain parts, in particular those upon which the interior and exterior altars rest, are of beautiful white stone from Bourgogne, as are the altars themselves. The towers are constructed of stone masonry and are capped by cement domes. ?
Many surfaces of the Basilica are highly decorated with golden and coloured glass mosaics illustrating religious imagery such as the Apocalypse of John, with the bust of Christ in the middle flanked by the 24 doctors of the church, surmounted by the flying symbols of the four Evangelists. ? This decoration is very sensual and expressive. ? The wall surfaces of the Notre Dame du Haut in contrast, are unadorned and painted white, reflecting simplicity and purity. ? The roof is also a neutral black contributing to this general mood of seriousness. ? The surfaces of the Basilica are smooth whereas the interior and the exterior of the chapel are surfaced with mortar sprayed on with a cement gun and then white-washed giving them an organic feel. ?
Credit must be given to any other valid statements or a comparison of a classical and contemporary building that the candidate has studied.
NOTE: A maximum of ONLY 3 marks may be allocated to tabular comparison responses. Use the cognitive level grid as a guideline for your marking.
Q.3.2 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (10) |
Lower Order | Remember, Recall, Recognise | 30% | 3.2 | 1 |
Understand, Explain, Describe, Classify | 3.2 | 2 | ||
Middle Order | Apply, Implement, Organise | 40% | 3.2 | 4 |
Higher Order | Analyse, Compare, Interpret | 30% | 3.2 | 1 |
Evaluate, Reflect | 3.2 | 1 | ||
Create, Synthesise, Justify | 3.2 | 1 |
TOTAL SECTION A: 30
SECTION B: DESIGN HISTORY
QUESTION 4 [30 marks]
4.1 Allocate 20 marks in total)
(Allocate 10 marks for each movement. Please note that only one mark can be allocated for the name of a designer and product for each movement. Please use the cognitive level grid as a guideline for your marking.)
This memo supplies an answer for the following two possibilities:
ARTS AND CRAFTS AND DECONSTRUCTIVISM
Arts and Crafts
The above quote is by William Morris one of the founders of the Arts and Crafts movement. The Arts and Crafts movement aimed to place an emphasis on the natural unity between form, function and decoration, ? keeping their designs simple, elegant and functional. ? They aimed to turn around the poor taste and inferior quality of mass-produced goods, which were over-designed and full of unnecessary detail. ? The movement aimed to condemn the capitalist industrial production that was based on making money. ? A number of artists and craftspeople were involved and it marked the beginning of time where an importance was attached to the design of everyday objects. ? During the Victorian era many factory produced designs were designed by the machine operators or by the factory owners. ? Their designs were of poor taste and full of unnecessary detail. As the above quote states; Morris developed the view that design should aim to be both beautiful and functional. A focus on quality and craftsmanship and the use of the natural materials characterised the Art and Craft designs as honest, meaning that you can see the joints and manufacturing marks instead of hiding or covering them with decorative elements. ? Designs were kept simple, elegant and functional and stained glass, wood, textiles and natural brick were popular materials. ?
All paper, inks and textile designs were produced by hand, using organic materials. This is a key characteristic of Arts and Crafts design and the result is complete control of the quality and production of design. ? The Arts and Crafts style characteristics harked back to medieval architecture and tapestries, illuminated manuscripts and rustic styles of decoration and furniture. ? Their subject matter was drawn from the plants, animals and the birds of nature, particularly in wall paper and textile design. ?
William Morris began printing on calico when he purchased the Merton abbey works in 1881. True to the aims and characteristics of the movement Morris aimed to produce an item that was beautiful, hand crafted and made in such a way that it would benefit the workers. ? Fabrics were dyed using only the highest quality, natural dyes based on herbal recipes. ? The printed textile from Morris and Co. 1884 produced in Merton Abbey was dyed using the indigo discharge method. The method involves first dying the calico an indigo blue shade and then removing the areas where the design appears with bleach. Finally the fabric is dyed again using red and yellow resulting in a deep palette of reds, oranges, purples, greens and blues. ? The textile design is based on natural motifs (flowers, vines and leaves). A sense of perspective is achieved by overlapping the flowers and stems. Texture was achieved through patterning. Gentle wavy lines and regularly curving patterns of leaves and flowers along with stylised scroll leaf pattern create an aesthetically appealing design. ? This example is both useful and beautiful.
Deconstructivism
Contradictory to the above statement instead of focusing on the function and the construction and aesthetics of designs, Deconstructivist designers focused on exploring the relationship between the different parts of a design. ? The resulting style resembles designs that are irregular and literally fragmented. ? 'Unnecessary' lines and forms are created for the sake of creating new and original structures. ?
The aims of Deconstructivism are based on the writings of French philosopher Jacques Derrida. Derrida explores uncertainties and opposites that are in a state of instability and the unseen relationships between all things rather than the function and usefulness of parts. ? Their designs aimed to pull things apart in order to investigate the relationship between the parts. ? Deconstructivism aims to question structures and forms that have existed and been accepted over the ages. ? These basic norms are subverted and disturbed. Lines and shapes become fluid and often defy gravity or visual stability. ?
Frank Gehry is a Deconstructivist architect who uses highly unconventional materials in unusual ways. Gehry has broken new ground in architectural design by exploring the stylistic characteristics of Deconstructivism in the way he manipulates shape and texture. ? The Guggenheim Art Museum in Bilbao Spain, is an iconic example of Deconstructivism. ? Its function/'use' as an art museum is subsidiary and the fact that it does not conform to normal building specifications contradicts the latter part of the above statement. Its lack of conformity allows the building to be considered ugly therefore not believed to be beautiful; it disregards the norms of a Classical Western art museum. ? The unconventional exterior of the building is clad in half millimetre thick titanium panels that reflect light at all times of the day and night interspersed by limestone and glass, providing transparency and a neutral colour. The titanium does not oxidise but is a most unusual and controversial cladding material for buildings. ? These materials are chosen for their unconventional characteristics rather than for their 'beauty' or 'usefulness'. ?
The Guggenheim Art museum designed in the Deconstructivist style characteristically has no conventional straight line and right-angled corner in the design creating an unstable composition. ? These lines and forms are not essential to the function of the building but are used for the sake of exploring a new architectural style based on the relationship between opposites. ? In conclusion the Deconstructivist movement is the antithesis of the above quote. ?
Credit must be given to any other valid statements.
Q.4.1 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (20) |
Lower Order | Remember, Recall, Recognise, Name | 30% | 4.1 | 2 |
Understand, Explain, Describe, Classify | 4.1 | 4 | ||
Middle Order | Apply, Implement, Organise | 40% | 4.1 | 8 |
Higher Order | Analyse, Compare, Interpret | 30% | 4.1 | 2 |
Evaluate, Reflect | 4.1 | 1 | ||
Create, Synthesise, Justify | 4.1 | 3 |
4.2 [10 marks] 
Inspiration
De Stijl was founded by a group of Dutch designers who were inspired by the Dutch tradition of logic, severity and clarity. ? Art Deco was inspired by a societal fascination with ancient exotic societies such as Ancient Egypt, Aztec Civilizations and Africa. ?
Aims
Both Art Deco and De Stijl design movements occur between the two World Wars. In a desperate attempt to escape the horrors of a war torn society, the Art Deco movement aimed to create an alternative reality of exoticism, glamour, elegance and luxury. ? The De Stijl movement, on the other hand, did not attempt to escape reality but attempted to find the essence of reality through geometric abstraction. ? They aimed to restore order after the chaos of the World War by exploring abstraction and reducing the design elements to a universal language that focused on geometry. ?
During the Art Deco age, machinery was used extensively to create new products which, like the tea set of Clarice Cliff, aimed to meet the day to day needs of city dwellers. ? The culture of the industrial revolution had increased urban population which meant there was a demand for machine-made goods and entertainment at affordable prices and a need to escape 'everyday life'. ?
Line
The De Stijl tea pot's use of vertical and horizontal line is typical of the movement's rigidity. ? They moved away from tradition and used geometric bold lines creating a simple, clean effect. ? The line of the Art Deco tea pot is more varied and expressive with the use of wavy and straight lines creating a more organic feel. ?
Shape
Characteristic of Art Deco is the tea pot's use of simple modernist shapes. The edges are clean, straight and zigzagged edges creating dynamic, streamlined shapes. ? On the other hand the De Stijl movement established the use of pure, geometric shapes. ? This characteristic is evident in the De Stijl tea pot which displays stark right angled shapes. ?
Decoration
De Stijl's decoration is abstract, evolving from their focus on geometry and mathematics. ? Instead of traditional decoration as still evident in the Art Deco tea set, it broke with all design and art conventions. ? The “De Stijl tea pot” shows the simplification of decoration into 'basic' building blocks of visual expression, geometric forms, vertical and horizontal lines and only the three primary colours, black and white. ? De Stijl rejected all reference to tradition and external reality and looked to architecture and urban planning for decoration. ? Contrary to this, the Art Deco tea pot shows recognisable subject matter such as the sun, mountains and a flower, but typical of the movement, these images are stylised, decorative and two-dimensional. ?
Credit must be given to any other valid statements.
NOTE: A maximum of ONLY 3 marks may be allocated for tabular comparison responses. Use the cognitive level grid as a guideline for your marking.
Q.4.2 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (10) |
Lower Order | Remember, Recall, Recognise, Name | 30% | 4.2 | 1 |
Understand, Explain, Describe, Classify | 4.2 | 2 | ||
Middle Order | Apply, Implement, Organise | 40% | 4.2 | 4 |
Higher Order | Analyse, Compare, Interpret | 30% | 4.2 | 1 |
Evaluate, Reflect, Judge | 4.2 | 1 | ||
Create, Synthesise, Justify | 4.2 | 1 |
TOTAL SECTION B: 30
SECTION C: SOCIO-CULTURAL/ENVIRONMENTAL AND SUSTAINABLE CONTEXT QUESTION 5 [20 marks]
ANSWER EITHER QUESTION 5.1 OR QUESTION 5.2.
(OPTION 1)
5.1 [20 marks]
5.1.1 (Allocate 6 marks)
(Allocate 2 marks)
- Imagery
- The poster is conveying the message that smoking is bad for one's health. ?
- The image of teeth decaying is a very repulsive image successfully conveying the negative impact on one's health. ?
- The skin around the teeth looks inflamed contributing to this anti-tobacco message. ?
(Allocate 2 marks)
- Design Layout
- The image is placed strategically so that it appears as if a hand reaching for a cigarette can be bitten. ?
- This also emphasises the danger of smoking. ?
- The image of the cigarette box is large and dominant making it the focal point, confronting the viewer. ?
- The top quarter of the poster consists of a clear message in a white text block against a dark background also attracting the eye of the viewer. ?
(Allocate 2 marks)
- Use of Font
- A simple, sans serif font is used which helps to convey the message in a clear and direct way. ?
- The use of capital letters emphasise the importance of the message conveyed. ?
- The white font contrasts with the black background, further emphasising the importance of the message. ?
Credit any other valid statements.
5.1.2 Allocate 14 marks in total
(Allocate 7 marks per case study)
Allocate 1 mark for the name of the designer and the name of the product.
ONE CONTEMPORARY SOUTH AFRICAN DESIGNER/DESIGN GROUP:
Necklace from felt and beads by Zimele Social Empowerment craft group ?
Aims:
- Zimele focuses on developing community self-reliance through crafts. ?
- Zimele is a non-profit organisation based in Pietermaritzburg that was founded in 2007 by Rosetta Stander. Determined to break the cycle of 'hand-out dependency' and basing her model on highly successful schemes in India, she created Zimele, meaning “people stand on their own feet” in Zulu. ?
- Zimele is a non-profit organisation that acts as a facilitator, not just feeding people for a day but leading them towards belief in their personal ability to work their way out of poverty. ?
- Zimele's aim is to focus on the individual's journey to self-worth, self-realisation, and finally sustainable self-sufficiency. People are therefore able to contribute fully according to their individual strengths on a community level for the ultimate benefit of both the individual and the wider community. ?
Methods and processes:
Zimele is currently implementing its programmes in all 11 districts of KwaZulu-Natal with approximately 3500 women actively involved with Zimele. ?
The Zimele model works to:
- empower women by unlocking skills, resources, support systems and networks, and
- create new opportunities such as local and international markets and links to government programmes ?
Zimele pursues this vision through providing women with the knowledge, skills, resources and support networks to sustain themselves and their families. ?
Women are traditionally excellent crafters within Zulu society and many rural women have existing craft skills. ?
Through Zimele they are trained to make high quality items, using their incredible talents. They work with fabric, felt and beads to make a range of stationery, bags, decorations, home ware and jewellery. ? The range includes bags, décor, homeware and jewellery made from felt, beadwork and fabric. ?
The training and materials are free of charge, although the women are expected to purchase the tools/equipment needed such as needles, scissors and pliers. ? Once the products are of a good standard, the women purchase the raw materials and Zimele pays for the items that they make on order. ?
A discussion of ONE example that reflects social responsibility
The Necklace made from felt and beads consists of differently sized, colourful circular discs ? hanging from different strands of string/twine to create a playful and fun necklace. ?
ONE INTERNATIONAL DESIGNER/DESIGN GROUP
Makoko floating school designed and built by NLE in collaboration with the Makoko Waterfront Community, in Lagos State. ?
Nigerian architect Kunlé Adeyemi, ? the founder and principal of NLÉ Works, in collaboration with the Makoko Waterfront Community, conceived, designed and built the floating school, in Lagos State. The project was initially self-funded by NLE and later received research funds from Heinrich Boll Stiftung as well as funds for its construction from the UNDP/Federal Ministry of Environment Africa Adaptation Programme (AAP).
Aims:
Makoko Floating School is a 'prototype' building structure for NLÉ's proposed 'Lagos Water Communities Project' and its 'African Water Cities' research project. ?
Makoko Floating School addresses physical and social needs in view of the growing challenges of climate change in an urbanising African context. ? It is a movable 'building' or 'watercraft' currently located in the aquatic community of Makoko in the lagoon heart of Africa's second most populous city - Lagos, Nigeria. It is a floating structure that adapts to the tidal changes and varying water levels, making it safe from flooding and storm surges. ? It is designed to use renewable energy, to recycle organic waste and to harvest rainwater. ?
Methods and processes:
The simple yet innovative structure adheres to ideal standards of sustainable development with its inclusive technologies for renewable energy, waste reduction, water and sewage treatment as well as the promotion of low-carbon transport. ? Furthermore a team of eight Makoko-based builders constructed it using eco-friendly, locally sourced bamboo and wood procured from a local sawmill. ?
A discussion of ONE example that reflects social responsibility
Construction began in September 2012 with floatation mock-ups and testing. Recycled empty plastic barrels found abundantly in Lagos were used for the building's buoyancy system, which consists of 16 wooden modules, each containing16 barrels. ? The modules were assembled on the water, creating the platform that provides buoyancy for the building and its users. ? Once this was assembled, construction of the A-frame followed and was completed by March 2013. Makoko Floating School is now in regular use by the community as a social, cultural and economic centre and will soon welcome its first pupils for use as a primary school. ?
Credit any other valid statements.
Q.5.1 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (20) |
Lower Order | Remember, Recall, Recognise, Name | 30% | 5.1.1 | 2 |
Understand, Explain, Describe, Classify | 5.1.2 | 4 | ||
Middle Order | Apply, Implement, Organise | 40% | 5.1.1 5.1.2 | 4 4 |
Higher Order | Analyse, Compare, Interpret | 30% | 5.1.2 | 3 |
Evaluate, Reflect, Judge | 5.1.2 | 2 | ||
Create, Synthesise, Justify | 5.1.2 | 1 |
OR
5.2 (OPTION 2) [20 marks]
5.2.1 (Allocate 10 marks: 2 marks per requirement)
Traditional beadwork was used as a method of colonial trade. ? It was also a means of expression, ? communication ? and storytelling. ? In the past, patterns and colours were woven into beadwork, symbolising feelings and ideas to lovers and friends ? e.g. Zulu Love Letters. Even though there is an influx of cultures in the present day, the traditional etiquette of beadwork communication is upheld by younger generations. ?
The value of traditional craft for any culture is to reconnect with ancestors, ? social and cultural practices ? and traditions, ? customs, ? heritage knowledge, ? historical background, ? identity, ? all in a desperate attempt to find out who we are, where we belong and where we are going. If we ignore our past, we have no way of finding our tomorrow. ? It is a reality that most South Africans idolise and adore Western American culture. ? If we do not value our traditional crafts, the South Africans may end up losing their cultural roots. ?
The function of most of the bead work is created by women living in the rural areas of South Africa. ? As human beings, they have always expressed themselves through personal decoration and that came as an expression to enhance physical appearance. ? Apart from enhancing physical appearance, beadwork could express superior status ? or may possibly possess magical properties to protect human from illness or hurtful forces. ?
The materials, methods and processes used by the beaders show the use of different kinds of materials to take beadwork to new levels by combining traditional beadwork skill with contemporary designs. ? To create jewellery and objects that delights the senses with their richness and colour. ? Seeds, stones, bits of bone, colourful glass beads and precious gemstones are used. ? The brightly coloured beads are creatively strung on cotton thread in diamond-shaped patterns in widths of three inches all around. ? The glass beads are usually arranged in blocks of five traditional colours (sky blue, grass green, red, black and yellow). ? 
A description of ONE example – isiZulu love letter
The beaded love letter is used by Zulu women to communicate with their men. ? This communication is coded in colours and geometric shapes of triangular shape and usually a maximum of seven colours. ? The three corners represent the father, mother and child. White usually represents spiritual love, purity and virginity. ?
Colour Coding refers to the use of various colours to convey meaning in a code. Colour coding assumes that in a given context various basic colours have a static meaning, literal or figurative. Regional styles speak largely to the outside. ?
- Name(s) of the craftsperson or indigenous cultural community that produced the craft: Zulu women in Hillcrest AIDS centre. ?
- Isishunka (seven colours) - white, light blue, dark green, pale yellow, pink, red and black.
- Isithembu (five colours) - light blue, grass green, bright yellow,red and black.
- Umzansi (four colours) – white, dark blue, grass green and red.
- Isinyolovane – a combination of any colours not consistent with other schemes.
Credit any other valid statements.
5.2.2 (Allocate 10 marks) 
- Name of designer/group and his/her/their design product/s
The Egg Chair by Studio Stirling. ? - A detailed description of how traditional technique/methods and material have been applied to contemporary design. Refer to specific examples to support your statements.
Studio Stirling makes beautiful handmade hanging chairs. ? The 'Egg Chair' makes use of durable steel material ? and is ideal for outside use. ? The 'Egg Chair' is handmade with unique individualism. ? The patterns are welded using a weaving technique to enhance the aesthetic and durable quality. ? The hanging chairs are the passion of Studio Stirling and their most popular models are the 'nest egg', 'recliner' and 'basket'. ? - Discuss the socio-cultural contribution of the design/s.
The founders of Studio Stirling consider the company as a program that has been designed to encourage collaboration between the designers, ? sharing common difficulties and solutions, mentorship and utilising new manufacturing processes and materials in a true interchange of skills, aesthetics and narratives. ? The company's headquarters are in South Africa, and it has branches worldwide. Studio Stirling is focused on identifying the specific areas of need of each company ? and is an immediate and business orientated initiative, repositioning the design companies in particular East, West and Southern Africa. ?
Q.5.2 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (20) |
Lower Order | Remember, Recall, Recognise, Name | 30% | 5.2.1 5.2.2 | 2 1 |
Understand, Explain, Describe, Classify | 5.2.1 5.2.2 | 2 1 | ||
Middle Order | Apply, Implement, Organise | 40% | 5.2.1 5.2.2 | 4 4 |
Higher Order | Analyse, Compare, Interpret | 30% | 5.2.2 | 2 |
Evaluate, Reflect | 5.2.1 | 2 | ||
Create, Synthesise, Justify | 5.2.2 | 2 |
QUESTION 6
6.1 [20 marks]
6.1.1 (Allocate 2 marks)
Sustainable designs reduce the consumption of non-renewable resources ? by the careful selection of materials that are bio-degradable and recyclable for design works. ?
Credit any other valid statements.
6.1.2 (Allocate 4 marks)
- Plastics
Some plastics are non-renewable, ? they account for the majority of waste that gets dumped in the rivers, sea, dams and landfills. Therefore the use of these plastics in design products helps minimise waste and the negative impact on the environment. ? - Tyres
Tyres are a non-renewable resource ? and the majority of people and the commercial transportation industries discard their old tyres in landfills. The use of these tyres as materials in the design of products helps minimise waste and the negative impact on the environment. ? - Wood
Wood is a durable bio-degradable/natural resource; ? the use of this material in design products has no negative impact on the environment. ? - Glass
Glass is a renewable material that can be melted to design new design products. ? The abundant wasted glass means that glass is readily available with our ever growing world population needs. ? - Paper
Used paper can be renewed and re-used in new products. ? The overly abundant unused paper enhances the sustainable nature of the product. ?
Credit any other valid statements.
6.2 Allocate 14 marks in total
(Allocate 7 marks per case study)
EXAMPLE OF A SOUTH AFRICAN DESIGNER:
(Allocate 1 mark to both the name of the designer and name of the product)
ONE CONTEMPORARY SOUTH AFRICAN DESIGNER WHOSE WORK EXPLORES SUSTAINABLE SOURCES/MATERIALS AND TRANSFORMS THEM INTO SIGNIFICANT DESIGN PRODUCTS. 

Erwin van der Weerd – Perfect Places architect ? (Allocate 1 mark)
Title and brief description of at least one example undertaken by the designer/design agency or studio (Allocate 3 marks)
The Hemp House built by Hemporium's Tony Budden and Duncan Parker, Cape Town South Africa. ?
The Hemp House is a two bedroom house, ? characteristically sharp-angled, sleek and minimalistic. ? The house was recently completed in Noordhoek, Cape Town, uses hempcrete, hemp insulation, ? hemp particle board for cupboards and wall claddings. ? Hemp carpeting is used for the flooring, ? hemp fabric for the curtains, upholstery, bed linen and lighting. ? Hemp insulation is used under the floor ? and hemp oil as a protective coat for timber furniture. ? The hemp aspect of the building, which accounts for up to 50% of the walls, was grown in a few months without the need for agro chemicals, ? and results in a breathable, natural, sustainable and carbon friendly building. ? The windows are gas-filled, ? they prevent heat leaking out of the closed windows with double action seal. ? The windows are complimented by an automated opening system attached to thermostats that regulate internal temperature by opening on the cooler/hotter side of the house depending on the time of the year. ? The kitchen is designed using a combination of recycled second-life store tops from Cannata and reclaimed Oregon pine. ? The bathrooms feature recycled second-life stone tops used on the bamboo vanities, imperviousness to water and aesthetic appeal. ? Cork flooring is used on the ground floor mainly because of the sustainability element (only the bark is harvested from the tree, causing no damage to the tree which regrows new bark). ? All lighting is energy-saving LEDs supplied by Earthpower. ? Appliances such as the refrigerator, washing machine, dishwasher and television are also energy saving compliant. ?
- Transformation of the sustainable material
The 'hemp house' is a project to showcase industrial hemp and its potential as an eco-construction material. ? The hemp house is a standing example of the viability of the replacing of traditional building materials with sustainable material. The house is also a reminder of the amazing environmental benefits which might be gained from more extensive integration of hemp into the construction industry. ? Hemp construction focuses on using the hemp stalks, which produces long strong hollow fibres that can be used to make insulation mats, ? while the woody part can be pressed into tree-free particle boards for use in cabinets and panelling, ? as well as hempcrete when mixed with a lime based binder. ? The aim of using hemp in construction is to move from an extractive method relying on mined and synthetic materials to a renewable method. ? - The impact of the design on the environment
Industrial Hemp refers to a non-narcotic cannabis cultivar that is used for a wide range of end products. Hemp has anti-bacterial and anti-allergenic properties ? with excellent thermal and sound insulation properties. ? As an organic fibre it allows the walls to breathe and helps purify the air. ? Hemp grows up to 4m tall in 4-5 months and is organic by nature. ? It can be used as a sustainable resource for paper, fuel, textiles, construction materials, bio-composites, nutrition, cosmetics and more. ? Currently it is strictly controlled due to its illicit cousin, marijuana/dagga, but over 40 countries are now growing it as part of a move back to a green sustainable economy. Hemp has a low carbon footprint and therefore has no negative impact on the environment. ?
EXAMPLE OF AN INTERNATIONAL DESIGNER
(Allocate 7 marks per case study – 1 mark for designer and design product) 
The bogobrush by John McDougall and Heather McDougall. ?
- Brief description of at least one example undertaken by the designer/design agency or studio
The bogobrush is a cylindrical shape biodegradable toothbrush. ? The nylon bristles of the brush are also 100% biodegradable. ? The design of the brush is simplistic. ? The cylindrical shape of the toothbrush allows it to fit perfectly in one's hand. ? The bogobrush bamboo handle replaces the rubber grips found on ordinary toothbrushes. ? - Transformation of the sustainable material
The toothbrush is constructed from the woody bamboo plant and waste plastics that were destined for the landfill. ? The plastics that are destined for the landfills are combined with plants from American farms to create the biodegradable handle. ? - The impact of the design on the environment
The bogobrush avoids contributing to the 450 million toothbrushes thrown away annually in the USA. ? The product has a low carbon footprint with no negative impact on the environment. ? Once aged beyond the recommended three months it can be thrown on a compost pile or just buried because of its biodegradable properties. ?
Credit any other valid statements.
Q.6 | COGNITIVE SKILLS | WEIGHTING | QUESTIONS | MARKS (20) |
Lower Order | Remember, Recall, Recognise, Name | 30% | 6.1.1 6.2 | 1 2 |
Understand, Explain, Describe, Classify | 6.1.1 6.1.2 | 1 2 | ||
Middle Order | Apply, Implement, Organise | 40% | 6.1.2 6.2 | 2 6 |
Higher Order | Analyse, Compare, Interpret | 30% | 6.1.2 | 2 |
Evaluate, Reflect, Judge | 6.2 | 2 | ||
Create, Synthesise, Justify | 6.2 | 2 |
TOTAL SECTION C: 40
GRAND TOTAL: 100
DANCE STUDIES GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
DANCE STUDIES
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
INSTRUCTIONS AND INFORMATION
- This question paper consists of TWO sections with TEN questions in total. Answer only EIGHT questions as follows:
- SECTION A: SAFE DANCE PRACTICE AND HEALTHCARE (40 marks)
- Answer FOUR of the five questions in this section.
- You have a choice between QUESTION 3 and QUESTION 4. If you answer both questions, only the FIRST answer will be marked.
- SECTION B: DANCE HISTORY AND LITERACY (60 marks)
- Answer FOUR of the five questions in this section.
- You have a choice between QUESTION 9 and QUESTION 10. If you answer both questions, only the FIRST answer will be marked.
- SECTION A: SAFE DANCE PRACTICE AND HEALTHCARE (40 marks)
- Number the answers correctly according to the numbering system used in this question paper.
- Read each question carefully and take note of what is required.
- NOTE: If you are requested to explain/elaborate/describe/analyse/ evaluate/compare, write your answer in full sentences and give as much information as possible. One-word answers will NOT be accepted.
- You may do rough planning in the ANSWER BOOK. Draw a line through any work that should NOT be marked.
- You will be assessed on your ability to:
- Use good English (write only in one language)
- Organise and communicate information clearly
- Use the specific format asked for in certain questions
- Use specialist dance terminology where appropriate
- Write neatly and legibly.
QUESTIONS
SECTION 1: SAFE DANCE PRACTICE AND HEALTH CARE
QUESTION 1: NUTRITION AND MENTAL HEALTH
1.1 Clearly explain what is meant by a balanced diet and how good nutrition could benefit a dancer's performance. (5)
1.2 Stress and tension can prevent a dancer from achieving his/her maximum potential in class. Describe TWO symptoms of stress and tension and how they could affect a dancer. (2)
1.3 Clearly describe THREE relaxation techniques you can use to reduce stress and tension. (3)
[10]
QUESTION 2: COMPONENTS OF FITNESS
There are FIVE components of fitness a dancer needs to perform optimally. Do NOT include nutrition or life style choices in the answer.
Give the following information:
- The name and a definition of each component (5)
- An explanation of how each component contributes to a dancer's performance (10)
[15]
NOTE: You have a choice between QUESTION 3 and QUESTION 4.
Answer only ONE of these questions.
QUESTION 3: MUSCLES AND ACTIONS
You have to tutor a Grade 10 dance class on some of the main leg muscles used in dance. Prepare the following information:
3.1 List FOUR important muscles/muscle groups and describe to the class where they are located. (4)
3.2 Choose any TWO muscles/muscle groups and write down the following:
- ONE anatomical action for each muscle/muscle group (2)
- An example of ONE dance movement that may be performed using the anatomical action given above (2)
[8]
OR
QUESTION 4: INJURIES AND TREATMENT
4.1 What is the difference between a sprain and a strain? (2)
4.2 Name FOUR of the main causes of a knee injury in the dance class. (4)
4.3 Explain TWO ways to protect your knees in the dance class to prevent possible knee injuries. (2)
[8]
QUESTION 5: POSTURE/SAFE STRETCHING
| A | B |
 | |
[Source: www.dancemagazine.com]
5.1 Study the photographs above. Indicate whether the postures in A and B are CORRECT or INCORRECT. Substantiate your answer, stating in EACH case, the relationship with safe dance practice. (3)
5.2 Many dance teachers, concerned parents and health professionals are struggling with what they see going on in the dance world, especially online.
 [Source: www.theballetblog.com] |  [Source: www.danceproject.ca] |
Refer to the statement and the pictures above and give your opinion and suggestions on safe stretching. (4) [7]
TOTAL SECTION A: 40
SECTION B: DANCE HISTORY AND LITERACY
QUESTION 6: COMMUNITY DANCE PROJECT AND CAREERS
The local government has requested you to organise the performances at a DANCE AND ARTS FESTIVAL they are funding in a poor community.
Prepare information for the local government that includes the following:
- At least FOUR aspects about the purpose of the dance and arts festival and the impact it could have on the community (4)
- Outline, in detail, THREE facilities and/or resources that will be needed for the performances (3)
- Name THREE arts production jobs that will be generated for the dance and arts festival and explain the function of each of these jobs (3)
[10]
QUESTION 7: FUNCTIONS OF DANCE IN SOCIETY AND DANCE FORMS
7.1 How can dance contribute to development in the categories below?
Choose only THREE categories and give an informative description of EACH area:
7.1.1 Education (2)
7.1.2 Social/Personal transformation (2)
7.1.3 Communication (2)
7.1.4 Religion (2)
7.1.5 Protest (2)
7.2 Compare and explain FOUR similarities and FOUR differences between the movement principles of African dance and the movement principles of ANY OTHER dance form you have studied.
Your answer must focus ONLY on the movement principles of the dance forms that you are discussing in your answer, African dance and another dance form. Name the other dance form in your answer. (8)
[14]
QUESTION 8: MUSIC OF A PRESCRIBED WORK
INTERNATIONAL CHOREOGRAPHERS | DANCE WORKS |
Alvin Ailey | Revelations |
Christopher Bruce | Ghost Dances |
George Balanchine | Apollo/Jewels (Emeralds, Rubies, Diamonds) |
Jiri Kylian | Wings of Wax/Stamping Ground |
Martha Graham | Lamentation/Errand into the Maze |
Matthew Bourne | Swan Lake/Cinderella |
Mats Ek | Giselle/Swan Lake/Carmen |
Pina Bausch | The Rite of Spring |
Rudi van Dantzig | Four Last Songs |
William Forsythe | In the Middle, Somewhat Elevated |
SOUTH AFRICAN CHOREOGRAPHERS | DANCE WORKS |
Alfred Hinkel | Cargo/I am Cinnamon/Rain in a Dead Man's Footprints/Bolero/Last Dance |
Carolyn Holden | Blood Wedding/Imagenes |
Dada Masilo | Swan Lake/Romeo and Juliet |
Gary Gordon | Bessie's Head |
Gregory Maqoma | Four Seasons/Skeleton Dry |
Mavis Becker | Flamenco de Africa |
Sylvia Glasser | Tranceformations |
Veronica Paeper | Orpheus in the Underworld/Carmen |
Vincent Mantsoe | Gula Matari |
Describe the music of ONE of the prescribed dance works you studied this year (listed above). Include the following:
8.1 Give the names of the dance work and choreographer that you chose.
8.2 Give the names of the composer, group or musicians. (1)
8.3 What is the genre or style of the music? (1)
8.4 Analyse how the music/accompaniment enhances this dance work. Give specific examples from the dance work. (4)
[6]
NOTE: You have a choice between QUESTION 9 and QUESTION 10. Answer only ONE of these questions.
QUESTION 9: CHOREOGRAPHER AND DANCE WORK
Select ONE of the dance works and choreographers from the list on page 7 and prepare an interview for a television talk show. You must set relevant, interesting questions and give factual answers about the choreographer and the dance work.
Give the names of the choreographer and dance work that you chose.
Your interview must include the following:
- An introduction and conclusion
- Influences, associations and collaborations
- Movement vocabulary and choreographic style used
- Symbolism
- Contribution to the dance profession
[30]
OR
QUESTION 10: SOUTH AFRICAN DANCE WORK AND CHOREOGRAPHER
Prepare a presentation for dance learners on the choreographer, Alfred Hinkel, and the dance work, Bolero/Last Dance.
Your presentation must include the following:
- An introduction and conclusion
- Influences, associations and collaborations
- Movement vocabulary and choreographic style used and how it was innovative
- Symbolism, your opinion/interpretation
- Contribution to dance in South Africa
[30]
TOTAL SECTION B: 60
GRAND TOTAL: 100
DANCE STUDIES GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
DANCE STUDIES
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
NOTE TO MARKERS:
Adhere strictly to this memorandum when marking. The standardisation process during memorandum discussions ensures that the memorandum covers most possible responses candidates could provide. Every marker must understand and apply it in the same way consistently. In some qualitative questions, exercise your professional and informed judgement.
Write short comments, giving reasons why a point was marked up or down if the memorandum does not give a clear guideline and you have to use your own discretion.
This question paper must be marked by experienced dance teachers/advisors/ officials as it requires specialist knowledge.
- In some questions, candidates have a choice. If candidates answered both questions, mark only the answers to the first question.
- Candidates may give a wide variety of answers, depending on what they covered in class.
- The rubrics guide the marking according to cognitive levels and levels of difficulty.
- Markers should NOT award full marks for an answer that is superficial and minimal.
- Read and evaluate the whole answer before allocating ticks and marks. One tick is one mark.
- Look for what the candidate knows, not what he/she does not know.
- Key words have been put in bold to guide marking.
MEMORANDUM
SECTION A: SAFE DANCE PRACTICE AND HEALTH CARE
QUESTION 1: NUTRITION AND MENTAL HEALTH
NOTE TO MARKER:
- Many possible answers may be provided by the candidates.
- If the candidate only gives one-word answers, give only half marks.
COGNITIVE LEVELS:
1.1 = 5 marks MEDIUM level
1.2 = 2 marks LOW level
1.3 = 3 marks LOW level
POSSIBLE ANSWERS:
1.1 Candidates could answer in many different ways to include both a balanced diet and the benefits.
An explanation of a balanced diet, e.g.
A balanced diet includes all the main food groups to ensure the body works at its best, for example:
Complex carbohydrates:
- They elicit the most energy and should constitute the bulk of the diet, as they will sustain you through many hours of rehearsals and performances.
- They are digested slower, providing a slow and stable supply of energy.
Proteins:
- Build and maintain the tissues of your body.
- They are important for muscle repair and growth.
Dairy products:
- Are important to build calcium in the bones and without sufficient calcium bones become brittle and can easily be broken or fractured.
Fruit and vegetables
- Through eating vegetables and fruit the body is provided with the necessary vitamins and minerals which are required for overall well-being.
- Vitamin supplements may be used if the body receives too little from the food that is eaten, so that the dancer is not prone to regular illnesses and off work or missing classes.
Fat:
- A small amount is necessary for organs to function optimally, such as the heart and brain.
Any other suitable answers.
Benefits of good nutrition to a dancer's performance could include:
- Increased energy levels
- Increased mental alertness
- Increased fitness levels
- Maintain an ideal weight
- Recover from illness/injuries quicker
- Ability to handle higher levels of stress – emotional well-being
- Increased strength – muscle mass
- Positive attitude towards training and performing (5)
1.2 Candidate may provide any two symptoms of stress and tension:
- Fatigue will set in impairing a dancer's judgment in class/ rehearsals and performance.
- Eating related disorders from a poor diet could severely impair a dancer's future career.
- Physical - muscle tension/ stiffness, cramps, aches and pains, frequent colds, rapid heartbeats.
- Mental - moody, irritable, unhappy; will prevent the dancers from interacting with/ working successfully with others in the dance class.
- Lack of sleep or sleeping too much – this could lead to lack of concentration in the dance class which could lead to injuries.
- Loss of appetite or eating too much – this could affect the dancer's self image and lead to lack of confidence.
Any other suitable answers (2)
1.3 Candidate must clearly describe any THREE relaxation techniques e.g.:
- Create a safe space for yourself where you can apply relaxation techniques such as imagery/ breathing etc. and calm your mind.
- Cool down techniques to release tension in muscles such as slow stretching.
- Candidates could supply a specific technique e.g. yoga or meditation.
Any other suitable answers. (3)
[10]
QUESTION 2: COMPONENTS OF FITNESS
COGNITIVE LEVELS:
5 marks = LOW level for the name and definition
10 marks = MEDIUM level for explaining
POSSIBLE ANSWERS:
Allocate ½ a mark if candidates provide only the name with no definition.
- Core stability: the strength in the centre of the body, abdomen and back.
- Strength: the ability of a muscle to exert force against gravity.
- Flexibility: a wide range of movement possible in the joints.
- Endurance: the staying power of the body to perform over longer periods of time.
- Neuromuscular skills: the ability of the brain to send messages to the body with an instant reaction time. (5)
Explaining how each component contributes to a dancer's performance.
Many of the benefits apply across components.
Evaluate the whole answer.
Do not award marks for repetitive answers in this bullet.
Ten clear facts = 10 marks.
Strength:
- Stronger muscles mean more complex movements can be performed and positions held, i.e. the muscles can resist giving into gravity.
- Can perform lifts and jump higher.
Flexibility:
- Adds grace and ease to movements.
- Dance will look effortless.
- Dancers will have a wider range of movement.
Core stability:
- Can control movements.
- Makes balancing easier.
- Maintains good posture.
- Can shift body weight quickly etc.
Neuromuscular skills:
- Can move quickly – more agile.
- Improved co-ordination.
- Better musicality.
- Improved kinaesthetic awareness, spatial awareness, etc.
Endurance:
- You won't get out of breath.
- You will be able to maintain concentration without having to worry how you are going to finish the class.
- Your arms, legs and body won't feel heavy and fatigued, etc.
Any other suitable answers (10)
[15]
NOTE: The learners have a choice between QUESTION 3 and QUESTION 4.
Mark only the first answer if both questions have been answered.
QUESTION 3: MUSCLES AND ACTIONS
COGNITIVE LEVELS:
3.1 = 4 marks = LOW level – naming muscles/groups and describing where they are found
3.2 = 4 marks = MEDIUM level =
2 marks for anatomical actions
2 marks for explaining one dance movement using the anatomical action
POSSIBLE ANSWERS:
3.1 Allocate FOUR marks for naming and describing where the FOUR muscles/groups are found. Award ½ a mark for naming only.
- Quadriceps:
This muscle group is found on the front of the thigh. - Hamstrings:
This muscle group is found at the back of the thigh. - Adductors:
This muscle group is found on the inside of the thigh. - Gastrocnemius:
This muscle is found at the back of the lower leg.
Any other muscle/muscle group in the leg, such as abductors, hip rotators and anterior lower leg muscles. (4)
3.2 Allocate TWO marks for providing two anatomical actions and TWO marks for explaining ONE dance movement for each of the anatomical actions.
- Quadriceps:
Extension of the knee – stretch the knee - Rectus femoris
Flexion – throwing the leg up high to the front of the body in a kick. - Hamstrings:
Extension – lifting the leg behind the body. - Adductors:
Adduction – it is a group of muscles that turn out the legs or move the legs away from the midline/centre (outward rotation). - Gastrocnemius:
Plantar flexion – it is responsible for lifting the heels in rises, pointing the feet and helps to push off the floor in jumps and flexes the knee.
Any other muscle/muscle group in the leg. (4)
[8]
OR
QUESTION 4: INJURIES AND TREATMENT
COGNITIVE LEVELS:
4.1 = 2 marks = MEDIUM level
4.2 = 4 marks = LOW level
4.3 = 2 marks = MEDIUM level
POSSIBLE ANSWERS:
4.1 Difference:
- Sprain = an injury to a ligament.
- Strain = an injury to a muscle or tendon. (2)
4.2 Possible answers related to causes of knee injuries:
- Poor alignment of the knee
- Forcing turnout of leg
- Incorrect landing from a jump
- Dancing on incorrect floors – not sprung wood
- Lack of strength to control movements
- Poor technique
- Poor conditioning
- Not warming up correctly
- Falls, as in an accident or in the choreography
- Lack of flexibility
- Any other suitable answer related to knee injuries. (4)
4.3 Possible answers on how to protect your knees in the dance class:
- Apply safe dance practice, like keeping your knees over your middle toe when you bend your knees or land from a jump.
- Do not place stress on the ligaments by moving the joint beyond its normal range and movement direction.
- The knees should always bend before a jump, land through the foot and end in a knee bend/ demi plié. This landing will prevent the knees and ankles from jarring and causing serious damage to the knees and ankles.
- Strengthening the surrounding muscles of the joint, e.g. the hamstrings and the quadriceps muscle groups, located at the back and front of the knee, stabilises the knee joint. Strengthening these muscles has a protective effect on the knee, and can decrease the stress on the knee joint during exercise. (2)
[8]
QUESTION 5: POSTURE AND SAFE STRETCHING
COGNITIVE LEVELS:
5.1 = 3 marks HIGH level
5.2 = 4 mark HIGH level
POSSIBLE ANSWERS:
5.1 Referring to the photographs. Indicate correct and incorrect postures.
- PHOTOGRAPH A is an example of an incorrect posture, where the dancer's back is overarched; the pelvis is not well aligned which could result in serious back problems, such as strain in the lumbar spine, stiff neck as the head is out of alignment (chin thrust forwards).
- The dancer's core muscles are not used, which will prevent the dancer from balancing and controlling the body, limbs during movements.
- Any other suitable answers.
- PHOTOGRAPH B is an example of good dance posture and is the correct way to hold the posture while dancing.
- The head is up, the neck is long with core stability and the joints lined up.
- Dancer B understands how the different parts of the body work in relation to one another and this will enable the dancer to be able to balance and have control of all movements. This will also ensure ease of movement during all activities. (3)
5.2 Referring to the pictures: Areas that could be included in the answer for own opinion and suggestions on safe stretching:
- Dancers should be aware that there are different types of stretching that you can use to become supple.
- Both pictures show dangerous stretching methods which should be avoided to prevent injuring your muscles and ligaments.
- Stretching should not be painful – it can be difficult, but should not elicit pain.
- Never force your body into a stretch or allow somebody else to force you into a stretch, as this is dangerous and will cause injury.
- Breathing is important to use when stretching as this will help to ease your body into the stretch.
- A dancer must always be aware of his/her body's limitations and work within that framework when doing stretching or strengthening exercises.
Any other suitable answers/suggestions. (4)
[7]
TOTAL SECTION A: 40
SECTION B: DANCE HISTORY AND LITERACY
QUESTION 6: COMMUNITY DANCE PROJECT AND CAREERS
COGNITIVE LEVELS:
- Bullet 1: MEDIUM level
- Bullet 2: LOW level
- Bullet 3: LOW level
Many possible answers will be provided. Answers must link to the performances at the dance and arts festival. Look at the whole answer before awarding marks.
POSSIBLE ANSWERS:
FOUR aspects about the purpose and the impact it may have on the community, e.g.:
- To identify artists and talent in the community – nurture this further
- To make arts accessible in the community
- To provide exposure for local and professional artists
- To create jobs in the community
- To give youngsters a goal to work towards
- To bring people together from different communities
- To inspire young artists
- To share skills and develop new talent/ existing talent
- To provide a platform for the arts
- To promote entrepreneurship and commercial activity in the community
Any other suitable answer (4)
THREE facilities and resources needed for the performances, e.g.:
- Performance space indoor/outdoor amphitheatre, e.g.:
- Chairs/Seating for the audience
- Stage with a suitable/sprung wooden floor
- Suitable size for the type of performances
- Dressing rooms for the performers
- Sound equipment to include:
- Amplifiers
- Speakers with enough volume
- Microphones
- Publicity materials to include:
- Posters/Flyers for advertising
- Programme of events for the festival
- Announcer for the festival
- Sponsors
Any other suitable answers. (3)
THREE arts production jobs that will be created for the dance and arts festival and explanation of the function of each. One-word answers must NOT be awarded full marks. Do NOT award marks for jobs not related to arts production, e.g.:
- Organiser(s)/Manager/Event organiser/Project manager who will plan all the events and order of the festival.
- Publicist to advertise the festival and ensure full participation of the community.
- Choreographers/Directors for the various dance pieces/arts to be performed or exhibited.
- Teachers/Facilitators to help run arts workshops for the children.
- Sound technician who will be in charge of playing the music/microphones/ announcements, etc.
- Dancers/Actors/Musicians, etc. who will perform for the community.
Any other suitable art production jobs. (3)
[10]
MARKING RUBRIC
DESCRIPTOR | MARK | THE CANDIDATE |
Outstanding | 9–10 |
|
Adequate | 6–8 |
|
Moderate | 3–5 |
|
Not Achieved | 0–2 |
|
QUESTION 7: FUNCTIONS OF DANCE IN SOCIETY AND DANCE FORMS
COGNITIVE LEVELS:
7.1 = 6 marks LOW level
7.2 = 8 marks HIGH level – comparing
7.1 Mark only the FIRST THREE if more categories are provided. An informative description is required for each answer.
7.2 Evaluate the whole answer before awarding marks. HIGH level as candidate is asked to compare and explain in full sentences FOUR similarities and FOUR differences between African dance principles and another dance form. Do not award marks if candidates include other areas for comparison, such as costumes and props.
7.1
7.1.1 Education:
- Dance can be used to pass on traditions/history of a community.
- It can be used to educate communities on social issues.
- It can prepare people for careers.
- It can teach life skills, such as discipline and team work.
Any other relevant answer. (2)
7.1.2 Social/Personal transformation:
- Dance is used in many ceremonies, e.g. of coming of age – move from being a child to adulthood. Weddings – move from being single to being married, etc.
- Dance is used in rituals for healing – moving from illness to health.
- Many dancers experience a sense of personal transformation through dance, e.g. a sense of purpose, improved life skills and increased awareness of others.
- Dance is used to build social skills through teamwork and trust exercises.
Any other relevant answers. (2)
7.1.3 Communication:
- To put across ideas and thoughts. To inform without using words – dance is a universal language.
- To show and express emotions non-verbally.
Any other relevant answer. (2)
7.1.4 Religion:
- Dance is used in many spiritual ceremonies to enhance the meaning/message.
- Dance used in religious customs or charismatic church services can be linked to transformation.
Any other relevant answer. (2)
7.1.5 Protest:
- Dance is used to make political statements without using words.
- Dance is used to demonstrate – toyi-toyi.
- Any other relevant answers. (2)
7.2 Many possible dance forms will be provided by the candidates. African dance must be included as one of the dance forms.
ONLY movement principles must be included in the answer.
Bullets are used to aid marking.
CONTEMPORARY VS. AFRICAN DANCE
Differences could be:
- African dance movements are traditional and often do not change.
Contemporary dance movements are often created through improvisation and differ from one choreographer to another. - African dance and music are not separate from each other. The dancers incorporate singing/body percussion/ululating, etc. into their movements.
Contemporary dance usually chooses pre-recorded music that will enhance the intent/story of the dance work and choreograph movements to fit the music and may work without music. - African dance imitates movements literally found in the natural world.
Contemporary dance adapts natural movements through abstraction. - Contemporary dance often involves lifting/counterbalance between dancers.
African dance does not involve lifting of partners but rather focuses on line/circle formations. - African dance is rhythmic.
Contemporary dance is more visual. (4)
Any other suitable answers.
Similarities could be:
- Both dance forms complement gravity in their movements/giving into/ dance towards the ground.
- Both dance forms are performed mostly with bare feet.
- Both dance forms use everyday movements/gestures.
- Both dance forms use large jumping and leaping movements defying gravity.
Any other suitable answers. (4)
[14]
MARKING RUBRIC 7.2
DESCRIPTOR | MARK | THE CANDIDATE |
Outstanding | 7–8 | Compares and explains, in well written full sentences, FOUR differences and FOUR similarities between African dance principles and the dance principles of one other dance form. Shows in-depth understanding of the movement principles of both dance forms. |
Adequate | 5–6 | Compares and explains, in full sentences, FOUR differences and FOUR similarities between African dance principles and the dance principles of one other dance form. |
Moderate | 3–4 | Comparison basic/limited in many aspects of FOUR differences and FOUR similarities between African dance principles and the dance principles of one other dance form. |
Not Achieved | 0–2 | Cannot compare/minimal/ no knowledge of African dance principles and the dance principles of one other dance form. |
QUESTION 8: MUSIC OF A PRESCRIBED WORK
COGNITIVE LEVELS:
8.2 = 1 mark LOW level
8.3 = 1 mark LOW level
8.4 = 4 marks MEDIUM level
POSSIBLE ANSWERS:
8.1 Ghost Dances Christopher Bruce
8.2 Inti-Illimani (1)
8.3 Traditional Chilean folk music (1)
8.4 Candidates must analyse how the music enhances the work. One-word answers are not acceptable.
Answers could include:
- Wind sounds in the beginning set an eerie atmosphere, symbolise being in the cave, make the setting more real, etc.
- Folk music using traditional South American instruments enhances the folk style of movements and helps to tell the story.
- The songs are sad and haunting telling of the suffering of the people and this is portrayed through their movements, e.g. the woman in the red dress.
- Some of the songs and music are upbeat and fast creating the atmosphere of what life must have been like before the war, e.g. Section 2 with the 3 men and 3 women.
- At the moment of death there is silence which adds to the atmosphere and sadness of the moment.
Any other suitable answer. (4)
[6]
NOTE: The candidate has a choice between QUESTION 9 and QUESTION 10. Mark ONLY the first answer if both questions have been answered.
QUESTION 9: CHOREOGRAPHER AND DANCE WORK
COGNITIVE LEVELS:
2 marks = LOW level – introduction/ conclusion
20 marks = MEDIUM level – influences/collaborations/associations/movement vocabulary/ choreographic style/contribution to dance 8 marks = HIGH level – symbolism/your opinion/interpretation
Use professional judgment and an in-depth knowledge of the choreographer and the dance work when marking. Bullets used to aid marking.
MARKING RUBRIC:
DESCRIPTOR | MARK | THE CANDIDATE |
Outstanding | 24-30 |
|
Meritorious | 21–23 |
|
Substantial | 18–20 |
|
Adequate | 15–17 |
|
Moderate | 12–14 |
|
Elementary | 10–11 |
|
Not Achieved | 0–9 |
|
QUESTION 10: SOUTH AFRICAN DANCE WORK AND CHOREOGRAPHER
COGNITIVE LEVELS:
- 2 marks = MEDIUM level – introduction/conclusion/presentation 20 marks = MEDIUM level – influences/collaborations/associations/movement vocabulary/choreographic style/contribution to dance 8 marks = HIGH level – symbolism, opinion/interpretation
- Use professional judgment and an in-depth knowledge of the choreographer and the dance work when marking.
- Bullets used to aid marking.
Candidates must prepare a presentation for dance learners about the choreographer, Alfred Hinkel, and the dance work, Bolero/Last dance. The presentation may be bullets, a mind map or in essay format and should include the following:
An introduction and conclusion.
Influences, associations, collaborations.
Possible areas that could be included:
- Hinkel grew up in a conservative family in Namaqualand.
- He started dancing at the age of ten, although his father was against him dancing.
- In the early 1970s he continued his training at the UCT School of Dance for a short time, thereafter returning to his home in Namaqualand.
- It was his daily experience of teaching in the 'coloured' communities (without proper facilities) that laid the foundation for a truly original and resourceful approach to dance teaching and choreography.
- Hinkel met John Linden and Dawn Langdown in Okiep, Namaqualand, two people with whom he would consistently collaborate over the years to come.
- Together they formed the Namaqualand Dansgeselskap.
- In 1981 he joined Jazzart Dance Theatre as a dancer and eventually took over as the director.
- Through the turbulent times of the state of emergency he became increasingly politicised which was reflected in his work.
- Exposure to working through improvisation during the Abamanyani process influenced the way he began to work and he has developed a unique way of teaching and choreographing, drawing from the essence of the dancers.
Any other factual answers.
Movement vocabulary and choreographic style used and how it was innovative.
- Bolero was a novelty in its time. Hinkel's work featured elements seldom (or never) seen on stage before such as:
- African dance was staged as performance art.
- Previously, African dance had been viewed as a quaint tourist attraction.
- The staging of the earlier versions of Bolero was vital in asserting a recognised place for African contemporary dance in the world of South African performance art.
- African dance was set to classical music
- Gumboots were worn by women and in particular, white women. One needs to appreciate that gumboot dancing arose from, 'a working class people, mostly miners and dock workers', and that it was not a practice performed by women, let alone white women.
- Thus, when the female cast of Bolero, marched proudly onto stage, they crossed a cultural and societal threshold.
- Gumboots were used in an 'avant-garde' way.
- Traditionally performed with a bent back, Hinkel demonstrated how an established technique could be manipulated for creative purposes when his dancers were seen performing their own, upright version of gumboot dancing.
- The contact work featured in Bolero was very innovative for its time.
- The traditional roles of men and women were disregarded.
- In Bolero, men lift men, women lift women, women lift men and so on.
- The traditional roles of the male and female were turned upside down when Hinkel's piece subversively suggested that women were entitled and able to initiate action and assume leadership and that men could feel weak and vulnerable.
- Bolero made bold political assertions.
- With each version the choreography has been influenced by the participants, each bringing their uniqueness to the interpretation as Hinkel has always used improvisation when creating dance works.
- He also fused different dance forms such as contemporary and African dance as well as Indian and contemporary dance.
Any other suitable answers.
(Note there could be an overlap between movement vocabulary and symbolism)
Symbolism/opinion/interpretation
- Bolero has been staged in diverse forms to fulfill numerous purposes. In the earlier versions of Bolero, Hinkel intended to make symbolic statements through dance on issues that were not meant to be talked about (this almost became one of Jazzart's policies) about politics, abuse, sexuality etc.
- Every performance of the work symbolised a shift in the attitude of the people and the country from apartheid to post-apartheid. Initially, it served to comment on politics, then for celebration (it was performed at the inauguration of Nelson Mandela) and also as incentive for collaboration between classical and contemporary dance companies as the giver of hope.
- Bolero is a work that has traced a fairly political path and has continually transformed through the process of being reworked on each of the several occasions that it has been staged to create new meaning.
- The original version symbolised 'overcoming prejudice', and focused specifically on the Immorality Act – arguably the most controversial of the legislative acts of the South African Apartheid government which attempted to forbid intermixing of couples of different races.
- The costumes were used to make statements such as non-gender specific costumes worn symbolising gender discrimination, leather and chiffon together symbolising the strength and softness of women, etc.
- Any other suitable answers, opinions/interpretations.
Contribution to dance in South Africa.
- Hinkel works predominantly with untrained dancers and develops their talent through training methods developed from working in underprivileged areas.
- He developed his own style of training and developed a method that he would use over the next 30 years to train his dancers. This style has now been adopted and developed by many dancers, choreographers in their own way.
- Hinkel combines a mixture of styles as well – contemporary, African, Indian as well as classical elements of dance which has also influenced ways of choreographing in this country.
- Used dance to make social commentary especially to do with sexism, racism and other forms of discrimination and abuse of power.
- He developed and popularised improvisation as a means of creating new material for choreography.
- Is outspoken about injustices.
- He mentored many fledgling dance companies.
- Supported schools with artists in residence and lecture demonstrations.
- He trained many dancers through a training programme run by Jazzart who have become the next generation of master teachers and choreographers.
[30]
TOTAL SECTION B: 60
GRAND TOTAL: 100
CONSUMER STUDIES GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
CONSUMER STUDIES
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
MEMORANDUM
QUESTION 1
1.1
1.1.1 C✔ Understanding, easy (Focus, p.104; Successful, p.126) (1)
1.1.2 D✔ Understanding, easy (Focus, p.75; Successful, p.85) (1)
1.1.3 C✓ Understanding, easy (Focus, p.77; Successful, p.91) (1)
1.1.4 A✓ Understanding, easy (Focus, p.77; Successful, p.91) (1)
1.1.5 A✓ Understanding, easy (Focus, p.79; Successful, p.93) (1)
1.1.6 C✔ Understanding, moderate (Focus, p.49; Successful, p.54) (1)
1.1.7 D✔ Remembering, easy (Focus, p.61; Successful, p.67) (1)
1.1.8 A✔ Remembering, easy (Focus, p.117; Successful, p.137) (1)
1.1.9 B✔ Remembering, easy (Focus, p.128; Successful, p.146) (1)
1.1.10 B✔ Remembering, easy (Focus, p.61; Successful, p.67) (1)
1.1.11 A✔ Remembering, easy (Focus, p.148; Successful, p.162) (1)
1.1.12 B✔ Remembering, easy (Focus, p.134; Successful, p.155) (1)
1.1.13 D✔ Remembering, easy (Focus, p.122; Successful, p.140) (1)
1.1.14 D✔ Remembering, easy (Focus, p.64; Successful, p.72) (1)
1.1.15 A✔ Understanding, easy(Focus, p.40; Successful, p.42) (1)
1.1.16 D✔ Understanding, moderate (Focus, p.13; Successful, p.19-20) (1)
1.1.17 C✔ Understanding, moderate (Focus, p.17; Successful, p.22) (1)
1.1.18 B✔ Understanding, moderate (Focus, p.168; Successful, p.185) (1)
1.1.19 C✔ Understanding, difficult (Focus, p.166;Successful, p.183) (1)
1.1.20 B✓ Analysing, difficult (Focus, p.167-168; Successful, p.185) (1)
1.2
1.2.1 emulsifiers✓ (Focus, p.93; Successful, p.113) (1)
1.2.2 stabilisers✓ (Focus, p.93 ; Successful, p.113) (1)
1.2.3 bleaches✓ (Focus, p.94 ; Successful, p. 113) (1)
Remembering, easy
1.3
D✔
E✔
F✔
H✓ (in any sequence) (4)
Remembering, moderate (Focus, page 136–137; Successful, page 157)
1.4
1.4.1 B✔ (Focus, p.7; Successful, p.12 and 35) (1)
1.4.2 A✔ (Focus, p.37; Successful, p.36) (1)
1.4.3 G✔ (Focus, p.36-37; Successful, p.35–37) (1)
1.4.4 C✔ (Focus, p.40; Successful, p.39) (1)
Understanding, moderate
1.5
1.5.1 D✓ (Focus, p.158; Successful, p.176) (1)
1.5.2 B✓ (Focus, p.159; Successful, p.177) (1)
1.5.3 C✓ (Focus, p.162; Successful, p.178) (1)
1.5.4 E✓ (Focus, p.161; Successful, p.177–178) (1)
Understanding, moderate
1.6
A✔
D✔
F✔
G✓
H✓ (in any sequence) (5)
Analysing, moderate (Focus, page 49, 51, 57-59; Successful, page 50, 51, 59–65 and CAPS (Grade 11)
[40]
QUESTION 2: THE CONSUMER
2.1
2.1.1 South African Revenue Service/SARS✓ (1)
Remembering, easy (Focus, page 163; Successful, page 181)
2.1.2 Pay-as-you-earn/PAYE✓ (1)
Remembering, easy (Focus, page 163; Successful, page 181)
2.1.3 (4)
Non-provisional tax | Provisional tax | |
Regularity/ Type of income earned | Employed by an employer/full-time employed/regular monthly income/fixed monthly income/earning a salary✓ (1) | Income is not fixed/irregular income/people with income other than salaries✓ (1) |
How often the tax is paid | Every month/ monthly✓ (1) | Twice a year✓ (1) |
Understanding, moderate (Focus, page 163; Successful, page 181)
NOTE: Deduct one mark if not answered in table format.
2.2
- An exemption clause is a clause included in contracts that exonerates (clears) a party from any liability✓ should he/she fail to honour the agreement/when the agreed product or service does not serve the purpose for which it was acquired.✓ (2)
Understanding, easy (Focus, page 156; Successful, page 173)
2.3
2.3.1
- Kettle✓
- Basic light✓
- Heating of water✓
- Ironing✓
- Small (black and white) television✓ (Any 2) (2)
Remembering, easy (Focus, page 183; Successful, page 203)
2.3.2
- Set the geyser temperature to 60 °C/reduce the geyser temperature.✓
- Install a geyser timer that can be set to turn on the geyser early in the morning and on again in the evening.✓
- Insulate the geyser/use a geyser blanket and outlet pipes to prevent heat loss.✓
- Use a low-flow shower head as they use 40 per cent less hot water.✓
- Install a solar energy/solar water-heating unit with a geyser to heat water as 25 per cent or more can be saved on the electricity bill.✓ (Any 2) (2)
Understanding, moderate (Focus, page 174; Successful, page 192)
2.4
- Inflation: Inflation increases the price of goods and services therefore consumers will spend more on food.✔
- Rising petrol prices: When the petrol price increases, transporting food to the point of sale will increase✓ therefore food prices will increase even more as the consumer eventually pays for the increase of the petrol price.✔
- Food bought on credit: If food is bought on credit, as well as increased interest rates may increase the food price even more.✔
- Depreciation of the rand: Imported foods will cost more.✓ (Any 4) (4)
Applying, difficult (Successful, page182-185; Focus, page 164-168)
2.5
- It is very likely that this is a fake e-mail/phishing/scam/ identity theft.✓
- It is very unlikely that any financial institution will offer an interest rate as low as 4,00%✓ as it is lower than the repo rate and the institution will make no money.✓
- This deal looks too good to be true, so it is possibly too good to be true/not true.✓ (Maximum 3)
- A consumer should not give/email any personal details to Elite Loans.✓
- It is best to delete this e-mail.✓ (Minimum 1) (4)
Analysing, moderate (Focus, page 159; Successful, page 177)
[20]
QUESTION 3: FOOD AND NUTRITION
3.1
- Antioxidants preserve the quality of food/lengthen the shelf life✔ of food.
- Prevent rancidity✔and unpleasant taste and smell✔ in margarine/cooking oil/biscuits/potato chips/soup mixtures.
- Preserve the colour of fresh cut fruit and vegetables/delay enzymatic browning/discolouration in fruit and vegetables/fruit juice/soft drinks/ canned vegetables/frozen fruit.✔ (Any 3) (3)
Remembering, moderate (Focus, page 34; Successful, page 114)
3.2
- Drink water only from safe water supplies that are regularly chlorinated.✓
- Boil water✓ for 10 to 15 minutes if you are not sure that it is safe.
- Don't swim in infected water.✓
- Don't wash fruit/vegetables in infected water.✓ (Any 2) (2)
Remembering, easy (Focus, page 90; Successful, page 107-108)
3.3
- Food irradiation destroys micro-organisms/pathogenic bacteria/other harmful organisms✓ in order to prevent food-borne diseases/make food safer to eat.✓
- It destroys or deactivates organisms that cause food spoilage.✓ In this way the shelf life of fruit and vegetables is extended/ can be stored for longer.✓
- Irradiation delays the sprouting of onion/garlic/potatoes/ripening of fruit,✓ so it reduces losses from damage during transportation/ storage.✓ In this way, the shelf life of the fruit and vegetables is extended.✓
- It destroys insects in or on tropical fruit that is imported/exported.✓ In this way, the shelf life of the fruit is extended.✓ (Any 2 x 2) (4)
Understanding, moderate (Focus, page 105; Successful, page 127)
3.4
3.4.1
- Diabetes is a chronic disease in which the blood-glucose level is abnormally high✓ because the body cannot control it properly.✓ It occurs when the beta cells in the pancreas do not produce any insulin✓ or do not produce enough insulin✓, or when the body does not use insulin effectively.✓
OR - Diabetes develops when the body does not make enough insulin✓ or is unable to use the insulin✓ it makes. Insulin is needed to turn sugar into energy.✓ Without insulin sugar builds up in the blood/ high blood sugar levels develop.✓ (Any 3) (3)
Remembering, easy (Focus, page 72-73; Successful, page 80)
- Diabetes is a chronic disease in which the blood-glucose level is abnormally high✓ because the body cannot control it properly.✓ It occurs when the beta cells in the pancreas do not produce any insulin✓ or do not produce enough insulin✓, or when the body does not use insulin effectively.✓
3.4.2
- There is a link between type 2 diabetes and lifestyle.✓
- The onset of type 2 diabetes may be prevented or delayed by following a healthy diet.✓
- Maintaining a normal body weight✓as obesity/overweight increases the risk of coronary heart disease and diabetes. ✓
- Having an active lifestyle/regular exercise✓ helps the body to use insulin more effectively,✓ which controls blood glucose levels.✓ (Any 5) (5)
Understanding, moderate (Focus, page 73; Successful, page 82)
3.5
- Fresh fruit and vegetables contain vitamin C✓which promotes/enhances the absorption of iron.✓
- Iron is found in green leafy vegetables will assist in the formation of haemoglobin/red blood cells.✓ (Any 2) (2)
Understanding, moderate (Focus, page 76-77; Successful, page 91)
3.6
3.6.1
- Hypertension is caused when the blood pressure against the walls of the arteries✓ remains high for a long time.✓
OR - Hypertension develops if the walls of the larger arteries lose their natural elasticity✓ and become rigid,✓ and the smaller blood vessels become narrower due to blood pressure that remains high for a long time.✓
OR - The pressure of blood that flows in the arteries✓ is measured at a high and a low point.✓ If blood pressure is too high/hypertension puts you at risk✓ of a heart attack/stroke/kidney damage/eye damage. (Any 2) (2)
Remembering, moderate (Focus, page 77; Successful, page 86)
- Hypertension is caused when the blood pressure against the walls of the arteries✓ remains high for a long time.✓
3.6.2
- Saul must use herbs/spices to flavour his food✓ instead of salt.
- Reduce the intake of processed foods/snacks/smoked meat/bacon/biltong/potato chips/junk foods/salted nuts/peanuts/salted popcorn/salty cracks/pizza as it contains hidden salt.✓
- Avoid/limit food that has salt/sodium/sodium chloride/mono sodium glutamate (MSG) on the list of ingredients.✓
- Avoid/limit salty food products/products high in salt which is more than 600 mg/1,5 g salt per 100 g.✓
- Do not consume more than 5 g/1 teaspoon salt per day.✓
- Eat food products low in salt/less than 120 mg/0,3 g salt per 100 g.✓
- Limit the amount of salt when cooking. ✓
- Avoid sprinkling extra salt on cooked food.✓ (Any 5) (5)
Applying, moderate (Focus, page 77; Successful, page 87-88)
3.7 (4)
CRITERIA | GUIDELINES TO PREVENT OBESITY | HEALTHIER ALTERNATIVE |
COOKING METHODS USED |
|
|
CARBOHYDRATE INTAKE |
|
|
Understanding, moderate (Focus, page 98; Successful, page 83)
NOTE: One mark must be deducted if not in table format.
3.8
ONE BREAD TYPE | ONE SPREAD | ONE PROTEIN FILLING | TWO ACCOMPANIMENTS |
Wholewheat/ brown bread✓
| 'Lite' margarine✓
| Smoked chicken/ Tuna mayonnaise✓
| Tomato/ Cucumber/ Low fat cheese/ Lettuce
|
NOTE: One mark for each choice and One mark for a reason. (10)
Analysing, difficult (Focus, page 73-75; Successful, page 83-85)
[40]
QUESTION 4: CLOTHING
4.1
- They pay fair wages.✓
- They provide good working conditions.✓
- They provide decent work hours.✓
- They do not use child labour.✓
- They comply with civil labour laws and safety laws.✓
- They support environmental sustainability.✓ (Any 3) (3)
Remembering, easy (Focus, page 61; Successful, page 69)
4.2
- The invention of new textiles/fabrics✓ leads to fashion change.
- Biotechnology/nanotechnology opened up a range of fabrics with special characteristics for specific purposes,✓ such as sportswear.
- Computerised pattern-design methods/improved knitting and sewing machines✓ lead to fashion change.
- Easy communication on fashion via television and social media/Internet/ cellphone/Facebook/twitter✓ leads to fashion change. (Any 2) (2)
Remembering, moderate (Focus, page 51; Successful, page 54)
4.3
First impressions are often lasting impressions.✓ People will judge you on your physical appearance✓ even before they speak to you.✓ A person who is dressed appropriately/smartly✓ gives the impression that he/she is confident,✓ ready to learn✓ and ready for doing good work for the company.✓ Your goal with first impressions should be to project a professional/competent image.✓ (Any 3) (3)
Understanding, easy (Focus, page 53; Successful, page 57)
NOTE: Deduct ONE mark if the answer is not written in a paragraph.
4.4
4.4.1
- Fashion cycles will be shorter/fashions will not last long/peak of the fashion cycle will be shorter.✓
- Fashion cycles will overlap with shorter intervals.✓
- This will result in more fashion fads.✓ (Any 2) (2)
Applying, moderate (Focus, page 50; Successful, page 50)
4.4.2
A constant demand to deliver newness means that new garments must be made all the time. As a result, more new/virgin fabrics must be produced. This causes pollution,✓ may use/depletes natural resources/forests✓ and increases the use of water/depletes water resources.✓ Harmful chemicals✓ are used in the production of dyes. When consumers constantly buy new garments/clothes the old ones often land in landfill sites where those that are not biodegradable may remain for a very long time✓ and cause pollution.✓ If new garments are imported they are transported that emits carbon dioxide.✓ (Any 4) (4)
Applying, difficult (Focus, page 61-63; Successful, page 67-70)
NOTE: Deduct one mark if not written in paragraph format.
4.5 Grey blazer✓ (1)
- Will keep her warm✓
- Will match the grey pants/white shirt/other items✓
- Professional/formal/smart look/appearance✓
- Classic style, can be worn for a long time✓ (Any 2)
OR
Long grey pants✓ (1) - Plain/neutral colour, can be mixed-and-matched with other clothes✓
- Professional/formal/smart look/appearance✓
- Classic style, can be kept for a long time✓ (Any 2)
OR
White long-sleeved shirt✓ (1) - Classic style, can be kept for a long time✓
- Plain/neutral colour, can be mixed-and-matched with other clothes✓
- Professional/formal/smart look/appearance✓ (Any 2) (Any 2 x 3) (6)
Evaluating, moderate (Focus, page 57-60; Successful, page61-62, 64)
[20]
QUESTION 5: HOUSING
5.1
- Payments of the principal/capital (amount borrowed)✓
- Interest✓
- Life insurance premiums✓
- Home-owner's comprehensive insurance premiums✓
- Administration fees✓ (Any 2) (2)
Remembering, easy (Focus, page 128; Successful, page 145)
5.2
- A title deed is a document that reflects the details of the ownership✓and of the property.✓
OR - A title deed is a document that proves that you are the owner of the property✓and includes the location/size of the property✓as well as the owner's particulars. (Any 2) (2)
Remembering, easy (Focus, page 128; Successful, page 146)
5.3
- A deposit is paid for the connection of water✓and electricity✓when a consumer buys a house. (2)
Remembering, easy (Focus, page 128; Successful, page 147)
5.4
- Breakdown of costs/building/legal costs.✔
- Detailed description of the materials and finishes.✔
- Exact dimensions of the house/dimensions according to the house plan.✔
- Completion date.✔
- Date and method of payment.✔
- Guarantees provided by the builder to repair/set right any structural defects/roof leaks/incorrect building/late completion of work.✔
- A clause of cancellation/suspension of the contract if either of the parties cannot adhere to it/clause indicating that if the loan application is declined/application for government subsidy is turned down, the agreement with the contractor/builder does not come to effect/falls through.✔ (Any 4) (4)
Remembering easy (Focus, page 120; Successful, page 139)
5.5
5.5.1
- This insurance will cover any losses should the permanent fixtures/home structure✓ suffer damage as a result of a natural disaster/storm/ flood,✓ an accident,✓ a burst geyser,✓ political unrest,✓ a fire✓. (Any 2) (2)
Remembering, easy (Focus, page 127; Successful, page 145)
- This insurance will cover any losses should the permanent fixtures/home structure✓ suffer damage as a result of a natural disaster/storm/ flood,✓ an accident,✓ a burst geyser,✓ political unrest,✓ a fire✓. (Any 2) (2)
5.5.2
- Household content insurance✓
- Will cover items such as electronic equipment/furniture/ clothing/curtains.✓ (2)
Applying, moderate (Focus, page 127-128; Successful, page 145)
5.6
5.6.1
- Lindiwe will not qualify✓ for a government housing subsidy.
- Lindiwe has a well-paid corporate job and she can only qualify if she earns R3 500.00 or less per month.✓
- Lindiwe is not married/has no long term partner/is single/ has no dependants and a citizen only qualifies if she/he has dependants.✓ (3)
Understanding, easy (Focus, page 130; Successful, page 149)
5.6.2 Sectional title town house.✓ (1)
- A sectional title town house in a complex is more secure/ safer/has more security✓/as she is a single woman✓ /as she travels.✓
- She will have the benefit of enjoying the communal garden✓ and swimming pool✓ without the problem of looking after them/ the body corporate will have the responsibility of maintaining the garden and swimming pool.✓
- She travels often and will have less maintenance to do✓ as the body corporate✓ maintains the exterior of her town house.✓ (4) (Any 4)
Applying, moderate (Focus, page 122-123; Successful, page 140-141)
5.7
- Buying a property is very costly/expensive as there are transfer costs/ transfer duties/transfer fees✓ and hidden costs/bond registration fees/ deeds office fees/interim rates/ initiation fee/property valuation fees/ occupational rent/ administration fees/service connection fees.✓
- Renting is cheaper in the short term/initially cheaper✓ and this enables a tenant to save✓ money for a deposit. The larger your deposit, the easier it will be to meet the financial responsibilities of owning property.✓
- A tenant pays a fixed amount over a specific period✓ and is not affected by increases in the interest rate.✓
- A tenant does not pay municipal rates/property tax./Owners pay municipal rates/property tax.✓
- A tenant does not pay for the maintenance of the property./Owners pay for maintenance.✓
- A tenant does not pay bond insurance/home owner's insurance./Owners pay bond insurance/home owner's insurance.✓
- It is easy to move after giving due notice.✓ It is thus easier to rent if you are not going to stay for long in a city/town/ know that you are going to move soon.✓ (4 x 2) (8)
Applying, moderate (Focus, page 118 and 127-128; Successful, page 137 and 146-147)
5.8
5.8.1 Functionality:
- The appliance is small and will easily fit into a small space.✓
- The appliance is not heavy and can easily be moved when the student moves.✓
- The appliance is multi-functional as the student can cook, bake and grill.✓ (Any 2)
5.8.2 Consumption of human energy:
- Solid plates are easy to clean,✓so this saves human energy.✓
- The appliance has easy-to-use control buttons.✓ (Any 2)
5.8.3 Consumption of non-human energy:
- Solid plates take a while to heat up,✓ this wastes electricity.✓
- Solid plates stay warm for several minutes after they have been turned off,✓ so food can be kept warm after cooking.✓
- There are two plate sizes, so energy can be saved if a small saucepan is used.✓
- The temperature controls are efficient as they provide more regulated heat.✓
- The oven is energy efficient as less electricity is needed✓ to heat a small oven. (Any 5)
5.8.4 Conclusion:
- The appliance will fulfil the cooking needs for a student who mostly cooks for him-/herself.✓
- This cooking appliance is suitable for a student who is moving into a small flat.✓ (Any 1) (10)
Evaluating, moderate (Focus, page 139-140; Successful, page 159-160)
NOTE: The conclusion can be at the beginning or at the end of the answer.
[40]
QUESTION 6: ENTREPRENEURSHIP
6.1
- Name of product✓
- Trade name/Trade mark✓
- Name and address of manufacturer✓
- Price/price code/bar code✓
- Product content✓
- Size/M/L/XL, etc.✓
- Care instructions✓ (Any 4) (4)
Remembering, easy (Focus, page 29; Successful, page 29)
6.2
- Creating awareness about the product or service.✓
- To attract the attention of customers./Generate customer's interest.✓
- Persuading customers to buy the product./Create the desire to possess the article/product./To convince consumers to buy the product.✓
- Expanding the market to new customers.✓
- To provide information about the product.✓ (Any 3) (3)
Remembering, easy (Focus, page 30; Successful, page 30)
NOTE: Only mark the first three answers.
6.3
Using goods and services to improve quality of life✓ and meet the needs of consumers,✓reducing the use of natural resources, toxic materials and chemicals/reducing waste✓ and pollution✓to protect the natural environment. ✓ (Any 3) (3)
Remembering, easy (Focus, page26; Successful, page 26)
6.4 Demand-based pricing strategy:
- The entrepreneur begins by establishing the price that the target market is prepared to pay for the product.✓
- The entrepreneur then works backwards and makes sure that the costs are kept as low as possible so that a profit can still be made.✓
OR
Premium pricing strategy:
- The entrepreneur prices his or her products above the average market price.✓
- The higher price will indicate to customers that the product is of a high quality/unique.✓ (2)
Remembering, easy (Premium pricing strategy: Focus, page 32; Demand-based pricing strategy: Successful, page 31)
6.5
6.5.1 Infra-structure:
- Kitchen (from her mother)✓
- Electricity✓
- Water✓
Appliances: - Equipment (from her mother) ✓ (3)
- Money for the sugar thermometer✓
Stock: - Materials/wood for the shelves that had to be built✓
- Money for the raw materials/ingredients✓ (Any 3)
Remembering, easy (Focus, page 11; Successful, page 18)
6.5.2
- The area must be well lit so that the stock can be organized and managed efficiently.✓
- Stock should be stored and arranged so that goods that are used frequently can be obtained quickly.✓
- Arrange stock according to best before date/expiry date/follow the first-in-first out principle.✓
- Check that the room has no mildew or damp/the storage area must be cool and dry.✓
- The shelves must be kept clean and free of dust.✓
- Treat the storage area for pests.✓ (Any 3) (3)
Understanding, easy (Focus, page 22-23; Successful, page 25)
6.5.3
- Must suit the meringues/suitable shape that will protect the shape of the meringue.✓
- Must be strong to protect the meringues.✓
- Suitable size for the meringues.✓
- Must keep the meringues clean/fresh/safe for the intended shelf-life.✓
- Must be airtight/ must protect the meringues from dust/ moisture/drying out/contamination.✓
- Strong enough for transportation.✓
- Easy to handle, open and close.✓ (Any 3) (3)
Understanding, easy (Focus, page 22; Successful, page 29)
6.5.4
- Human skills:
- Anati had the skills to make fudge and meringues as she learned that at school.✓ She attended a course at a cooking school✓ to help her to perfect the toffee and nougat recipes. (2)
- Consumer appeal:
- Her products appealed to the students/ the students liked her products.✓ It is easy for the students to buy the sweets directly from her.✓ They asked for a wider variety✓, such as nougat and fudge.✓ (Any 2) (2)
Understanding, moderate (Focus, page 10 – 14; Successful, page 16 - 20)
- Her products appealed to the students/ the students liked her products.✓ It is easy for the students to buy the sweets directly from her.✓ They asked for a wider variety✓, such as nougat and fudge.✓ (Any 2) (2)
6.5.5 Option 1:
Cost of one packet = R18,00 ÷ 100
= R0,18✓
R31,00 + R4,00 = R35,00 ÷ 36
= R0,97 per block✓
Cost per packet = R0,97 x 2 + R0,18
= R2,12✓
R2,12 x 120%✓ = R2,54✓
R2,12 + R2,54 = R4,66✓
Selling price of one packet = R5,00✓
Option 2:
Cost of one packet = R18,00 ÷ 100
= R0,18✓
R31,00 ÷ 36 = R0,86 per block
R4,00 ÷ 36 = R0,11 per block
R0,86 + R0,11 = R0,97 per block✓
Cost per packet = R0,97 x 2 + R0,18
= R2,12✓
R2,12 x 120%✓ = R2,54✓
R2,12 + R2,54 = R4,66✓
Selling price of one packet = R 5,00✓
Option 3:
Cost of one packet = R18,00 ÷ 100
= R0,18✓
R31,00 + R4,00 = R35,00 ÷ 18
= R1,94 per packet✓
Cost per packet = R0,18 + R1,94
= R2,12✓
R2,12 x 120%✓ = R2,54✓
R2,12 + R2,54 = R4,66✓
Selling price of one packet = R 5,00✓ (7)
NOTE: The rand (R) value must be indicated. Penalise (-1) only once.
Applying, moderate (Focus, page 37-38; Successful, page 38-39)
6.5.6
- In December, January, April and July, students are on holiday,✓ therefore she has a lower income during these months. During these months her production costs increase because she produces products during the holidays.✓
- In February, March, May, August, September and October, students are on campus and she is selling her products,✓ therefore she has a higher income during these months. During these months her production costs decrease as she produces fewer products while she is studying.✓ (4)
Analysing, moderate (Focus, page 39; Successful, page 41)
6.5.7
- She must save some of her profit✓ during the months that she earns well/February, March, May, August, September and October, for the ingredients she needs to buy during her production months.✓
- During the holiday months/December, January, April and July she can sell her products on the nearby flea market✓ to increase her income.
- Anati can make special holiday packaging to sell in the community/on the flea market during December/festive holiday.✓
- She can continue selling her products on campus during the holidays if there are sports training/workshops/ conferences.✓
- She can ask for orders for birthdays or special occasions.✓ (Any 4) (4)
Creating, moderate (Focus, page 35; Successful, page 34)
[40]
GRAND TOTAL: 200
CONSUMER STUDIES GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
CONSUMER STUDIES
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
INSTRUCTIONS AND INFORMATION
- This question paper consists of SIX questions.
QUESTION
CONTENT
MARKS
TIME (minutes)
1
Short Questions (All topics)
40
20
2
The Consumer
20
20
3
Food and Nutrition
40
40
4
Clothing
20
20
5
Housing
40
40
6
Entrepreneurship
40
40
TOTAL:
200
180
ALL the questions are COMPULSORY and must be answered in the ANSWER BOOK.
Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use a calculator.
- Write in black or blue ink only.
- Pay attention to spelling and sentence construction.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: SHORT QUESTIONS
1.1 Various options are provided as possible answers to the following questions. Write down the question number (1.1.1–1.1.20), choose the answer and make a cross (X) over the letter (A–D) of your choice in the ANSWER BOOK.
EXAMPLE: 1.1.21 ![]()
1.1.1 A disadvantage of organic farming:
- Crops cannot be grown in winter.
- Less land is required for growing.
- Weeds are difficult to control.
- Yields of crops are higher. (1)
1.1.2 One is advised to eat more fatty ... to limit the risk of coronary heart disease.
- beef
- chicken
- mutton
- fish (1)
1.1.3 This drink may be taken with a meal to prevent osteoporosis:
- Black tea
- Energy drink
- Flavoured milk
- Grape juice (1)
1.1.4 To manage anaemia, this drink should be AVOIDED when eating a meal:
- Coffee
- Milk shake
- Orange juice
- Sparkling water (1)
1.1.5 Which nutrition-related condition is depicted in the diagram below?
- Dairy intolerance
- Hyperglycaemia
- Hypertension
- Gluten allergy (1)
1.1.6 Many people wore Springbok jerseys or T-shirts during the 2015 Rugby World Cup. This shows the influence of … factors on fashion.
- economic
- political
- social
- technological (1)
1.1.7 Eco-fashion implies that …
- chemical dyes were used to colour fabrics for garments.
- inorganically grown cotton is environmentally friendly.
- only synthetic fibres are used to manufacture garments.
- the manufacturing process does not harm the environment. (1)
1.1.8 A lease is a contract between a …
- tenant and a property owner.
- builder and a land owner.
- property owner and the municipality.
- bank and a property buyer. (1)
1.1.9 The monthly fee that a homeowner must pay:
- Interim rates
- Property rates
- Registration fee
- Transfer fee (1)
1.1.10 The body corporate in a sectional title complex …
- has the final say about who occupies the units.
- may consist of some people who do not own the units.
- is not involved in the day-to-day running of the complex.
- must consist of at least two lawyers. (1)
1.1.11 The payment method that gives a consumer the best chance of getting a discount when he/she buys household appliances:
- Cash
- Credit account
- Credit card
- Layby (1)
1.1.12 A washing machine with an A rating is desirable because it …
- is a water-saving appliance.
- is an electricity-saving appliance.
- saves human energy.
- shows good universal design. (1)
1.1.13 A factor that is a requirement for high-quality products:
- Interesting selling place
- Creative advertising
- Meticulous control of finances
- Careful storing of products (1)
1.1.14 Negative effect of brand piracy:
- Creates competition in the market
- The image of brand holders is improved
- Registered trademarks increase their profits
- Registered trademarked goods do not enter the market (1)
1.1.15 A cash flow projection …
- shows the movement of money in a future period.
- identifies the sales targets for the next few weeks.
- is a detailed description of a marketing plan.
- is a list of all the expenses incurred. (1)
1.1.16 Which entrepreneur made a bad choice with regard to the availability of raw materials?
- Bonita buys all her raw materials in a nearby town.
- Lindiwe's raw materials are delivered monthly from the city.
- Sihle's raw materials are produced locally.
- Pete imports high-quality raw materials from Somalia. (1)
1.1.17 The factor that clearly influences the efficient production of the products of an entrepreneur who moves to larger premises to be more organised:
- Consumer appeal
- Hygiene of workers
- Tidy workspace
- Efficient use of time (1)
1.1.18 … is the consequence of an increase in the cost of electricity.
- A decrease in the consumer price index
- An increase in the inflation rate
- An increase in income tax
- A rise in interest rates (1)
Read the information below and answer QUESTIONS 1.1.19 and 1.1.20.
JOHANNESBURG – The Monetary Policy Committee has hiked interest rates by 25 basis points. [Source: eNCA, 20 August 2015] |
1.1.19 The definition for interest rate:
- A form of tax paid by banks for lending money to consumers when they do not pay money back on time.
- It is the inflation caused by borrowing money from investors who put their money in the banks.
- The amount of money that financial institutions or credit providers charge for the use of money.
- The licence to use someone else's deposited money and return it to the bank with profit. (1)
1.1.20 The meaning of 'the market has factored in the 25-basis-point hike':
- Businesses have not increased the prices of goods and services for the consumer.
- The business sector has increased prices for goods and services.
- The consumer price index has been calculated by the Reserve Bank to become 6,25%.
- The Reserve Bank has raised the inflation rate in South Africa to 6,25 basis points. (1)
1.2 Indicate the type of food additive that is used in each of the descriptions below. Write down only the word/term next to the question number (1.2.1–1.2.3) in the ANSWER BOOK.
1.2.1 Additives added to margarine to mix oil and water permanently (1)
1.2.2 Additives used in frozen yoghurt to prevent large crystals (1)
1.2.3 Additives added to freshly milled flour to change the yellowish tint (1)
1.3 Identify FOUR characteristics of universal design in dishwashers. Write only the letters (A–H) next to the question number (1.3) in the ANSWER BOOK.
- Low water consumption
- Easy to repair
- Have a low carbon footprint
- Flexible and adaptable racks
- Energy-saving switch
- Different wash programmes
- Not noisy when operated
- Auto open when programme is complete (4)
1.4 Choose the description from COLUMN B that matches the term in COLUMN A. Write only the letter (A–G) next to the question number (1.4.1–1.4.4) in the ANSWER BOOK, for example 1.4.5 H.
COLUMN A | COLUMN B |
1.4.1 Capital |
|
(4 x 1) (4)
1.5 Choose the description from COLUMN B that matches the term in COLUMN A. Write only the letter (A–F) next to the question number (1.5.1–1.5.4) in the ANSWER BOOK, for example 1.5.5 G.
COLUMN A | COLUMN B |
1.5.1 Illegal stokvel |
|
(4 x 1) (4)
1.6 Select FIVE CORRECT statements regarding the photograph below. Write only the letters (A–J) next to the question number (1.6) in the ANSWER BOOK.
The woman is wearing a sleeveless shift dress with three different colours. The dress is dark blue from the shoulders to the middle of the thigh with a 5 cm white strip below the dark blue and a 20 cm blue-green strip which ends just above the knee. The man is wearing blue jeans with a white and blue check shirt and a light blue blazer. [Source: www.truworths.co.za] |
- The blazer is a classic fashion item.
- The blazer is a good example of retrospective fashion.
- The colour of the blazer creates the illusion that the man's figure is more slender.
- The colour of the dress creates the illusion that the woman's figure is slender.
- The dress is a fashion fad.
- The dress draws attention to the woman's legs.
- The dress is suitable for a professional job.
- The dress shows harmony of colour.
- The man's whole outfit is suitable for a professional job.
- The man's jeans are suitable for formal occasions. (5)
[40]
QUESTION 2: THE CONSUMER
2.1 Read the information below and answer the questions that follow.
TAX REMINDER If you are a non-provisional taxpayer, you must file your tax return (or ITR12) on eFiling (using the eFiling platform or electronically with the assistance of an official at a SARS branch) by Friday 27 November 2015. Provisional taxpayers have until Friday 29 January 2016 to submit their tax returns. [Source: Weekend Argus, 31 October 2015] |
2.1.1 State to whom tax returns must be submitted. (1)
2.1.2 Give another term for non-provisional tax. (1)
2.1.3 Copy the table below into the ANSWER BOOK and compare non-provisional tax and provisional tax.
NON-PROVISIONAL TAX | PROVISIONAL TAX | |
Regularity/Type of income earned | (1) | (1) |
How often is the tax paid? | (1) | (1) |
(4)
2.2 Explain the term exemption clause. (2)
2.3 Read the information below and answer the questions that follow.
The government provides free electricity of 50 kWh per household, for basic needs. |
2.3.1 State TWO basic uses that this electricity is sufficient for. (2)
2.3.2 Explain how households could save on electricity, with specific reference to geysers. (2)
2.4 Read the extract below and answer the question that follows.
GASPING AT THE TILL AS GROCERY BILL BALLOONS South African consumers are constantly facing increasing food prices. The reasons are:
[Adapted from Sunday Times, 11 May 2014] |
Explain how the factors above contribute to consumers digging deeper into their pockets. (4)
2.5 Study the e-mail below that a consumer received and answer the question that follows.
Elite Loans is currently offering loans at a 4,00% interest rate in the End-of Year Special Loan Offer. To be a part of this limited offer, you are required to forward the following details via e-mail to This email address is being protected from spambots. You need JavaScript enabled to view it.: your ID number, full names, occupation, monthly income, type of loan, telephone number and e-mail address. |
Analyse the e-mail and explain, with good reasons, how a consumer should respond to this opportunity. (4)
[20]
QUESTION 3: FOOD AND NUTRITION
3.1 Give THREE reasons why antioxidants are used as food additives. (3)
3.2 Give TWO guidelines to reduce the risk of dysentery being transmitted through water. (2)
3.3 Discuss TWO reasons for food irradiation of fruit and vegetables. (2 x 2) (4)
3.4 Answer the following questions about diabetes.
3.4.1 Give a brief description of the condition diabetes. (3)
3.4.2 Explain what the consumer can do to prevent type 2 diabetes. (5)
3.5 Discuss how a high intake of fruit and vegetables will contribute to the management of anaemia. (2)
3.6 Read the scenario below and answer the questions that follow.
Saul is a 36-year-old bachelor who very seldomly cooks and regularly eats a lot of junk food. He always sprinkles extra salt on his food. |
3.6.1 Give a brief description of the cause of hypertension. (2)
3.6.2 Explain how Saul could reduce the amount of salt in his diet to prevent hypertension. (5)
3.7 Copy the table about the management of obesity below into the ANSWER BOOK and complete it.
CRITERIA | GUIDELINE TO PREVENT OBESITY | HEALTHIER ALTERNATIVE |
Cooking methods used | (1) | (1) |
Carbohydrate intake | (1) | (1) |
(4)
3.8 A business runs a food and beverage canteen for employees. A popular light snack is sandwiches with a choice of fillings.
From the list below select a suitable combination for an employee suffering from coronary heart disease and motivate your choice.
ONE TYPE OF BREAD | ONE SPREAD | ONE PROTEIN FILLING | TWO ACCOMPANIMENTS |
|
|
|
|
(5 x 2) (10)
[40]
QUESTION 4: CLOTHING
4.1 List the qualifying criteria for manufacturers to place the fairtrade logo below on their clothes.

4.2 Name TWO technological factors that influence fashion change. (2)
4.3 Write a paragraph to explain how a young adult's choice of clothing contributes to first impressions when he/she goes for a job interview. (3)
4.4 Read the statement below and answer the questions that follow.
Consumers always look for new fashion trends. |
4.4.1 Explain the effect that the constant consumer demand for new fashion trends will have on fashion cycles. (2)
4.4.2 Write a paragraph to explain the negative impact that the constant consumer demand for new fashion trends may have on the natural environment. (4)
4.5 Suraya is short and stout. She has to select TWO items in the list below to wear to a business presentation. Give TWO reasons for EACH choice.
|
(2 x 3) (6)
[20]
QUESTION 5: HOUSING
5.1 Name TWO costs that are included in monthly bond repayments. (2)
5.2 Define the term title deed. (2)
5.3 Municipalities require new homeowners to pay service-connection fees. Explain what these fees are used for. (2)
5.4 State the information that should be in a contract signed by the builder and the property owner. (4)
5.5 Answer the following questions about homeowner's insurance.
5.5.1 Explain what is covered by homeowner's insurance. (2)
5.5.2 Name and describe another type of insurance, NOT mentioned in QUESTION 5.5.1, that a homeowner should take out. (2)
5.6 Study the scenario below and answer the questions that follow.
Lindiwe, a South African citizen, is a young, single woman who has a well-paid corporate job that often requires her to work in other cities. She enjoys a beautiful garden and swimming, but finds it difficult to care for a garden and swimming pool as a result of her travelling. She has been sharing accommodation with a friend. She has now saved enough money for a deposit and wants to buy property. |
5.6.1 Explain whether Lindiwe would qualify for a government housing subsidy. (3)
5.6.2 Discuss which property would best meet Lindiwe's needs and circumstances. (5)
5.7 Discuss why buying is not always better financially than renting. (4 x 2) (8)
5.8 Study the information below and answer the questions that follow.
A student is renting a small flat that does not have a stove. The student sees the cooking appliance shown below in a store.
|
Evaluate the suitability of this cooking appliance for the student in terms of:
5.8.1 Functionality (2)
5.8.2 The consumption of human energy (2)
5.8.3 The consumption of non-human energy (5)
5.8.4 Conclusion (1)
[40]
QUESTION 6: ENTREPRENEURSHIP
6.1 List the information that should appear on a product label. (4)
6.2 List THREE objectives of advertisements. (3)
6.3 Explain the term sustainable production. (3)
6.4 Explain the demand-based pricing strategy OR the premium pricing strategy. (2)
6.5 Read the scenario below and answer the questions that follow.
Anati started studying at a tertiary institution after school. During the first few months on campus she noticed that the students often ate sweet treats. |
6.5.1 Identify THREE start-up needs for Anati's business in the scenario above. (3)
6.5.2 Give THREE guidelines to ensure that Anati's new storage space will be managed effectively. (3)
6.5.3 Give THREE requirements that the packaging for Anati's meringues should adhere to. (3)
6.5.4 Discuss the following factors that Anati considered in her choice of products for her small-scale production business:
- Human skills (2)
- Consumer appeal (2)
6.5.5 Anati sells two blocks of fudge per packet. Use the information below to calculate the selling price of ONE packet of fudge. Round off the selling price to the nearest rand. Show ALL calculations.
INFORMATION: Cost of ingredients to make one batch of 36 blocks of fudge: R31,00 |
(7)
6.5.6 Explain why there is a difference between Anati's income and expenditure in the months mentioned in the scenario. (4)
6.5.7 Advise Anati on how to solve her income and expenditure problem. (4)
[40]
GRAND TOTAL: 200
GRADE 12 MATHEMATICS PAPER 1 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
GRADE 12 MATHEMATICS
PAPER 1
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
MEMORANDUM
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- Consistent Accuracy applies in all aspects of the marking memorandum.
| QUESTION 1 | ||
1.1.1 | (x - 3)(x + 1) = 0 | ✔ answer (2) |
1.1.2 | √x3 = 512 | ✔x3/2
✔ squaring both sides |
1.1.3 | x(x − 4) < 0 | ✔critical values |
| 1.2.1 | x2 - 5x + 2 = 0 x = 5 ± √(-5)2 - 4(1)(2) 2(1) x = 5 ± √17 2 x = 0,44 or x = 4,56 OR x2 - 5x + 2 = 0 x2 - 5x = -2 x2 - 5x + [-5/2]2 = -2 + [-5/4]2 [x - 5/2]2 = 17/4 x = 5 + √17 or x = 5 - √17 2 2 x = 0,44 or x = 4,56 | ✔ subst correct formula
✔[x - 5/2]2 = 17/4 |
| 1.2.2 | f(x) = x2 - 5x + 2 x2 - 5x + 2 = c x2 - 5x + 2 - c = 0 b2 - 4ac < 0 (-5)2 - 4(1)(2 - c) < 0 25 - 8 + 4c < 0 4c < -17 c < -17 4 | ✔ standard form |
| 1.3 | x = 2y + 2 x = 2y + 2 | ✔ substitution ✔ simplification ✔ standard form ✔ factors ✔ y = 0 or y = - 4
✔ substitution |
| 1.4 | S = 6 x2 + 2 For S to be a maximum the denominator needs to be at a minimum. Minimum of x2 + 2 is 2 Maximum of S = 6 x2 + 2 = 6 2 = 3 | ✔ Minimum of x2 + 2 is 2 |
| [22] | ||
| QUESTION 2 | ||
| 2.1 | For geometric: OR b = ±√[-¼ ][-1] | ✔ b = - 1
|
| 2.2 | -¼ ; ½ ; -1 ; ........ OR T19 = ar18 | ✔r = – 2 ✔r = – 2 |
| 2.3 | The series is: -¼; ½ ; -1 ; 2 ; -4 ; 8 ; .............. The new positive term series: ½; 2 ; 8 ; 32 ; 128 ; .................. a = ½ r = 4  OR 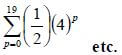 | ✔ a = ½ ✔ r = 4 ✔ 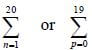 ✔ correct formula (4) |
| 2.4 | No, the series is not convergent r = 4 and for convergence –1 < r < 1 | ✔no ✔reason (2) |
| [12] | ||
| QUESTION 3 | ||
| 3.1.1 | 24 | ✔24 (1) |
| 3.1.2 |
OR Tn = T1 + (n - 1)d1 + (n - 1)(n - 2)d2 | ✔a = 3/2
✔formula |
| 3.1.3 | 3n2 - 9n + 9 = 3249 2 2 3n2 - 9n + 18 = 6498 3n2 - 9n + 6480 = 0 n2 - 3n + 2160 = 0 (n + 45)(n - 48) = 0 n ≠ −45 or n = 48 (4) | ✔ equating general term to 3249 |
| 3.2 | -1 ; 2sin3x ; 5 ; ............ 2sin3x + 1 = 5 - 2sin3x 4sin3x = 4 sin3x = 1 3x = 90º x = 30º | ✔ 2sin3x + 1 = 5 - 2sin3x ✔ sin3x = 1 ✔ 3x = 90º ✔ x = 30º (4) |
| [13] | ||
| QUESTION 4 | ||
| 4.1 | U(1 ; 0) | ✔(1; 0) (1) |
| 4.2 | x =1 | ✔x =1 |
| 4.3 | 2 + 1 = 0 x - 1 2 = -x + 1 x = -1 T(-1; 0) | ✔ y = 0 |
| 4.4 | f(x) = log5X h : x = log5 y y = 5x | ✔ change x and y |
| 4.5 | y = 0 | ✔ answer (1) |
| 4.6 | V(√2 + 1; √2 + 1) OR x = 2 + 1 OR x - 1 = 2 | ✔✔2 +1 ✔✔2 +1 (4)
✔ x = 2 + 1 ✔ subs into correct formula
✔ x = √2 + 1
|
| 4.7 | T' (3; 2) | ✔x = 3 |
| [14] | ||
| QUESTION 5 | ||
| 5.1.1 | C(0 ; –3) | ✔ C(0 ; –3) (1) |
| 5.1.2 | f(x) = x2 - 2x -3 (x - 3)(x + 1) = 0 x = -1 or x = 3 AB = 3 - (-1) AB = 4 units | ✔ factors |
| 5.1.3 | x = 2 or 2x - 2 = 0 or x = -1 + 3 2(1) 2 = 1 y = (1)2 - 2(1) - 3 = -4 D(1 ; -4) | ✔x = 1 |
| 5.1.4 | C(0 ; -3) D(1 ; -4) Average gradient = -4 + 3 or -3 + 4 1 - 0 0 - 1 = -1 | ✔ -4 + 3 or -3 + 4 1 - 0 0 - 1 ✔ -1 |
| 5.1.5 | OC = OB = 3 OR tan β = mg | ✔equal lengths |
| 5.1.6 | − 4 < k < −3 OR (–4 ; –3) | ✔–4 |
| 5.1.7 | f'(x) . f''(x) > 0 (2x - 2) . 2 > 0 2x − 2 > 0 x > 1 | ✔2x − 2 |
| 5.2 | 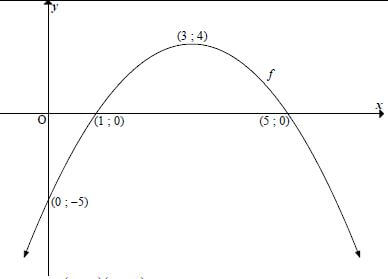 f(x) = a(x - 1)(x - 5) 4 = a(3 - 1)(3 - 5) 4 = -4a a = -1 f(x) = -x2 + 6x - 5 | TP ✔ x – intercepts |
| [22] | ||
| QUESTION 6 | ||
| 6.1.1 | A = 150 000(1 - 0,2)2 = R96 000 | ✔ n = 2 |
| 6.1.2 | 150 000(1 - 0,2)n = 49152 OR 150 000(1 - 0,2)n = 49152 n = log 0.8 1024 | ✔150 000(1 - 0,2)n = 49152
✔150 000(1 - 0,2)n = 49152 |
| 6.1.3 | R280 000 - R49 152 = R230 848 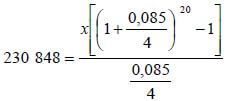 x = R9 383,26 | ✔ R230 848 |
| 6.2 | 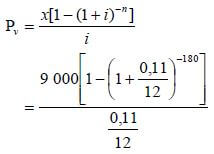 = R791 837,43 Lerato qualifies for a loan of R791 000 under the given conditions | ✔ i = 0,11
|
| [16] | ||
QUESTION 7 | ||
| 7.1 | f(x + h) = (x + h)2 - 5 = (x2 + 2xh + h2) - 5 = x2 + 2xh + h2 - 5 f(x + h) - f(x) = x2 + 2xh + h2 - 5 - (x2 - 5) = 2xh + h2 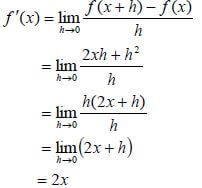 OR 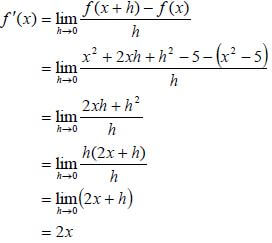 |
✔simplifying
✔formula |
| 7.2 | g(x) = 5x2 - 2x x3 = 5x2 - 2x-2 g'(x) = 10x + 4x-3 =10x + 4 x3 | ✔ 5x2 - 2x-2 ✔ 10x ✔ 4x-3 or 4 (3) x3 |
| 7.3 | h(x) = ax2 , x > 0 h-1 : x = ay2 y > 0 y = √x/a h-1 (8) = √8/a h'(x) = 2ax h' (4) = 2a(4) = 8a √8/a = 8a 64a2 = 8/a a3 = 1/8 a = 1/2 | ✔ y = √x/a ✔ √8/a ✔ h' (4) = 8a ✔ √8/a = 8a ✔ a3 = 1/8 ✔ a = 1/2 (6) |
| [14] | ||
| QUESTION 8 | ||
| 8.1 | f'(x) = 0 6x2 - 10x + 4 = 0 3x2 - 5x + 2 = 0 (3x - 2) (x - 1) = 0 x = 2/3 or x = 1 y = 2[2/3 ]3 - 5[2/3 ]2 + 4[2/3 ] y = 2(1)3 - 5(1)2 + 4(1) y = 28/27 or y = 1 Turning points are : [ 2 ; 28 ] and [1 : 1] [ 3 27] | ✔ derivative |
| 8.2 | 2x3 - 5x2 + 4x = 0 | ✔ x(2x2 - 5x + 4) = 0 ✔ x = 0 ✔ 5 ± √-7 (3) 4 ✔ x(2x2 - 5x + 4) = 0 ✔ x = 0 ✔ b2 - 4ac < 0 (3) |
| 8.3 | f(x) = 2x3 - 5x2 + 4x x(2x2 - 5x + 4) = 0 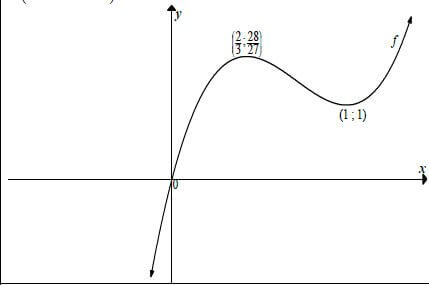 | ✔(0 ; 0) |
| 8.4 | f(x) = 2x3 - 5x2 + 4x OR x = b x > 5/6 OR Point of inflection: x = 2/3 + 1 | ✔ 12x - 10
✔ x = - (-5)
✔ x = 2/3 + 1 |
| [14] | ||
| QUESTION 9 | ||
| 9 | Length of one side of the square =x/4 Length of the rectangle 2L + x + x/4 = 6 L = 6 - 5x/4 2 = 24 - 5x 8 A = [x]2 + x[24 - 5x] [4] 4 8 = x2 + 24x - 5x2 16 32 = 24x - 3x2 32 A = 24x - 3x2 32 For minimum area dA = 0 dx dA = 24 - 6x dx 32 6x = 24 x = 4 | ✔ x/4
|
| [7] | ||
| QUESTION 10 | ||
| 10.1.1 | P(S and T) = P(S) + P(T) 1/6 = [1/4] × P(T) P(T) = 2/3 | ✔P(S and T) = P(S)×P(T) |
| 10.1.2 | P(S or T) = P(S) + P(S and T) = [1/4] + [2/3] - [1/6] =¾ | ✔ [1/4] + [2/3] - [1/6] |
| 10.2.1 | 5! | ✔ 5 |
| 10.2.2 | 55 | ✔55 or 3 125 (1) |
| 10.3 | n(E) = 5! ×2! × 2! n(S) = 7! P(E) = 5! ×2! × 2! 7! = 2 21 | ✔5! |
| [11] | ||
| QUESTION 11 | ||
| 11 |
| ✔ 0,3 |
| [5] | ||
| [150] | ||
GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
GRADE 12 MATHEMATICS
PAPER 2
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
NOTE:
- If a candidate answered a question TWICE, mark only the FIRST attempt.
- If a candidate has crossed out an attempt to answer a question and did not redo it, mark the crossed-out version.
- Consistent accuracy applies in ALL aspects of the marking memorandum. Stop marking at the second calculation error.
- Assuming answers/values in order to solve a problem is NOT acceptable.
MEMORANDUM
QUESTION 1
Ogive 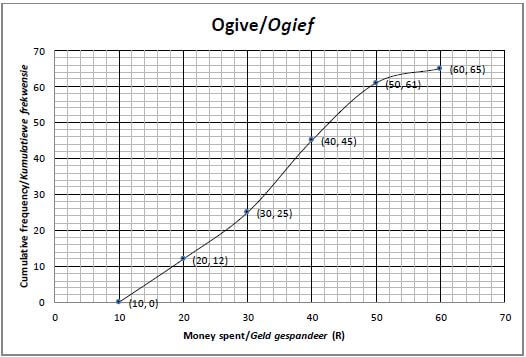
An incomplete frequency table is also given for the data.
| Amount of money (in R) | 10 ≤ x < 20 | 20 ≤ x < 30 | 30 ≤ x < 40 | 40 ≤ x < 50 | 50 ≤ x < 60 |
| Frequency | a | 13 | 20 | b | 4 |
1.1 | 65 learners | ✔ answer (1) |
1.2 | Modal class: 30 ≤ x < 40 | ✔ answer (1) |
1.3 | a = 12 | ✔ answer |
1.4 | No. of learners = 65 – 54 OR 65 – 55 | ✔ 54 or 55 [6] |
QUESTION 2
2.1 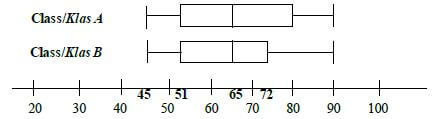
2.1.1 | IQR of Class B/IKV van Klas B = Q3 − Q1 = 72 – 51 = 21 marks/punte | ✔72 and 51 |
2.1.2 | Although the boxes contain the same number of data points, the marks for Class A are more widely spread | ✔✔ Class A is more widely spread (2) |
2.1.3 | Medians are the same | ✔✔any TWO of the 3 reasons mentioned (2) |
2.2
COUPLE | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
JUDGE 1 | 18 | 4 | 6 | 8 | 5 | 12 | 10 | 14 |
JUDGE 2 | 15 | 6 | 3 | 5 | 5 | 14 | 8 | 15 |
2.2.1 | a = –0,03 | ✔ value a |
2.2.2 | yˆ= –0,03 + 0,93(15) | ✔ substitution |
2.2.3 | Yes OR they are consistent, because r = 0,9. (r = 0,89567…) | ✔ statement [13] |
QUESTION 3 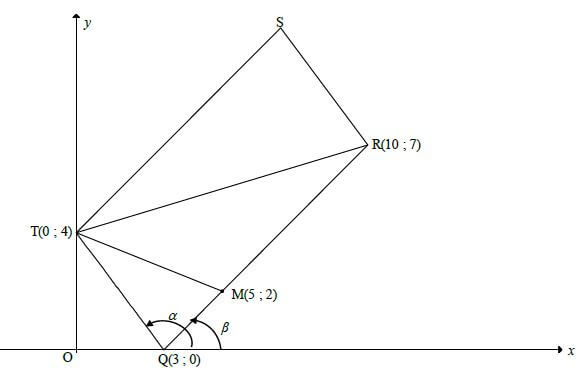
3.1 | mTQ = 4 - 0 | ✔ answer (1) |
3.2 | d = √(x2 - x1)2 + (y2 - y1)2 | ✔substitution |
3.3 | mFQ = mTQ 4k −12 = 24 | ✔ equating gradient
✔ gradient |
| 3.4 | Using transformation: | ✔✔ x–value
|
| 3.5 | TSR = TQR [opp∠ s of ΙΙ] OR TQ = SR = 5 | ✔TQR = α −β ✔ tanα = mTQ ✔ α ✔ tan β = mRQ
✔ length of TQ OR SR |
| 3.6.1 | MQ = √(5 - 3)2 + (2 - 0)2 MQ = √8 MQ = √8 RQ √98 =2/7 OR 0,29 Answer only; full marks | ✔substitution |
| 3.6.2 | area of ΔTQM = ½.QM. ⊥h [⊥h same] OR area of ΔTQM = QM OR area of ΔTQM = ½.QM. ⊥h OR area of ΔTQM = ½.QT.QM. sin(α - β) | ✔ area of ΔTQM = 2
✔ ½.QM. ⊥h [23] |
QUESTION 4 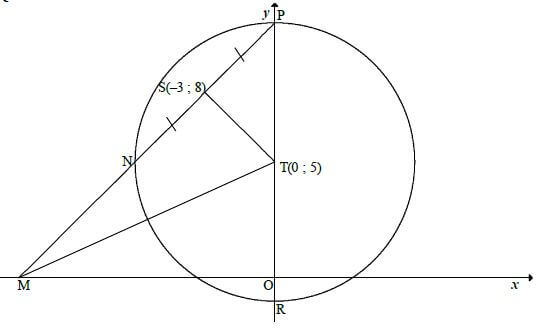
QUESTION 6
4.1 | line from centre to midpt of chord | ✔ answer (1) |
4.2 | mST = 8 - 5 | ✔ subst (–3 ; 8) and (0 ; 5) into gradient formula |
4.3 | P(0 ; 11) [y-intercept of chord NP] | ✔ coordinates of P |
4.4 | M(–11 ; 0) [x–intercept of NP] | ✔✔ coordinates of M |
| 4.5 | MT = diameter [conv ∠ in ½ circle] radius = √146 units 2 Centre of circle = midpoint MT =[ -11 ; 5] [ 2 2 ] Equation of circle through S, T and M: =[ x + -11 ]2 + [ x - 5 ]2 = 146 [ 2 ] [ 2] 4 OR =[ x + 5½ ]2 + [ x - 2½]2 = 73 2 =6,04 | ✔ radius of circle |
| [19] | ||
| QUESTION 5 | ||
| 5.1 | a = −1 | ✔ answer |
| 5.2 | f(3x)= – sin 3x | ✔360º |
| 5.3 | x ∈ [90º ; 135º) ∪ {180º} | ✔ 90º and 135º in interval form |
| [7] | ||
| QUESTION 6 | ||
| 6.1.1 | sin (360º – 36º) = – sin 36º | ✔ answer (1) |
| 6.1.2 | cos 72º = cos(2×36º) | ✔ double angle |
| 6.2 | R.T.P.: 1 - tan2θ = cos2θ OR LHS = 1 + tan2θ - tan2θ OR LHS = 1 - [sin2θ ÷ (1 + sin2θ)] | ✔writing as a single fraction
✔writing as a single fraction
✔ quotient identity |
| 6.3 | cos2½x = ¼ OR | ✔✔ cos2½x = ¼ |
| 6.4.1 | sin(A −B)= cos[90º − (A − B)] OR sin(A −B)= cos[90º − (A − B)] | ✔ co–ratio
|
| 6.4.2 | sin(x + 64º)cos(x + 379º) + sin(x + 19º)cos(x + 244º) = sin(x + 64º)cos(x + 19º) + sin(x + 19º)[-cos(x + 64º)] = sin(x + 64º)cos(x + 19º) - cos(x + 64º)sin(x + 19º) = sin[x + 64º - (x + 19º)] = sin 45º = 1 √2 | ✔cos(x + 379º) = cos(x +19º) |
| [23] | ||
QUESTION 7
7.1 | sin 27º = CD | ✔ substitution in correct trig ratio |
7.2 | cos 40º = 10 | ✔substitution in correct trig ratio |
7.3 | AC2 = CE2 + AE2 - 2CE.AE(cos AEC) | ✔ correct use of cosine rule in ΔACE
|
| [8] |
QUESTION 8 
8.1 | ˆQ = 72° [opp ∠s of cyclic quad] | ✔ S |
8.2 | R2 = P1 [∠s opp equal sides] | ✔ S/R |
8.3 | P2 = 42° | ✔ S |
8.4 | R3 = P1 + P2 OR R1 =180° −108° − 42° = 30° | ✔ R ✔ R1 = 30°
|
| [8] |
QUESTION 9 
9.1.1 | ST = SW [prop theorem ; TW || QP] | ✔ S |
9.1.2 | SV = SW | ✔ answer (1) |
9.2 | ST= SV [both equal WS /PW ] | ✔ S |
9.3 | ΔVWS ||| ΔRPS | ✔ ΔRPS (any order) (1) |
9.4 | WV = SW [ ΔVWS ||| Δ RPS] OR WV = SV [ ΔVWS ||| Δ RPS] | ✔ ratio |
| [10] |
QUESTION 10
10.1 
| 10.1 | Constr : | ✔ construction |
10.2 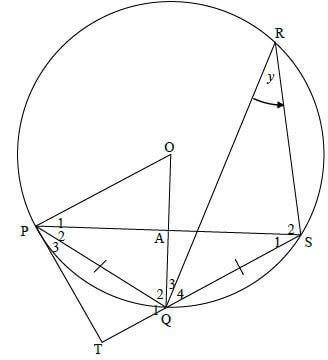
10.2.1 | ∠s in the same segment | ✔ R (1) |
10.2.2 | P2 = S1 = y [∠s opp equal sides] | ✔ S ✔ R |
10.2.3 | POQ = 2S1 = 2y | ✔ S ✔ R (2) |
10.2.4 | TPA = P2 + P3 = 2y [proved in 11.2.2] | ✔TPA = POQ |
| 10.2.5 | OPQ + OQP = 180º - 2y [sum of∠ s/e in Δ] OR OTP = 90º [radius ⊥ tangent] OR POSQ is a kite OR In ΔOAP and ΔOAS | ✔ S ✔ S ✔ R ✔✔✔ S ✔ S |
| [19] |
QUESTION 11 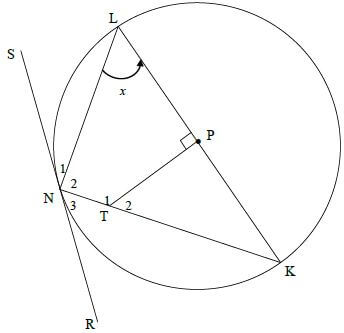
11.1 | N2 = 90° [∠ in semi-circle] OR N2 = 90° [∠ in semi-circle] | ✔ S ✔ R ✔ S ✔ R |
11.2 | T2 = PLN = x [ext ∠ of cyclic quad] OR K = 90° − x [sum of ∠s/e in ∆] OR N3 = x [tan chord theorem] | ✔ R ✔ R ✔ R |
| 11.3.1 | In ΔKTP and ΔKLN: OR In ΔKTP and ΔKLN: | ✔ S ✔ S |
| 11.3.2 | KT= KP [||| Δs] | ✔ S/R |
| [14] | ||
| TOTAL | [150] | |
GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
GRADE 12 MATHEMATICS
PAPER 2
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions in the ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs et cetera that you have used in determining your answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The amount of money, in rands, that learners spent while visiting a tuck shop at school on a specific day was recorded. The data is represented in the ogive below.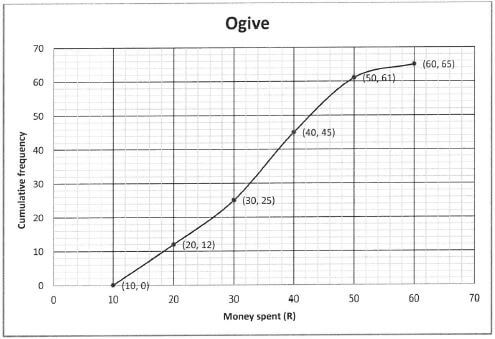
An incomplete frequency table is also given for the data.
| Amount of money (in R) | 10 ≤ x < 20 | 20 ≤ x < 30 | 30 ≤ x < 40 | 40 ≤ x < 50 | 50 ≤ x < 60 |
| Frequency | a | 13 | 20 | b | 4 |
1.1 How many learners visited the tuck shop on that day? (1)
1.2 Write down the modal class of this data. (1)
1.3 Determine the values of a and b in the frequency table. (2)
1.4 Use the ogive to estimate the number of learners who spent at least R45 on the day the data was recorded at the tuck shop. (2)
[6]
QUESTION 2
2.1 Mrs Smith has two classes, each having 30 learners. Their final marks (out of 100) for the year are represented in the box and whisker diagram below. 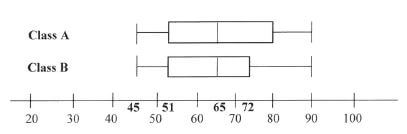
2.1.1 Determine the interquartile range of Class B. (2)
2.1.2 Explain the significance in the difference of the length of the boxes in the diagram. (2)
2.1.3 Mrs Smith studied the results and made the comment that there was no significant difference in the performance of the two classes. Give TWO reasons you think Mrs Smith will use to prove her statement. (2)
2.2 Eight couples entered a dance competition. Their performances were scored by two judges. The scores (out of 20) are given in the table below.
| COUPLE | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| JUDGE 1 | 18 | 4 | 6 | 8 | 5 | 12 | 10 | 14 |
| JUDGE 2 | 15 | 6 | 3 | 5 | 5 | 14 | 8 | 15 |
2.2.1 Determine the equation of the least squares regression line of the scores given by the two judges. (3)
2.2.2 A ninth couple entered late for the competition and received a score of 15 from JUDGE 1. Estimate the score that might have been assigned by JUDGE 2 to the nearest integral value. (2)
2.2.3 Are the judges consistent in assigning scores to the performance of the couples? Prove your answer and support it with relevant statistics. (2)
(13)
QUESTION 3
In the diagram, Q(3;0), R(10 ; 7), S and T(0; 4) are the vertices of parallelogram QRST. From T a straight line is drawn to meet QR at M(5; 2). The angles of inclination of TQ and RQ are a and β respectively. 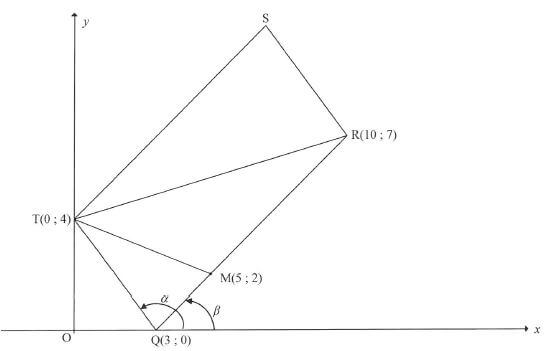
3.1 Calculate the gradient of TQ. (1)
3.2 Calculate the length of RQ. Leave your answer in surd form. (2)
3.3 F(k ; -8) is a point in the Cartesian plane such that T, Q and F are collinear. Calculate the value of k. (4)
3.4 Calculate the coordinates of S. (4)
3.5 Calculate the size of TSR. (6)
3.6 Calculate, in the simplest form, the ratio of:
3.6.1 MQ (3)
RQ
3.6.2 area of ΔTQM (3)
area of parallelogram RQTS
[23]
QUESTION 4
In the diagram, the circle, having centre T(0; 5), cuts the y-axis at P and R. The line through P and S(-3; 8) intersects the circle at N and the x-axis at M. NS = PS. MT is drawn. 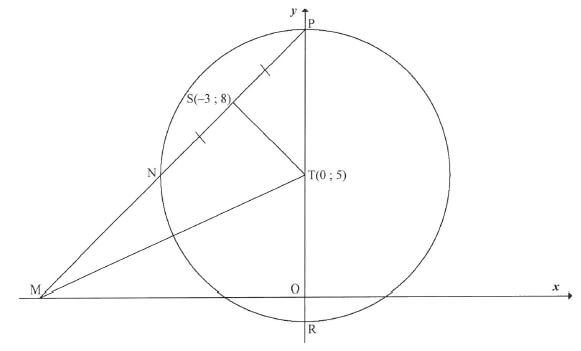
4.1 Give a reason why TS ⊥ NP. (1)
4.2 Determine the equation of the line passing through N and P in the form y = mx +c. (5)
4.3 Determine the equations of the tangents to the circle that are parallel to the x-axis. (4)
4.4 Determine the length of MT. (4)
4.5 Another circle is drawn through the points S, T and M. Determine, with reasons, the equation of this circle STM in the form (x - a)2 +(y - b)2 =r2. (5)
[19]
QUESTION 5
In the diagram, the graphs of the functions f(x)= a sin x and g(x) = tan bx are drawn on the same system of axes for the interval 0º ≤ x ≤ 225º. 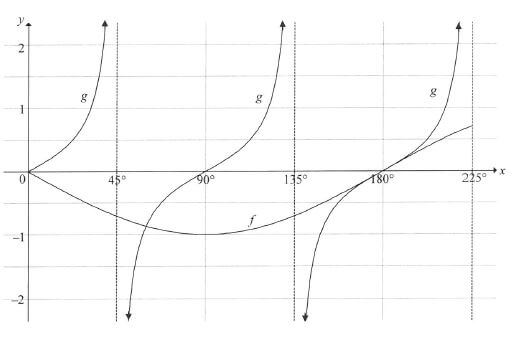
5.1 Write down the values of a and b. (2)
5.2 Write down the period of f(3x). (2)
5.3 Determine the values of x in the interval 90º ≤ x ≤ 225º for which f(x).g(x) ≤ 0. (3)
[7]
QUESTION 6
6.1 Without using a calculator, determine the following in terms of sin 36º:
6.1.1 sin 324º (1)
6.1.2 cos 72º (2)
6.2 Prove the identity: 1 - tan2θ = cos2θ (4)
1 + tan2θ
6.3 Use QUESTION 6.2 to determine the general solution of:
1 - tan2½x = 1/4
1 + tan2½x (6)
6.4 Given: cos(A - B) = cosAcosB + sinAsinB
6.4.1 Use the formula for cos(A - B) to derive a formula for sin(A - B). (4)
6.4.2 Without using a calculator, show that
sin( x + 64º) cos( x + 379º) + sin(x+19º) cos(x +244º) = 1/√2
for all values of x. (6)
[23]
QUESTION 7
In the diagram, B, E and D are points in the same horizontal plane. AB and CD are vertical poles. Steel cables AE and CE anchor the poles at E. Another steel cable connects A and C. CE = 8,6 m, BE = 10 m, AÊB = 40º, AÊC = 70º and CÊD = 27º. 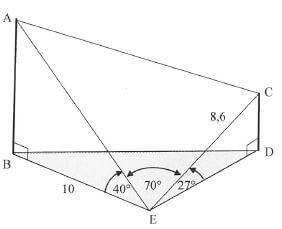
Calculate the:
7.1 Height of pole CD (2)
7.2 Length of cable AE (2)
7.3 Length of cable AC (4)
[8]
Give reasons for ALL statements and calculations in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
In the diagram, PQRS is a cyclic quadrilateral. ST is a tangent to the circle at S and chord SR is produced to V. PQ = QR, Ŝ1 = 42º and Ŝ2 = 108º. 
Determine, with reasons, the size of the following angles:
8.1 Q (2)
8.2 R2 (2)
8.3 P2 (2)
8.4 R3 (2)
[8]
QUESTION 9
In the diagram, PQRS is a quadrilateral with diagonals PR and QS drawn. W is a point on PS. WT is parallel to PQ with T on QS. WV is parallel to PR with V on RS. TV is drawn. PW: WS = 3:2. 
9.1 Write down the value of the following ratios:
9.1.1 ST (2)
TQ
9.1.2 SV (1)
VR
9.2 Prove that T1 = Q1. (4)
9.3 Complete the following statement: ΔVWS ||| Δ ... (1)
9.4 Determine WV: PR. (2)
[10]
QUESTION 10
10.1 In the diagram, O is the centre of the circle and P is a point on the circumference of the circle. Arc AB subtends AÔB at the centre of the circle and APB at the circumference of the circle. 
Use the diagram to prove the theorem that states that AÔB = 2APB. (5)
10.2 In the diagram, O is the centre of the circle and P, Q, S and R are points on the circle. PQ = QS and QŘS = y. The tangent at P meets SQ produced at T. OQ intersects PS at A. 
10.2.1 Give a reason why P2 = y (1)
10.2.2 Prove that PQ bisects TPS. (4)
10.2.3 Determine POQ in terms of y. (2)
10.2.4 Prove that PT is a tangent to the circle that passes through points P, O and A. (2)
10.2.5 Prove that OẬP = 90º. (5)
[19]
QUESTION 11
In the diagram, LK is a diameter of the circle with centre P. RNS is a tangent to the circle at N. T is a point on NK and TP ⊥ KL. PLN = x. 
11.1 Prove that TPLN is a cyclic quadrilateral. (3)
11.2 Determine, giving reasons, the size of Ñ1 in terms of x. (3)
11.3 Prove that:
11.3.1 ΔKTP ||| ΔKLN (3)
11.3.2 KT. KN = 2KT2 – 2TP2 (5)
[14]
TOTAL: 150

GRADE 12 MATHEMATICS PAPER 1 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
GRADE 12 MATHEMATICS
PAPER 1
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs et cetera that you have used in determining your answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 (x − 3)(x + 1)= 0 (2)
1.1.2 √x3 = 512 (3)
1.1.3 x (x - 4) < 0 (2)
1.2 Given: f(x)=x2 – 5x + 2
1.2.1 Solve for x if f(x) = 0 (3)
1.2.2 For which values of c will f(x) = c have no real roots? (4)
1.3 Solve for x and y:
x = 2y +2
x2 – 2xy + 3y2 = 4 (6)
1.4 Calculate the maximum value of S if S = 6 (2)
x2 + 2
[22]
QUESTION 2
Given the geometric sequence: -¼ ;b; -1; .......
2.1 Calculate the possible values of b.(3)
2.2 If b=½, calculate the 19th term (T19) of the sequence. (3)
2.3 If b=½, write the sum of the first 20 positive terms of the sequence in sigma notation. (4)
2.4 Is the geometric series formed in QUESTION 2.3 convergent? Give reasons for your answer. (2)
[12]
QUESTION 3
3.1 6; 6 ; 9 ; 15 ; ... are the first four terms of a quadratic number pattern.
3.1.1 Write down the value of the fifth term (T5) of the pattern. (1)
3.1.2 Determine a formula to represent the general term of the pattern. (4)
3.1.3 Which term of the pattern has a value of 3 249? (4)
3.2 Determine the value(s) of x in the interval xe [0°; 90°] for which the sequence -1; 2sin3x ; 5 ; ..... will be arithmetic. (4)
[13]
QUESTION 4
The sketch below shows the graphs of f(x) = log5x and g(x) = 2 + 1.
x - 1
- T and U are the x-intercepts of g and f respectively.
- The line y=x intersects the asymptotes of g at R, and the graph of g at V.

4.1 Write down the coordinates of U. (1)
4.2 Write down the equations of the asymptotes of g. (2)
4.3 Determine the coordinates of T. (2)
4.4 Write down the equation of h, the reflection of f in the line y = x, in the form y=... (2)
4.5 Write down the equation of the asymptote of h(x - 3) (1)
4.6 Calculate the coordinates of V. (4)
4.7 Determine the coordinates of T' the point which is symmetrical to T about the point R. (2)
[14]
QUESTION 5
5.1 The sketch below shows the graphs of f(x) = x2 – 2x – 3 and g(x)= x – 3.
- A and B are the x-intercepts of f.
- The graphs of f and g intersect at C and B.
D is the turning point of f.
5.1.1 Determine the coordinates of C. (1)
5.1.2 Calculate the length of AB. (4)
5.1.3 Determine the coordinates of D. (2)
5.1.4 Calculate the average gradient of f between C and D. (2)
5.1.5 Calculate the size of OČB (2)
5.1.6 Determine the values of k for which f(x) = k will have two unequal positive real roots. (3)
5.1.7 For which values of x will f'(x).F"(x) > 0 ? (3)
5.2 The graph of a parabola f has x-intercepts at x = 1 and x = 5. g(x)=4 is a tangent to f at P, the turning point of f. Sketch the graph of f, clearly showing the intercepts with the axes and the coordinates of the turning point. (5)
[22]
QUESTION 6
6.1 On the 2nd day of January 2015 a company bought a new printer for R150 000.
- The value of the printer decreases by 20% annually on the reducing-balance method.
- When the book value of the printer is R49 152, the company will replace the printer.
6.1.1 Calculate the book value of the printer on the 2nd day of January 2017 (3)
6.1.2 At the beginning of which year will the company have to replace the printer? Show ALL calculations. (4)
6.1.3 The cost of a similar printer will be R280 000 at the beginning of 2020. The company will use the R49 152 that it will receive from the sale of the old printer to cover some of the costs of replacing the printer. The company set up a sinking fund to cover the balance. The fund pays interest at 8,5% per annum, compounded quarterly. The first deposit was made on 2 April 2015 and every three months thereafter until 2 January 2020. Calculate the amount that should be deposited every three months to have enough money to replace the printer on 2 January 2020. (4)
6.2 Lerato wishes to apply for a home loan. The bank charges interest at 11% per annum, compounded monthly. She can afford a monthly instalment of R9 000 and wants to repay the loan over a period of 15 years. She will make the first monthly repayment one month after the loan is granted. Calculate, to the nearest thousand rand, the maximum amount that Lerato can borrow from the bank. (5)
[16]
QUESTION 7
7.1 Determine f'(x) from first principles if f(x) = x2 -5. (5)
7.2 Determine the derivative of: g(x) = 5x2 - 2x (3)
x3
7.3 Given: h(x) = ax2, x > 0.
Determine the value of a if it is given that h-1(8) = h' (4). (6)
[14]
QUESTION 8
Given: f(x) = 2x3 – 5x2 + 4x
8.1 Calculate the coordinates of the turning points of the graph of f. (5)
8.2 Prove that the equation 2x3 - 5x2 + 4x = 0) has only one real root. (3)
8.3 Sketch the graph of f, clearly indicating the intercepts with the axes and the turning points. (3)
8.4 For which values of x will the graph of f be concave up? (3)
[14]
QUESTION 9
A piece of wire 6 metres long is cut into two pieces. One piece, x metres long, is bent to form a square ABCD. The other piece is bent into a U-shape so that it forms a rectangle BEFC when placed next to the square, as shown in the diagram below. 
Calculate the value of x for which the sum of the areas enclosed by the wire will be a maximum [7]
QUESTION 10
10.1 The events S and T are independent.
- P(S and T)=1/6
- P(S) =¼
10.1.1 Calculate P(T). (2)
10.1.2 Hence, calculate PS or T). (2)
10.2 A FIVE-digit code is created from the digits 2; 3; 5; 7; 9.
How many different codes can be created if:
10.2.1 Repetition of digits is NOT allowed in the code (2)
10.2.2 Repetition of digits IS allowed in the code (1)
10.3 A group of 3 South Africans, 2 Australians and 2 Englishmen are staying at the same hotel while on holiday. Each person has his/her own room and the rooms are next to each other in a straight corridor.
If the rooms are allocated at random, determine the probability that the 2 Australians will have adjacent rooms and the 2 Englishmen will also have adjacent rooms. (4)
[11]
QUESTION 11
The success rate of the Fana soccer team depends on a number of factors. The fitness of the players is one of the factors that influence the outcome of a match.
- The probability that all the players are fit for the next match is 70%
- If all the players are fit to play the next match, the probability of winning the next match is 85%
- If there are players that are not fit to play the next match, the probability of winning the match is 55%
Based on fitness alone, calculate the probability that the Fana soccer team will win the next match. [5]
TOTAL: 150