Adele

Tuesday, 13 July 2021 08:38

GRADE 12 MATHEMATICAL LITERACY PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICAL LITERACY
PAPER 2
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

MEMORANDUM

MARKS: 150

Codes	Explanation
M	Method
MA	Method with Accuracy
CA	Consistent Accuracy
A	Accuracy
C	Conversion
D	Define
J	Justification/Reason/Explain
S	Simplification
RD	Reading from a table OR a graph OR a diagram OR a map OR a plan
F	Choosing the correct formula
SF	Substitution in a formula
O	Opinion
P	Penalty, e.g. for no units, incorrect rounding off, etc.
R	Rounding Off
NPR	No penalty for rounding OR omitting units
AO	Answer only

QUESTION 1 [31]

Ques.	Solution	Explanation	Level
1.1.1	Emerald – R 19 089 +✔ Onyx R 23 551 + ✔	1A Emerald 1A Onyx (2)	F L2
1.1.2	Emerald = member + adult + child = R2 477 + R1 761 + R914 ✔ = R5 152 ✔ Onyx = member + adult + child = R3 587 + R2 362 + R1 149 ✔ = R7 098 ✔ Difference = 7 098 – 5 152 ✔ = R1 946 ✔	1RT Correct values 1CA Add values 1RT Correct values 1CA Add values 1M Subtracting 1CA Difference (6)	F L2
1.1.3	Government subsidy = R5 152 – R2 530 ✔ = R2 622 Government % = 2 622 × 100 ✔ 5 152 = 50,89% = 50,9%✔	1MA Difference 1M ×100 1CA % Rounded to 1decimal place (3)	F L2
1.1.4	It is important for people to be healthy. ✔✔ OR Accept any other relevant reason.	2O Importance (2)	D L4
1.2.1	Volume = π × r² × h ✔ = 3,142 × 0,225 × 0,225 × 0,84 ✔✔ = 0,1336 m³ Volume of traditional beer = 70 × 0,1336 100 = 0,09353 m³ ✔ OR Height of container = 0,7 × 0,84 = 0,588 m ✔ Volume = π × r² × h = 3,142 × 0,225 m × 0,225 m × 0,588 m ✔✔✔ = 0,09353 m³	1M Calculating radius 1 Conversion 1SF Substitution in formula 1MA Finding 70% 1MA Finding 70% 1M Calculating radius 1A Conversion 1SF Substitution in formula (4)	M L3
1.2.2	Length of store room = 2 m = 200 cm ✔ Number of the containers along the length = 200 / 45 ✔ = 4,444… = 4 containers ✔ Width of store room = 1,5 m = 150 cm Number of the containers along the width = 150 / 45 = 3,333… = 3 containers ✔ Number of containers in total = 4 × 3 = 12 containers ✔ Statement is invalid ✔	1M Conversion 1M Dividing by 45 1CA Number of containers across the length 1CA Number of containers across the width 1CA Total number of containers 1O Invalid (6)	M L4

Ques.

Solution

Explanation

Level

1.3.1

Amount before increase = 336000/ 106,5%✔✔
= R315 492,96✔

1M Dividing
1M Using 106,5%
1CA Amount (3)

F

L2

1.3.2

Bonus = 336 000 / 12
= 28 000 ✔

Year 1 = 105,8 × 28 000 ✔
100
= R 29 624 ✔

Year 2 = 106,5 × 29 624✔
100
= R 31 549,56 ✔

1M Monthly salary
1M Using 5,8%
1CA Amount
1MA Finding 6,5%
1CA Amount (5)

F

L3

QUESTION 2 [42]

Ques.	Solution	Explanation	Level
2.1.1	10 hours = 10 × 60 = 600 minutes ✔ 1 page = 26 minutes 600 minutes = 600 / 26 ✓ = 23 pages ✔ Supposed to develop 23 papers therefore 20 papers are below norm time. ✓	1MA minutes in 10 hours 1M Dividing by 26 1CA Number of pages 1O Conclusion (4)	M L2
2.1.2	% increase = 2015 rate - 2013 rate × 100 ✔ 2013 rate = 169,30−147,36 × 100 ✔ 147,36 = 14,89 % ✔ Accept 14,9%	1M Difference 1M × 100 1CA answer % (3)	D L3
2.1.3	Amount of developing material: norm time × rate for developing × number of pages 60 = 26 × 169,30 × 161 ✓ 60 = 11 811,50 ✓ For 10 employees = 11 811,50 × 10 = 118 114,9667 ✓ Km travelled = 35×2×2×7+2×25×3×7+12×2×5×7✓ = 980 + 1 050 + 840 = 2 870 km ✓ Transport = rate for transport × number of km Amount = 2 870 × 2,82 ✓ = R8 093,40 ✓ Total amount = 118 114,9667 + 8093,40 = R 126 208,37 ✓ Balance = R130 000 - R 126 208,37 = R 3 791,63 ✓ Statement invalid; Balance less than R4 000 ✓	1SF Substituting correct values 1S Simplification 1CA For 10 people 1M Calculating distance 1CA Total distance 1M Multiplying rate per km 1CA Amount 1CA Total Amount 1CA Difference 1O Invalid (10)	M&F L4

Ques.	Solution	Explanation	Level
2.2.1	USA: 46 075,25 + 33% of amount above 189 300 ✓ = 46 075,25 + 0,33 (350 500 – 189 300) ✓ = 46 075,25 + 0,33 × 161 200 = 46 075,25 + 53 196 = 99 271,25 ✓ 12 ✓ = 8 272,60 dollars ✓	1 correct tax bracket 1 SF 1 simplification 1M dividing by 12 1CA (5)	F L3
2.2.2	Income in South Africa = $350 500 × 14,11 = R 4 945 555 ✓ Income Tax = 208 587 + 41% of amount above 701 300 ✓ = 208 587 + 0,41 × (4 945 555 - 701 300) = 208 587 + 0,41 × 4 244 255 = 208 587 + 1 740 144,55 ✓ = 1 948 731,55 – 13 257 ✓ = 1 935 474,55 / 12 = R 161 289,55 ✓ =R161 289,55/14,11 = 11430,87 dollars✓ Statement is valid ✓	1 conversion 1F Choosing correct tax bracket 1S Simplification 1M Subtract rebate 1CA Monthly Tax 1C Answer in Dollars 1O Valid (7)	L4
2.2.3	People in the higher tax brackets are feeding the government bills. ✓✓ OR It is discouraging for people occupying higher positions and earning higher salaries. ✓✓ OR People need to be treated equally✓✓ Accept any other valid reason	2R Reason (2)	D L4
2.3	Speed = distance time Time taken = 08:55 – 06:00 = 2 hours 55 minutes ✔ Less time spent in Nanaga = 2 hrs 55 min – 0 h 30 min ✔ = 2 hrs 25 minutes = 2,416666…hrs ✔ Speed = 311 2,416666✔ = 128,69 km/h✔ They travelled above the speed limit ✔	1M Travelling time 1M Difference in time 1C Conversion 1SF Substitution 1CA Speed 1O Opinion (6)	M L3
2.4	School B ✔ has performed better. The mean of School B is higher, meaning 50% of the class were able to get 56. ✔✔ Minimum mark in School B is higher. ✔✔	1M Choosing school 2 O First reason 2 O Second reason (5)	D L4

QUESTION 3 [30]

Ques.	Solution	Explanation	Level
3.1.1	✓ ✓ ✓ 58 + 279 + 45 + 455 + 232 + 303 + 280 + 49 + 498 ✓ = 2 199 km ✓	3RT (1mark for every three correct values) 1M Adding 1CA Answer (5)	M&P L2
3.1.2	N1 – South Africa ✓ N4 – South Africa ✓ A3 – Botswana ✓ A2 – Botswana✓ B6 – Namibia	4 (1 mark for route and country). If only roads mentioned max 2 If only countries mentioned max 2 (4)	M&P L2
3.1.3	OPTION 1: Accommodation = R 1 550 Breakfast = R 95 × 4 = R 380 ✓ Total amount = R 1 550 + R 380 = R 1 930 ✓ OPTION 2: Accommodation with breakfast = R 550 × 4 = R 2 200 ✓ Difference = 2 200 – 1 930 = R 270 ✓ Not true, they would save R 270 ✓	1MA Cost of breakfast 1CA Total cost 1MA Total cost 1CA Difference 1O Invalid (5)	F L4
3.1.4	Probability of getting a self-catering unit at no extra cost = 5✓ × 100 8✓ = 62,5% ✓ = 63% ✓	1A Numerator 1A Denominator 1CA % 1 R Round to nearest % (4)	P L2
3.1.5	Distance travelled = 58+98+41+41+550+105+105+738✔ = 1 736 km✓ Difference = 2199 – 1736 ✔ = 463 km✓ Statement is valid ✓	1M Adding distances 1 CA Total distance 1MA Finding the difference 1CA distance 1O Valid (5)	M&P L4
3.2.1	Percentage achievement in Mathematical Literacy is decreasing from 2013 to 2016✔✔	2 O Describing the trend (2)	D L4
3.2.2	Maths decreased from 2013 to 2015✔ Maths increased from 2015 to 2016✔	1O Description for Mathematics for 2013 to 2015 1O Description for Mathematics for 2015 to 2016 (2)	D L4
3.2.3	Mathematics = 265 810 – 263 903 = 1 907✔ Mathematical Literacy = 388 845 – 361 865 = 26 980✔ Ratio = 1 907 : 26 980✔	1A Increase in Mathematics 1A Decrease in Mathematical Literacy 1CA Ratio (3)	D L3

QUESTION 4 [47]

Ques.	Solution	Explanation	Level
4.1.1	C = 2 × π × r 157,1 = 2 × 3,142 × r ✔ 157,1 = 6,284r r = 157,1 6,284✔ = 25 cm ✔ = 0,25 m✔	1SF Substituting correct formula 1S Simplification 1CA Calculate the radius 1C Convert to metres (4)	M L3
4.1.2	D = 0,25 × 2 = 0,5 m ✔ Total height = 1 + 0,75 + 0,5 = 2,25 m ✔ Space without decoration = 4 – 2,25 = 1,75 m ✔ From top and from bottom = 1,75 2 = 0,875 m ✔	1CA finding diameter 1CA total height 1CA space without decoration 1CA (4)	M L3
4.1.3	Area for red paint = area of rectangle + area of triangle = ℓ × w + ½ b × h ✔ = 1,5 m × 1 m + ½ × 0,75 m × 0,75 m ✔ = 1,5 m + 0,28125 m = 1,78125 m² ✔ For 15 decorations = 1,78125 × 15 = 26,71875 ✔ Two coats = 26,71875 × 2 = 53,4375 m² ✔ Litres of paint needed = 53,4375 8 = 6,6796875 ✔ 5 litres = 6,6796873 5 = 1,33 = 2 (5 litres of paint) ✔ Area for white paint = πr2 + ½ b × height = 3,142 × 0,25 × 0,25 + ½ × 0,75 × 0,75 = 0,196375 + 0,28125 = 0,477625 ✔ For 15 decorations = 0,477625 × 15 = 7,164375 For 2 coats = 7,164375 × 2 = 14,32875 Litres needed = 14,32875 8 = 1,79 = 1 (5 litre) ✔ White paint = R499 ✔ Red = 505 × 2 = R 1 010 ✔ Argument not valid, cost of red paint is not twice that of white paint ✔	1M Using correct formulae 1SF Substituting 1CA Area of shaded parts 1CA area for 15 decorations 1CA for 2 coats 1MA litres of paint needed 1MA number of 5 litre tins 1CA area for white paint 1CA number 5 litre tins 1MA cost for white paint 1MA cost for red paint 1O Not valid (12)	M&F L4

Ques.	Solution	Explanation	Level
4.2.1	North East	2A Direction (2)	M&P L2
4.2.2	Mean = sum of values 21 26,762 = 22+33+34+30+25+29+23+23+22 +30+29+30+28+24+25+25+58 21✔ 26,762 × 21 = 432 + 5B ✓ 562 – 432 = 5B 130 ✔= 5B 130 = B 5 26 °C = B ✓	1SF Substitution 1M Mean value ×21 1S Simplification 1CA Value of B (4)	D L3
4.2.3	Minimum temperatures: Lower quartile (Q₁) = 8 Upper quartile (Q₃) = 11 Interquartile range = 11 – 8 = 3 ✓ Maximum temperatures: 22 22 23 23 24 25 25 25 26 26 26 26 26 28 29 29 30 30 30 33 34 ✔ Median = 26 ✔ Lower quartile = 24+25 2 = 24,5 ✓ Upper quartile = 29+30 2 = 29,5 ✓ Interquartile range = 29,5 – 24,5 = 5 ✓ Difference = 5 – 3 = 2 ✓	CA from 4.2.2 1MA Finding IQR for min. temp. 1M Ascending order 1CA Median 1MA Finding Q₁ 1MA Finding Q₃ 1CA Finding IQR 1CA Difference (7)	D L3

Ques.	Solution	Explanation	Level
4.2.4		CA from 4.2.2 and 4.2.3 5M (1 mark for every set of bars plotted correctly) 1M Correct graph (6)	D L2
4.2.5	Probability that a temperature is ≥ 28 °C = 8 ✓ 21✓ = 0,380952381 = 0,381 ✓	1A Numerator 1A Denominator 1R To 3 decimal places (3)	P L2
4.2.6	Measured distance = 6,6 cm✓ = 6,6 cm : 1 045 km✓ = 6,6 : 104 500 000✓ =1 : 15 833 333,33✓ = 1 : 16 000 000 ✓	1MA Measure on map (accept 6,4 - 6,8) 1M Ratio 1C Converting to cm 1S Simplification 1R Round to nearest million (5)	M&P L3

TOTAL: 150

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Tuesday, 13 July 2021 08:37

GRADE 12 MATHEMATICAL LITERACY PAPER 1 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICAL LITERACY
PAPER 1
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

MEMORANDUM

MARKS: 150

Symbol	Explanation
M	Method
A	Accuracy
CA	Consistent accuracy
RT/RG/RM	Reading from a table/Reading from a graph/Read from map
SF	Substitution in a formula
P	Penalty, e.g. for no units, incorrect rounding off etc.
S	Simplification
R	Rounding/Reason
NPR	No penalty for rounding

QUESTION 1 [30 MARKS]

QUES	Solution	Explanation/m	T/L
1.1.1	750 × 100% ✔ 3 200 = 23,44% ✔	1M Multiply by 100 1CA (NPR) (2)	F LI

1.1.2	Balance = 3 200 – 750 ✔ = 2 450 ✔	1M subtraction 1 CA (2)	F L1

1.1.3	Total amount paid = 750 + 5 × 300 ✔ = R2 250 ✔	1M Adding and Multiplying 1 CA (2)	F L1

1.2.1	Rate in cents = 0,8865 × 100 ✔ = 88,65 ✔	1M Multiplying 1A (2)	F L1

1.2.2	Amount charged = 50 × 88,65 ✔ = 4 432,5 cent✔ OR 50 × 0,8865✔ = R44,33 ✔	1M Multiplying 1A (NPR) (2)	F L1

1.2.3	Value Added Tax ✔✔	2 R (2)	F L1

1.3.1	Time to clock off = 7:30 + 7 hr. = 14: 30 ✔ Then 15:00 + (15 min + 45 min) = 15:30 ✔	1M adding 7hr 1A (2)	M L1

1.3.2	Income = 26 × 7 × 20 ✔ =R3 640 ✔	1M multiplication 1CA (2)	F L1

1.4.1	Distance = 1 141 km ✔✔	2RT (2)	M L1

1.4.2	East London ✔ and Polokwane ✔	2RT (2)	M L1

1.4.3	Durban ✔and Cape Town ✔	2RT (2)	M L1

1.5.1	Parents in the survey = 24 + 32 + 16 + 13 + 5 ✔ = 90 ✔	1M Adding 1A (2)	D L1

1.5.2	Less than 20% = 24 + 32 ✔ = 56 ✔	1M Adding 1A (2)	D L1

1.5.3	Modal range = 10–19 ✔✔	2RG (2)	D L1

1.5.4	Bar graph ✔✔	2RG (2)	D L1
			[30]

QUESTION 2 [42 MARKS]

QUES.	Solution	Explanation/m	T/L

2.1.1	Child support ✔✔	2RT (2)	L1

2.1.2	R1 525 + 2 x R350 ✔= R1 525 + R700 ✔ = R2 225 ✔	1MA amount 1 S 1CA amount (3)	L1

2.1.3	R1 435 x 6,27% = 89,97 ✔ R1 435 + 89,97 = R1 524,97 ✔ R1 525 ✔ OR 1435 x 1,0627 ✔= R1 524,97 ✔ = R1 525 ✔	1MA multiply by 6,27% 1CA addition 1CA Rounding 1MA multiply by 1,0627 1CA 1CA Rounding (3)	L1

2.2.1	4 x R1 155,26 ✔ = R4 621,04 ✔ OR R5 620 – (115,80 + 192,98 + 690,18) R5 620 – R998,96 ✔ = R4 621,04 ✔ OR R4 929,82 – R115,80 – R192,98 = R4 621,04	1M 1CA 1S 1CA 1M 1A (2)	L1

2.2.2	R0,00 ✔✔	2RT (2)

2.2.3	R4 621,04 x 5,6% R258,78 ✔ R4 621,04 – R258,78 R4 362,26 ✔ Price with VAT = 1,14 x 4362,26 ✔ = R4 972,98 ✔ OR 100% – 5,6% = 94,4% ✔ R4 621,04 x 94,4% R4 362,26 ✔ Price with VAT = 1,14 x 4362,26 ✔ = R4 972,98 ✔	1MA Value of 5,6% 1S Difference 1M Subtraction 1CA 1M Multiply with 1,14 Price with VAT 1M Difference in % 1 CA Value of 94,4% 1M Multiply with 1.14 1CA Price with VAT (4)	L3

2.3.1	R8,3 billion ✔✔ OR 8 300 000 000 ✔✔	2RT Penalise with 1 mark if answer is written without billion (2)	L1

2.3.2	R19,84 + R2,71 + R0,45 + R1,8 + R2,71 + R17,59 ✔ R45,1 billion ✔ OR R45 100 000 000 ✔✔	1M addition 1CA 2A Penalise with 1 mark if answer is written without billion (2)	L1

2.3.3	1 Euro = R15,3728 ? = R1,8 billion ? = 1.8 = € 0,1170899251 billion ✔ 15,3728✔ = 0,1170899251 × 1 000 000 000 = €117 089 925,1	1M division 1 CA (2)	L2

2.3.4	96,0 – 36,8 ✔✔ = 59,2 billion ✔	1M correct values 1M subtraction 1A Penalise with 1 mark if answer is written without billion (3)	L1

2.3.5	17,59 x 100% ✔ 45,1✔ = 39% ✔	1M Division 1M Multiply by 100 1CA (3)	L2

2.3.6	1,8 : 36,8 ✔✔ 1 : 20,44 ✔	1 Ratio 1 Correct values 1A (3)	L2

2.4.1	R10,00 x 25 ✔ = R250,00 ✔	1M identifying R10 1CA (2)	L1

2.4.2	260 x R1,50 ✔ = R390,00 ✔	1M 1A (2)	L1

2.4.3	R11,00 ✔✔	2RT (2)	L1

2.5.1	Inflation is the increase in prices of goods and services over time. ✔✔	2R (2)	F L1

2.5.2	Inflation rate = new prices - old prices × 100% old prices =55,95−52,95 × 100% ✔ 52,95 = 5,665 ✔ = 6% ✔	1M Substitution 1M simplification 1A Rounded in % (3)	F L2
			[42]

QUESTION 3 [23 MARKS]

QUES.	Solution	Explanation/m	T/L
3.1.1	28 + 2 × 10,6 + 41,2 + 28 ✔✔ = 118,4 g ✔	1M Addition 1M 10,6 x 2 1CA (One value missing) (3)	L2

3.1.2	Number of spoons = 2 7 , 5 ✔ 4 ,1 8 = 6,6 teaspoons ✔ = 7 teaspoons ✔	1M Division 1 CA when one of the values is incorrect 1R (3)	L1

3.1.3	50 × 500 = 25 000 250 250✔ = 100 cups ✔	1M 1A (2)	L1

3.2.1	Volume = length x width x height = 28 cm x 15 cm x 8 cm ✔ = 3 360 cm³✔	1SF 1A (2)	L2

3.2.2	Volume of chocolate =3 360 80✔ = 42 cm³✔ Volume = area of base x thickness 42 cm³ = 35 cm² x thickness ✔ Thickness of chocolate = 42 35 = 1,2 cm ✔	CA from 3.2.1 1M 1A Volume of one chocolate 1S Substitution 1A Thickness of chocolate (4)	L3

3.3.1	Diameter 130 cm + 25 cm × 2 + 1,8 cm x 2 ✔✔ = 183,6 cm ✔	1M x 2 and addition 1CA Diameter (2)	L2

3.3.2	Area = 2,3 m x 2,3 m ✔ = 5,29 m² ✔	1SF 1CA (2)	L2

3.3.3	Area = 3,142 x (0,918 m)² ✔✔ = 2,647 m² = 2,65 m²✔	1M SF 1CA radius from 3.3.1 value of diameter 1CA (3)	L2

3.3.4	Wasted material = Area of material – Area of tablecloth to cut = 5,29 m² ̶ 2,65 m²✔ = 2,64 m²✔	CA from 3.3.2 and 3.3.3 1M subtraction 1A (2)	L2
			[23]

QUESTION 4 [20 MARKS]

QUES	Solution		Explanation/m	T/L
4.1.1	Two ✔✔		2RM (2)	L1

4.1.2	Sample point E ✔✔		2 RM (2)	L1

4.1.3	Taaibuschspruit ✔ Leeuspruit ✔		1RM 1st side stream 1RM 2nd side stream (2)	L1

4.1.4	Scaled length = 3 x 100 000 25 000✔ = 25 000 ✔ = 12 cm ✔ OR 0,12 m		1M x 100 000 1M Division 25 000 1A Distance in cm (3)	L2

4.2.1	(a)	16 ✔✔	2RD (2)	L2

	(b)	Fixed side ✔ and Drop side ✔	1RD 1ste wood part 1RD 2nd wood part (2)	L2

	(c )	B ✔✔	2RD (2)	L2

4.2.2	16 ✔✔		2RM (2)	L1

4.2.3	4 ✔ 12 ✔ 1 ✔ 3		1M value of numerator 1M denominator 1M simplified answer (3)	L2
				[20]

QUESTION 5 [35 MARKS]

QUES.	Solution	Explanation/m	T/L
5.1.1	Northern Cape ✔ Western Cape ✔	2RT (2)	L1

5.1.2	A =11 705 + 5 105+4 568+10 070 + 13 022 + 5 091 + 1 963 + 3 543+3 589 ✔ = 58 656 ✔	1A adding 1CA if one value is missing (2)	L1

5.1.3	613; 1 404; 2 122; 2 149; 2 290; 2 600; 2625; 3 492; 4 765 ✔✔	2M Ascending order (2)	L1

5.1.4	2 290 ✔✔	2CA from 5.1.3 (2)	L2

5.1.5	2 625 – 1 404 ✔✔ = 1 221✔	1M correct values 1M subtraction 1CA (3)	L1

5.1.6	58 656 9 ✔ = 6 517,3 ✔ = 6 517 ✔	CA from 5.1.2 1M dividing by 9 1S 1CA (using from value from 5.1.2) (3)	L2

5.1.7	Limpopo ✔✔	2RT (2)	L1

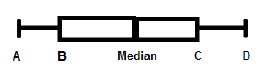
5.2.	A – Minimum value ✔ B – Lower Quartile ✔ C – Upper Quartile ✔ D – Maximum value ✔	1M Minimum 1M Lower Quartile 1M Upper Quartile 1M Maximum (4)	L2

5.3.1	Sample points 2 , 3 and 9 ✔✔	1M 1st sample point 1M 2nd and 3rd sample points (2)	L1

5.3.2	Significant risk of gastrointestinal disorders ✔✔	2RT (2)	L1

5.3.3



1 Mark per two points correctly plotted (5 x 1) 1 Mark for joining the points		(6)

5.4.1	A ---- (H;H) ✔ B----- (T) ✔ C------(T;H) ✔	3A 1 mark for each outcome	P L2

5.4.2	P(HH) =14✔✔	1M numerator 1M denominator (2)	P L2

			[35]

TOTAL:			150

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Tuesday, 13 July 2021 08:36

GRADE 12 MATHEMATICAL LITERACY PAPER 1 QUESTIONS - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICAL LITERACY
PAPER 1
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

INSTRUCTIONS AND INFORMATION

This question paper consists of FIVE questions. Answer ALL the questions.
- 2.1 Use the ANNEXURES in the ADDENDUM to answer the following questions:
  ANNEXURE A for QUESTION 1.4
  ANNEXURE B for QUESTION 4.1
  ANNEXURE C for QUESTION 4.2
  ANNEXURE D for QUESTION 5.3
- 2.2 ANSWER SHEET for QUESTION 5.3.3.
  Write your GRADE and NAMES in the spaces provided on the ANSWER SHEET. Hand in the ANSWER SHEET with your ANSWER BOOK.
Number the answers correctly according to the numbering system used in this question paper.
Start EACH question on a NEW page.
You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
Show ALL calculations clearly.
Round off ALL final answers appropriately according to the given context, unless stated otherwise.
Indicate units of measurement, where applicable.
Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise. 10. Write neatly and legibly.

QUESTIONS

QUESTION 1
1.1

Ben buys a bicycle on lay-bye for R3 200.
He pays a deposit of R750 and afterwards chose to pay R300 monthly to cover the balance.

1.1.1 Express the deposit as a percentage of the purchase price. (2)
1.1.2 Determine the balance, after the deposit has been paid. (2)
1.1.3 Determine the total amount paid after the deposit and five instalments has been paid. (2)

1.2

Karen bought 50 Kwh of electricity from her municipality in June 2017 when the tariff was 0,8865 R/Kwh (Rand per kilo-watt hour), including VAT.

1.2.1 Calculate the rate (in cents) for the tariffs charged for the 50 Kwh of electricity. (2)
1.2.2 Calculate the total amount charged for the 50 Kwh of electricity. (2)
1.2.3 Write the abbreviation VAT out in full. (2)

1.3

A care-taker at a school is paid at the rate of R26 per hour worked. He works from 7:30 am for 7 hours, excluding a 15-minute tea break and 45-minute lunch break. He does not work during weekends.

1.3.1 Determine the time when he goes off duty. (2)
1.3.2 Calculate his income if he worked for four weeks. (2)

1.4

The distances between the cities in South Africa are shown in ANNEXURE A. Use it to answer the following questions.

1.4.1 Write down the distance between Mafikeng and Port Elizabeth. (2)
1.4.2 Name TWO cities that are equal distance from Kimberley. (2)
1.4.3 Which two cities are furthest apart? (2)

1.5 A research was carried out among some parents of Zozo High School to indicate the percentage of their income they saved in June 2017. The results are shown on the graph below.

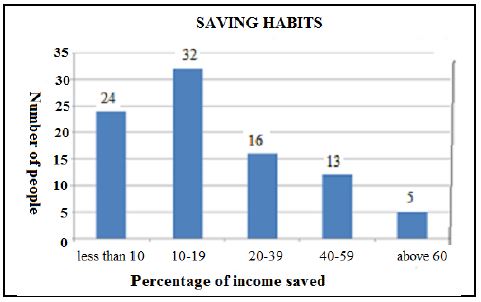1.5.1 Determine the number of people that took part in the survey. (2)
1.5.2 Calculate the number of people who saved less than 20% of their income. (2)
1.5.3 What was the modal range? (2)
1.5.4 Write down the type of graph used to display the information. (2)

[30]

QUESTION 2
2.1 In South Africa many families solely depend on social grants to sustain their livelihood. Nobuzwe, a 78-year-old grandmother lives with her four grandchildren and takes care of them. Study the information in TABLE 1 below on social grants and answer the questions that follow.

TABLE 1: MONTHLY SOCIAL GRANTS FOR FINANCIAL YEARS 2015/2016 AND 2016/2017 PER INDIVIDUAL

Types of social grants	2015/2016 (in Rand)	2016/2017 (in Rand)
State old age: (60–75 years)	1 415	1 505
State old age: (over 75 years)	1 435	1 525
War Veterans	1 435	…
Disability	1 415	1 505
Foster Care	860	890
Care Dependency	1 415	1 505
Child Support	330	350

[Adapted from People’s guide to the budget]

2.1.1 Identify the social grant that increased the least over the two financial years. (2)
2.1.2 Two of her four grandchildren received a child support grant.
Calculate the total amount of social grant Nobuzwe and the two grandchildren receive monthly for the 2016/2017 financial year. (3)
2.1.3 The War Veterans’ social grant was increased by 6,27% at the end of the 2015/2016 financial year. Calculate the monthly amount after the increase to the nearest rand. (3)

2.2 Ludwe, Nobuzwe’s son bought tyres for his expensive car from Lee Tyre and Exhaust centre in Cape Town. Study the information on the invoice below and answer the questions that follow.

Lee Tyre and Exhaust Centre: Cape Town. Tax Invoice Invoice no.: 0021548 Time printed: 11:10 Ref no.: 54383644/P Date: 02/07/2016 R – Rands VAT – Value Added Tax
Item detail	Price excluding VAT: (R)	Quantity	Net Value (R)
813750 FS TZ Firehawk tyres	1 155,26	4.000	A
BBO Wheel balance (Standard)	28,95	4.000	115,80
WWA 1 Wheel alignment	192,98	1.000	192,98

		Sub-total	4 929,82
		VAT	690,18
		Grand total	5 620,00
		Change	0,00

2.2.1 Calculate the value of A, the Net value of Firehawk tyres. (2)
2.2.2 Write down the amount Ludwe received as change. (2)
2.2.3 In August ONLY the tyres were discounted by 5,6%. Calculate how much Ludwe would have paid for the tyres, including VAT. (4)

2.3 Sasol has exploration, development, production, marketing and sales operations in 36 countries around the world. Study the revenue contributions and the total capital investments by region shown in TABLE 2 below and answer the questions that follow.

TABLE 2:

[www.sasoltechnox.co.za]

2.3.1 Write down the amount contributed to Revenue by the Rest of Africa. (2)
2.3.2 Calculate the total capital investments by Sasol in all regions. (2)
2.3.3 Convert the total capital investment in Europe into Euros. Given that 1 Euro = R15,3728 (2)
2.3.4 Calculate the difference in contribution to revenue between South Africa and Europe. (3)
2.3.5 Express the capital investment in the United States as a percentage of the total capital investments. (3)
2.3.6 Write down Europe’s capital investments, to that of Europe’s revenue contribution in the simplest ratio. Give your answer in the form: 1 : … (3)

2.4 Lerato High School had a memorial service for Anako, one of Nobuzwe grandchildren that was in Grade 10. Study the quotation from TABLE 3 below and answer the questions that follow.
TABLE 3: QUOTATION FOR PRINTING COSTS FROM THE STATIONERY SHOP PER COPY

	A3				A4
Copies	Black and White		Colour		Black and White		Colour
Quantity	S/S	D/S	S/S	D/S	S/S	D/S	S/S	D/S
1–250	R3,50	R4,00		R10,00 R12,00	R1,50	R2,00	R5,00	R6,00
251–500	R3,00	R3,50	R9,50	R11,50	R1,00	R1,50	R4,50	R5,50
501–1 000	R2,80	R3,00	R9,00	R11,00	R0,85	R1,05	R4,00	R5,00
1 000+	R2,50	R2,70	R8,50	R10,50	R0,75	R0,95	R3,00	R4,50

S/S – Single sided D/S – Double sided

2.4.1 The school will display TWENTY FOUR A3 single sided colour advertisements in the community and ONE A3 single sided colour advertisement outside the hall. Calculate the total amount the school will pay for these copies. (2)
2.4.2 The school will print 260 double sided black and white A4 programmes for the service. Calculate the total cost for the programs. (2)
2.4.3 Write down the amount charged per copy if you copy 520 A3 double sided colour copies. (2)

2.5

The prices of 1 kg of corn flakes was R52,95 in June 2016 and R55,95 in June 2017.

2.5.1 The price changes shown above are as a result of inflation. Explain the term inflation from the above context. (2)
2.5.2 Calculate the inflation rate used for the price changes on the cornflakes. Give your answer to the nearest percentage.
You may use the formula:

Inflation rate =New price – Old price x 100 (3)
Old price

[42]

QUESTION 3
3.1 Excessive sugar intake is a health hazard. Study the information about the amount of sugar in the chosen items mentioned in the TABLE 4 below and answer the questions that follow.

TABLE 4: AMOUNT OF SUGAR IN DIFFERENT CHOSEN ITEMS

Item	Amount of sugar (in grams) (g)	Capacity of an item
Sports drink	28	500 mℓ
Flavoured water	20	500 mℓ
Medium muffin	10,6	65 g
Sweetened fizzy drink	55	500 mℓ
Vitamin water	27,5	500 mℓ
Chocolate bar	41,2	80 g
1 tablespoon tomato sauce	7,4	…
Ice tea	28	330 mℓ

[Source: Discovery Vitality Kids report 2014 illustrations, Sock]
NOTE: 1 teaspoon = 4,18 g 1 cup = 250 mℓ

3.1.1 Rose drinks a can of ice tea and eats two medium muffins for breakfast, one chocolate bar at break and one sports drink after running in the afternoon. Calculate Rose’s total amount of sugar intake. (3)
3.1.2 Determine the number of teaspoons of sugar in the vitamin water drink. Give your answer to the nearest teaspoon. (3)
3.1.3 Calculate the number of cups you will get when you buy 50 bottles of sports drink for your school teams. (2)

3.2 The box shown below is used to pack 80 rectangular chocolate bars. The measurements of the box are: length = 28 cm, width =15 cm and height = 8 cm.

3.2.1 Calculate the volume of the box.
You may use the formula.
Volume = length ×width× height. (2)
3.2.2 Determine the thickness of a chocolate if the area of its base is 35 cm^2.
You may use the formula:
Volume = area of base × thickness (4)

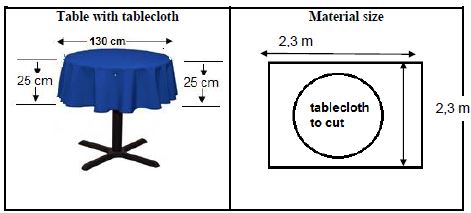
3.3 The table Lindi uses for functions in a tent has a diameter of 130 cm. The circular tablecloth used on the table overhangs 25 cm, all round. To make the tablecloth she has to add 1,8 cm right around for the hem. The tablecloth material measures 2,3 m wide and 2,3 m in length.

3.3.1 Calculate the diameter of the tablecloth to be cut from the material, including the additional centimetres for the hem. (2)
3.3.2 Calculate the area (in m2) of the tablecloth material.
You may use the formula:
Area = Length x Breadth (2)
3.3.3 Calculate the area (in m²) of a tablecloth to be cut by Lindi.
You may use the formula:
Area = π (radius)², where π = 3,142 (3)
3.3.4 Calculate the amount of material wasted when cutting the table cloth.
You may use the formula:
Wasted material = Area of a material – Area of tablecloth to be cut (2)

[23]

QUESTION 4
4.1

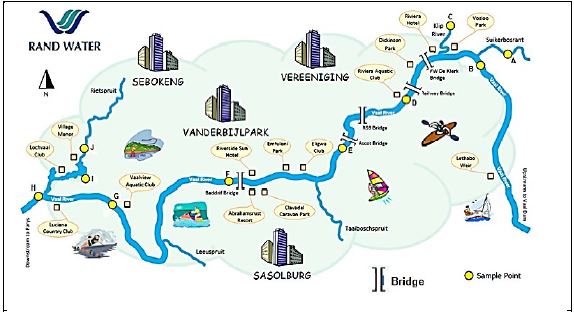
Study the map on ANNEXURE B that shows the sample points for testing Escherichia coli (E. coli) and Blue Green Algae counts per 100 mℓ.
Answer the questions that follow.

4.1.1 Write down the total number of bridges found upstream (north east) of the R59 bridge. (2)
4.1.2 Name the SIXTH sample point on the map starting from the west side. (2)
4.1.3 Lindi travelled by boat from Ascot Bridge to Vaalview Aquatic Club. Name the side streams (tributaries) to the Vaal River that she will pass. (2)
4.1.4 The distance between the R59 Bridge and Railway Bridge is 3 km. Calculate the distance on another map if the scale is 1: 25 000. (3)

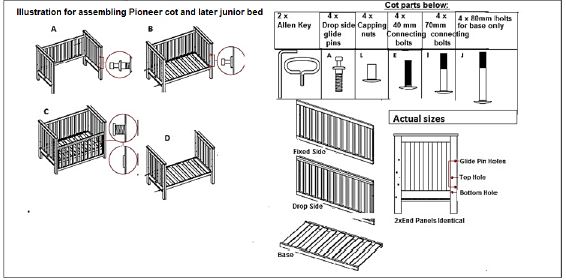
4.2 Study ANNEXURE C showing the diagrams and corresponding letters, A; B; C and D provided in order to assemble the cot and finally form a junior bed.

4.2.1

1. Write down the number of holes in the end panels. (2)
2. Name the wooden parts that must be removed, to form the junior bed. (2)
3. Which assembly illustration shows that the base is now added? (2)

4.2.2 Calculate the number of pins and bolts needed to assemble the cot. (2)
4.2.3 Determine the probability of randomly selecting an 80 mm bolt from a bag containing only the bolts. Give your answer as a simplified common fraction. (3)

[20]

QUESTION 5
5.1 TABLE 5 below shows the number of learners who were condoned to Grade 12 (made to progress to Grade 12). Study the table and answer the questions that follow.
TABLE 5: PROGRESSED LEARNERS

Province	Total number of progressed learners who
	wrote matric in 2015	passed matric in 2015	currently is in matric in 2016
Eastern Cape	11 705	2 625	18 255
Free State	5 105	2 600	7 362
Gauteng	4 568	2 149	N/A
KwaZulu-Natal	10 070	4 765	24 549
Limpopo	13 022	3 492	27 523
Mpumalanga	5 091	2 290	11 160
Northern Cape	1 963	613	2 280
North West	3 543	2 122	6 654
Western Cape	3 589	1 404	3 058
TOTAL	A	22 060	…

5.1.1 List the provinces with the number of progressed learners less than 5 000 in 2016. (2)
5.1.2 Calculate the value of A in the table. (2)
5.1.3 Arrange the number of progressed learners who passed matric in 2015 in ascending order. (2)
5.1.4 Determine the median of progressed learners who passed matric in 2015. (2)
5.1.5 Calculate the difference between the progressed learners who passed Grade 12 in 2015 from the Eastern Cape and Western Cape. (3)
5.1.6 Calculate the mean number of the progressed learners who wrote matric in 2015. Give your answer to the nearest whole number. (3)
5.1.7 Identify the province with the highest number of progressed learners in 2016. (2)

5.2 Label the box and whisker diagram by matching the terms below with the letter indicated on the diagram.

Mean; Median; Mode; Minimum; Lower Quartile; Upper Quartile; Maximum; Range

ONLY write down the letter and the correct term. (4)

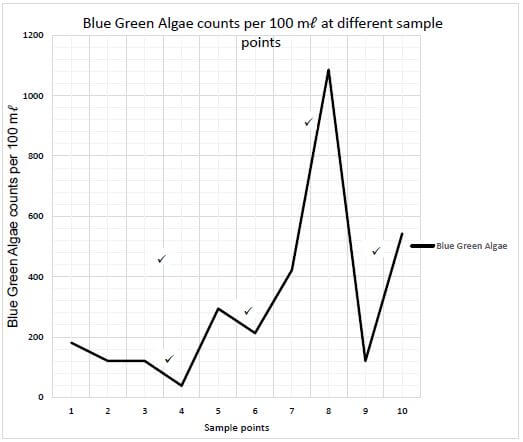
5.3 Study TABLE 6 in ANNEXURE D that shows the sample points for testing Escherichia coli (E. coli) and Blue Green Algae counts per 100 mℓ to answer the questions that follow.

5.3.1 Identify the number(s) of sample points with the same values readings for the Blue Green Algae. (2)
5.3.2 At sample point 8, the readings were 291 for E. coli counts per 100 mℓ. Write down the guideline on such readings. (2)
5.3.3 Sketch the line graph showing the readings for Blue Green Algae counts per 100 mℓ at all sample points. Use the ANSWER SHEET to draw the graph. (6)

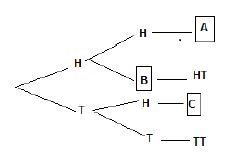
5.4 Ludwe tossed a coin twice and recorded all the possible outcomes as displayed in the tree diagram below:

5.4.1 Write down the possible outcomes represented by the letters A, B and C. (3)
5.4.2 Determine the probability of getting two heads when the coin is tossed two times. (2)

[35]
TOTAL: 150

ANSWER SHEET

GRADE 12
NAME OF LEARNER:
QUESTION 5.3.3

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Tuesday, 13 July 2021 08:35

GRADE 12 MATHEMATICAL LITERACY PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICAL LITERACY
PAPER 2
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

This question paper consists of FOUR questions. Answer ALL the questions.
Use the ADDENDUM with ANNEXURES for the following questions:
ANNEXURE A for QUESTION 1.1
ANNEXURE B for QUESTION 2.1
ANNEXURE C for QUESTION 2.2
ANNEXURE D for QUESTION 3.1
ANNEXURE E for QUESTION 3.2
ANNEXURE F for QUESTION 4.2
ANSWER SHEET 1 for QUESTION 4.2.4 which is attached to the addendum.
Write your NAME in the spaces provided on the ANSWER SHEET and hand in the ANSWER SHEET with your ANSWER BOOK.
Number the questions correctly according to the numbering system used in this question paper.
Start EACH question on a NEW page.
An approved calculator (non-programmable and non-graphical) may be used, unless stated otherwise.
Show ALL calculations clearly.
Round off ALL final answers appropriately accordingly to the given context, unless stated otherwise.
Indicate units of measurement, where applicable.
Maps and diagrams are NOT drawn to scale, unless stated otherwise. 10. Write neatly and legibly.

QUESTIONS

QUESTION 1
1.1

Mrs May is a single mother who is an educator earning R336 000 per annum. She has two children, a 19-year-old boy who is at university and a 24-year-old girl who is not studying nor working. Mrs May is a member of a medical aid scheme.
She has two options to choose from.
Study the information on ANNEXURE A to answer the questions below.

1.1.1 Identify the salary row to which Mrs May belongs for both medical aid options. (2)
1.1.2 Calculate the difference in contribution for the whole family between the two medical aid options for a month. (6)
1.1.3 If she chooses Emerald and R2 530 is deducted from her salary, calculate the percentage that the government subsidises her for medical aid. Round your answer to one decimal place.
Note: Government subsidy is the difference between medical aid amount and the amount deducted from salary. (3)
1.1.4 The medical aid scheme has a fitness exercise programme. What is the importance of such a fitness programme? (2)

1.2

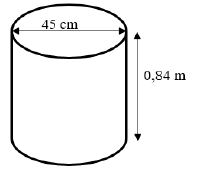
Mrs May had an initiation ceremony for her son in December 2015.
They had traditional beer brewed in big cylindrical containers with dimensions as shown below:

Containers need to be 70% full of beer to allow space for fermentation.
Note: Fermentation is a process occurring during brewing of the traditional beer which releases gas in the form of bubbles on top of the beer.

You may use the formulae:
Volume = π × radius2 × height
Area of rectangle = length × breadth
Area of circle = π × radius²
Where π = 3,142

1.2.1 Calculate the volume of the traditional beer in 1 container in cubic meters (m3). (4)
1.2.2 Mrs May has a store room which has a length of 2 m and a width of 1,5 m. She claims that she is able to pack 13 big beer containers on the floor of her store room. Verify, showing all the necessary calculations, whether her claim is valid. (6)

1.3

Mrs May is planning for her son’s graduation and decides to invest her bonus money for two years. She invests the money in an institution offering interest that is compounded annually at an interest rate of 5,8% for the first year and 6,5% for the second year.
Note: Annual bonus money is a 13th cheque which is equal to the monthly salary without deductions
Note: She only used one year’s annual bonus
Note: Her annual income is R336 000 after she received an increase of 6,5%

1.3.1 Calculate her annual income before she received the increase. (3)
1.3.2 Calculate how much money will be paid out to her after the two-year period. (5)

[31]

QUESTION 2
2.1

In 2015 people were employed to develop reading material for schools. They were paid according to the number of pages they developed. Rates and information on remuneration are given in ANNEXURE B.
They spent 7 days developing the material. They travelled daily to and from the centre where they worked. They worked 10 hours per day.

2.1.1 One of the employees developed 20 pages in 10 hours. Show, using calculations, whether the employee was within the norm time, or not. (4)
2.1.2 Calculate the percentage increase in rate of developing material from 2013 to 2015. (3)
2.1.3 The manager is convinced that the R130 000 that he has budgeted for 10 employees to each develop 161 pages in seven days will be R4 000 more than the amount needed.
Note: Two employees live a distance of 35 km from the centre; three live 25 km from the centre; and the rest live 12 km from the centre.
Verify, showing all necessary calculations, whether the manager’s statement is valid. (10)

2.2

Mr Reeva, a 58-year old USA citizen earning $350 500 taxable income per year. The USA Tax Table is shown on ANNEXURE C.

2.2.1 Calculate how much tax Mr Reeva is paying per month. (5)
2.2.2 Mr Reeva is claiming that if his earnings were taxed in South Africa, he would be paying more tax per month. Use the South African Tax Table shown in ANNEXURE C to verify whether his statement is valid.
Given that $1 = R14,11 (7)
2.2.3 From the Tax Tables, it is evident that the more you earn, the more tax you pay. Mr Reeva claims that this is unfair. Support his claim by giving ONE reason. (2)

2.3

Two friends are travelling from East London to Uitenhage which is a distance of 311 km. They leave East London at 06:00. They stop at Nanaga for 30 minutes for refreshments.

If the two friends reach Uitenhage at 08:55, show with calculations whether they did not exceed the average speed limit of 120 kilometres per hour.

You may use the formula: Speed = Distance (6)
Time
2.4

Marks are recorded and analysed after marking has been completed and marks for 2 schools are compared. In School A, the maximum mark is 87 and the minimum mark is 28 while the mean mark is 43. In School B the maximum mark is 76, the minimum mark is 53 with a mean mark of 56.

Which school has performed better? Give TWO reasons for your choice. (5)

[42]

QUESTION 3
3.1

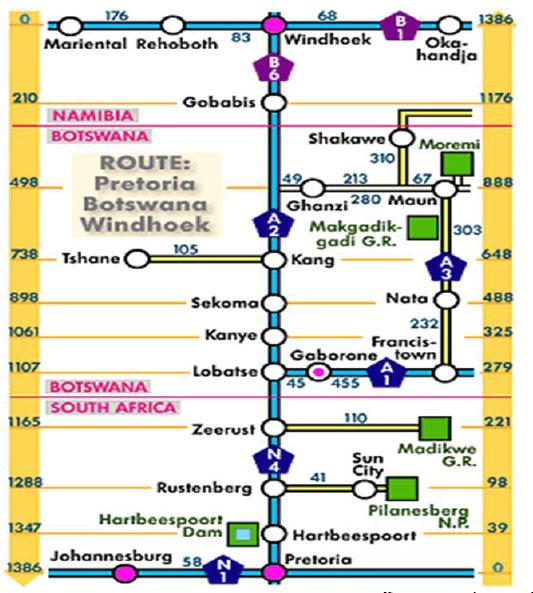
ANNEXURE D shows a strip chart from Pretoria to Windhoek.
A couple with two adult children (both females), from Johannesburg, plan a holiday and decide to go to Windhoek. On their way to Windhoek they visit the Moremi Wildlife Reserve in Maun. When travelling to Maun they turn right at Lobatse and take the A1 route and then pass through Nata. On the first day they get accommodation at Moremi Wildlife Reserve and the next day proceed to Windhoek via Ghanzi.
Use the strip chart on ANNEXURE D to answer the following questions.

3.1.1 How many kilometres do they travel to Windhoek? (5)
3.1.2 Apart from route A1, which other routes do they travel on from Johannesburg? Also, give the names of the countries where these routes are found. (4)
3.1.3

At Moremi Wildlife Reserve there are two accommodation options:
Option 1: Self-catering chalets for 4 people at R1 550 per chalet per night
Option 2: A bed and breakfast at R550 per person sharing (with breakfast)

The couple stated that if they choose Option 1 and decide to have breakfast at a restaurant at R95 per person, they will be able to save R300. Show, with the necessary calculations, whether their statement is true, or not. (5)
3.1.4

At Moremi Wildlife Reserve there are 5 self-catering units accommodating 4 people and 3 self-catering units accommodating 6 people at extra cost if there are only 4 people.

If all self-catering units are still available when they are making their booking, determine the probability of getting a self-catering unit at no extra cost. Give your answer to the nearest percentage. (4)

3.1.5

Mr and Mrs Smith, who are friends to the couple, are also on their way from Johannesburg to Windhoek. They take a different route and spend a night at Sun City. From Sun City they proceed to Tshane to visit some friends. After their visit, they travelled on the A2 route to Windhoek.

The two families are claiming that the difference between the distance travelled by the couple with the two adults and the distance travelled by Mr and Mrs Smith, is 463 km. Verify, with the necessary calculations, whether the statement is valid. (5)

3.2

The table in ANNEXURE E has information on the performance of Grade 12 learners in some of the most popular subjects from 2013 to 2016.

3.2.1 Describe the trend of the percentage achieved in Mathematical Literacy from 2013 to 2016. (2)
3.2.2 Explain how the percentage achieved for Mathematics differ from the percentage achieved for Mathematical Literacy for the period 2013 to 2016. (2)
3.2.3 In January 2017 when the Minister of Education, Angie Motshekga, announced the 2016 matric results, she mentioned that in 2016 the enrolment for Mathematics increased from 263 903 to 265 810 and that of Mathematical Literacy decreased from 388 845 to 361 865. Write the difference in the Mathematics enrolment to the difference in the Mathematical Literacy enrolment as a ratio. (3)

[30]

QUESTION 4
4.1

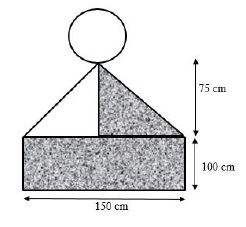
People in Mrs. Sibeko’s home village like colourful decorations.
They have decided to decorate the outside walls of their community hall as shown in the diagram below.

Notes:

Dimensions are as indicated
Circumference of the circular part is 157,1 cm
The two triangles are equal.

You may use the following formulae:

Area of rectangle = length × width
Circumference of circle = 2 × π × radius
Area of triangle = ½ × base × height
Area of circle = π × radius²; where π = 3,142

4.1.1 Calculate the diameter of the circular part of the decoration in metres. (4)
4.1.2 If the wall is 4 m high and the decorations are at equal distances from the top and the bottom, calculate the distance that the decoration is from the top and the bottom of the hall in metres. (4)
4.1.3

The decoration is painted using red paint for the shaded part and white paint for the unshaded parts. Paint is sold in 5 litre tins at R499 for the white paint and R505 for the red paint. Spreading rate for paint is 8 m²per litre. Two coats of each colour will be needed and 15 decorations will be painted.

Mr. Sibeko stated that the amount of money that they will spend for red paint will be twice the amount of money that they will spend for white paint.
Verify, with the necessary calculations, whether this statement is valid or not. (12)

4.2

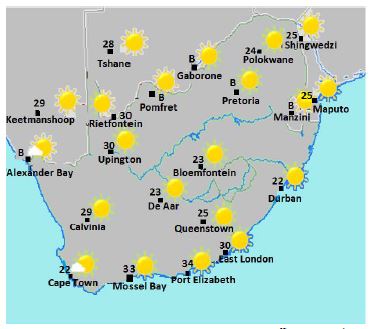
The map in ANNEXURE F is showing maximum temperatures for some towns and cities in South Africa and neighbouring countries.

4.2.1 What is the general direction of Polokwane from Calvinia? (2)
4.2.2 If the mean for the maximum temperature of all the towns and cities shown on the map is 26,762 °C, calculate the modal value B for the 5 towns and cities represented by B on the map. (4) 4.2.3

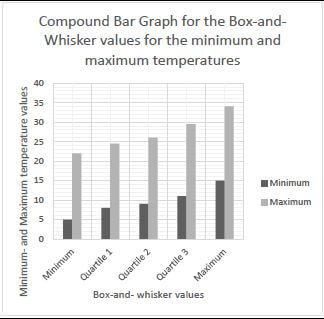
The box and whisker diagram represents the minimum temperatures: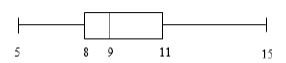

Calculate the difference between the interquartile ranges of the minimum temperatures and maximum temperatures. (7)
4.2.4 The box-and-whisker values for the minimum temperatures have already been plotted in ANSWER SHEET 1. Plot the box-and-whisker values for the maximum temperatures to complete a compound bar graph on the same ANSWER SHEET. (6)
4.2.5 Refer to the maximum temperatures as shown on the map and calculate the probability of having a temperature equal to or more than 28 °C. Give your answer as a decimal fraction to three decimal places. (3)
4.2.6 The actual distance between East London and Cape Town is 1 045 km. Calculate the scale used on the map and write it in the form 1 : ... Give your answer to the nearest million. (5)

[47]
TOTAL: 150

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Tuesday, 13 July 2021 08:34

GRADE 12 MATHEMATICAL LITERACY PAPER 2 ADDENDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICAL LITERACY
PAPER 2
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

ADDENDUM

ANNEXURE A – QUESTION 1.1
Table showing how much to pay for two different medical aid options in 2016:
EMERALD:

Salary row	R 0 – R 11 053	R 11 053 – R 19 089	R 19 089+
Member row	R 1 996	R 2 210	R 2 477
Adult row	R 1 416	R 1 583	R 1 761
Child row	R 731	R 820	R 914

ONYX:

Salary row	R 0 – R 11 053	R 11 053 – R 23 551	R 23 551+
Member row	R 3 193	R 3 322	R 3 587
Adult row	R 2 271	R 2 351	R 2 362
Child row	R 949	R 1 030	R 1 149

[Source: www.gems.gov.za]

Notes:

Salary row reflects monthly salary before tax and other deductions.
Member row shows how much the main member (person paying for the medical aid) has to pay.
Adult row shows how much you pay for adult dependent.
Child row shows how much the main member pay for child dependents (persons under the age of 21). Persons that are mentally or physically disabled, younger than 28 and still students at a recognised educational institution.

ANNEXURE B – QUESTION 2.1
Remuneration for developing reading material:

Rates for 3 consecutive years
Year	2013	2014	2015
Norm time (in minutes)	26	26	26
Rate for developing in Rand	147,36	138,25	169,30
Rate for transport in Rand	2,45 per km	2,64 per km	2,82 per km

Notes:

Norm time = number of minutes taken to develop 1 page
Total remuneration = amount of developing material + transport
Amount for developing material =
^{norm time}/₆₀ × rate for developing × number of pages developed
Transport fee = rate for transport × number of kilometres travelled

ANNEXURE C – QUESTION 2.2
Tax Tables for Individuals:
American Tax Table 2015/2016 (1 March 2015 to 29 February 2016)

IF TAXABLE INCOME IS BETWEEN:	THE TAX DUE IS:
0 – $9 225	10% of taxable income
$9 226 – $37 450	$922,50 + 15% of the amount over $9 225
$37 451 – $90 750	$5 156,25 + 25% of the amount over $37 450
$90 751 – $189 300	$18 481,25 + 28% of the amount over $90 750
$189 301 – $411 500	$46 075,25 + 33% of the amount over $189 300
$411 501 – $413 200	$119 401,25 + 35% of the amount over $411 500
$413 201 +	$119 996,25 + 39,6% of the amount over $413 200

[Source: www.incometax/p/america]

South African Tax Table 2015/2016 Tax Year (1 March 2015 to 29 February 2016)

TAXABLE INCOME (R)	RATES OF TAX (R)
0 – 181 900	18% of each R1
181 901 – 284 100	32 742 + 26% of the amount above 181 900
284 101 – 393 200	59 314 + 31% of the amount above 284 100
393 201 – 550 100	93 135 + 36% of the amount above 393 200
550 101 – 701 300	149 619 + 39% of the amount above 550 100
701 301 and above	208 587 + 41% of the amount above 701 300

Tax Rebates in South Africa

TAX REBATE	2016	2015
Primary (younger than 65 years)	R13 257	R12 726
Secondary (65 years and older)	R7 407	R7 110
Tertiary (75 years and older)	R2 466	R2 367

[Source: www.sars.gov.za]

ANNEXURE D – QUESTION 3.1
Strip chart map showing route from Pretoria to Windhoek:

[Source: www.googlemaps.co.za]

ANNEXURE E – QUESTION 3.2
Grade 12 performance of some subjects from 2013 to 2016:

	2013			2014			2015			2016
SUBJECTS	Wrote	Achieved at 30% and above	% achieved	Wrote	Achieved at 30% and above	% achieved	Wrote	Achieved at 30% and above	% achieved	Wrote	Achieved at 30% and above	% achieved
Geography	239 657	191 834	80,0	236 051	191 966	81,3	303 985	234 209	77,0	302 600	231 588	76,5
History	109 046	94 982	87,1	115 686	99 823	86,3	154 398	129 643	84,0	157 594	132 457	84,0
Life Sciences	301 718	222 374	73,7	284 298	209 783	73,8	348 076	245 164	70,4	347 662	245 070	70,5
Mathematical Literacy	324 097	282 270	87,1	312 054	262 495	84,1	388 845	277 594	71,4	361 865	257 881	71,3
Mathematics	241 509	142 666	59,1	225 458	120 523	53,5	263 903	129 481	49,1	265 810	135 958	51,1
Physical sciences	184 383	124 206	67,4	167 997	103 348	61,5	193 189	113 121	58,6	192 618	119 427	62,0

[Source: www.eduation.gov.za]

ANNEXURE F – QUESTION 4.2
Map with the maximum temperatures on 11 August 2016:

ANSWER SHEET 1 FOR QUESTION 4.2.4 [Source: www.weathersa.co.za]

NAME:............................................................................... GRADE 12: ..........................................................

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Tuesday, 13 July 2021 08:33

GRADE 12 MATHEMATICAL LITERACY PAPER 1 ADDENDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICAL LITERACY
PAPER 1
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

ADDENDUM

ANNEXURE A: QUESTION 1.4
DISTANCES IN KM BETWEEN THE CITIES IN SOUTH AFRICA

	Bloemfontein	Cape Town	Durban	East London	Johannesburg	Kimberley	Mafikeng	Port Elizabeth	Pretoria	Umtata
Bloemfontein	–	1004		584	398	177	464	681	455	570
Cape Town	1 004	–	1 753	1 079	1 402	969	1 343	769	1 460	1 314
Durban	634	1 753	–	674	557	811	821	984	636	439
East London	584	1 079	674	–	982	780	1 048	310	1 040	235
Johannesburg	398	1 402	557	982	–	476	287	1 075	58	869
Kimberley	177	969	811	780	476	–	380	743	530	747
Mafikeng	464	1 343	821	1 048	287	380	–	1 141	294	1 034
Polokwane	706	1 710	886	1 290	297	780	569	1 383	250	1 181
Port Elizabeth	681	769	984	310	1 075	743	1 141	–	1 133	545
Pretoria	455	1 460	636	1 040	58	530	294	1 133	–	928
Umtata	570	1 314	439	235	869	747	1 034	545	928	–

QUESTION 4.1 ANNEXURE B

QUESTION 4.2: ANNEXURE C

Escherichia coli (E. coli)		E. coli counts per 100 mℓ at sample points
Possible symptoms include: Skin irritations infections gastrointestinal disorders*	Sample points	1	2		3	4		5	6		7	8	9	10
	Results	236	8		649	488		140	108		16	291	1 236	28
Guideline	Low risk of gastrointestinal disorders E. coli < 130 counts/100 mℓ	Slight risk of gastrointestinal disorders E. coli 130–200 counts/ 100 mℓ					Significant risk of gastrointestinal disorders E. coli 200–400 counts/ 100 mℓ					High risk of gastrointestinal disorders E. coli >400 counts/100 mℓ

Blue Green Algae		Blue Green Algae counts per 100 mℓ at sample points
Possible symptoms include: Skin irritations, infections and gastrointestinal disorders*	Sample points	1	2		3	4		5	6		7	8	9	10
	Results	181	121		121	39		294	213		422	1 086	121	543
Guideline	Low risk Blue Green Algae < 20,000 cells/mℓ			Moderate risk Blue Green Algae 20,000–100,000 cells/mℓ						High risk Blue Green Algae >100,000 cells/mℓ

QUESTION 5.3: ANNEXURE D
TABLE 6: RESULTS OF THE TEST FOR ESCHERICHIA AND BLUE GREEN ALGAE AT DIFFERENT SAMPLE POINTS AND A GUIDELINE TO THE RISK REGARDING READINGS

[Adapted from Barrage Weekly, 03 June, www.reservoir.co.za]

*If ingested. X sample not received / no information available. Reports generated every Friday of the year.

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Monday, 12 July 2021 07:28

GRADE 12 MATHEMATICS PAPER 1 ERRATA - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICS
PAPER 1
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

The Mathematics P1 Grade 12 September was written on Friday, 15 September 2017. We were made aware of certain amendments and omissions that were discovered during the marking process.
In order to address this and to ensure that learners are not disadvantaged, the following standardised approach to marking must be adopted across the Province. The following guidelines with regard to marking was prepared in conjunction with the examiner and moderator.

ERRATA

5.5	P (⁻³ / ₂; ⁻⁹ / ₄) (⁻³ / ₂ + 2 ; ⁻⁹ / ₄) (¹ / ₂; ⁻⁹ / ₄) or f(x - 2) = (x - 2)(x - 2 + 3 ) f(x - 2) = x² - x - 2 x = - (-1) 2(1) x = ¹ / ₂	✔✔ answer ✔f(x - 2) = x² - x - 2 ✔x = ¹ / ₂ (2)
6.2	q(x) = -2^-x	✔ answer(1)

6.4	y> 0 ; y ∈ R	(1)

6.5	See 6.1	✔✓ shape and x-intercept(2)

10.2	V = 2x × x × (81 − 2x ) 2x 3 V = 81x −⁴/₃x^a	✔✓ sub. into volume formula (2)

10.3	dV = 81 - 4x² dx 81 - 4x² = 0 x² = 81 4 x = ⁹/₂ = 4.5	✔81 - 4x² ✔x² = 81 4 ✔answer(3)

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Monday, 12 July 2021 07:25

GRADE 12 MATHEMATICS PAPER 1 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICS
PAPER 1
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

NOTE:

If a candidate answered a question TWICE, mark the FIRST attempt ONLY.
Consistent accuracy applies in ALL aspects of the memorandum.
If a candidate crossed out an attempt of a question and did not redo the question, mark the crossed-out attempt.
The mark for substitution is awarded for substitution into the correct formula.

MEMORANDUM

QUESTION 1

?

1.1	2?(? + 1) − 7(? + 1) = 0 (? + 1)(2? − 7) = 0 ? = −1 or ? = 72	? factors ? ?-value ? ?-value	(3)

1.2	?² − 5? − 1 = 0 ? = −? ± √?² − 4?? 2? ? = −(−5) ± √(−5)² − 4(1)(−1) 2(1) ? = 5,19 or ? = −0,19	? substitution into correct formula ?? x- values	(3)

1.3	4?² + 1 ≥ 5? 4?² − 5? + 1 ≥ 0 (4? − 1)(? − 1) ≥ 0 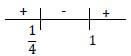x ≤ ¹/₄ or ? ≤ 1	? standard form ? factors ?? ≤ ¼ ?? ≥ 1	(4)

1.4	5^4?+3. 100^−2?+1 = 50 000 5^4?+3. (5². 2²)^−2?+1 = 50 000 5^4?+3. 5^−4?+2. 2^−4?+2 = 50 000 5⁵. 2^−4?. 2² = 50 000 2^−4? = 2²−4? = 2 ? = − ¹/₂	?5^−4?+2 ?2^−4?+2 ?−4? = 2 ? answer	(4)

1.5	? = 2? …………………..(1) ?² + 2? − ? − ?² = 36……….(2) ? = 2? sub into (2) (2?)² + 2(2?) − ? − ?² = 36 4?² + 4? − ? − ?² = 36 3?² + 3? − 36 = 0 ?² + ? − 12 = 0 (? − 3)(? + 4) = 0 ? = 3 or ? = −4 ? = 6 or ? = −8	?substitution ?standard form ? factors ? y − values ? x − values(5)	(5)

1.6	?² − ?? + ? − 1 = 0 ∆ = ?² − 4?? ∆ = (−?)² − 4(1)(? − 1) ∆ = ?² − 4? + 4 ∆ = (? − 2)² ∆ ≥ 0 roots are real and rational(perfect square)	?substitution ? simplification ? (? − 2)2 ? conclusion(4)	(4)
			[23]
QUESTION 2
2.1.1	?_? = 4? − 1 483 = 4? − 1 484 = 4? ? = 121 121 terms in series	? ?? = 4? − 1 ? equating 483 ? answer(3)	(3)

2.1.2	121 ∑ (4? − 1) ?=1	? answer	(2)

2.2.1	(? − 3) − (2? − 4) = (8 − 2?) − (? − 3) −? + 1 = −3? + 11 2? = 10 ? = 5	? setting up equation ? simplification ? answer	(3)

2.2.2	… ; … ; … 6 ; 2 ; −2 ; … ; … ; … ?₁₀ = 6 or ?? = −4? + 46 ? + 9? = 6 ?₁ = −4(1) + 46 ? + 9(−4) = 6 ?₁ = 42? = 42	? numerical values of?10; ?11; ?12 ? difference −4 ? a-value	(3)

2.3	??² + ??³ = −4 ? + ?? = −1 ??²(1 + ?) = −4 ?(1 + ?) = −1 ∴ ?² = 4 ∴ ? = ±2 ? + ?(2) = −1 ∴ ? + 2? = −1 3? = −1 ? = − ¹/₃ First three terms: − ¹/₃ ; − ²/₃ ; − ⁴/₃	? setting of equations ? common factor ? ? = 2 ? value of a ? first three terms	(6)
			[17
QUESTION 3
3.1	41 ; 43 ; 47 ; 53 ; 61 ; 71 ; 83 ; 97 ; 113 ; 131 2 4 6 8 10 12 14 16 18 2 2 2 2 2 2 2 2 2? = 2 ? + ? = 2 ? + ? + ? = 41 ? = 1 ? = −1 ? = 41 ∴ ?_? = ?² − ? + 41	? 2nd difference ? ? = 1 ? ? = −1 ? ? = 41 ? ?_? = ?² − ? + 41	(5)

3.2	?₄₁ = 41² − 41 + 41 ?₄₁ = 1681 Factors of 1681: 1 ; 41 and 1681 1681 is not a prime number	? ?₄₁ = 1681 ? factors ? conclusion	(3)

3.3	Consider the unit digits only 1 ; 3 ; 7 ; 3 ; 1 ; 1 ; 3 ; 7 ; 3 ; 1 ; groups of 5 49999998 = 9999999,6 5 0,6 × 5 = 3 ?_49999998 will end in 7	? unit digits ? groups of 5 ? conclusion	(3)
			[11]
QUESTION 4
4.1.1	? = ?(1 + ?)^? ? = 500 000 (1 + 7,2 )^12? 1200 ? = 500 000(1.006)^12?	?sub into formula ? 12?	(2)

4.1.2	? = 500 000(1.006)^12? ? = 500 000(1.006)1^2×5 ? = ? 715894.21	? ? = 60 ? answer	(2)

4.1.3	? = ?(1 + ?)^? 1000000 = 500000(1.006)^12? 12? = log 2 log 1.006 12? = 115.8707581 ? = 9,66 ????? Will exceed R1 000 000 in 10 years.	? setting up equation ? using logs ? conclusion	(3)

4.2.1	?_V = 10 000 [1 − (1 + ¹⁵/₁₂₀₀ ) ⁻³⁶] ¹⁵/₁₂₀₀ ?? = ?288 472,67 ???????/? = ?350 000 − ?288 472,67 ???????/? = ?61 527,33	? ? and ? ?sub into ?_? formula ? ?_? formuleü ?? = ?288 472,67 ? subtracting ? answer	(5)

4.2.2	350 000 = ? [1 − (1 + ^18,5/₁₂₀₀ ) ⁻⁶⁰] ^18,5/₁₂₀₀ ? = ? 8 983,17	? ? = 18,51200 ?? = −60 ? substitution ? answer	(4)
			[16]
QUESTION 5
5.1	?(−3; 0)	? answer	(1)

5.2	?(?) = ?² + 3? ? = − ? 2? ? = − 3 2 ? (− 3) = (− 3)² + 3 (− 3) 2 2 2 = − ⁹/₄ ? (− 3 ; − 9) 2 4	?? = − 32 ?substitution ?answer	(3)

5.3	?(−5) = 10 and ?(−3) = 0 ? = 10 − 0 −5 − (−3)? = −5	? calculating ?(−5) and ?(−3) ? substitution ? ?-value	(3)

5.4	? < −3 or / of ? > 0	?answer	(2)

5.5	? (− 3 ; − 9) 2 4 (− 3 − 2 ; − 9) 2 4 (− 1 ; − 9) 2 4 or ?(? − 2) = (? − 2)(? − 2 + 3) ?(? − 2) = ?² − ? − 2 ? = − (−1) 2(1) ? = − ½	? answer ? ?(? − 2) = ?² − ? − 2 ? ? = − 12	(2)

5.6	?? = − ¹/₂ ? + 2 − (?² + 3?) ?? = − ¹/₂ ? + 2 − ?² − 3? ?? = −?² − ⁷/₂ ? + 2 ?? = − (?² + ⁷/₂ ? − 2) L? = − [(? + ⁷/₄ )² − ⁸¹/₁₆ ] L? = − (? + ⁷/₄ )² + ⁸¹/₁₆ OR ?? = − ¹/₂ ? + 2 − (?² + 3?) ?? = − ¹/₂ ? + 2 − ?² − 3? ?? = −?² − ⁷/₂ ? + 2 ??? = −2? − 7 ?? 2 −2? − ⁷/₂ = 0 ? = − ⁷/₄ ? = − (− ⁷/₄ )² − ⁷/₂ (− ⁷/₄ ) + 2 ? = ⁸¹/₁₆ ∴ ?? = − (? + ⁷/₄)² + ⁸¹/₁₆ OR ? = − ? 2? ? = − [ −⁷/₂] 2(−1) ? = − ⁷/₄ ? = − (− ⁷/₄ )² − ⁷/₂ (− ⁷/₄ ) + 2 ? = ⁸¹/₁₆ ∴ ?? = − (? + ⁷/₄)² + ⁸¹/₁₆	? ?(?) − ?(?) ? standard form ? completing the square ? answer ? ?(?) − ?(?) ? standard form ? ? = − ⁷/₄ ? ? = ⁸¹/₁₆ ??(?) − ?(?) ? standard form/standaardvorm ? ? = − ⁷/₄ ? ? = ⁸¹/₁₆	(4)
			[15]
QUESTION 6
6.1		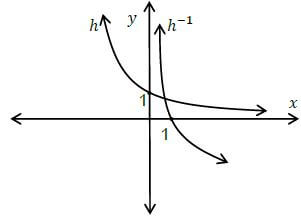? shape ? y − intercept ? point on graph	(3)

6.2	?(?) = 2^?	? answer	(1)

6.3	ℎ⁻¹? = 2^−? −? = log ? log 2 ? = − log ? / ? = − log₂ ? /? = log_½ ? log 2	? interchange ? and ? ? equation	(2)

6.4	? ≥ 0 ; ? ∈ ?		(1)

6.5	See 7.2.1	??shape and x-intercept	(2)

6.6	log1 ? = −321 −3( ) = ? 2? = 8∴ 0 < ? ≤ 8	?? = 8 ?0 < ? ≤ 8	(2)
			[11]
QUESTION 7
7.1	? = 5? = 2	?? = 5?? = 2	(2)

7.2	? = 5 − ? ? − 2 ? = −(? − 2) + 3 (? − 2) ? = 3 − 1 ? − 2	?? = 5−? ?−2 ?? = −(?−2)+3 (?−2)	(2)

7.3	?(5; 0) ? = ? − 3 ? = ? + 3 ?′(0 + 3; 5 − 3) ?′(3; 2)	?? = 3 ?? = 2	(2)
			[6]
QUESTION 8
8.1	?(?) = −2?² + ? ?′(?) = lim ?(? + ℎ) − ?(?) ℎ→0 ℎ = lim −2(? + ℎ)² + ? − (−2?² + ?) ℎ→0 ℎ = lim −2(?² + 2?ℎ + ℎ²) + ? + 2?² − ?) ℎ→0 ℎ = lim −2?² − 4?ℎ − 2ℎ² + ? + 2?² − ? ℎ→0 ℎ = lim −4?ℎ − 2ℎ² ℎ→0 ℎ = lim ℎ(−4? − 2ℎ) ℎ→0 ℎ = lim(−4? − 2ℎ) ℎ→0 = −4? Answer ONLY: 0 marks Penalise 1 mark for incorrect use of formula. Must show ?′(?)	? formula ? substitution of (? + ℎ) ? simplification to (−4?ℎ − 2ℎ²) ? common factor ? answer	(5)

8.2		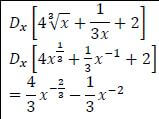	(4)
			[9]
QUESTION 9
9.1	?(?) = (? − 1)²(? + 3) ?(?) = ?³ + ?² − 5? + 3 ?′(?) = 3?² + 2? − 5 3?² + 2? − 5 = 0 (3? + 5)(? − 1) = 0 ? = − ⁵/₃ or ? = 1 ?(1) = 0 ? (− ⁵/₃ ) = 256 27	? ?(?) = ?³ + ?² − 5? + 3 ? ?′(?) = 0 ? factors ? ?-values ? ?-values	(5)

9.2		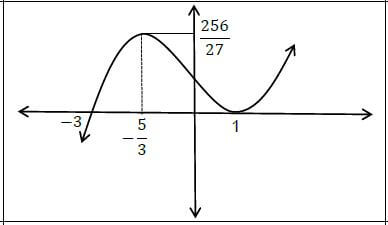? shape ? ? − intercepts ? ? − intercept ? stationary points	(4)

9.3	?′′(?) = 6? + 2 6? + 2 = 0 ? = − 1/3 ? = ¹²⁸ / ₂₇ / 4,74 / 4 ²⁰/₂₇	? f′′(?) = 6? + 2 ?? = − ¹/₃ ? ? = ¹²⁸ / ₂₇ / 4,74 / 4 ²⁰/₂₇	(3)

9.4	0 < ? < 25627	??answer	(2)

9.5	?′(?) = 3?² + 2? − 5 3?² + 2? − 5 = −5 3?² + 2? = 0 ?(3? + 2) = 0 ? = 0 or ? = − ²/₃ ? (− 2) = 175 3 27 y = −5? + ? 175 = −5 (− ²/₃ ) + ? 27 3? = 85 27 ? = −5? + 85 27	? f′(?) = −5 ? factors ? ? = − ²/₃ ? f (− ²/₃) = 175 27 ? substitution ? answer	(6)
			[20]
	QUESTION 10
10.1	243 = 2(? × 2?) + 2(2? × ℎ) + 2(? × ℎ) 243 = 4?² + 4?ℎ + 2?ℎ 243 = 4?² + 6?ℎ ℎ = 243 − 4?² 6? ℎ = 81 − 2? 2? 3	? TSA equation and sub ? simplification	(2)

10.2	? = 2? × ? × (81 − 2?) (2? 3) ? = 81? − 4 ?³ 3	?sub into volume formula	(1)

10.3	?? = 81 − 4?² ?? 81 − 4?² = 0 ?² = 81 4 ? = 9 = 4.5 2	? 81 − 4?² ? 81 − 4?² = 0 ? ?² = 81 4 ? answer	(4)
			[7]
	QUESTION 11
11.1	9 × 9 × 9 × 5 × 4 = 14580	?9 × 9 × 9 ?5 × 4 ? 14580	(3)

11.2.1	12! = 119750400 2! .2!	? 12! ?2!.2! ? 119750400	(3)

11.2.2	10! 2! = 1 = 0,015 119750400 66	?10!2! ? 119750400 ? answer	(3)
			[9]
11.3.1		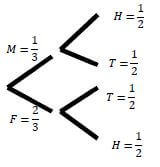? first branch with values ? top part of second branch with values ? bottom part of second branch with values	(3)

11.3.2	?(?) = 2 3	? ?(?) = ^2/₃	(1)

11.3.3	?(?/?) = 1 × 1 3 2 ?(?/?) = 1 6	? ?(?/?) = ^1/₆	(2)
			[15]
			TOTAL: 150

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Monday, 12 July 2021 07:24

GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICS
PAPER 2
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

MEMORANDUM

QUESTIONS 1

Employee	1	2	3	4	5	6	7	8	9	10
Hours in training	16	36	20	38	40	30	35	22	40	24
Productivity (units produced per day)	45	70	44	56	60	48	75	60	63	38

1.1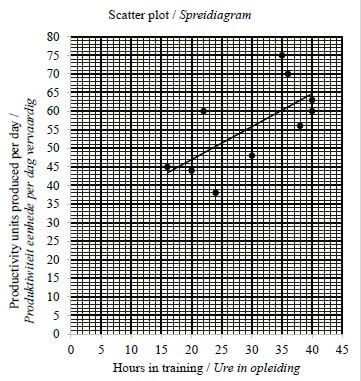

✔2-4 correct points

✔5-7 correct points

✔plotting all points

(3)

1.2

a = 29,22
b = 0,89
y = 29,22 + 0,89x

✔ A
✔ B
✔ equation

(3)

1.3

(30,9 ;55,50)
y-int 29, 22

✔ mean point (30,90;55,50 ) and y-int 29, 22
✔ regression line

(2)

1.4

y = 29,22 + 0,89(25)
= 51,47
OR
y = 51,38 [calculator use]
ANSWER ONLY FULL MARKS

✔ answer

(2)

1.5

r = 0,66

✔ answer

(1)

1.6

Moderately strong positive correlation

✔ answer

(1)

[12]

QUESTION 2

2.1

140 learners

✔ answer

(1)

2.2

60 < x £ 70

✔ answer

(1)

2.3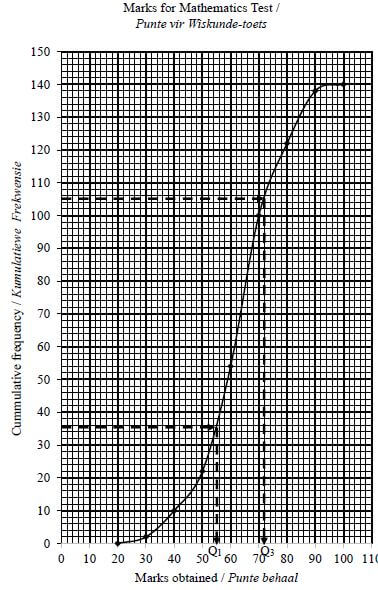

✔ grounding
✔ cummulative frequency
✔ plotting against the upper limit
✔ shape

(4)

2.3

Q₃ - Q₁ = 72 - 55
= 17

✔ Q₃ & Q₁
✔IQR

(2)

[8]

QUESTION 3

3.1

BC : x + 2 y = 14

y = - 1 x + 7
2
m_BC = m_AD = - ¹/₂y - 5 = - 1 (x + 1)
2
y = - 1 x + 9
2 2

✔ = m_AD = - ¹/₂
✔ subst. m and A into correct formula
✔ y = - 1 x + 9
2 2

(3)

3.2

- 1 x + 9 = 0
2 2
x = 9
D(9; 0)

OR

m_AD = m_BC0 - 5 = - 1
x + 1 2
- 10 = -x - 1
x = 9
D(9; 0)

✔ y = 0
✔ x = 9
✔ y = 0
✔x = 9

(2)

3.3

m_FD = 2 - 0
10 - 9
= 2
m_BC × m_FD = 2 × - 1
2
= -1
FD ⊥ BC [m_BC× m_FD = -1]

✔ correct subst.
✔ m_FD = 2
✔ m_BC× m_FD = -1

(3)

3.4

AD =√(-1 - 9)² + (5 - 0)²= √125
= 5√ 5

✔ subt. into correct formula
✔ AD = 5√ 5

(2)

3.5

FD = √(9 -10)² + (0 - 2)²= √5
A of ABCD = b × h
= 5 √5 ×√5
= 25

✔ subst. into correct formula
✔ FD = √5
✔ subst into correct formula
✔ answer

(4)

3.6

m_AB = m_DC= 6 - 5
2 - (-1)
= 1
3
∴ Inclination of DC = 18, 43º
Inclination of AD = 180º - tan^-1 [½]
= 153, 43º
ADC = 153, 43º -18, 43º
= 135º
∴ ABC = 135º [opp∠s of a parm.]

✔ subst. into correct formula
✔ m_AB = 1
3
✔ θ_DC = 18, 43º
✔ θ_AC = 153, 43º
✔ AD C = 135º
✔ ABC = 135º

(6)

[20]

QUESTION 4

4.1

x_S = 0 + 4 y_S = 0 - 6
2 2
= 2 = -3
S(2; - 3)
Answer only full marks

✔ subst. into correct formula
✔ both coordinates

4.2

SP = √(2 - 4)² + (- 3 + 6)²= √13

✔ subst. into correct formula
✔ answer

(2)

4.3

(x - 2)² + (y + 3)² = 13

✔ correct subt. centre
✔ r ² = 13.

(2)

4.4

Tangent ⊥ radius

✔ answer

(1)

4.5

m_rad = - 3 + 6
2 - 4
= - 3
2
m_tan = 2 [radius ⊥ tan]
3
y + 6 = 2 (x - 4)
3
= 2 x - 26
3 3

✔ subst. into correct form.
✔ m_rad = - 3
2
✔ m_tan = 2
3
✔ subst. into correct form

(4)

4.6

(0 - 2)² + (y + 3)² = 13
(y + 3)² = 9
y + 3 = ±3
y_T = -6
T (0; - 6)

OR

(0 - 2)² + (y + 3)² = 13
y ² + 6 y = 0
y(y + 6) = 0
y_T = -6
T (0; - 6)

OR

Draw horizontal line y = -3 with M on OT
OM = MT [⊥ from centre bisect the chord]

OM = 3
∴ MT = 3
∴ OT = 6
∴ T (0; - 6)

✔ x = 0
✔ (y + 3)² = 9
✔ y + 3 = ±3
✔ y_T = -6
✔ subs.x = 0 in eqn of circle
✔ standard form
✔ factors
✔ y_T = -6
✔ S/R
✔ length of MT
✔ length of OT
✔ answer

(4)

4.7

At U , y = - 26
3
∴TU = 26 - 6
3
= 8
3
Area ΔOTP = 1/2 × 6 × 4
Area ΔPTU 1/2 × 8/3 × 4
= 9
4

✔ U [ 0 ; -²⁶/₃]
✔ lenght of TU
✔ lenght of OT
✔ correct subst.
✔ answer

(5)

[20]

QUESTION 5

5.1.1

sin 2x = √15
8

cos2x = 2 cos² x - 1
2 cos² x = cos2x + 1
cos x = √cos2x + 1
2
= √ 7/8 + 1
2
= √15
4
OR

cos2x = 2 cos² x -1
7 = 2 cos² x -1
8
15 = cos² x
16
∴ cos x = √15
4

✔ diagram
✔ identity of cos2x
✔ cos x subject of formula
✔ cos2x = 7
8
✔ answer
✔ identity
✔ cos2x = 7
8
✔ cos² x = 15
16
✔ answer

(5)

5.2

sin(180º - θ ).sin(540º - θ ).cos(θ - 90º)
tan(- θ ).sin² (360º - θ )
= (sinθ)(sinθ ).(sinθ ).
(- tanθ )(- sinθ )²= sinθ
- sinθ
cosθ
= -cosθ

✔ sin θ
✔ sin θ
✔ sin θ
✔ (- tanθ )
✔ (- sinθ )²
✔ sinθ = tan θ
cosθ
✔ (- cosθ )

(7)

5.3.1

LHS = sin 5x. cos3x - cos5x.sin 3x -1
tan 2x
= sin(5x - 3x) -1
tan 2x
= sin 2x -1
sin 2x
cos 2x
= cos 2x -1
= 1- 2 sin ² x -1
= -2 sin ² x
∴ LHS = RHS

✔ sin (5x - 3x)
✔ tan 2x = sin 2x
cos 2x

✔ simplification
✔ identity
1- 2 sin ² x

(4)

5.3.2

tan 2x = 0
2x = 0º or 180º
x = 0º or 90º

OR

tan 2x is undefined
2x = 90º or 270º
x = 45º or 135º

✔ tan 2x = 0 / undefined
✔ 0º or 180º
✔ 90º or 270º
✔ answer

(4)

[20]

QUESTION 6

6.1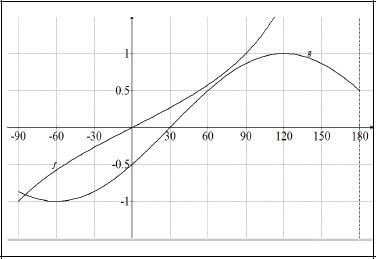

f
? both intercepts
?asymptote
?shape

g
?intercepts
?min& max values
?shape

(6)

6.2

period(e) of f(½x) = 180º
½
= 360º
Answer only full marks

? = 180º
½
? 360º

(2)

6.3

0º < x < 30º

?critical values
?notation

(2)

6.4

x = 170º

? answer

(1)

[11]

QUESTION 7

7.1

Area ΔABC = 1 .AB.BC.sinB
2
= 1 × 17 × 17 × sin105º
2
= 139,58

? Area rule formula
? correct subst.
?answer

(3)

7.2

AC ² = AB² + BC² - 2.AB.BC.cosB
= 17² + 17² - 2.17.17.cos105º

= 727,5974081
∴AC = 26,97

? cosine rule formula
? correct subst into cosine rule
? AC = 26,97

(3)

7.3

sinACD = sinD
AD AC
sinACD = sin75º
13 26,97
sinACD = 13 × sin75º
26,97
= 0,4655927231
ACD = 27,75º

? sine rule formula
? correct subst. into sine rule
? answer

(3)

7.4

Converse opp ∠ s of a cyclic quad

OR

int.opp.∠ s of a quad suppl

? reason

OR

? reason

(1)

[10]

QUESTION 8

8.1.1

S = 90º [∠ in semi - circle]

? S
? R

(2)

8.1.2

T₂ = S = 90º [corresp.∠ s RS ΙΙ Q]
∴ T is the midpt of SP         [ line from centre ⊥ to chord]
QP = 10 andTP = 8
QT² = (10)² - (8)2                     [Pyth.Theorem]
∴ QT = 6
QU = QP = 10                [radii]
∴ TU = 4

?      S/R
?      S/R
?      subst. into Pyth.
?       QT
?       S/R
?      TU

(6)

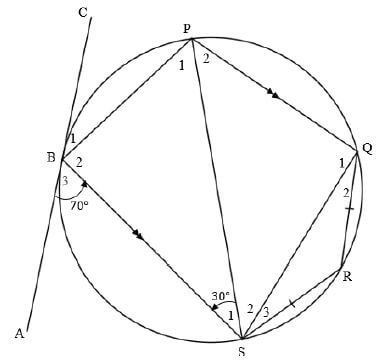8.2.1

B₁ = 30º [tan chord theorem]

?S ? R

(2)

8.2.2

P₂ = 30º [alt ∠ s, BS ΙΙ PQ]

?S ? R

(2)

8.2.3

R = 150º [opp ∠ s of a cyclic quad]

?S ? R

(2)

8.2.4

Q₂ = S₃ [∠ s opp =sides]
Q₂ = 180º -150º [sum of ∠ sin a Δ]
2
= 15º

? S/R
? S
? answer

(3)

[17]

QUESTION 9

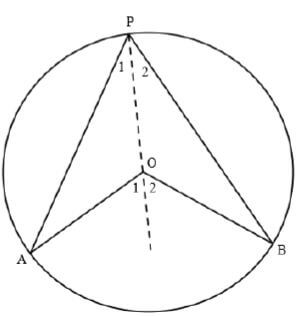9.1

O₁  = P₁ + A and O₂ = P₂ + B [ext ∠ of a Δ]
AO = OP = OB                           [radii]
P₁ = A and P₂ = B [∠ s opp =sides]
∴ O₁  = 2P₁ and O₂ = 2P₂∴O₁  + O₂ = 2P₁ + 2P₂AOB = 2 (P₁ + P₂)
= 2APB

?S/R
?S/R
?S/R
?S

(4)

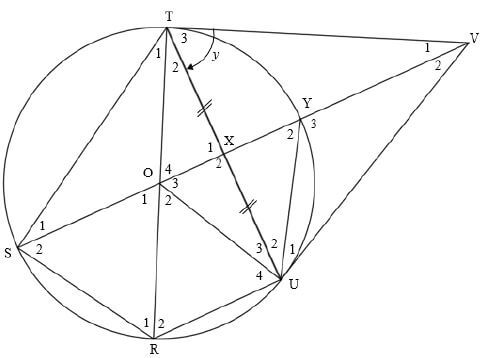9.2.1

RUT = 90º [∠ in a semi - circle]
X₁ = 90º [line from centre to midpoint]
∴RU ΙΙ SY [corresp.∠ s =]

OR

RUT = 90º [∠ in a semi - circle]
X₁ = 90º [line from centre to midpoint]
∴ RUT + X₂ = 90º + 90º = 180º
∴RU ΙΙ SY [co-int.∠ s supp]

?S         ? R
?S         ? R
? R
?S
? R
?S
? R
? R

(5)

9.2.2

R₂ = y [tan chord theorem]
= O₁ [alt ∠s, RU ΙΙ SY]
∴T₁= 1 O₁ [∠ at centre = twice ∠at circumf.]
2
= 1 y
2

?S ? R
?S ? R
? R

(5)

9.2.3

O₄ = y = O₁        [vert opp.∠ s]
TUV = y            [tan from same point =in length]
∴ TOUVis a cyclicquad            [converse same segment]

OR

VTO = 90º [tan ⊥ radius]

VUO = 90º [tan ⊥ radius]

∴VTO + VUˆ O = 180º

∴TOUVisa cyclicquad [converseoppÐsof cyclicquad.supp]

?S         ? R
?S         ? R
? R
?S         ? R
?S         ? R
? R

(5)

[19]

QUESTION 10

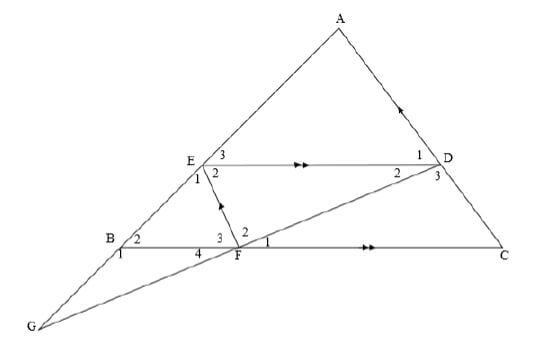10.1

BA = BC [prop theorem; EF ΙΙ AC]
EA FC
= CA [prop theorem; ED ΙΙ BC]
DA
∴BC = CA
FC DA

?S ?R
?S
?R

(4)

10.2

B₂ = E₃ [corresp ∠s : EDΙΙBC]
E₁ = A [corresp ∠s : EFΙΙAC]
∴F₃ = D1 [sum of ∠s of Δ ]
∴ΔBFE ΙΙΙ ΔEDA [∠∠∠]

?S/R
?S/R
?R

(3)

10.3.1

AD = ED [ΔBFE ΙΙΙ ΔEDA]
FE BF
AD = 10
2 3,5
AD = 40 = 5,71
7

?S
?R
? subst.
? AD

(4)

10.3.2

DC = EF = 2 [opp.sidesof a parm]

?S
?R

(2)

[13]

TOTAL : 150

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!

Monday, 12 July 2021 07:23

GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017

GRADE 12 MATHEMATICS
PAPER 2
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

INSTRUCTIONS AND INFORMATION

This question paper consists of 10 questions.
Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
Clearly show ALL calculations, diagrams graphs, et cetera which you have used in determining the answers.
Answers only will NOT necessarily be awarded full marks.
If necessary, round off your answers to TWO decimal places, unless stated otherwise
Diagrams are not necessarily drawn to scale.
You may use an approved scientific calculator (non-programmable and non-graphical) unless stated otherwise.
An information sheet with formulae is included at the end of the question paper. 9. Write neatly and legibly.

QUESTIONS

QUESTION 1
A training company wants to know if there is a link between the hours spent in training by a particular category of employee and their productivity (units produced per day). The following data was extracted from files of 10 employees.

Employee	1	2	3	4	5	6	7	8	9	10
Hours in training	16	36	20	38	40	30	35	22	40	24
Productivity (units produced per day)	45	70	44	56	60	48	75	60	63	38

1.1 Draw a scatter plot of the data on the grid provided in the ANSWER BOOK. (3)
1.2 Determine the equation of the least squares regression line. (3)
1.3 Draw the least squares regression line on the scatter plot drawn in QUESTION 1.1. (2)
1.4 Use the least squares regression line to predict the productivity (units produced per day), if a particular category of employee spent 25 hours in training. (2)
1.5 Determine the correlation coefficient of the data. (1)
1.6 Comment on the strength of relationship between the hours spent in training and the number of units produced per day. (1)

[12]

QUESTION 2
The marks obtained by learners of a certain school in a Mathematics test is represented in the histogram below: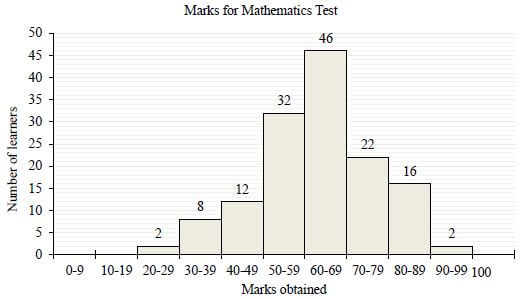

2.1 How many learners wrote the test? (1)
2.2 Write down the modal class. (1)
2.3 Draw the ogive for the given information. (4)
2.4 Use the ogive to estimate the interquartile range. (2)

[8]

QUESTION 3
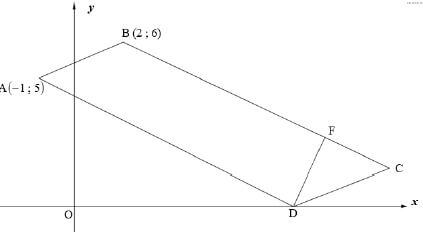
In the diagram below, A (-1 ; 5), B (2 ; 6), C and D are the vertices of parallelogram ABCD. Vertex D lies on the x-axis. The equation of BC is x + 2y = 14.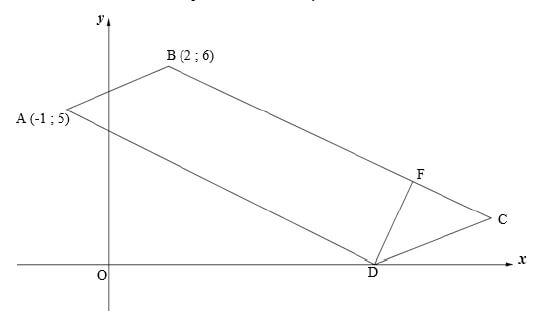

3.1 Determine the equation of line AD in the formy = mx + c. (3)
3.2 Determine the coordinates of D. (2)
3.3 If the coordinates of F are (10 ; 2), show that DF is perpendicular to BC. (3)
3.4 Calculate the length of AD. (Leave your answer in surd form.) (2)
3.5 Hence, or otherwise, calculate the area of parallelogram ABCD. (4)
3.6 Calculate the size of AB̂C. (6)

[20]

QUESTION 4

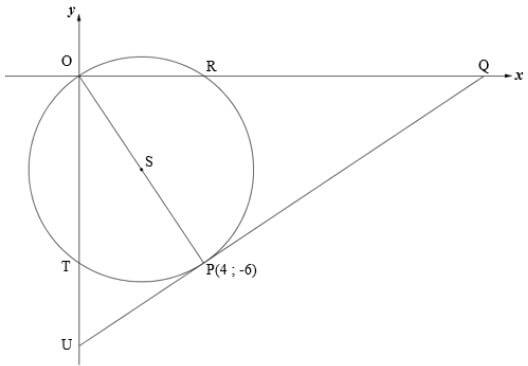
In the diagram below, the circle with centre S, passes through the origin, O, and intersects the x-axis at R and y-axis at T. The tangent to the circle at P(4 ; -6) intersects the x-axis at Q and the y-axis at U.

4.1 Calculate the coordinates of S, the centre of the circle. (2)
4.2 Calculate the length of the radius of the circle. (Leave your answer in surd form.) (2)
4.3 Determine the equation of the circle in the form of (x − a)² + (y − b)² = r². (2)
4.4 Why is QP̂U = 90°? (1)
4.5 Show that the equation of the tangent UQ is: y =²/₃x −²⁶/₃. (4)
4.6 Determine the coordinates of T. (4)
4.7 Determine the ratio of Area △OTP in its simplest form. (5)
Area △PTU

[20]

QUESTION 5

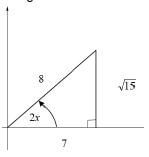
5.1 Given: sin 2x =√15 and 0° ≤ 2x ≤ 90°.
x
Determine with the aid of a diagram and without using a calculator the value of cos x. (5)
5.2 Simplify the following expression to one trigonometric ratio of θ:
sin(180° − θ) . sin(540° − θ). cos(θ − 90°)
tan(−θ). sin2(360° − θ) (7)
5.3 Given the identity: sin 5x.cos 3x.−cos 5x .sin3x − 1 = −2 sin²x.
tan 2x

5.3.1 Prove the above identity. (4)
5.3.2 For which value(s) of x will the above identity be undefined for 0° ≤ x ≤ 180°. (4)

[20]

QUESTION 6
Given f(x) = tan ¹/₂x and g(x) = sin(x − 30°) for x ∈ [−90°; 180°]
6.1 On the same set of axes draw the graphs of f and g. Show clearly on your graphs the turning points and asymptotes, if any. (6)
6.2 Write down the period of f. (2)
6.3 For what values of x is f(x). g(x) < 0 for x ∈ [−90°; 120°]? (2)
6.4 Write down the equation(s) of the asymptotes of h if ℎ(x) = f(x + 10°) for x ∈ [−90°; 180°] (1)

[11]

QUESTION 7
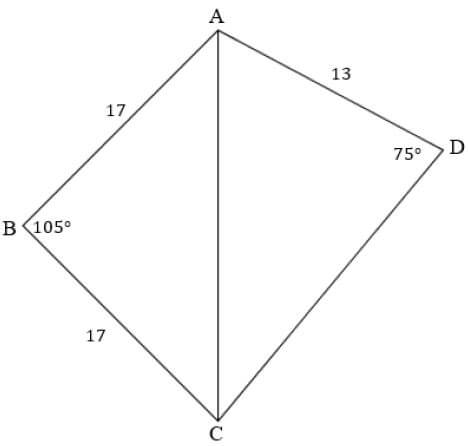
In the diagram below, ABCD is a quadrilateral with diagonal AC drawn.
AB = BC = 17 m
AD = 13 m
D̂ = 75°
B̂ = 105°

Calculate:

7.1 The area of △ ABC. (3)
7.2 The length of AC. (3)
7.3 The size of AĈD. (3)
7.4 Give a reason why ABCD is a cyclic quadrilateral. (1)

[10]

Give reasons for ALL statements in QUESTION 8, 9, 10 AND 11.
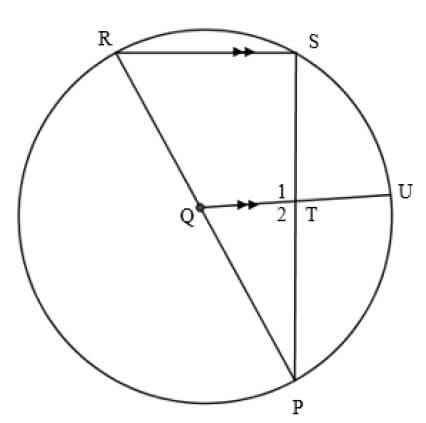
QUESTION 8
8.1 PR is a diameter of the circle PRSU. QU is drawn parallel to RS and meets SP in T.

8.1.1 Write down, with a reason, the size of Ŝ. (2)
8.1.2 If the diameter is 20 cm and SP = 16 cm, calculate the length of TU. (6)

8.2 ABC is a tangent to circle BPQRS at B. PQ ∥ BS. QR = RS. Ŝ1 = 30° and B̂3 = 70°.

Calculate, with reasons, the size of the following angles:

8.2.1 B̂₁(2)
8.2.2 P̂₂(2)
8.2.3 R̂ (2)
8.2.4 Q̂₂(3)

[17]

QUESTION 9
9.1 A, B and P are the points on the circle with centre O. AO, BO, AP and BP are drawn.

Prove the theorem which states that AÔB = 2AP̂B. (4)
9.2 TV and VU are tangents to the circle with centre O at T and U respectively. TSRUY are points on the circle such that RT is the diameter. X is the midpoint of chord TU. T̂₃ = y.

Prove that:

9.2.1 RU ∥ SY (5)
9.2.2 T̂₁=½y (5)
9.2.3 TOUV is a cyclic quadrilateral (5)

[19]

QUESTION 10
In the diagram below, D and E are points on sides AC and AB respectively of △ ABC such that DE ∥ BC. F is a point on BC such that EF ∥ AC. AB produced and DF produced meet in G.

10.1 Prove that: BC = AC
FC DA(4)
10.2 Prove that: Δ BFE ||| Δ EDA(3)
10.3 It is further given that EF = 2, BF = 3,5 and ED = 10, determine the length of:

10.3.1 AD (4)
10.3.2 DC (2)

[13]
TOTAL: 150

Published in 2017 September Grade 12 Trial Examinations

Tagged under

Be the first to comment!