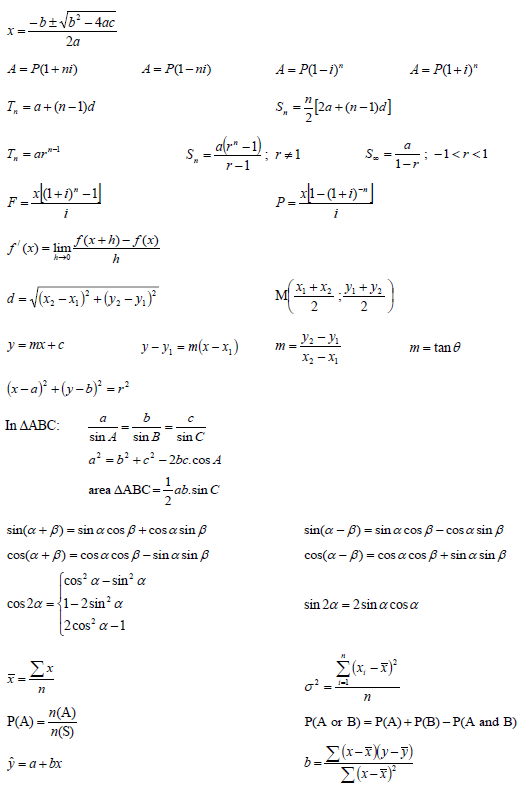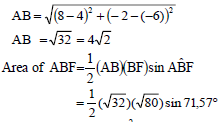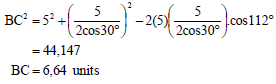Adele
Mechanical Technology: Welding and Metalwork Memorandum - Grade 12 September 2021 Preparatory Exams
MEMORANDUM
SECTION A: COMPULSORY
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
1.1 C
1.2 D
1.3 D
1.4 A
1.5 B
1.6 B (6 x 1) [6]
QUESTION 2: SAFETY (GENERIC)
2.1 Safety precautions
- Pressure gauges must be checked and tested regularly and adjusted or replaced if any malfunctioning occurs.
- Supporting pins that keep the platform at a desired height on the frame must be inspected for damage.
- Check the floor for oil and apparatus for leaks.
- The platform on which the workpiece rests must be rigid and square with the press cylinder. (Any 2 x 1) (2)
2.2 Product Layout![]() (2)
(2)
2.3 Perspex shield is installed to shield flying objects hurting the operator’s eye. (1)
2.4
2.4.1 Identification of machine Surface grinder (1)
2.4.2 Labels for parts of a surface grinder
- – Workpiece
- – Machine spindle
- – Magnetic table
- – Grinding wheel (4 x 1) (4)
[10]
QUESTION 3: MATERIALS (GENERICS)
3.1 Heat treatment refers to heating and cooling of metals under controlled conditions in their solid state so as to change their properties. (2)
3.2 HEAT TREATMENT PROCESS
PROCESS | PROPERTY | |
3.2.1 | Hardening | Very hard, maximum tensile and brittle |
3.2.2 | Tempering | Ductile |
3.2.3 | Annealing | Soft and ductile. |
3.2.4 | Normalising | Tough and machinable. |
(4 x 1) (4)
3.3 Purpose for case hardening:
- It hardens the surface.
- It provides a wear resistant surface.
- Strengthens core to withstand applied loads. (Any 2 x 1) (2)
3.4 Carbon effect:
- Steel with low carbon content will not respond very much to the hardening process. (2)
3.5
- Sound test workshop test on materials
- Bend test
- Filling test
- Machining test (Any 2 x 1) (2)
3.6 Reasons for annealing:
- To relieve internal stresses that may have been set up during other processes.
- To soften them to facilitate the machining processes.
- To make material ductile.
- Refine their grain structures.
- Reduce brittleness. (Any 2 x 1) (2)
[14]
QUESTION 4 MULTIPLE-CHOICE QUESTIONS (SPECIFIC)
4.1 D
4.2 C
4.3 B
4.4 D
4.5 A
4.6 C
4.7 B
4.8 B
4.9 A
4.10 B
4.11 D
4.12 D
4.13 B
4.14 D (14 x 1) [14]
QUESTION 5: MATERIALS TEMPLATES – ROLLING AND BENDING
5.1 Purpose of purlins in roof trusses:
- Purlins are fastened to the roof trusses to attach the roof covering. (2)
5.2 Reason why stiffeners are used in beams.
- To strengthen the web of the beam. (1)
5.3 The use of strip templates:
- They are used for longer sections of angle iron to mark off holes to be drilled. (1)
5.4 What does templates indicate?
- The correct form and measurements of the project
- The type of material to be used. (thickness and size)
- Job number
- Drawing number
- The number of components required
- This side up or other side up markings
- Coloured or shaped markings to denote hole diameters (Any 2 x 1) (2)
5.5 Labels of roof truss:
- A – Purlin
- B – Rafter
- C – Tie beam
- D – Shoe plate
- E – Inclined toe (5 x 1) (5)
5.6 Sketches:
5.6.1 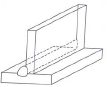 (3)
(3)
5.6.2  (3)
(3)
5.7 Calculations:
- Mean diameter = 220 + 220 + 12 ÷ 2
= 452 ÷ 2
= 226 mm (2) - Circumference = 3,142 x 226 mm
= 710,09 mm (1) - Length required for 2 straight pieces = 66 mm + 66 mm
= 132 mm - Length of material for 1 clamp = 710,09 mm + 132 mm
= 842,309 mm - Length of material for 20 clamps = 842,309 mm x 20
= 16 841 mm (3)
[23]
QUESTION 6: TOOLS
6.1 TWO different types of tap wrenches:
- T-handle or double handle OR
- Adjustable wrenches (2)
6.2 Uses of bench grinders:
- Grinding off excess material
- Cleaning surfaces with a wire wheel
- Polishing or buffing (Any 2 x 1) (2)
6.3 Purpose of a powersaw:
- It is used to rough cut large sections of metal. (1)
6.4 Determine the drilling speed of a pedestal drilling machine:
- Slower speed – for large diameters
- Faster speed – for small diameter holes. (2)
6.5 Reasons why guillotines have material thickness cutting limits:
- To preserve the shearing blades.
- Thicker or harder material will chip the brittle blade and result in poor future cuts or jamming of the guillotine. (2)
6.6 Sketch of basic AC arc welding machine: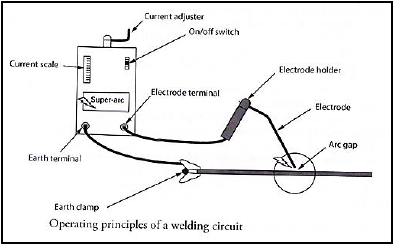
(Any 7 labels x 1) (7)
6.7 The use of shielding gas in MIG welding:
- MIG welding machines use a shielding gas to protect the weld pool from atmospheric gases. (2)
[18]
QUESTION 7: FORCES
7.1
7.1.1 Stress
- This is an internal force in material resisting a load. (2)
7.1.2 Strain
- This is the measurement of the deformation produced by the external forces and is determined by the ratio between deformation and original length. (2)
7.1.3 Safety factor
- This is the maximum number of times with which the maximum stress is decreased to obtain a safe stress. (2)
7.2
7.2.1 The stress in the material:
- Stress = Load
Area
but Area = πd2
4
= π × (0,05)2
4
1,964 × 10-3 m2
Stress = 50 × 103
1,964 × 10-3
= 25,46 × 106 Pa
= 25,46MPa (4)
7.2.2 The strain if the final length of the bar is 3,00 m.
- Strain = ΔL
OL
but
Final length = OL + ΔL
ΔL = final length - OL
= 3,005 - 3
= 0,005 m
Strain = 0,005
3
= 1,67 ×10-3 (3)
7.3 Labelled sketch of the stress strain graph.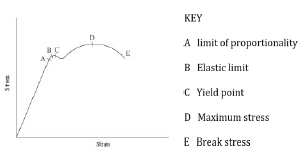
(Each label x 1) (7)
7.4
7.4.1 Calculate the reactions at the supports LR and RR
CALCULATING REACTIONS
- Take moments about RR
LR x 13 = (50 x 5 x 10,5) + (400 x 8) + (600 x 3)
= 2 625 + 3 200 + 1 800
LR = 586,5 N - Take moments about LR
RR x 13 = (600 x 10) + (400 x 5) + (50 x 5 x 2,5)
= 6000 + 2000 + 625
RR = 663,5 N (6)
7.4.2 Calculate the BM at each point of the beam A, B, C and D.
- BENDING MOMENTS
BMA: = 586,5 x 0 = 0 Nm
BMB: = (586,5 x 5) – (250 x 2,5) = 2307,5 Nm
BMC: = (586,5 x 10) – (250 x 7,5) – (400 x 5) = 1 990 Nm
BMD: = (586,5 x 13) – (250 x 10,5) – (400 x 8) – (600 x 3) = 0 m (4)
7.4.3 Calculate the shear force at A, B, C and D.
- SHEAR FORCE SFA: 586,5 N
SFB: 586,5 – 250 = 336,5 N
SFC: 586,5 – 250 – 400 = -64,5 N
SFD: 586,5 – 250 – 400 – 600 = -663,5 N (4)
7.5 Vector diagram: Scale 10 mm = 1 N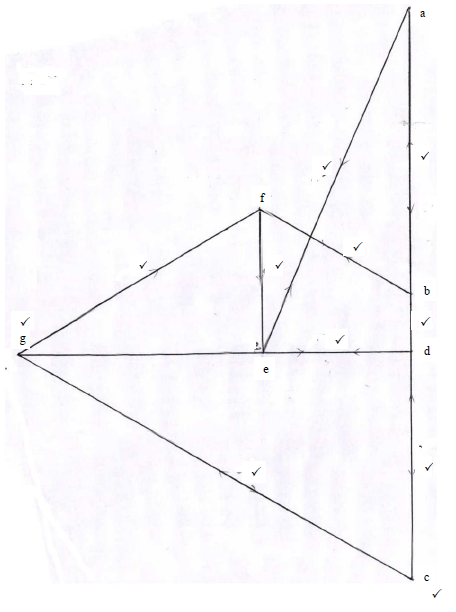
(11) [45]
QUESTION 8: JOINING METHODS (INSPECTION OF WELDS)
8.1 Internal defects – Nickbreak test:
- Slag inclusion
- Porosity
- Lack of fusion
- Oxidised metal
- Burned metal (Any 3 x 1) (3)
8.2 Visual requirements for an acceptable weld:
- Shape of the profile
- Uniformity of the surface
- Overlap
- Free from any external defects
- Penetration bead
- Root groove (Any 3 x 1) (3)
8.3 Elements during the visual inspection in welding:
- Shape of profile
- Uniformity of the surface
- Overlap
- Undercutting
- Penetration bead
- Root groove (Any 3 x 1) (3)
8.4 Performing an X-ray test on a welded joint:
- The X-ray or gamma ray source is placed in front of the object being tested.
- Once the tester is standing behind lead shields and far away from possible harmful exposure, the source is activated for a brief moment and the
X-rays penetrate the test piece. - As they pass through the areas of lower density (air pockets, cracks or inclusions) the rays expose the film as lighter on the negative, indicating a welding defect.
- Photographic films are useful because they provide a permanent record of the shadow which can be carefully studied. (5)
8.5 Factors that determine the current setting in arc welding.
- Base metal type
- Base metal thickness
- Electrode thickness (3 x 1) (3)
8.6 Factors that should be considered during oxyacetylene welding to ensure quality welding:
- Correct flame for the work at hand
- Correct angle of welding torch and rod
- Depth of fusion
- The welding rate (Any 3 x 1) (3)
8.7 Preventative measures for porosity during MIG welding:
- Cleaning the welding surface.
- Avoid rust in MIG wire electrode.
- Ensure that supply of shielding gas is not interrupted.
- Avoid welding in windy condition. (Any 3 x 1) (3)
[23]
QUESTION 9: JOINING METHODS (STRESSES AND DISTORTION)
9.1 Methods used to reduce distortion:
- Do not over-weld
- Apply intermittent welding
- Place welds near the neutral axis
- Use as few passes as possible
- Use back-step welding
- Anticipate the shrinkage forces
- Plan the welding sequence
- Use strongbacks
- Use clamps, jigs and fixtures (Any 5 x 1) (5)
9.2 Distortion on a welded joint:
- Weld distortion is the warping of the base plate caused by heat from the welding arc/flame. (2)
9.3 The meaning of shrinkage in a welded joint:
- Shrinkage is a form of plastic deformation where the metal has deformed because of contraction on cooling. (2)
9.4 The iron-carbon equilibrium diagram labels:
- – Ferrite and pearlite
- – Ferrite and austenite
- – Austenite
- – Cementite and austenite
- – Pearlite and cementite (5)
9.5 The factors that affect the grain size of steel when it is being cold worked:
- The prior amount of cold work.
- The temperature and time of the annealing process.
- The composition
- The melting point (4)
[18]
QUESTION 10: MAINTENANCE
10.1 Tagging plates have multiple holes:
- It has multiple holes so that more than one technician can lock out the machine simultaneously. (2)
10.2 General maintenance guidelines for a pedestal drilling machine :
- Visual checks of electrical wiring, switches, etc.
- Verify that all guards are secure and function correctly
- Ensure workspace is clear and without hindrances.
- Confirm availability and conditions of PPE
- Lubricate moving parts.
- Use moisture-penetrating oil spray to prevent rust.
- Check the availability of specific tools.
- Check the run-out of the spindle.
- Inspect belts for wear and tear.
- Ensure the drive belt is correctly tensioned.
- Check the condition of the rack and pinion mechanisms and lubricate.
- Ensure cuttings are removed.
- Inspect the Morse taper sleeves for burrs/scratches. (Any 2 x 1) (2)
10.3 Reasons for the maintenance of machines in the welding workshop:
- Promote cost saving.
- Improves safety.
- Increases equipment efficiency.
- Fewer equipment failure.
- Improves reliability of equipment. (Any 2 x 1) (2)
10.4 Methods to reduce friction when drilling holes:
- By reducing both drill speed and feed speed.
- By applying lubrication. (cutting fluid) (2)
[8]
QUESTION 11: TERMINOLOGY (DEVELOPMENT)
Calculations:
11.1
- 1 – 2 = ?? ?
12
= 3.142 × 72
12
1 – 2 = 18,849
1 – 2 = 2 – 3 = 3 – 4 = 18,849 (4)
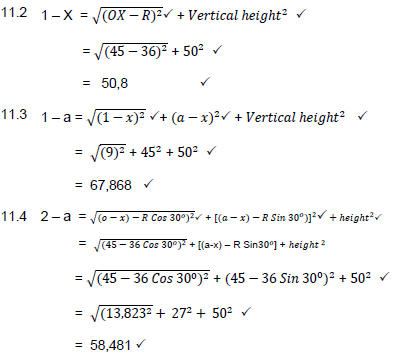
11.5
- a – x = 90 ÷ 2
= 45 (2)
[21]
TOTAL: 200
Mechanical Technology: Welding and Metalwork Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
- Write your NAME and SURNAME on the ANSWER BOOK.
- Read ALL the questions carefully.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- Show ALL calculations and units. Round off final answers to TWO decimal places.
- Candidates may use non-programmable scientific calculators and drawing instruments.
- The value of gravitational force should be taken as 10 m.s-2.
- All dimensions are in millimetres, unless stated otherwise in the question.
- A formula sheet is attached to the question paper.
- Write neatly and legibly.
- Use the criteria below to assist you in managing your time.
QUESTION | CONTENT | MARKS | TIME IN MINUTES |
GENERIC | |||
1 | Multiple-choice questions | 6 | 6 |
2 | Safety | 10 | 10 |
3 | Materials | 14 | 14 |
SPECIFIC | |||
4 | Multiple choice questions | 14 | 10 |
5 | Terminology (Templates – rolling and bending) | 23 | 20 |
6 | Tools and Equipment | 18 | 20 |
7 | Forces | 45 | 30 |
8 | Joining methods (Inspection of welds) | 23 | 20 |
9 | Joining methods (Stresses and distortion) | 18 | 20 |
10 | Maintenance | 8 | 10 |
11 | Terminology (Specific) | 21 | 20 |
TOTAL: | 200 | 180 | |
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS (GENERIC) (COMPULSORY)
Various options are provided as possible answers to the following questions. Choose the correct answer and write only the letter (A–D) next to the question numbers (1.1–1.6) in the ANSWER BOOK, for example 1.7 A.
1.1 Which ONE of the following safety procedures is applicable to the maintenance/operation of a hydraulic press?
- Do not apply a wrench to revolving work.
- Guards could be removed when pressing soft material.
- Pressure gauges must be tested regularly and adjusted or replaced if any malfunctioning occurs.
- Use the machine table as an anvil. (1)
1.2 What is the best way of dealing with a hazard to ensure others are not put at risk?
- Remove it immediately
- Leave it for the supervisor to sort out
- Not placing a barrier tape around it
- Display a notice or warning sign (1)
1.3 Which of the following is a safety precaution related to a workbench?
- The tool rest must not be more than 3 mm from the grinding wheel.
- Make sure the chuck is correctly tightened.
- Stand on the side when switching on the machine.
- Keep rolling stock or items away from the bench end. (1)
1.4 What is the colour of an acetylene cylinder?
- Maroon
- Grey
- Green
- Black (1)
1.5 Starting devices on machinery are normally … in colour.
- red
- green
- black
- orange (1)
1.6 ONE of the following is NOT a safety device used in conjunction with guillotines.
- Self-adjusting guard
- Current scale
- Automatic sweep-away
- Electronic presence detection sensor (1)
[6]
QUESTION 2: SAFETY (GENERIC)
2.1 State TWO safety precautions that should be observed before pressing a bearing from a shaft using a hydraulic press. (2)
2.2 Sketch and label a product layout. (2)
2.3 What is the reason for mounting a Perspex shield on a bench grinding machine? (1)
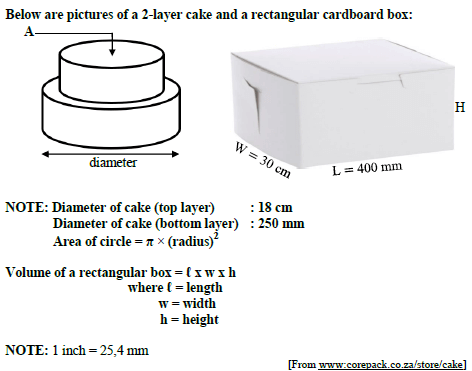
2.4 Study both pictures in FIGURE 2.4 and answer the questions that follow.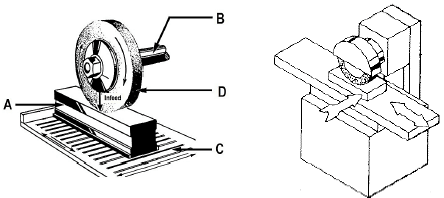
FIGURE 2.4
2.4.1 Name the machine shown in FIGURE 2.4. (1)
2.4.2 Identify the parts labelled A to D. (4)
[10]
QUESTION 3: MATERIALS (GENERIC)
3.1 Explain the term heat treatment. (2)
3.2 Tabulate the following heat PROPERTY of each. treatment processes and identify ONE PROPERTY of each.
| PROCESS | PROPERTY |
| 3.2.1 Hardening | |
| 3.2.2 Tempering | |
| 3.2.3 Annealing | |
| 3.2.4 Normalising |
(4 x 1) (4)
3.3 Describe the specific purpose for case-hardening mild steel. (2)
3.4 What effect does carbon have when hardening steel? (2)
3.5 Name TWO workshop tests which are used to make a distinction between materials. (2)
3.6 State TWO reasons for annealing as a heat-treatment process. (2)
[14]
QUESTION 4: MULTIPLE-CHOICE QUESTIONS (SPECIFIC)
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (4.1–4.14) in the ANSWER BOOK, for example 4.15 E.
4.1 Which ONE of the following statements is a basic rule for the safe handling of a press machine?
- Use a hammer to get the workpiece into position.
- The safety guard must be in place before you can start the press machine.
- Never leave the machine running if it is unattended.
- The safe working pressure must never be exceeded. (1)
4.2 Template makers have their own hand tools, such as …
- spanners.
- micrometres.
- chalk line and reel.
- sockets. (1)
4.3 What is a plate girder?
- Hollow tubing welded together.
- Combination of plates and angle iron welded together.
- Retro grids welded together.
- Combination of plates and round bars welded together. (1)
4.4 All symbols that appear above the reference line refer to welding to be done on … of the joint to which the arrow head is pointing.
- this side
- the right-side
- the left-side
- the other side (1)
4.5 Supplementary symbols indicate … information about a weld.
- additional
- calculated
- difficult
- easy (1)
4.6 The pitch is the distance from a reference point on the thread to a corresponding point on the thread ahead of it, measuring parallel as to the
… of the shaft.
- root
- crest
- axis
- screw (1)
4.7 A die is used for cutting or forming external threads on round bars and …
- square tubing.
- shafts.
- plates.
- angle iron. (1)
4.8 Arc welding is a type of welding that uses a welding supply to create an electric arc between an …
- earth terminal and electrode.
- electrode and base metal.
- electrode and electrode terminal.
- base metal and earth terminal. (1)
4.9 What is the function of spot welding?
- It is very quick and easy.
- It is safe.
- It converts AC to DC.
- The electrical resistance is very low. (1)
4.10 What is the individual members of steel frameworks such as roof trusses called that make up the structure to support the frame structure?
- Columns
- Struts and ties
- Rafters
- Purlins (1)
4.11 A UDL is a load that is spread over a certain distance. Give the meaning of UDL.
- Uniformly decreased load
- Uniformly deliberate load
- Uniformly disinclined load
- Uniformly distributed load (1)
4.12 Which of the following steps should be followed during oxy-acetylene welding?
- Correct flame for the work at hand.
- Correct angle of the blow torch and rod.
- The rate of progress along the joint.
- All of the above. (1)
4.13 What is the most common cause of heat-affected zone (HAZ) cracks in a weld?
- Excessive oxygen
- Excess hydrogen
- Excess carbon.
- Excess nitrogen. (1)
4.14 How can friction be reduced when drilling holes?
- Reduce feed speed.
- Reduce drill speed.
- Apply lubrication.
- All of the above. (1)
[14]
QUESTION 5: TERMINOLOGY (TEMPLATES – ROLLING AND BENDING)
5.1 What is the purpose of purlins in roof trusses? (2)
5.2 Give ONE reason why stiffeners are used in beams. (1)
5.3 What is the use of strip templates? (1)
5.4 What does templates indicate? (2)
5.5 FIGURE 5.5 below shows the shoe of a steel roof truss. Label the components (A–E), as indicated on the drawing. (5)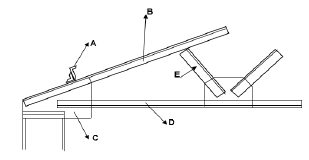
FIGURE 5.5
5.6 Sketch the welding joints that the following weld symbols represent.
5.6.1 ![]() (3)
(3)
5.6.2  (3)
(3)
5.7 FIGURE 5.7 shows a pipe clamp. The flat bar of 75 mm wide and 12 mm thick is used to form 40 clamps. Calculate the length of material required to manufacture 20 clamps.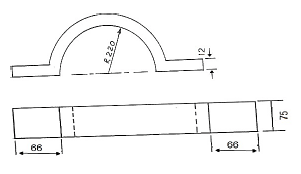 (6)
(6)
[23]
QUESTION 6: TOOLS AND EQUIPMENT
6.1 Name TWO different types of tap wrenches used in the welding workshop. (2)
6.2 What is the main uses of bench grinders in a workshop? (2)
6.3 State the purpose of a powersaw. (1)
6.4 How would you determine the drilling speed of a pedestal drilling machine? (2)
6.5 Give TWO reasons why guillotines have material thickness cutting limits. (2)
6.6 With the aid of a line diagram, SKETCH the basic operational principles of a AC arc welding machine, indicating the welding circuit. (7)
6.7 Why is shielding gas used in MIG welding? (2)
[18]
QUESTION 7: FORCES
7.1 Define the following terms:
7.1.1 Stress (2)
7.1.2 Strain (2)
7.1.3 Safety factor (2)
7.2 A tensile force of 50 kN is exerted onto a round bar with a diameter of 50 mm and an original length of 3 m. Determine by means of calculations:
7.2.1 The stress in the material (4)
7.2.2 The strain if the final length of the bar is 3,005 (3)
7.3 Make a neat, labelled sketch to show the stress strain graph. (7)
7.4 The FIGURE 7.4 below shows a uniform beam that is been supported by two vertical supports LR and RR.
Two vertical point loads are exerted onto the beam, as well as a uniformly distributed load of 50 N/m, over the total left half of the beam.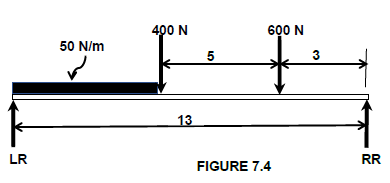
FIGURE 7.4
7.4.1 Calculate the reactions at the supports LR and RR. (6)
7.4.2 Calculate the BM at each point of the beam A, B, C and D. (4)
7.4.3 Calculate the shear force at A, B, C and D. (4)
7.5 FIGURE 7.5 below, show a framework with two vertical loads of 10 Kn each.
HINT: Copy and draw the space diagram as shown.
Determine GRAPHICALLY the nature of the forces by means of completing the force diagram.
Scale: 10 mm = 1 kN
2 m = 20 mm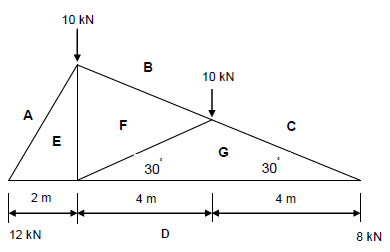 (11)
(11)
[45]
QUESTION 8: JOINING METHODS (INSPECTION OF WELDS)
8.1 Name THREE internal defects that may be detected when conducting a nickbreak test on a welded joint. (3)
8.2 State THREE visual requirements for an acceptable weld. (3)
8.3 Name THREE elements that should be inspected during the visual inspection of an arc welded joint. (3)
8.4 Describe the steps to be followed when performing an X-ray test on a welded joint. (5)
8.5 Name the factors that determine the current setting in arc welding. (3)
8.6 State THREE factors that should be considered during oxy-acetylene welding to ensure quality welding. (3)
8.7 State THREE preventative measures for porosity during MIG welding. (3)
[23]
QUESTION 9: JOINING METHODS (STRESSES AND DISTORTION)
9.1 State FIVE methods used to reduce distortion. (5)
9.2 What is distortion on a welded joint? (2)
9.3 Describe the meaning of shrinkage in a welded joint. (2)
9.4 The figure below shows the iron-carbon equilibrium diagram. Label the structures according to the letters (A–E).(5)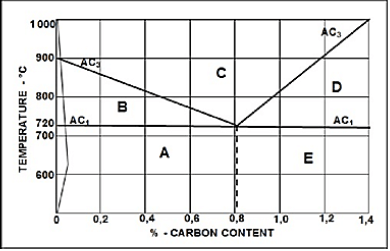
9.5 Name the factors that affect the grain size of steel when it is being cold worked. (4)
[18]
QUESTION 10: MAINTENANCE
10.1 Why do tagging plates have multiple holes? (2)
10.2 State TWO general maintenance guidelines for a pedestal drilling machine. (2)
10.3 Give TWO reasons for the maintenance of machines in the welding workshop. (2)
10.4 Name TWO methods to reduce friction when drilling holes. (2)
[8]
QUESTION 11: TERMINOLOGY (SPECIFIC)
Calculate the following true lengths on the hopper shown below:
11.1 Calculate the true length of 1 – 2, 2 – 3, 3 – 4. (4)
11.2 Calculate the true length of 1 – x. (4)
11.3 Calculate the true length of 1 – a. (5)
11.4 Calculate the true length of 2 – a. (6)
11.5 Calculate the length of a – x.
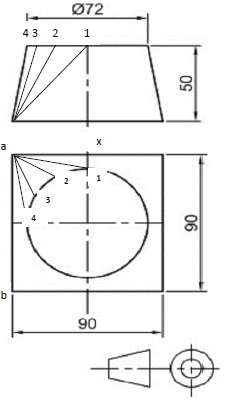 (2)
(2)
[21]
TOTAL: 200
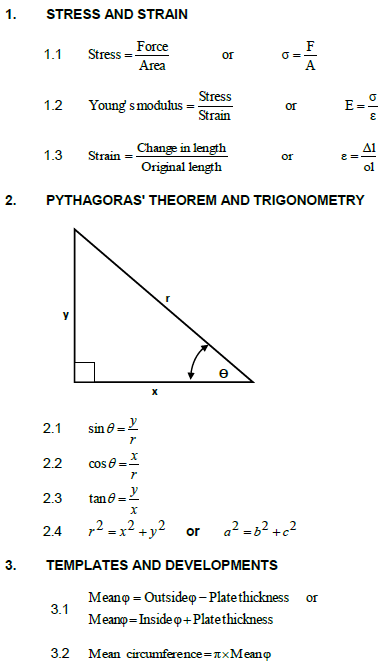
FORMULA SHEET FOR MECHANICAL TECHNOLOGY (WELDING AND METALWORK)
Mathematical Literacy Paper 2 Memorandum - Grade 12 September 2021 Preparatory Exams
Symbol | Explanation |
M | Method |
MA | Method with accuracy |
CA | Consistent accuracy |
RCA | Rounding consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
SF | Correct substitution in a formula |
J | Justification |
O | Opinion/Example/Definition/Explanation/Justification/Verification |
RT/RG/RM | Reading from a table/graph/map |
P | Penalty, e.g. for no units, incorrect rounding off etc. |
R | Rounding off |
NPR | No penalty rounding or omitting units |
AO | Answer only, full marks |
MARKING GUIDELINES
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- If a candidate has crossed out (cancelled) an attempt to a question and NOT redone the solution, mark the crossed out (cancelled version)
- Consistent Accuracy (CA) applies in ALL aspects of the marking guidelines; however, it stops at the second calculation error.
- If the candidate presents any extra solution when reading from a graph, table, layout plan and map, then penalise for every extra incorrect item presented.
MEMORANDUM
KEY TO TOPIC SYMBOL: | ||||||
QUESTION 1 [26 MARKS] | ||||||
Quest | Solution | Explanation | Level | |||
1.1.1 | 25 mg : 1 000 mg √M (divide by 25)
| 1M ratio concept | M | |||
1.1.2 | Tablets per day: Tablets per week: | 1MA multiplying by 2 | M | |||
1.1.3 | Number of days to use tablets: | 1M finding the number of days | M | |||
1.1.4 | 25 mg × 120 √RT = 3 000 mg ÷ 1 000 √C = 3 g √A | 1RT multiply correct values | M | |||
1.2.1 | The “North Elevation” shows the side view of the building from the northern direction. √√A | 2A correct explanation. (2) | MP | |||
1.2.2 | (a) | A floor plan shows a top view of the inside of a building. √√A | 2A correct explanation (2) | MP L1 | ||
(b) | An elevation plan shows the side view of the outside of the building. √√A | 2A correct explanation (2) | MP L1 | |||
1.2.3 | Scale = 1 : 100 | 1M multiply by scale | MP | |||
1.3.1 | 90 km × 1000 × 100 × 10 √C OR √C | 1C multiply by 1000 000 1A correct answer (2) | M | |||
1.3.2 | No of tiles per box = 1,44 ?2 √M | 1M dividing by 0,36 ?2 | M | |||
1.3.3 | 1,125 hours | 1C finding minutes 1C finding seconds | M | |||
[26] | ||||||
QUESTION 2 [28 MARKS] | |||||
Quest | Solution | Explanation | Level | ||
2.1.1 | George; Knysna; Mossel Bay √√RT | 2RT names of towns (2) | MP | ||
2.1.2 | South East √ √A (accept East) | 2A Direction | MP | ||
2.1.3 | National roads connect major cities. √√O | 2O Reason 1 | MP | ||
2.1.4 | 2,3 cm = 300 km √A | 1A measured bar scale | MP L2 | ||
2.1.5 | Distance = Speed × Time | Accept CA from Q 2.1.4 | MP L4 | ||
Quest | Solution | Explanation | Level |
2.2.1 | 7,6 litres = 100 km | Accept CA from Q 2.1.4 | MP |
2.2.2 | 1 642 cents ÷ 100 = R16,42 √M | Accept CA from Q 2.2.1 | MP |
[28] |
QUESTION 3 [34 MARKS] | ||||
Quest | Solution | Explanation | Level | |
3.1.1 | Radius: 18 cm ÷ 2 = 9 cm √M | 1M radius | M | |
3.1.2 | Radius: 250 mm ÷ 2 = 125 mm √MA OR Radius: 250 mm ÷ 2 = 125 mm √MA | 1MA finding radius OR 1MA finding radius | M | |
3.1.3 | Conversion: length = 400 mm ÷ 10 = 40 cm √C | 1C conversion | M | |
3.1.4 | 25,4 mm = 1 inches | 1RT using correct values 250 mm and 25,4 | M | |
3.1.5 | Radius value | 1MA finding the radius | M | |
3.1.6 | Flour : Sugar (3 cups) OR 7 √MA × 6 √MA = 14 cups of flour √A | 1MA dividing by 3 1MA multiplying by 7 | M | |
Quest | Solution | Explanation | Level | |
3.1.7 | °C = (°F – 32°) ÷ 1,8 SF | 1SF correct value | M | |
3.2.1 | Tree diagram √√A | 2A correct answer (2) | P | |
3.2.2 | Missing value P: Boy √RT | 1RT correct answer | P | |
3.2.3 | (a) | Probability (2 girls at least) = 4/8 √RT√RT | 1RT Numerator | P |
3.2.3 | (b) | Probability (BGB) = 0 % √√A | 2A correct percentage (2) | P |
[34] | ||||
QUESTION 4 [32 MARKS] | |||
Quest | Solution | Explanation | Level |
4.1.1 | Basin / Wash basin √√RT | 2RT correct feature (2) | MP |
4.1.2 | 1 Window √√RT | 2RT correct number (2) | MP |
4.1.3 | Width (bedroom 1 and bedroom 2) = 4 680 + 5 130 √MA Length of bathroom = 13 680 – 9810 √ M Wall (minus door opening) = (3 870 – 860) mm √ M | 1MA adding correct values | M |
| 4.2.1 | Bathroom Area = Length × Width = 3 870 mm × 2 250 mm √SF √A = 8 707 500 mm2 ÷ 1 000 000 √C = 8,7075 m2 √ CA Kitchen Area = Length × Width √SF = 6 030 mm × 5 130 mm √A = 30 933 900 mm2 ÷ 1 000 000 √ C = 30,9339 m2 √CA Total Area = 8,7075 + 30,9339 = 39,6414 m2 √CA | 1SF correct values 1A finding area 1SF correct values | M L3 | |
4.2.2 | Area of 1 tile: 500 mm × 500 mm | CA from 4.2.1 | M | |
4.2.3 | No of boxes = 167 ÷ 4 √MCA | CA tiles from 4.2.2 | M | |
[32] | ||||
QUESTION 5 [30 MARKS] | |||
Quest | Solution | Explanation | Leve l |
5.1.1 | Convert: 175 ÷ 100 = 1,75 m √C | 1C conversion | M |
5.1.2 | Overweight √√ J | 1J conclusion (2) | M |
5.1.3 | The young promising rugby player can eat healthier. √√O | 2O Explanation (2) | M |
5.2.1 | 3 laps = 5 000 m ÷ 1000 √C | 1C divide by 1 000 | MP |
5.2.2 | Incomplete runs: = 4 laps × 1,67 km √M | 1M multiply by lap distance | MP |
5.2.3 | Difference in Time = 19 min 30 sec − 15 min 45 sec √M | 1M subtract time | MP |
5.3.1 | Number of candles | 1MA ÷ by correct values OR 1MA × by correct values | MP |
5.3.2 | Total area = 2 (H × L) + 2 (W × H) √C | 1C converting to m | M |
[30] | |||
TOTAL: 150 | |||
Mathematical Literacy Paper 2 Addendum - Grade 12 September 2021 Preparatory Exams
ADDENDUM
ANNEXURE A
QUESTION 2.1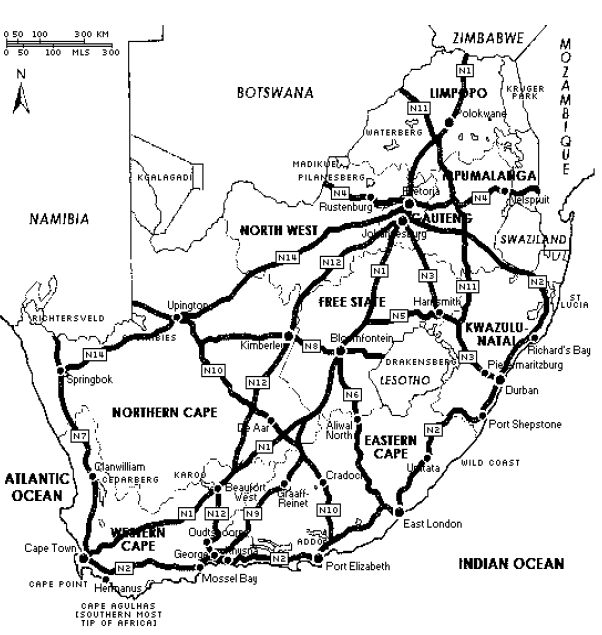
[Source: www.sa-venues.com]
ANNEXURE B
QUESTION 4.1 – LOW-COST HOUSE FLOOR PLAN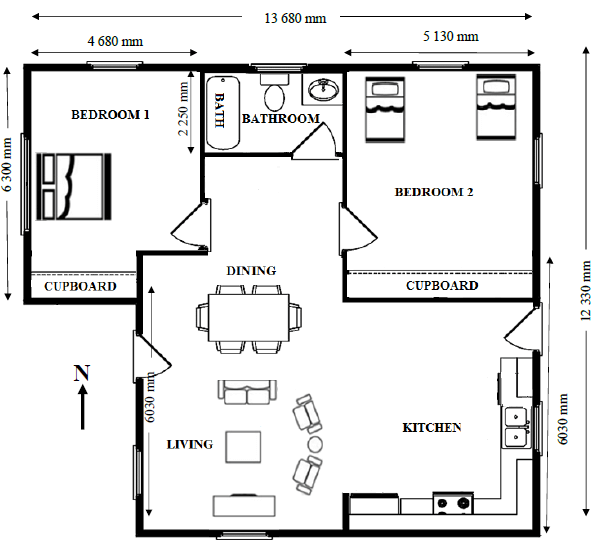
[Adapted from www:pinterest.com]
Mathematical Literacy Paper 2 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions.
- Use the ANNEXURE in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 2.1
- ANNEXURE B for QUESTION 4.1
- Answer ALL the questions.
- Number the questions correctly according to the numbering system used in this question paper.
- Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise.
- Round off ALL the final answers appropriately according to the context used, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Start EACH question on a NEW page.
- Show ALL calculations clearly.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1
South Africans require the following tablets to boost their immune systems during winter. The pictures below show two types of prescriptions to use namely vitamin C and Zinc capsules:
The table below shows the types of essential vitamins adults consume daily to keep their immune system strong.
NOTE: Adults use 2 capsules daily per prescription. |
Study the table above and answer the questions that follow.
1.1.1 Write as a ratio in simplified form the Zinc mg per tablet to Vitamin C mg per tablet. (2)
1.1.2 Calculate how many milligrams of Zinc an adult takes per week. (3)
1.1.3 Mr Smith purchased the Vitamin C tablets on the 28th February 2021. He decided to use the medicine as prescribed daily from the next day. Determine by which date he will need a refill of Vitamin C tablets. (3)
1.1.4 Determine the total number grams of Zinc contained by an entire bottle of Zinc. (3)
1.2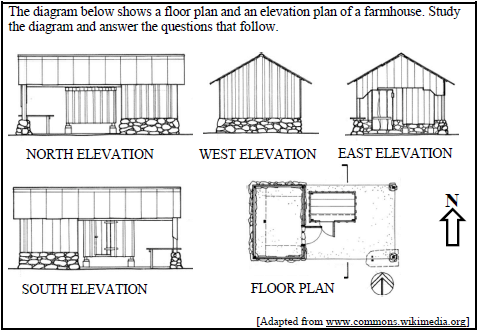
1.2.1 Explain the meaning of ‘North Elevation’ on the diagram. (2)
1.2.2 Refer to the diagram above. Define the following terms respectively:
- A floor plan (2)
- An elevation plan (2)
1.2.3 Use the scale of 1 : 100 to determine the actual length in centimetres on the plan if the measured length is 5 cm. (2)
1.3
Mr Dudley, a farmer, travels from his farm to the city once a week. The distance from the city to his farm is 90 km. He plans to buy 4 boxes of tiles to replace some broken tiles in his kitchen. |
1.3.1 Convert 90 km to mm. (2)
1.3.2 Calculate the number of tiles packed in ONE box, if the area of 1 tile is 0,36 m2 and the tiles are sold at 1,44 m2 per box. (2)
1.3.3 Mr Dudley takes 1,125 hours to travel to town. Convert this time to hours, minutes, and seconds. (3)
[26]
QUESTION 2
2.1
The Fisher family, consisting of the wife, husband and son, plans to spend the festive season with friends in Gqeberha (Port Elizabeth) and then proceed to Johannesburg.
A map of South Africa and all the national routes are shown on ANNEXURE A. |
Study the map on ANNEXURE A to answer the questions that follow.
2.1.1 Write down the names of TWO towns they will be passing through on their trip to Port Elizabeth. (2)
2.1.2 Give TWO general directions used when travelling from Cape Town to Johannesburg via Port Elizabeth. (4)
2.1.3 State TWO advantages of using national roads. (4)
2.1.4 Use the bar scale on ANNEXURE A to calculate the actual distance between Cape Town and Port Elizabeth. Show ALL calculations. Give your answer to the nearest km. (4)
2.1.5 The Fisher family is travelling at an average speed of 100 km/h. Prove by means of calculations whether they will be able to reach Port Elizabeth at the planned time.
The following formula may be used: Distance = Average Speed x Time (7)
2.2
The price of petrol is 1 642 cents per litre. Mr Fisher drives a Jeep Wrangler with a fuel capacity of 75 litres. The Jeep has a fuel consumption of 7,6 litres per 100 km. |
2.2.1 Calculate the amount of petrol that will be used for a return trip to Port Elizabeth. (4)
2.2.2 Determine the petrol cost for the return trip in rands (R) from Cape Town to Port Elizabeth. (3)
[28]
QUESTION 3
3.1
Mr Johnathan and his wife decided to arrange a birthday party for their only daughter. They purchased a two layered round chocolate cake at a bakery. The diameter of the bottom layer is 250 mm and the diameter of the top layer is 18 cm.
|
Refer to the diagram above and answer the questions that follow.
3.1.1 Determine A, the area indicated on the top layer of the chocolate cake in square millimetres (mm2). Give your answer to the nearest whole millimetres. (5)
3.1.2 A ribbon will be wrapped around the circumference of the bottom layer cake and must overlap by 50 mm. Calculate the length of the ribbon in mm.
You may use the formula:
Circumference = 2 × π × radius where π = 3,142 (4)
3.1.3 The volume of the rectangular cardboard box is 42 000 cm3. Determine the height of the box in cm. (4)
3.1.4 Mr Johnathan’s cousin in England claims that the diameter of the bottom layer cake is more than 10 inches. Verify with the necessary calculation if his claim is valid or not. (3)
3.1.5 According to the baker at the bakery, the height of the bottom layer of the cake is 64% of the radius. Calculate the height of the bottom layer in mm. (3)
3.1.6 The recipe for the chocolate cake needs flour to sugar in a ratio of 7 : 3. Determine the number of cups of flour needed if 6 cups of sugar are used. (3)
3.1.7 Mr Johnathan’s wife plans to bake a similar one-layer chocolate cake for a tea party. She received the recipe from a friend in the United Kingdom. According to the recipe, the baking temperature should be at 365 °F (Fahrenheit). Determine the temperature in degrees Celsius. Give your answer to the nearest 10 degrees Celsius.
You may use the following formula: °C = (°F – 32°) ÷ 1,8 (3)
3.2
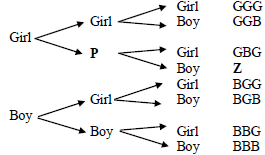
Mr Johnathan and his wife plan to have two more children. Study the diagram below:
|
3.2.1 Identify the type of diagram shown above. (2)
3.2.2 Write down the appropriate items for P and Z. (2)
3.2.3 Determine the probability for Mr Johnathan and his wife of:
- Getting at least two girls (as a fraction in simplified form) (3)
- Getting a boy, then a girl, then a boy (as a percentage) (2)
[34]
QUESTION 4
4.1
ANNEXURE B shows the drawing of the floor plan of a low-cost house. Study the floor plan and answer the questions that follow. |
4.1.1 Identify the feature you will find upon entering the bathroom. (2)
4.1.2 Write down the number of windows facing southwards. (2)
4.1.3 Determine the length of the interior bathroom wall (excluding the door) that is not given, if the door takes up a space of 860 mm. (6)
4.2
The kitchen and bathroom should be tiled. The floor tile dimension is 500 mm x 500 mm. When buying tiles, you need to buy 5% more to cater for breakages. A tiling company charges R8 186,09 for labour and can get the tiles at R249,90 per box.
|
Refer to the information above to answer the questions that follow.
4.2.1 Calculate the total area that must be tiled in m2. (9)
4.2.2 The building manager made the statement that 150 tiles are needed to complete tiling for the kitchen and bathroom. Verify with a calculation whether his statement is valid or not. (7)
4.2.3 The tiling company charged R24 795,00 for the cost of tiles and labour. The manager of the low-cost housing claims that the tiling company's quotation is exceptionally high. Verify, with the necessary calculations, whether the manager's claim is valid or not.
NOTE: Each box has 4 tiles. (6)
[32]
QUESTION 5
5.1
A young rugby player is concerned about his weight. He weighs himself before joining a gymnasium and calculates that his BMI (Body Mass Index) is 25,1 kg/m2. He has a height of 175 cm. The table below shows the weight status versus the BMI ranges. TABLE 2: WEIGHT STATUS ACCORDING TO BMI
|
Refer to the table provided above and answer the questions that follow.
5.1.1 Use the information above to calculate his current weight (mass). You may use the formula below:
BMI = Mass in kg (4)
(Height × Height) in metres
5.1.2 Write down the young player’s current weight status. (2)
5.1.3 Provide advice to him on how to improve his BMI status. (2)
5.2
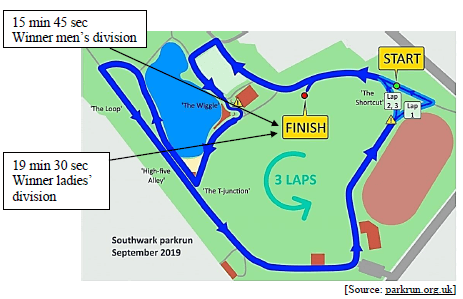
The map of Southwark Park Run course is shown below. Runners are required to complete 3 laps to finish the race. A parkrun is a 5 000 m distance run. On a certain Saturday, Douglas Cameron was the winner of the men's division with a time of 15 min 45 seconds. Sarah Caroll, a fellow park run tourist at Southwark Park was the winner of the lady’s division with a time of 19 min 30 seconds.
|
Study the information and map above and answer the questions that follow.
5.2.1 If the total distance is 5 000 m, determine the length of 1 lap in kilometres. (3)
5.2.2 Douglas Cameron was very unfit when he started off participating in park runs and did not complete all his laps initially. He claims that he completed a total distance of 23,33 km for his first 5 park runs. Prove by calculation whether his statement is valid. Refer to the table below.
TABLE 3: SUMMARY OF DOUGLAS CAMERON’S PARK RUN RACES (5)
Date of park run | Distance in metres | Number of laps completed |
07/09/2019 | … | 2 |
14/09/2019 | … | 2 |
21/09/2019 | 5 000 | 3 |
28/09/2019 | 5 000 | 3 |
05/10/2019 | 5 000 | 3 |
5.2.3 Sarah Caroll made the statement that the difference in minutes between her average time per lap of 6,5 minutes (6 min 30 sec) and Douglas’ average time per lap is less than 2 minutes. Verify with the necessary calculations whether her statement is valid. (5)
5.3
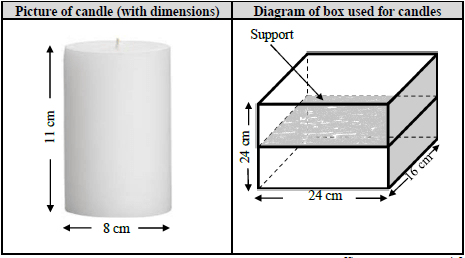
James decided to distribute candles to local churches. He would like to pack cylindrical candles into a rectangular container for distribution. Each candle is 11 cm high and measures 8 cm in diameter.
|
Study the picture and diagram above and answer the questions that follow.
5.3.1 James realises that he can pack the candles on top of each other if he places a support that is 10 mm thick, between the layers. The container that he uses is 24 cm high, 16 cm wide and 24 cm long. Calculate how many candles he can pack into this container. (5)
5.3.2 James prints a label that covers the sides of the container. Calculate the area of the label in m2. You may use the following formula:
Area of all sides = 2 (length × height) + 2 (width × height) (4)
[30]
TOTAL: 150
Mathematical Literacy Paper 1 Memorandum - Grade 12 September 2021 Preparatory Exams
Symbol | Explanation |
M | Method |
MA | Method with accuracy |
CA | Consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
RT/RG/RM | Reading from a table/Reading from a graph/Reading from a map |
F | Choosing the correct formula |
SF | Substitution in a formula |
J | Justification |
P | Penalty, e.g., for no units, incorrect rounding off etc. |
R | Rounding Off/Reason |
AO | Answer only |
NPR | No penalty for rounding |
MEMORANDUM
QUESTION 1 [30 MARKS] | |||||
Ques | Solution | Explanation AO: FULL MARKS | T&L | ||
1.1.1 | Deposit as % of lay-bye price = 1200 × 100% M | 1M percentage calculation | F L1 | ||
1.1.2 | Months = 3 600 A | 1A identifying use of R3 600 | F L1 | ||
1.1.3 | Balance = R3 600 – (R400 × 7) M OR Balance of months = 2 | 1M for subtracting 7 instalments from R3 600 | F L1 | ||
1.2.1 | Cost price = R60 + R45 + R5 M | 1M adding correct values | F L1 | ||
1.2.2 | Profit = R176 – R110 M | 1M subtracting cost price from selling price | F L1 | ||
1.2.3 | RT | 2RT for the R176n (2) | F L1 | ||
1.2.4 | Cash discount = 15 × 176 MA | 1MA discounted percentage calculation | F L1 | ||
Ques | Solution | Explanation | T&L |
| 1.3.1 | Cost of a dozen = 110 × 12 MA OR Dozens = 60 | 1MA divide by 60 and multiply by 121A dozen cost 1M divide by 12 to get number of dozens. 1MA cost of a dozen answer (2) |
|
| 1.3.2 | Profit = R125 – R110 | 1M profit calculation 1M average calculation | F |
1.4.1 | Total population in 2001(44 819 778): A | 2A correct value in words (2) | D L1 |
1.4.2 | Increase in total population = 51 770 560 – 40 583 573M | 1M subtraction correct values | D L1 |
1.4.3 | Difference in population between KZN and NC in 1996 | 1RT correct values | D L1 |
1.4.4 | Northern Cape RT | 2RT correct province (2) | D L1 |
[30] |
QUESTION 2 [31 MARKS] FINANCE | |||
Ques | Solution | Explanation/Marks AO: FULL MARKS | T/L |
2.1.1 | Amoti: Dan = 3 : 5 [8 shares] | 1MA 3/8 of the investment. | F |
2.1.2 | Dan’s share of profit = 3/8 × 2 880 M | 1M fraction of the profit | F L1 |
| 2.1.3 | Amoti's interest: R2880 – R1080 OR Amoti’s investment = 16 000 × 5 | 1MA Amoti’s interest 1MA Mary’s amount at end of 1st year.
OR 1A investment amount | F L4 |
Ques | Solution | Explanation | T&L |
2.2.1 | R147,74 RT | 2RT correct amount (2) | F |
2.2.2 | Block 1: Cost 550 × 124,49 = 68 469,5 cents M | 1M cost of 550 kWh | F |
2.2.3 | VAT amount included = 15 × ?1 465,68 M OR VAT exclusive amount = R1 465,68 ÷ 1,15 M VAT amount = R1 465,68 – R1 274,50 | CA from 2.2.2 | F |
2.3.1 | 12 Months RT | 2RT correct months (2) | F |
| 2.3.2 | Total income = R101 677 + R91 785 + R453 000 = R646 462 M Difference = Income ─ Expenses | 1M finding total income | F |
2.3.3 | Monthly charges = 1080RT M | 1RT yearly charges | F |
[31] |
QUESTION 3 [29 MARKS] | ||||||||||
Ques | Solution | Explanation | T&L | |||||||
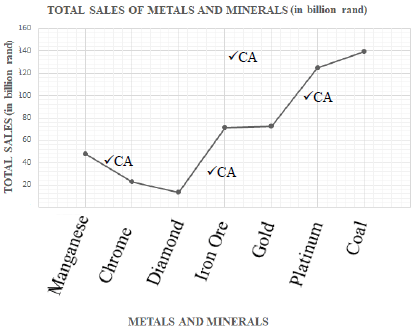
3.1 | Gold RT | 2RT correct mineral (2) | D L1 | |||||||
3.2 | Median (Total sales): OR = 71 400 000 000 | 1M arranging in order | D L2 | |||||||
3.3 | Q1 = 22,8 M | 1M for Q1 | D | |||||||
| 3.4 | Mean = 10 846 + 19 693 + 15 728 + 19 092 + 95 130 + 164 513 + 92 230 M = 417 232 ¸ 7 M | 1M adding all values | D | |||||||
3.5 | Modal value = 2,1 billion M | 1M value of modal value | D L2 | |||||||
Ques | Solution | Explanation | T&L | |
3.6 | 802 000 000 + 362 000 000 + 2 100 000 000 + 288 000 000 + 1 120 000 000 + 2 100 000 000 OR 0,802 + 0,362 + 2,1 + 0,288 + 1,12 + 2,1 | 1MA finding total royalties 1M percentage calculation | (3) | D |
3.7 | P = 3 ×100% A M 7 = 42,86% CA | 1A numerator | (3) | P L2 |
3.8 |
First 2 minerals/metals correctly plotted; 1CA | (4) | D L2 | |
| 3.9 | RT | 1RT correct values
| (3) | D L2 |
| [29] | ||||
QUESTION 4:[32 MARKS] FINANCE | |||||
Ques. | Solution | Explanation/Marks | T&L | ||
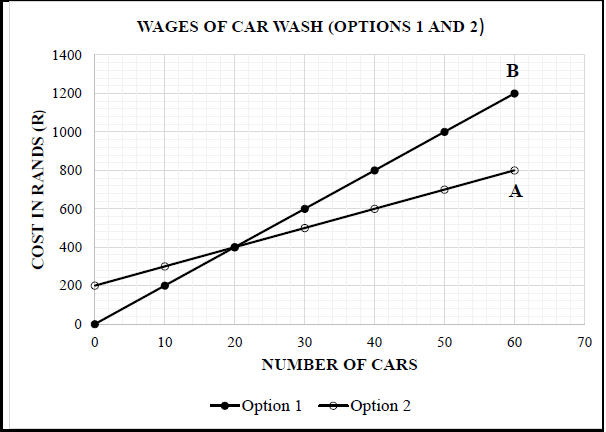
4.1.1 | Option 1: B RT OR A: Option 2 RT | 1RT correct option | F L2 | ||
4.1.2 | Breakeven point is where the income under option 1 is equal to the income under option 2. A | 2A explanation (2) | F | ||
4.1.3 | Use of calculations Option 2. Difference = R320 – R240 = R80 MA OR From Graph Option 2 | 1SF substitution in formula 1SF substitution in formula 1MA finding the difference | F | ||
Ques, | Solution | Explanation/Marks | T&L | |
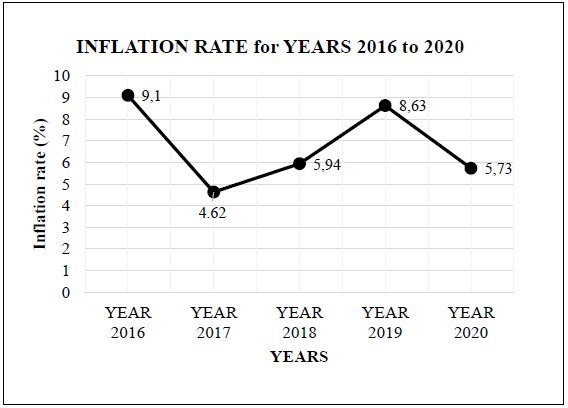
4.2.1 | Average Inflation rate because it involves an increase of different goods over a period of time. O | 2O Reasoning (2) | F L1 | |
4.2.2 | RT | 1RT rate decreased from 2016 to 2017 1O prices of goods increase at lower rate | F L4 | |
4.2.3 | New price = old price × (100% + Inflation rate%) | 1SF substitution 1M changing subject of the formula
| F L3 | |
Ques. | Solution | Explanation/Marks | T&L |
4.3.1 | Nigeria RT | 2RT correct answer (2) | D |
4.3.2 | RT RT | 1RT correct month and year | D |
4.3.3 |
| 2J increasing from April 2020 to May 2021. (2) | D D |
[32] |
QUESTION 5: [28 MARKS] FINANCE; DATA HANDLING AND PROBABILITY | |||
Ques | Solution | Explanation | T&L |
| 5.1.1 | Basic annual salary = R27 678 × 12M Taxable Income = R332 136 – (7,5% of 332 136) M Annual tax before rebates. Annual tax after rebates = R63 406,50 ─ 14 958 Monthly tax after rebates = 48 448,50 MA | 1M multiply by 12 1CA annual salary | F |
5.1.2 | Monthly pension = 24 910,20 ÷ 12 | 1M monthly pension | F L2 |
Ques. | Solution | Explanation | T&L | ||
5.2.1 | Mary: age 16 years and BMI = 29 from graph gives 95% percentile | 1RT reading from the growth chart | D | ||
5.2.2 | From the Growth chart: | 2RT using the 19 and 85% to get BMI = 26 | D | ||
5.3.1 | Total = 1 063 038 + 130 092 + 129 056 + 784 314 OR Total = 757 105 + 1 349 395 | 1M adding all values 1M adding all values | D | ||
5.3.2 | Probablity is the chances or likelihood of an event occurring. A | 2A explanation (2) | P | ||
5.3.3 | P(Black African with a degree) = 613 820 A | 1A numerator | P | ||
[28] | |||||
TOTAL: 150 | |||||
Mathematical Literacy Paper 1 Addendum - Grade 12 September 2021 Preparatory Exams
ADDENDUM
ANNEXURE A: QUESTION 1.4
DEMOGRAPHICS:
TABLE 1: POPULATION COUNTED IN CENSUS 1996, 2001 AND 2011 BY PROVINCE
Year | WC | EC | NC | FS | KZN | NW | GP | MP | LP | SA |
1996 | 3 956 875 | 6 147 244 | 1 011 864 | 2 633 504 | 8 572 302 | 2 727 223 | 7 834 125 | 3 123 869 | 4 576 566 | 40 583 573 |
2001 | 4 524 335 | 6 278 651 | 991 919 | 2 706 775 | 8 584 129 | 2 984 098 | 9 388 854 | 3 365 554 | 4 995 462 | 44 819 778 |
2011 | 5 822 734 | 6 562 053 | 1 145 861 | 2 745 590 | 10 267 300 | 3 509 953 | 12 272 263 | 4 039 939 | 5 404 868 | 51 770 560 |
[Source: SASTAT 2021]
ANNEXURE B: QUESTION 2.3
GMT Missions Shelter: Financial Report | |||
For period 1 March 2020 – 28 February 2021 | |||
INCOME | EXPENSES | ||
Item | Amount (in Rand) | Item | Amount (in Rand) |
Member donations: | Salary for house matron | 114 859,00 | |
-> Local | 101 677,00 | Salaries for casual labour | 123 567,00 |
-> Foreign | 91 785,00 | Rates | 14 600,00 |
Subsidy from the local municipality | 453 000,00 | Electricity and water | 23 982,00 |
Telephone | 3 679,00 | ||
Stationery/postage | 1 650,00 | ||
Bank charges | 1 080,00 | ||
Food | 146 912,00 | ||
School uniforms | 17 244,00 | ||
Clothing | 43 432,00 | ||
Maintenance and gardening | 12 456,00 | ||
Transport costs | 23 678,00 | ||
TOTAL INCOME | 646 462,00 | TOTAL EXPENSES | … |
ANNEXURE C: QUESTION 5.2
GROWTH CHART AND WEIGHT STATUS TABLE
Girls: 2–20 years
BMI – for – age chart: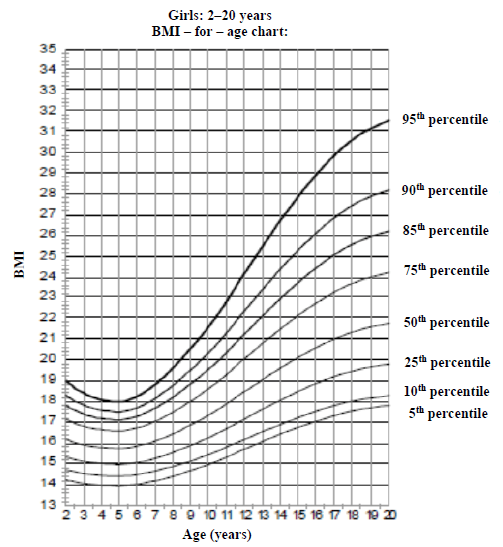
ANNEXURE D: QUESTION 5.2
TABLE 6: WEIGHT STATUS
BMI FOR AGE PERCENTAGE RANGE | WEIGHT STATUS |
< 5th percentile | Underweight |
5th percentile to 85th percentile | Healthy |
85th percentile to 95th percentile | Risk of overweight |
≥ 95th percentile | Overweight |
Mathematical Literacy Paper 1 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions. Answer ALL the questions.
- 2.1 Use ANNEXURE A for QUESTION 1.4 ANNEXURE B for QUESTION 2.3 ANNEXURE C for QUESTION 5.2 ANNEXURE D for QUESTION 5.2
2.2 Write your NAME and GRADE in the spaces provided on the ANSWER SHEET FOR QUESTION 3.8 (GRAPH).
Hand in the ANSWER SHEET with your ANSWER BOOK. - Number the answers correctly according to the numbering system used in this question paper.
- Diagrams are not necessarily drawn to scale, unless stated otherwise.
- Round off ALL final answers according to the context used, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Start EACH question on a NEW page.
- Show ALL calculations clearly.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1
James bought a double bed on lay-by for R4 800. He paid a deposit of R1 200 and opted to pay instalments of R400 each month to complete the balance of R3 600. |
[Adapted from russels.co.za] |
1.1.1 Express the deposit as a percentage of the lay-by purchase price. (2)
1.1.2 Determine the number of months to complete paying for the balance. (3)
1.1.3 Calculate the balance amount after James paid the deposit and seven instalments. (2)
1.2
Morgan started an online clothing store. The t-shirt below was designed in association with the The Saartjie Baartman Centre for Women and Children, to make people aware of women and children abuse. Below are the cost structures for this t-shirt.
|
[Source: www.clothingcloset.com] |
1.2.1 Write down the cost price that Morgan must pay to get the t-shirt ready for sales. (2)
1.2.2 Calculate the profit she will make on one (1) t-shirt. (2)
1.2.3 Complete the income formula for Morgan below: Income (Rands) = … where n stands for the number of t-shirts sold. (2)
1.2.4 As a special during Woman’s Month, she runs a promotion on Facebook with a 15% discount. Calculate the cash discount. (3)
1.3
| Mary bought a tray of 60 eggs at a cost of R110. She sold half of the eggs at a price of R65 and the remaining eggs at a price of R60. |
1.3.1 Calculate the cost price of a dozen eggs. (2)
1.3.2 Calculate the average profit per egg made from the sale of the 60 eggs. (3)
1.4
| The population of South Africa in 1996; 2001 and 2011 is indicated in the TABLE 1 in ANNEXURE A. |
Use ANNEXURE A to answer the questions that follow.
1.4.1 Write down the total population of South Africa in 2001 in words. (2)
1.4.2 Determine the increase in the total population of South Africa from 1996 to 2011. (2)
1.4.3 Write down the difference in population between the KZN and NC provinces in 1996. (3)
1.4.4 Write down the province whose total population decreased in the 2001 census compared to the census. (2)
[30]
QUESTION 2
2.1
On the 1st January 2019, Amoti and Dan invested in a school canteen business. They invested a total of R16 000 in the ratio of 5 : 3 respectively. For the same period Mary chose to invest R10 000 in ADC Bank that offered her an interest rate of 8,5% per annum compounded annually. |
Use the above information to answer the questions that follow.
2.1.1 Calculate the amount Dan invested in the school canteen business. (2)
2.1.2 Determine Dan’s share of the profit on his investment after two years. (2)
2.1.3 Calculate the total interest Mary earned in 2 years, and compare it with Amoti’s share of their profit, to verify who had the better investment. (6)
2.2
Mr Amoti studied his electricity bill and saw that he used 690 kWh of energy for the previous month. TABLE 2: ELECTRICITY TARIFFS FOR FLATS / HOUSES
[Adapted from electricity-tariffs 2018–2019-Johannesburg] |
Use the information in TABLE 2 above to answer the questions that follow.
2.2.1 Write down the monthly service charge (in Rands) to be paid for a flat or house. (2)
2.2.2 Calculate the electricity bill (in Rands) for Mr Amoti for the previous month. (5)
2.2.3 Calculate the VAT amount included in the electricity bill paid for a domestic use of 690 kWh of energy. (3)
2.3
| The GMT Missions Shelter is a non-profit organisation that provides shelter, food, clothing and schooling to abandoned and destitute children. The treasurer of the organisation presented a financial report to all its stakeholders for the 2020/2021 financial year as shown in ANNEXURE B. |
Use the above information and ANNEXURE B to answer the questions that follow.
2.3.1 Determine the time period of the financial report, in months. (2)
2.3.2 Verify, showing all calculations, whether the GMT Missions Shelter organisation has shown a surplus or a deficit. (6)
2.3.3 Calculate the average monthly amount that was paid for bank charges. (3)
[31]
QUESTION 3
Mining plays a significant role in the economy of our nation. The information below indicates how the mining industry performed in 2019.
|
Use the above information in TABLE 3 to answer the questions that follow.
3.1 Identify the type of ‘metals and minerals’ that paid the lowest amount of royalties. (2)
3.2 Determine the median value for the total sales. (3)
3.3 Use calculations to determine if the interquartile range for the total sales of the metals and minerals is less than 101 billion rand. (5)
3.4 Determine the mean number of direct employees in the mining industry. Give your final answer to the nearest thousand. (4)
3.5 Write down the modal value for ‘royalties paid’. Give your answer in number format / figures without words. (2)
3.6 Express the gold amount paid on royalties as a percentage of the total amount paid on royalties. (3)
3.7 Calculate the probability (expressed as a percentage) of randomly selecting a type of ‘metals and minerals’ that had less than 19 500 direct employees in 2019. (3)
3.8 On ANSWER SHEET 1 draw a broken line graph showing the total sales for all metals and mineral industries mentioned above. (4)
3.9 Determine the difference in tons between the ‘Production’ of iron ore and gold for the year 2019. (3)
[29]
QUESTION 4
4.1
Sipho is working at Shining Cars Car Wash and has the following wage options: He receives R20 for every car that he washes, OR R200 per day plus R10 per car that he washes. The equations representing the options are:
|
Use the above information and the graph to answer the questions that follow.
4.1.1 Write down the graph which indicates option 1 and option 2. Use letters A and B. (2)
4.1.2 Explain the meaning of break-even point in this context. (2)
4.1.3 Sipho opted for wage option 2. He washed 12 cars on the first day. Verify, showing all calculations or by use of the graph that if he had chosen option 1, he would have earned R80 less for the day. (6)
4.2
The average inflation rate for South Africa for the period 2016 to 2020 is indicated in the graph below. SOUTH AFRICA’S AVERAGE RATE OF INFLATION FROM 2016 TO 2020
[Source: Statista.com /370515/Inflation rate in South Africa] |
Use the above information on the graph to answer the questions that follow.
4.2.1 Explain why it is referred to as the average inflation rate. (2)
4.2.2 Briefly explain the changes in the rate of inflation and the impact it had on the prices of goods from 2016 to 2019. (4)
4.2.3 The price of a dining table was R5 356 in 2018. Use the rates of inflation shown above to calculate the difference in its price in 2017 and 2019.
You may use the formula:
New price = Old price × (100% + Inflation rate %) (7)
4.3 The following graph shows the Consumer Price Inflation (CPI) of South Africa, Nigeria, and Botswana for the period January 2020 until March 2021.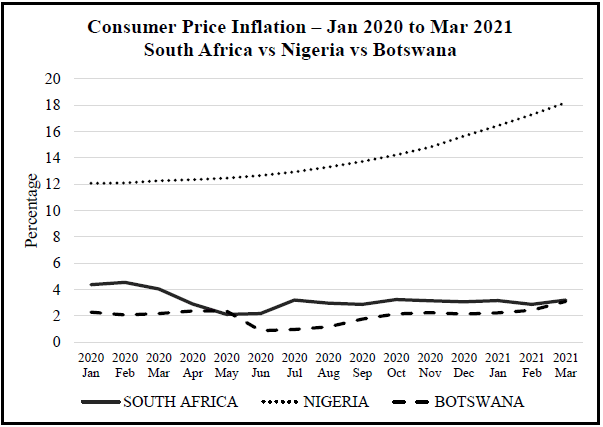
Study the graph above and answer the questions that follow.
4.3.1 Identify the country with the highest Consumer Price Inflation (CPI) over the period shown in the graph. (2)
4.3.2 Write down the month and year when the CPI of South Africa and Botswana was the closest to each other. (2)
4.3.3 Describe the trend of:
- Nigeria (from April 2020 until March 2021) (2)
- South Africa (from March 2020 until July 2020) (3)
[32]
QUESTION 5
5.1
TABLE 5 below shows the rates of tax that individuals in South Africa are liable to pay for the 2020/2021 tax year. |
TABLE 5: TAX RATES FOR INDIVIDUALS – 1 MARCH 2020 TO 28 FEBRUARY 2021
Rates applicable to individuals 2021 tax year (1 March 2020 – 28 February 2021) | |
Taxable Income (R) | Rates of Tax (R) |
1 – 205 900 | 18% of taxable income |
205 901 – 321 600 | 37 062 + 26% of taxable income above 205 900 |
321 601 – 445 100 | 67 144 + 31% of taxable income above 321 600 |
445 101 – 584 200 | 105 429 + 36% of taxable income above 445 100 |
584 201 – 744 800 | 155 505 + 39% of taxable income above 584 200 |
744 801 – 1 577 300 | 218 139 + 41% of taxable income above 744 800 |
1 577 301 and above | 559 464 + 45% of taxable income above 1 577 300 |
Age Category Rebates Tax threshold * Below age 65 R14 958 R83 100 * Age 65 to below 75 R8 199 R128 650 * Age 75 and older R2 736 R143 850 | |
Use the information in TABLE 5 above to answer the questions that follow.
5.1.1 Mr Buti, a 55-year-old salesman earned a gross income of R27 678 per month during the 2020/2021 tax year. A monthly deduction of 7,5% was made from his salary and paid into his pension fund.
Show, by means of calculations, that Mr Buti’s monthly tax was R4 037,38. You may use the formula:
Taxable Income = Annual Gross Income – Annual Pension (8)
5.1.2 Mr Buti is a member of a union and has a savings policy with an insurance company. In addition to his monthly tax of R4 037,38, he pays the following:
- Union Membership fee: R106 per month
- Savings policy premium: R585,64 per month
Hence, calculate Mr Buti’s monthly net income. (4)
5.2
A Grade 12 Mathematical Literacy class was taught how to use BMI (Body Mass Index), growth charts and weight status chart based on BMI in a data handling lesson.
|
Use the information above, Growth chart in ANNEXURE C and weight status TABLE 6 in ANNEXURE D to answer the questions that follow.
5.2.1 Mary and Jolly interpreted their weight status using their data, growth charts and TABLE 6 for weight status and had the following opinions:
- Mary: Both are at risk of overweight
- Jolly: Both are overweight
Verify, by giving explanations, whose interpretation is correct. (5)
5.2.2 Use the growth chart to estimate by how many BMI-points Mary will need to reduce her BMI to get to the 85th percentile, if she plans to achieve her target by her 19th birthday. (4)
5.3 Study the table below showing the number of adult individuals aged 20 and older who have attained a tertiary qualification by type of qualification and population group in 2016.
Type of qualification | Black African | Coloured | Indian/ Asian | White | Total |
Certificates/Diplomas | 449 218 | 54 756 | 37 931 | 215 200 | 757 105 |
Degrees | 613 820 | 75 336 | 91 125 | 569 114 | 1 349 395 |
TOTAL | 1 063 038 | 130 092 | 129 056 | 784 314 | … |
[Adapted from www.statssa.gov.za]
5.3.1 Calculate the total number of adult individuals who attained tertiary qualifications. (2)
5.3.2 Explain the meaning of the term ‘probability’. (2)
5.3.3 Determine the probability (as a decimal) of randomly selecting a Black African with a degree from all the individuals with a degree. (3)
[28]
TOTAL: 150
ANSWER SHEET 1 (QUESTION 3.8)

Mathematics Paper 2 Memorandum - Grade 12 September 2021 Preparatory Exams
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST
- If a candidate has crossed out an attempt of a question and not redone the question, mark the crossed out
- Consistent accuracy applies in ALL aspects of the marking Stop marking at the second calculation error.
- Assuming answers/values in order to solve a problem is NOT
GEOMETRY | |
S | A mark for a correct statement |
R | A mark for the correct reason |
S/R | Award a mark if statement AND reason are both correct |
MEMORANDUM
QUESTION 1
Temperature (in °C) | 14 | 24 | 26 | 18 | 20 | 28 | 22 | 17 | 12 | 19 |
Number of hot drinks sold | 410 | 258 | 192 | 324 | 328 | 156 | 280 | 384 | 230 | 280 |
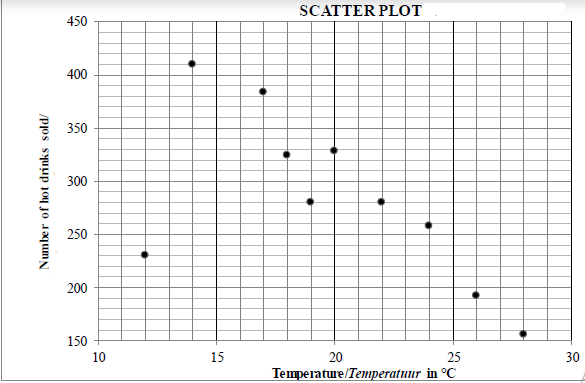
1.1 | As the temperature increases the number of hot drinks sold decreases. | answer | (1) |
1.2 | a = 489,47 |
| (3) |
1.3 | y = 489,47 -10,37x | substitution 314 (accept 313) answer as N0 (3) |
1.4 | The outlier is the point (12; 230). | (12; 230) (1) |
|
| [8] |
QUESTION 2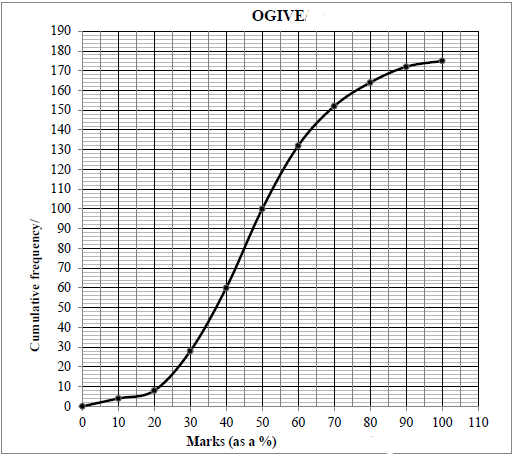
| 2.1.1 | 175 | answer (1) |
| 2.1.2 | 40 ≤ x < 50 OR 40 < x ≤ 50 | answer (1) |
| 2.1.3 | 175 - 158 = 17 | 158 (accept 156 to 160) answer (accept 15 to 19) (2) |
| 2.2.1 | x = 74,87 | answer (2) |
| 2.2.2 | σ = 16,12 | answer (1) |
| 2.2.3 | x + σ = 74,87 + 16,12 = 90,99 3 learners | 90,99 answer (2) |
| 2.3 | x - σ = 82,7 OR x = 82,7 + 94,1 | x = 88,4 answer (3)
x = 88,4 answer (3) |
| [12] |
QUESTION 3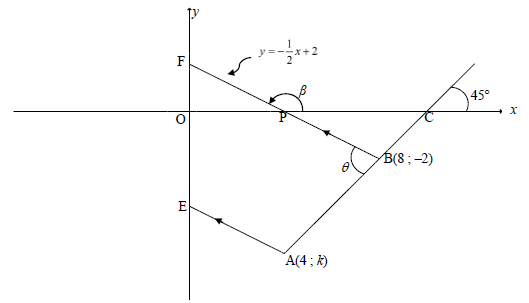
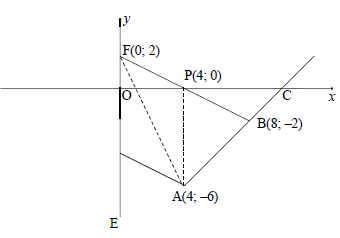
| 3.1 | mAB = tan45º = 1 | mAB = tan45º = 1 (1) |
| 3.2 | y = x +c or tan θ = mAB | equation of AB
Substitute A & B into gradient formula |
| 3.3 | 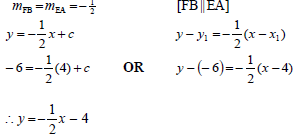 | mEA = -½ substitution of (4 ; -6) equation (3) |
| 3.4.1 | tan β = -½ β = 153,43º θ = 26,565º + 45º [ext < of Δ] =71,57º | tan β = -½ value of β value of θ (3) |
| 3.4.2 | F (0;2) B (8; -2) | F (0;2) substitution answer (3) |
| 3.4.3 |
0 = ½x + 2 OR
y = x + c OR
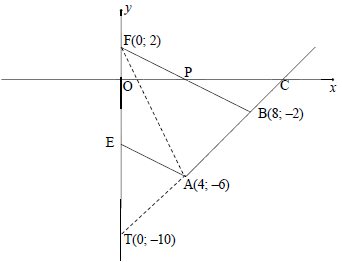
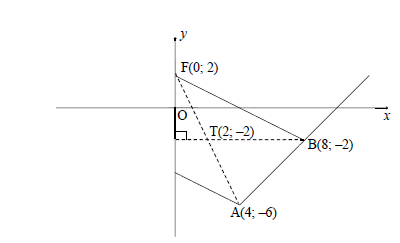
mAF = - 6 - 2 = -2 ∴y = -2x + 2 OR A(4;-6) | P(4;0) area ΔABP area ΔAPF answer (4)
C(0;10) area ΔABT area ΔAFT answer (4)
T(2;-2) area ΔFTB area ΔTBA answer (4)
AB = √32 = 4√2 area formula substitution into area formula anser (4) |
| 3.5 |
RA II Y-axis OR OFP = 153,43º - 90º [ext ∠ of Δ]
PA II y-axis PA II BG | CPB = 26,57º RPB = 90º + CPB RPB answer of PAG (4)
OFP = 63,43º FEA = 180º - 63,43º =116,57º answer of PAG (4)
APC = 90º OR AP = PC PAC = 45º
BAG = θ = 71,57º answer of PAG (4) |
| [20] |
QUESTION 4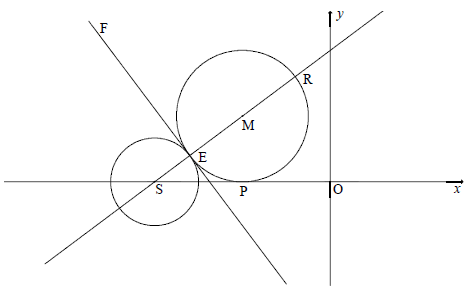
| 4.1.1 | S(-8;0) | x-value y-value (2) |
| 4.1.2 | r = 2 ∴ diameter = 4 units | r = 2 (1) |
| 4.2.1 | ER = 6 units | length of ER answer (2) |
| 4.2.2 | 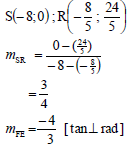 | substitution mSM answer (3) |
| 4.2.3 | EM = MP = 3 units [radii] SM = 5 units | MP = 3 units length of SM length of SP cordinates of M (4) |
| 4.2.4 | 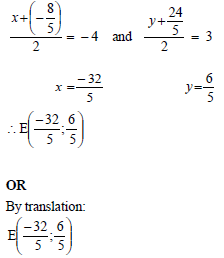 | XE YE (2)
XE YE(2) |
| 4.3 | 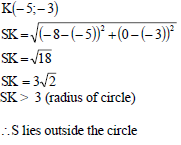 | x-value y-value substitution lenght of SK conclusion (5) |
| [19] |
QUESTION 5
5.1.1 |
tan α = - 2 = 2 | answer (1) |
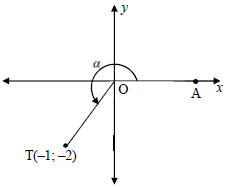
5.1.2 |
| OT = √5 |
5.1.3 | 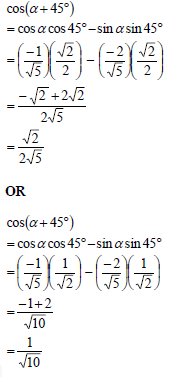 | expansion substitution of sin α special angle ratios answer (4)
expansion substitution of sin α special angle ratios answer (4) |
5.2 | 2sin(-20°).sin160° - cos 40° | - sin 20° sin 20° 1- 2sin2 20° answer (4) |
5.3.1 | 3cos x.sin x + tan x.cos2 (180° - x) | reduction identity simplification single ratio (4) |
5.3.2 | y∈[-2 ; 2] | critical values |
5.4 | cos 3x = 4 cos 2 x - 3 | compound identity 2cos2 x -1 2sin x cos x 1- cos 2 x expansion (5) |
5.5 | 32 tan x - 3tan x+1 = 54 OR ∴ x = 63,43° + k.360°; k ∈ Z or x = 243,43° + k.360°; k ∈ Z | standard from factors both equations tan x = 2 x = 63,43° + k.180°; k ∈ Z (5) OR x = 63,43° + k.360°; k ∈ Z & 243,43° + k.360°; k ∈ Z (5) |
|
| [27] |
QUESTION 6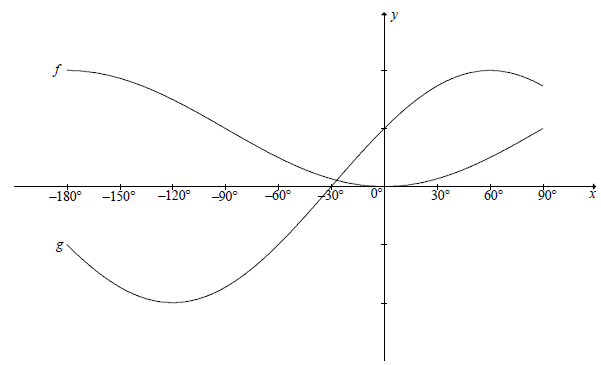
6.1.1 | x ∈[- 30° ;90°] | endpoints notation (2) |
6.1.2 | x = –180° or –60° | –180° –60° (2) |
6.2 | f (x)= - cos(x + 90°)+ 1 | cos x + 90° answer (2) |
|
| [6] |
QUESTION 7 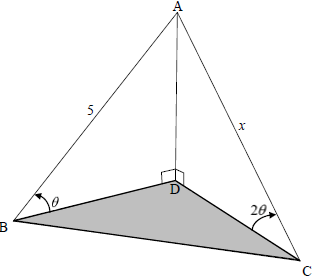
7.1 | sin θ = AD | trig ratio trig ratio 2sinθ cosθ equating AD x as subject (5) |
7.2 |
| use area rule correctly substitution answer (3) |
|
| [8] |
QUESTION 8
8.1 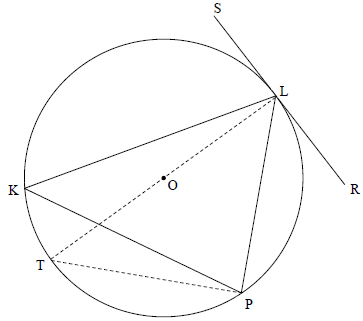
8.1 | Construction: Draw diameter LT and draw TP | Constr S R S /R S R | (6) |
or
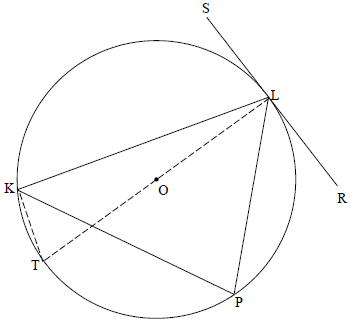
8.1 | Construction: Draw diameter LT and draw KT | construction |
8.2 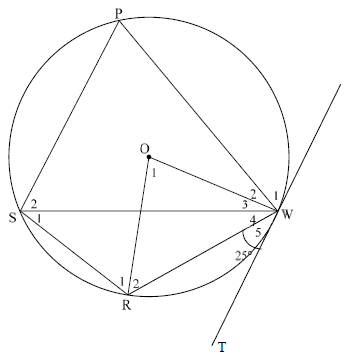
8.2.1(a) | S1 = 25° | [tan chord theorem] | S R | (2) |
8.2.1(b) | O1 = 50° | [∠ at centre = 2x∠ at circumference ] | S R | (2) |
8.2.1(c) | R2 = W3 + W4 = 65° | [∠ s opp = radii ] | S R | (5) |
8.2.2 | W1 = S2 = 60° | [tan chord theorem] | S / R | (3) |
8.3 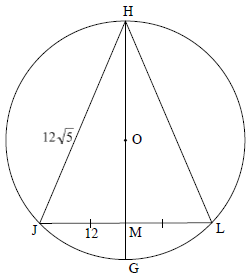
8.3.1 | OG = x + 6 | S |
8.3.2 | OM ⊥ JL [line from centre to midp of chord] OR OM ⊥ JL [line from centre to midp of chord] | S R S R |
|
| [25] |
QUESTION 9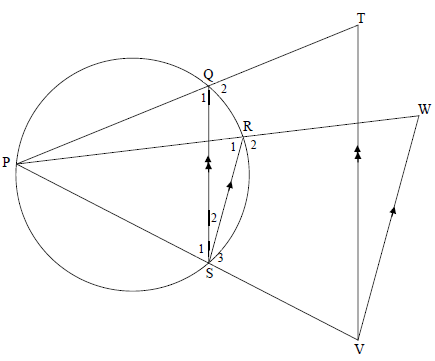
9.1 | TQ = VS [Prop Th , TV || QS ] | S R S/R (3) |
9.2 | Q1 = R1 [∠s in the same segment ] | S R S/R S R (5) |
|
| [8] |
QUESTION 10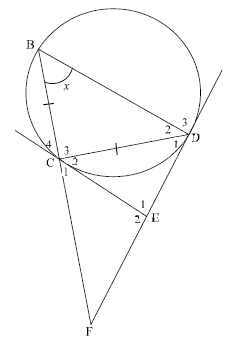
10.1.1 | D1 = x [tan chord theorem ]
OR
D1 = x [tan chord theorem ] | S R S R R
S R SR R | (5)
(5) |
10.1.2 | In Δ ECD and ΔCBD OR In Δ ECD and ΔCBD | S / R S R
S / R S R |
(3)
(3) |
10.2.1 | EC = CD = ED [ Δ ECD ||| ΔCBD] | S CD2 = ED.BD ED = CE (3) |
10.2.2 | C2 = D2 = x [proven ] | S R S R squaring subst CD2 = ED.BD (6) |
|
| [17] |
TOTAL: 150
Mathematics Paper 2 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers correct to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
An annual sports festival is held over a period of 11 days. A tuckshop sells hot drinks at this festival. On each of the first 10 days, the owner of the tuckshop recorded the temperature at 13:00 and the number of cups of hot drinks sold. This information is presented in the table and scatter plot below.
Temperature (in °C) | 14 | 24 | 26 | 18 | 20 | 28 | 22 | 15 | 12 | 19 | |
Number of hot drinks sold | 410 | 258 | 192 | 324 | 328 | 156 | 280 | 384 | 230 | 280 |
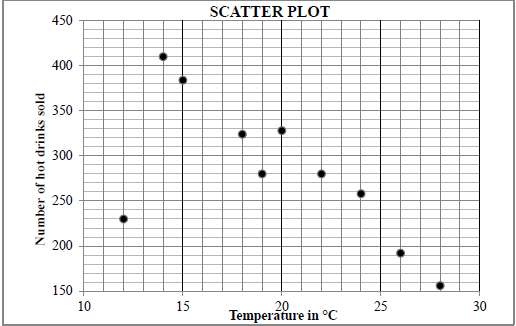
1.1 Describe the trend of the data. (1)
1.2 Determine the equation of the least squares regression line for the data. (3)
1.3 The owner observed that he had used one litre of milk for every 8 cups of hot drinks sold. If the temperature at 13:00 on the 11th day was expected to be 17 °C, predict the number of 1-litre boxes of milk the owner should buy for the 11th day. (3)
1.4 Identify an outlier in the data. (1) [8]
QUESTION 2
2.1 Learners from various schools wrote an aptitude test in order to qualify for a bursary. Their marks (as a percentage) are represented in the ogive (cumulative frequency graph) below.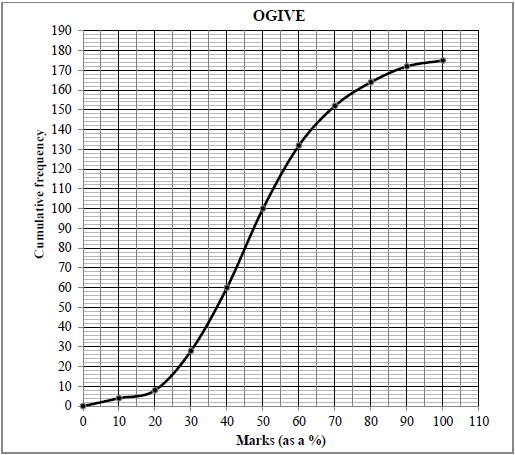
2.1.1 How many learners wrote the test? (1)
2.1.2 Write down the modal class of the data. (1)
2.1.3 The minimum mark to qualify for a bursary is 75%. How many learners qualified for a bursary? (2)
2.2 The table below shows the marks that 15 learners from one particular school obtained in the aptitude test.
Marks (as a %) | 62 | 58 | 78 | 85 | 74 | 48 | 74 | 84 | 100 | 46 | 80 | 92 | 60 | 90 | 92 |
Calculate the:
2.2.1 Mean mark obtained by these learners (2)
2.2.2 Standard deviation of these learners' marks (1)
2.2.3 Number of these learners whose marks lie more than one standard deviation above the mean (2)
2.3 The final Grade 11 marks (as a percentage) obtained by a group of learners was analysed. The one standard deviation interval about the mean was calculated as (82,7 ; 94,1).
Calculate the standard deviation for the final Grade 11 marks. (3) [12]
QUESTION 3
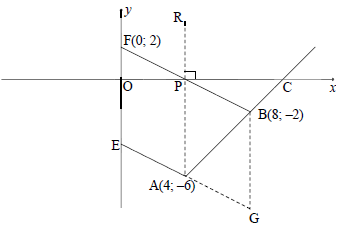
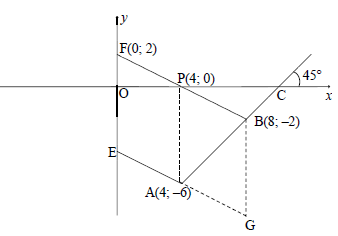
In the diagram below, the line BF is drawn from B(8 ; –2) to cut the x-axis at P and the y-axis at F. The inclination of BF is β and the equation of BF isy = -½x + 2. . From A(4 ; k), another line is drawn parallel to BF and cuts the y-axis at E. The line passing through A and B has an inclination of 45° and cuts the x-axis at C. ABF = θ .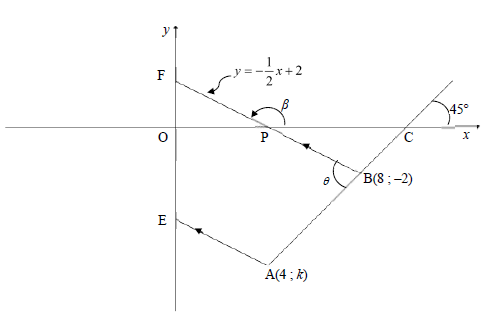
3.1 Calculate the gradient of AB. (1)
3.2 Show that the value of k is –6. (2)
3.3 Determine the equation of EA in the form y = mx + c . (3)
3.4 Calculate the:
3.4.1 Size of θ (3)
3.4.2 Length of BF (3)
3.4.3 Area of ΔABF (4)
3.5 Let G be a point in the fourth quadrant such that APBG is a parallelogram. Calculate the size of PAG. (4)
[20]
QUESTION 4
In the diagram below, S is a point on the x-axis. A circle centred at S and a circle centred at M are drawn. The two circles touch each other externally at E. FE is a common tangent to the circles at E. The circle centred at M, having ER as a diameter, touches the x-axis at P.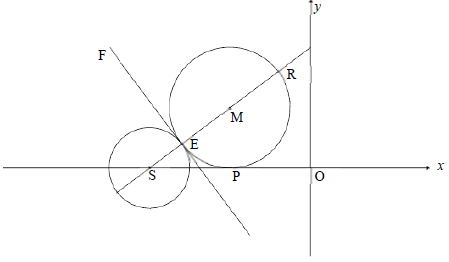
4.1 The equation of the circle centred at S is (x + 8)2 + y2 + 4 .
4.1.1 Write down the coordinates of S. (2)
4.1.2 Show that the diameter of the circle centred at S is 4 units. (1)
4.2 If it is further given that SR = 8 units and ![]() , calculate the:
, calculate the:
4.2.1 Length of EM (2)
4.2.2 Gradient of the tangent FE (3)
4.2.3 Coordinates of M (4)
4.2.4 Coordinates of E (2)
4.3 The circle centred at M(–4 ; 3) is shifted 1 unit to the left and reflected in the x-axis to form a new circle centred at K. Determine whether the point (–8 ; 0) lies inside or outside the circle centred at K. Show ALL calculations. (5)
[19]
QUESTION 5
5.1 Point T(–1; –2) is given in the diagram below. A is a point on the x-axis such that reflex AOT = α.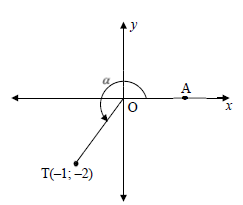
Determine, without using a calculator, the value of each of the following:
5.1.1 tan α (1)
5.1.2 cos α (2)
5.1.3 cos (α + 45º) in simplest form (4)
5.2 Determine, without using a calculator, the value of the following expression:
2 sin(-20º).sin160º - cos 40º (4)
5.3 Consider: 3cos x.sin x + tan x.cos2 (180º - x)
5.3.1 Simplify the expression to a single trigonometric ratio. (4)
5.3.2 Hence, write down the range of:
f (x) = 3cos x.sin x + tan x.cos2 (180º - x) (2)
5.4 Prove the identity: cos 3x = 4 cos2 x - 3 (5)
cos x
5.5 Determine the general solution of x in the following equation:
32 tan x - 3tan x+1 = 54 (5)
[27]
QUESTION 6
In the diagram, the graphs of f (x) = -cosx +1 and g(x) = 2 sin(x + 30º) are drawn for the interval x ∈[-180º; 90º] .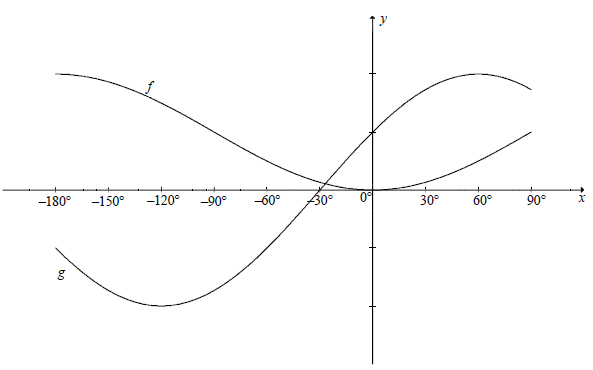
6.1 For which values of x, x ∈[-180º ; 90º] , will:
6.1.1 f(x).g(x) ≥0 (2)
6.1.2 g(x) = -1 (2)
6.2 The y-axis is moved 90° to the right. Determine the new equation of the graph originally called f , in its simplest form. (2)
[6]
QUESTION 7
In the diagram, B, C and D are in the same horizontal plane. AD is a vertical pole anchored by two cables, AB and AC. The angles of elevation from B and C to A, the top of the pole, are θ and 2θ respectively. AB = 5 units and AC = x units.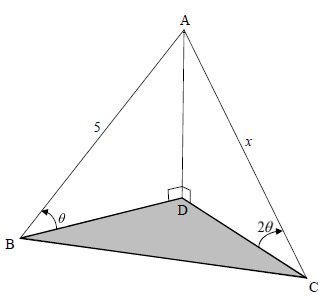
7.1 Show that x = 5 (5)
2 cos θ
7.2 Calculate the length of BC if it is given that BAC = 112º and θ = 30º. (3)
[8]
QUESTION 8
8.1 In the diagram, chords KL, LP and KP are drawn in a circle, centered at O. SLR is a tangent to the circle at L.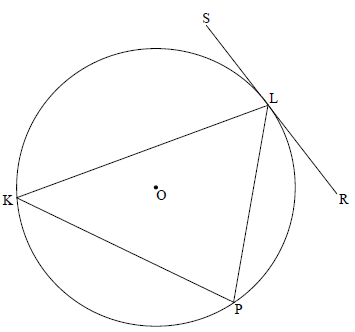
Prove the theorem which states that the angle between the tangent SLR and chord KL is equal to the angle in the alternate segment, that is prove that SLK = P. (6)
8.2 In the diagram below, PWRS is a cyclic quadrilateral in the circle, centered at O. ∆PSW is an equilateral triangle. TW is a tangent to the circle at W. Radii OR and OW are drawn. W5 = 25º.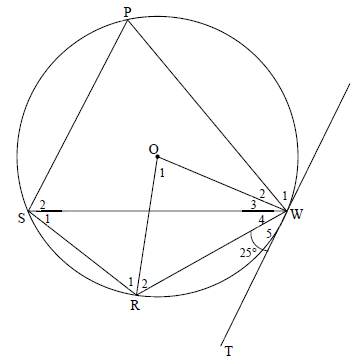
8.2.1 Determine, giving reasons, the size of:
- S1 (2)
- O1 (2)
- R1 (5)
8.2.2 Prove that SP || TW. (3)
8.3 In the diagram below, a circle centered at O is drawn. H, J, G and L are points on the circle. ∆HJL is drawn. HOG bisects JL at M.
HJ = 12√5 units and JM = 12 units.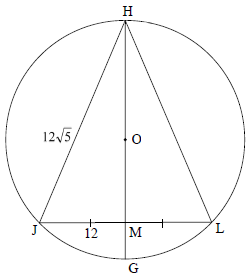
8.3.1 If MG = 6 units and OM = x, write HM in terms of x. (2)
8.3.2 Calculate, giving reasons, the length of the radius of the circle. (5)
[25]
QUESTION 9
In the diagram below, P, Q, R and S are points on a circle. PS, PQ and PR are produced to V, T and W respectively. VT || SQ and SR || VW.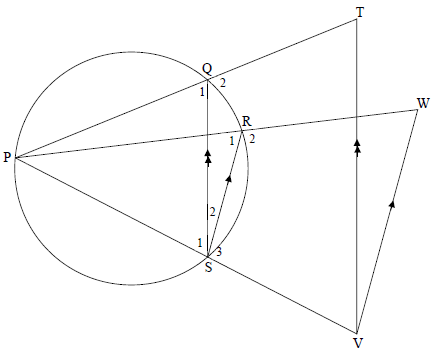
Prove, giving reasons, that:
9.1 TQ = WR (3)
QP RP
9.2 TPVW is a cyclic quadrilateral (5)
[8]
QUESTION 10
In the diagram below, B, C and D are points on a circle such that BC = CD. EC and ED are tangents to the circle at C and D respectively. BC produced meets tangent DE produced at F. B = x .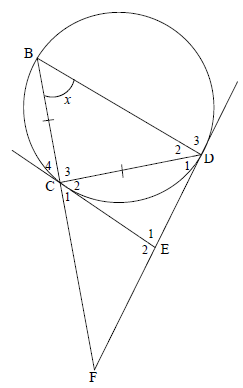
10.1 Prove, giving reasons, that:
10.1.1 E1 = 180º - 2x (5)
10.1.2 ∆ECD ||| ∆CBD (3)
10.2 Prove, giving reasons, that:
10.2.1 CD2 = CE.BD (3)
10.2.2 CF2 = BD (6)
EF2 DE
[17]
TOTAL: 150
INFORMATION SHEET