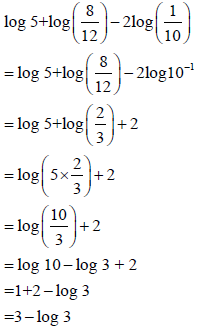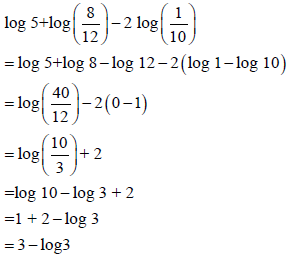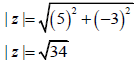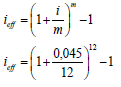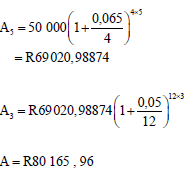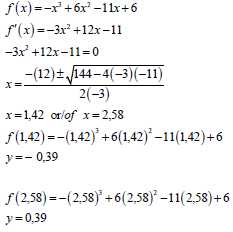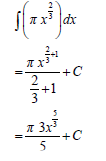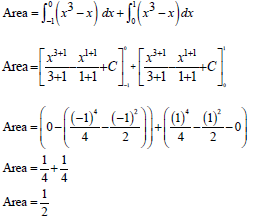Adele
Tourism Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
Read the instructions carefully before answering the questions.
- This question paper consists of FIVE sections.
- ALL questions in SECTIONS A, B, C, D and E are COMPULSORY.
- Start EACH QUESTION on a NEW page.
- You may use a non-programmable pocket calculator.
- In QUESTIONS 3.1, 3.2, 3.3.1 and 3.3.2, round off your answer to TWO decimal places.
- Show ALL calculations.
- Write neatly and legibly.
- The following table is a guide to help you allocate your time according to each section.
SECTION | QUESTION | TOPIC | MARKS | TIME (minutes) |
A | 1 | Short Questions | 40 | 20 |
B | 2 | Map Work and Tour Planning | 50 | 50 |
3 | Foreign Exchange | |||
C | 4 | Tourism Attractions | 50 | 50 |
5 | Culture and Heritage Tourism | |||
6 | Marketing | |||
D | 7 | Tourism Sectors | 30 | 30 |
8 | Sustainable and Responsible Tourism | |||
E | 9 | Domestic, Regional and International Tourism | 30 | 30 |
10 | Communication and Customer Care | |||
TOTAL | 200 | 180 | ||
QUESTIONS
SECTION A: SHORT QUESTIONS
QUESTION 1
1.1 Four options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1.1–1.1.20) in the ANSWER BOOK, for example 1.1.21 A.
1.1.1 The time in Japan when it is 16:00 on 1 June in South Africa.
- 11 pm
- 23h00
- 23:00
- 11 o’clock at night
1.1.2 In 2022, … will be the first Middle East nation and also the smallest country to host a FIFA World Cup.
- Iraq
- Qatar
- Israel
- Jordan
1.1.3 When applying for a visa, one must submit a … to the authorities of the country you want to visit.
- completed application form and confirmation of employment
- completed application form and details of family members that have visited the country in the last five years
- passport and family history
- colour photos and DHA 73 form
1.1.4 Examples of political situations:
- Civil wars and natural disasters
- Accidents and outbreaks of disease
- Terrorism and recessions
- General unrest and terrorism
1.1.5 A South African traveller will apply for a Schengen visa when wanting to visit …
- Zambia.
- Italy.
- Australia.
- Canada.
1.1.6 According to UNESCO’s criteria, the Cradle of Humankind …
- represents a masterpiece of human creative genius.
- is an outstanding example of a type of building.
- represents major stages of earth's history.
- bears a unique testimony to a civilisation which has disappeared.
1.1.7 An IDP …
- is a line of longitude that is found at 180°.
- stands for In Depth Profile and is used by travel agents to determine the needs, wants and preferences of a tourist.
- validates the bearer’s driver’s licence in a foreign country.
- allows a traveller access into a foreign country.
1.1.8 The form of payment below …
- is mostly used to make smaller purchases.
- is PIN protected and not linked to a bank account.
- takes place over a computerised network, from one bank account to another.
- does not allow for the monies received to be cashed.
1.1.9 A tourism business that offers bursaries to previously disadvantaged learners is an example of …
- BBBEE.
- local procurement.
- Triple Bottom Line.
- CSI.
1.1.10 The Vatican City is …
- a place of prayer and pilgrimage sacred to the Jewish people.
- the spiritual centre for followers of the Catholic Church.
- the oldest Islamic monument in the world.
- a famous Roman palace.
1.1.11 Tourists that learn a few words in a foreign language prior to visiting the country in which the language is spoken are practicing …
- CSI.
- Fair Trade Tourism.
- responsible tourism.
- sustainable tourism.
1.1.12 One of South Africa’s biggest travel, outdoor and adventure events:
- Comrades Marathon
- Indaba
- Getaway Show
- WTM Africa
1.1.13 Considerations for management when planning the professional image of their business:
- Stationery, customer service policies, staff cell phone policy
- Logo, staff relaxation area, slogan
- Appearance of the business, age of staff, location of staff restaurant
- Slogan and logo, stationery, appearance of the business
1.1.14 The damage caused by a(n) … is shown in the image below.
- earthquake
- bushfire
- drought
- volcanic eruption
1.1.15 A travel related disease that cannot be prevented by vaccination:
- Malaria
- Yellow fever
- Hepatitis A
- Measles
1.1.16 The Richtersveld Cultural and Botanical Landscape World Heritage Site is owned and managed by the … community.
- Nama
- San
- Damara
- Himba
1.1.17 A commercial bank exchanging ZAR for GBP for a South African traveller prior to his departure will use the:
- GDP
- BSR
- BBR
- EFT
1.1.18 The core business of SATourism:
- Crime prevention
- Co-ordinate the marketing efforts of role-players in the tourism industry
- Co-ordinate the upkeep of attractions
- Provide training for tour guides
1.1.19 An example of goods that are regarded by South African customs as restricted goods:
- One month’s supply of pharmaceutical drugs or medicines for personal use accompanied by a doctor’s prescription
- 150 cigarettes
- 1ℓ wine
- A 50 mℓ bottle of perfume
1.1.20 South Africa’s current brand slogan:
- “Nothing is more fun”
- “Inspiring new ways”
- “It’s possible”
- “Yours to explore” (20 x 1) (20)
1.2 Choose the term/concept provided in the list below that best completes the descriptions. Write only the term/concept next to the question numbers (1.2.1–1.2.5) in the ANSWER BOOK.
| Repeat visits; Market share; Credit card; The Parthenon; CCTV cameras; Cash; Colosseum; Multiplier effect |
1.2.1 The percentage of foreign arrivals in a country.
1.2.2 The best form of payment for a tourist when using a taxi.
1.2.3 A Roman arena used for public events.
1.2.4 A factor contributing to the success of a tourist attraction.
1.2.5 A characteristic of a successful tourist attraction. (5 x 1) (5)
1.3 Choose the correct word(s) from those given in brackets. Write only the word(s) next to the question numbers (1.3.1–1.3.5) in the ANSWER BOOK.
1.3.1 A traveller entering South Africa, carrying a package for a friend that was packed by the friend’s mother, should choose the (red/green) channel on arrival at customs.
1.3.2 Daylight savings time is practiced in certain countries by adjusting their clocks ONE hour ahead in the (winter/summer) months.
1.3.3 (Jet lag/jet fatigue) is a travel related condition caused by flying for many hours in an airplane.
1.3.4 (India/Central Africa) is a yellow fever endemic area.
1.3.5 A passport issued to a South African citizen at the age of 12 years is valid for (10/5) years from the date of issue. (5 x 1) (5)
1.4 Choose a(n) attraction/destination from COLUMN B that matches the description in COLUMN A. Write only the letter (A–G) next to the question numbers (1.4.1–1.4.5) in the ANSWER BOOK, for example 1.4.6 H.
COLUMN A | COLUMN B | ||
1.4.1 | A huge limestone statue located in Giza, Egypt | A | ǂKhomani Cultural Landscape |
1.4.2 | A symbol of the division between democracy and communism during the Cold War | B | Baberton Makhonjwa Mountains |
1.4.3 | Located at South Africa’s border with Botswana and Namibia | C | The Sphinx |
1.4.4 | Located at the summit of Mount Corcovado, Rio de Janeiro, Brazil | D | Vredefort Dome |
1.4.5 | A prosperous African kingdom dating from 1 000 years ago | E | Statue of Christ the Redeemer |
F | The Berlin Wall | ||
G | Mapungubwe Cultural Landscape | ||
(5 x 1) (5)
1.5 Rearrange the steps in the correct order for an inbound international tourist arriving at OR Tambo International Airport (ORTIA) in South Africa. Write only the letters, A–E, in the ANSWER BOOK.
(5 x 1) (5)
TOTAL SECTION A: 40
SECTION B:
MAP WORK AND TOUR PLANNING; FOREIGN EXCHANGE
QUESTION 2
2.1 Use the world time zone map and the scenario to answer the questions.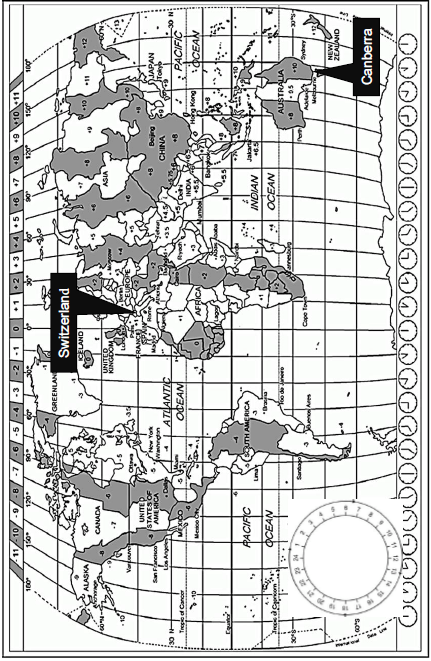

2.1.1 Calculate the time and date that the USA Secretary of Health, Mr Xavier Becerra, logged into the online press conference from his office in Washington DC, the capital of the United States of America. NOTE: Show ALL calculations. (4)
2.1.2 Calculate the time and date that the Australian Minister of Health, The Honourable Greg Hunt, logged into the online press conference from his offices in Canberra, the capital of Australia. Remember that Australia was practicing Daylight Savings Time at the time of the online press conference.
NOTE: Show ALL calculations. (5)
2.1.3 South Africa joined the rest of the world in sourcing Covid-19 vaccinations. The first batch of vaccinations was placed on an Air Emirates flight that departed from Chhatrapati Shivaji Maharaj International Airport in Mumbai, India en route to OR Tambo International Airport, Johannesburg, South Africa on 31 January 2021.
The flight pattern is given below.
Depart 04:30 | Chhatrapati Shivaji Maharaj International Airport – Mumbai, India | |
Arrive 06:00 | Dubai International Airport – Dubai, United Arab Emirates | |
| Layover: 3 hrs 55 min | ||
Depart 09:55 | Dubai International Airport – Dubai, United Arab Emirates | |
Arrive: | OR Tambo International Airport – Johannesburg, South Africa | |
| Total flying time 15 hrs 15 min | ||
- Calculate the date and time of arrival of the flight at OR Tambo International Airport, Johannesburg, South Africa.
NOTE: Show ALL calculations. (6) - The crew of the Air Emirates flight that transported the vaccinations to South Africa suffered from jet lag on their arrival.
List THREE symptoms of this travel related condition. (3) - The crew of the Air Emirates flight will be required to pass through customs control with their personal luggage on their arrival in South Africa.
Explain the function performed by customs control. (2)
2.2 Study the image and text and answer the questions that follow.
2.2.1 Identify the compulsory travel document in the image above. In your answer, refer to the letters A, B or C. (2)
2.2.2 Explain the use of the travel document labelled C. (2)
2.2.3 Due to the travel restrictions resulting from the Covid-19 pandemic, some countries are considering implementing vaccine passports. This is a digital certificate stored on the travellers’ smartphone, showing proof of vaccination and permits them to travel. Discuss TWO advantages of a traveller being in possession of a vaccine passport when travelling internationally. (4)
2.3 Read the extract and answer the questions.
2.3.1 Identify the type of tourist that would attend a Covid-19 compliant conference at one of Tsogo Sun’s hotels. (1)
2.3.2 Suggest TWO Covid-19 safety measures that the conference organiser at Tsogo Sun must have in place. (4)
[33]
QUESTION 3
Study the exchange rate table below and answer the questions that follow.
Country | Currency code | BBR | BSR |
Italy | EUR | 16,39 | 16,98 |
England | GBP | 19,06 | 19,77 |
USA | USD | 13,54 | 13,87 |
3.1 A South African business owner is planning a business trip to Rome, Italy. He has R45 000 to exchange for his expenses during the trip.
Calculate the number of Euro’s that he will receive when he exchanges his R45 000.
NOTE: Round off your answer to TWO decimal places. Show ALL the steps of your calculation. (3)
3.2 Upon his return to South Africa, the business owner has €23 left over from his trip. Calculate how much he will receive in Rand when he exchanges the €23.
NOTE: Round off your answer to TWO decimal places.
Show ALL the steps of your calculation. (3)
3.3
Siya is a top Grade 12 academic achiever at his school in the Eastern Cape. When he finishes school, he wants to study medicine and has been saving money for many years. He has R175 000 saved for spending money. He has applied to, and been accepted at, both the University of California, USA and the University of Oxford, England. |
3.3.1 Calculate how much Siya will receive in USD if he exchanges R175 000 in preparation for his trip. NOTE: Round off your answer to TWO decimal places.
Show ALL the steps of your calculation. (3)
3.3.2 Calculate how much Siya will receive in GBP if he exchanges R175 000 in preparation for his trip. NOTE: Round off your answer to TWO decimal places.
Show ALL the steps of your calculation. (3)
3.3.3 Determine which country will allow Siya to have more spending money while he is studying medicine. (1)
3.4 Study the image and answer the question that follows.
Discuss the impact of the decline of the value of the Rand in relation to the US Dollar on international inbound tourists from the United States of America to South Africa. (2 x 2) (4)
[17]
TOTAL SECTION B: 50
SECTION C:
TOURISM ATTRACTIONS; CULTURE AND HERITAGE TOURISM; MARKETING
QUESTION 4
4.1 Study the travel vision board (a collage of all the places that you would like to travel to) that you created with images of world icons and answer the questions that follow.
4.1.1
Give the official names of the icons labelled A to F on your travel vision board. (6)
4.1.2 Provide the following information about your travel vision board:
- The number of continents that you will visit. (2)
- The name of the country featuring TWO icons. (2)
- ONE nature-based activity you will participate in when visiting the icon labelled A. (2)
4.2 Study the information on Venice and answer the questions that follow.
In pre-Covid-19 times, Venice, with an estimated population of 54 000, welcomed more than 30 million tourists each year, (±60 000 to 80 000 tourists per day) half of them being day visitors. From April to October, cruise ships flooded the city spilling ±32 000 passengers onto the narrow streets daily. The overcrowding resulted in a poor environment for locals as well as visitors. [Adapted from https://edition.cnn.com & www.thelocal.it] |
4.2.1 Identify the main problem caused by tourism that the city authorities in Venice must manage. (2)
4.2.2 Give ONE reason why Venice is a popular icon. (2)
4.2.3 Suggest TWO factors that led to the decision by the city authorities to act against fast-food outlets in Venice. (2 x 2) (4)
4.2.4 Discuss TWO environmental benefits that will result from the ban on large cruise ships. (2 x 2) (4)
[24]
QUESTION 5
Study the image of a South African World Heritage Site and answer the questions that follow.
5.1 Identify the World Heritage Site in the image. (2)
5.2 Name the province in which a tourist must be to visit the World Heritage Site. (2)
5.3
| UNESCO, in partnership with the African World Heritage Fund periodically runs a #MyAfricanHeritage Instagram competition for young people between the ages of 18 and 32. Participants are required to upload their pictures or videos of an African UNESCO World Heritage Site using the hashtag #MyAfricanHeritage. The posted pictures or videos must show the unique character of an African UNESCO World Heritage Site to stand a chance to win one of the prizes. |
5.3.1 You decide to enter the competition and arrange with your family to visit the World Heritage Site shown in the image above. Name THREE types of landforms you photographed to show the geographical diversity of the World Heritage Site. (3 x 2) (6)
5.3.2 Suggest TWO ways in which UNESCO’s African World Heritage Site Instagram competition will add value to South Africa's tourism industry. (2 x 2) (4)
[14]
QUESTION 6
Study the extracts below and answer the questions that follow.
6.1 Identify the source market targeted by SATourism in its Twitter marketing campaign. (2)
6.2 SATourism #MeetSouthAfrica marketing campaign was renamed to #MeetSouthAfricaLater due to the Covid-19 pandemic international travel restrictions.
Suggest TWO reasons behind SATourism’s Twitter post of 31 May 2020. (2 x 2) (4)
6.3
The WTM is the leading global event for the travel industry to meet industry professionals and conduct business deals. |
Explain how SATourism is funded to market South Africa as a tourism destination of choice at the WTM. (3 x 2) (6)
[12]
TOTAL SECTION C: 50
SECTION D:
TOURISM SECTORS; SUSTAINABLE AND RESPONSIBLE TOURISM
QUESTION 7
Read the newspaper article and answer the questions that follow.
Cabin crew member takes well known South African airline to court for unfair dismissal.
Susan Smith, cabin crew member for Penika Airways, has taken the airline to court for unfair dismissal after she was fired after falling asleep on a flight from Port Elizabeth to Johannesburg. Smith claims that she had to work a 14-hour shift without a break after two of her colleagues became ill and could not do their shifts. |
7.1 Name the contract that Susan would have signed when she was employed by Penika Airways. (1)
7.2 State ONE reason why it is important for employees to sign the contract mentioned in QUESTION 7.1. (2)
7.3 Identify the document that Susan contravened (disobeyed) when she acted in an unprofessional manner (way) complaining to the passengers about her working hours. (1)
7.4 List TWO reasons why a business should have the document referred to in QUESTION 7.3. (2 x 2) (4)
7.5 Give your opinion about the validity of the statement by the CEO of Penika Airways, Themba Njengane, about Susan’s unprofessional behaviour. (2)
7.6 Airline cabin crew members work in a demanding (challenging) environment. Give ONE reason to support this statement. (2)
[12]
QUESTION 8
Read the scenario and answer the questions that follow.
Responsible Environmental Management at Mashovhela Lodge Morning Sun Nature Reserve is a National Heritage Site, noted for its unique biodiversity, located in the Soutpansberg Mountains in Limpopo Province. Management at Mashovhela Lodge are aware of their responsibility to conserve the diversity and natural beauty of the reserve for future generations and to educate as many people as possible about protecting our planet.
Here are some ways in which Mashovhela Lodge avoids damage to the environment and embraces eco-friendly principles:
[Adapted from www.morningsun.co.za] |
8.1 List TWO of the SIX principles of Fair-Trade Tourism. (2)
8.2 Discuss the value of a Fair-Trade accreditation (certification) for Mashovhela Lodge. (4)
8.3 Suggest ONE strategy, under each of the following headings, that Mashovhela Lodge can implement to maintain (continue) their commitment to responsible environmental management:
8.3.1 Waste management (2)
8.3.2 Water supply (2)
8.3.3 Renewable energy (2)
8.4 Explain ONE reason why Mashovhela Lodge should educate people about protecting our planet. (2)
8.5 Sustainable tourism encompasses more than ensuring that the environment is well looked after. Suggest ONE manner whereby Mashovhela Lodge can ensure that they uphold the following pillars of sustainable tourism:
8.5.1 Social pillar (2)
8.5.2 Economic pillar (2)
[18]
TOTAL SECTION D: 30
SECTION E:
DOMESTIC, REGIONAL AND INTERNATIONAL TOURISM; COMMUNICATION AND CUSTOMER CARE
QUESTION 9
9.1 Study the extract and images below and answer the questions that follow.
G7 SUMMIT IN CORNWALL, UNITED
The seaside resort of Carbis Bay in the county (district) of Cornwall, with a population of around 4 000, has been chosen to be the main venue of the G7 summit to be held from 11 to 13 June 2021. The village will be supported by St Ives and Falmouth, along with other towns across the region.
Hosting the G7 summit in Cornwall will provide a fantastic opportunity to showcase the region on the world stage, local leaders have said. [Adapted from www.bbc.com] |
9.1.1 Explain ONE reason that influenced local leaders to make the statement: “Hosting the G7 summit in Cornwall will provide a fantastic opportunity to showcase the region on the world stage”. (2)
9.1.2 Suggest TWO incidents (happenings) that would have disrupted the lives of the residents in the weeks and days leading up to, as well as during the G7 summit. (2 x 2) (4)
9.1.3 The global recovery from the Covid-19 pandemic was one of the main discussion points at the G7 Summit. In a paragraph, discuss THREE ways in which this unforeseen occurrence negatively impacted the international tourism economy. (3 x 2) (6)
9.2 Study the statistics below and answer the questions that follow.
What do international visitors spend their money on while in South Africa? |
Percentage breakdown of total expenditure by product ranked from highest to lowest (2005 – 2017) |
Total spend in 2005 = R51 billion. Total spend in 2017 = R151 billion. |
|
*Non-specific products: These are products that visitors buy that are not specifically related to tourism activities. Retail (‘shopping’) products fall into this category. |
[Source: www.statssa.gov.za] |
9.2.1 State the increase in the total amount of international visitor spend that contributed to the South African economy in 2017 compared to 2005. (2)
9.2.1 Identify the year in which the air transport spend item for international visitors reached its highest ranking. (2)
9.2.3 Recommend TWO ways in which tourism businesses can increase the spend by international tourists. (4)
[20]
QUESTION 10
Study the extract below and answer the questions that follow.
10.1 Identify the customer feedback method used in the extract above. (2)
10.2 Give ONE benefit for consumers reading service delivery reviews on the Hellopeter platform. (2)
10.3 Suggest THREE negative impacts for the business because of the TikaThai management not following through on the intervention plan they posted on the Hellopeter platform. (3 x 2) (6)
[10]
TOTAL SECTION E: 30
GRAND TOTAL: 200
Technical Sciences Paper 2 Memorandum - Grade 12 September 2021 Preparatory Exams
MEMORANDUM
QUESTION 1
1.1 C (2)
1.2 C (2)
1.3 D (2)
1.4 C (2)
1.5 D (2) [10]
QUESTION 2
2.1 Functional group (1)
2.2 Macromolecule (1)
2.3 Semiconductor (1)
2.4 Electrolysis (1) [4]
QUESTION 3
3.1 Doping is the process of adding impurities to an intrinsic semiconductor to improve its conductivity. (2)
3.2
- Silicon is a pure semiconductor, as impure atoms must be added to improve conductivity.
OR - A pure semiconductor which is undoped.(2)
3.3 3.3.1 P-type semiconductor/P-tipe halfgeleier (1)
3.3.2 A diode allows the current to flow in one direction only. (1)
[6]
QUESTION 4
4.1 4.1.1 C OR G (1)
4.1.2 A (1)
4.1.3 A AND E (2)
4.1.4 B (1)
4.1.5 E (1)
4.2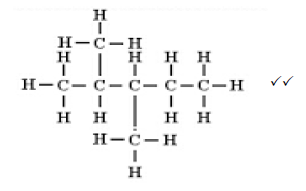 (2)
(2)
4.3 4.3.1 Addition(1)
4.3.2 HBr (1)
4.4 Pentanoic Acid and Ethanol (2)
[12]
QUESTION 5
5.1 A series of organic molecules that is defined by the same general formula and where each member differs from the next by a CH2 group. (2)
5.2
- An increase in the number of branched chains results in a decrease in the boiling point.
OR - Straight chain alkanes have a higher boiling point compared to their corresponding branched chains. (1)
5.3
- Straight-chained molecules can get closer to one another than branched molecules and have larger surface area in contact for intermolecular forces to form, therefore the Van der Waals forces/london forces are stronger. hence more energy is required to overcome intermolecular forces between the straight chain molecules compared to branched chains. therefore, straight-chained molecules have a higher boiling point.
OR - Branched chains form molecules that are more spherical with fewer points of contact for intermolecular forces. Therefore, the Van der Waals forces / London forces are weaker. Hence less energy is required to overcome intermolecular forces between the branched chains compared to straight chains, thus a lower boiling point. (4)
5.4 The learner should:
- Avoid direct heating with an open flame.
- Work in a well-ventilated area. Any one
- Use a fume hood.
Reason: Alkanes are fuels and are highly flammable (2)
[9]
QUESTION 6
6.1
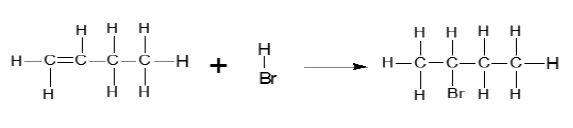 (4)
(4)
MARKING CRITERIA
- Correct structure of reactants. (2)
- Correct structure of the product(2)
6.2 Hydrohalogenation/addition. (1)
6.3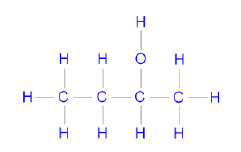
Butan-2-ol (2-butanol) (3)
6.4 Hydrolysis (1)
6.5
6.5.1 Water (1)
6.5.2 H2SO4 / HCℓ / H3PO4 (1)
6.5.3 Hydration (Accept: Addition) (1)
6.6
- Manufacturing of plastic bags (Any one )
- Synthesis of bullet proof vests
- Manufacturing of squeeze bottles
- Manufacturing of cling wrap (1)
[13]
QUESTION 7
7.1
- An electrolyte is a substance of which the aqueous solution contains ions.
OR - A substance that dissolves in water to give a solution that conducts electricity.
OR - A substance that forms free ions when melted. (2)
7.2 Electrolytic cell (1)
7.3
7.3.Cu2+ (aq) + 2e– → Cu (s) (1)
7.3.2 2Cl- (aq) → Cl2(g) + 2e- (1)
7.4 Chlorine (1)
7.5 Conversion of electrical energy to chemical energy. (1)
[7]
QUESTION 8
8.1
- Salt bridge. It maintains electrical neutrality.
OR - It separates the two compartments so that they do not mix. (2)
8.2 Chemical energy is converted into electrical energy. (1)
8.3 It is a non-spontaneous reaction. (1)
8.4
8.4.1
- Eᶿcell = Eᶿcathode - EᶿAnode
= -0,74 – (-0,76)
= 0,02 V
OR - Cr3+ +3e- → Cr Eθ= -0,74
Zn →Zn2+ +2e- Eθ = +0,76
Eθcell = 0,02 V (3)
8.4.2 Decreases (1)
8.5 Measurements are not done under standard conditions of temperature at 25 °C and concentration of electrolytes of 1 mol·dm-3. (2)
8.6
8.6.1 Fuel cell/Brandstofsel (2)
8.6.2 It increases energy security, improves the quality of air and the environment. (ANY ONE ) (1)
8.6.3 More expensive than petroleum.
- Not suitable for use in low temperatures. (Any one)
- Could harm rubber hoses of some engines.
- Can contribute to food shortage. (1)
[14]
TOTAL: 75
Technical Sciences Paper 2 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
- Write your FULL NAME and SURNAME in the appropriate spaces in the ANSWER BOOK.
- Answer ALL the questions.
- Start each question on a NEW page in the ANSWER BOOK.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Number the answers according to the numbering system used in this question paper.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your final numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions et cetera where required.
- You are advised to use the attached DATA SHEETS.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1−1.5) in the ANSWER BOOK, for example 1.6 D.
1.1 A diode can convert …
- an electrical current to potential difference.
- potential difference to heat.
- an alternating current to a pulsating direct current.
- an electrical current to light. (2)
1.2 Which ONE of the following is a general formula of alkanes?
- C2nHn+2
- CnH2n
- CnH2n+2
- C2H2n (2)
1.3 Sharon, a Grade 12 Technical Sciences learner, left a solution of copper sulphate in a zinc container overnight. Early the next morning she noticed a brown insoluble substance coating the inside, around the sides and bottom of the zinc container. The container was corroded and some of the solution had leaked to the floor.
Which ONE of the following reactions took place inside the zinc container?
- Cu(s) + ZnSO4(aq) → CuSO4(aq) + Zn(s)
- Cu2+(aq) + ZnSO4(aq) → CuSO4(aq) + Zn(s)
- Zn2+(aq) + CuSO4(aq) → ZnSO4(aq) + Cu2+(aq)
- Zn(s) + CuSO4(aq) → ZnSO4(aq) + Cu(s) (2)
1.4 The diagram below represents a part of an electrochemical cell used for the electroplating of copper. The impure copper contains silver metal and zinc metal.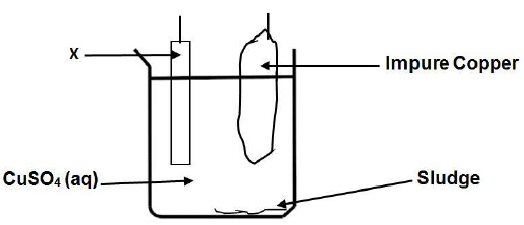
Which ONE of the following half-reactions will take place at electrode X?
- Ag+ + e- → Ag
- Cu → Cu2+ + 2e-
- Cu2+ + 2e- → Cu
- Zn2+ + 2e- → Zn (2)
1.5 Which ONE of the following reactions is spontaneous under standard conditions?
- Sn4+ + SO2 + 2H2O → Sn2+ + SO42- + 4H+
- I2 + 2Br - → 2I- + Br2
- 2H2O → O2 + 2H2
- 2Ag+ + Fe2+ → 2Ag + Fe3+ (2)
[10]
QUESTION 2 (Start on a NEW page.)
Give ONE word for each of the phrases given below.
2.1 An atom or group of atoms that determine the chemistry of a molecule (1)
2.2 A molecule that consists of a large number of atoms (1)
2.3 A material that has electrical conductivity between that of a conductor and an insulator(1)
2.4 The decomposition of a substance when an electric current passes through it (1)
[4]
QUESTION 3 (Start on a NEW page.)
Semiconductor devices such as diodes and transistors are widely used in modern electronics.
3.1 Define the term doping in words. (2)
3.2 Silicon is listed as an intrinsic semiconductor. Explain the meaning of an intrinsic semiconductor. (2)
3.3 A learner in a school laboratory adds boron to pure silicon to make it a better conductor of electricity.
3.3.1 Which type of semiconductor does this learner manufacture during the process above? (1)
3.3.2 A diode is a simple semiconductor device. How does a diode conduct electric current? (1)
[6]
QUESTION 4 (Start on a NEW page.)
Study the organic compounds represented by the letters A to G in the table below.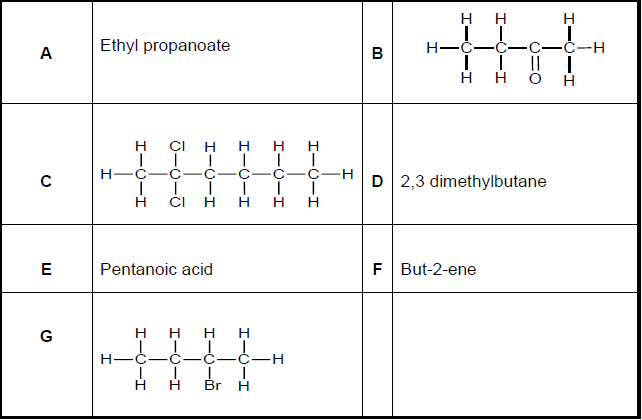
4.1 Write down the LETTER(S) that represent(s) each of following: (A compound may be used more than once.)
4.1.1 An alkyl halide (1)
4.1.2 An ester (1)
4.1.3 Two compounds that are structural isomers (2)
4.1.4 A ketone (1)
4.1.5 A compound containing a carboxyl group (1)
4.2 Write down the structural formula of compound D. (2)
4.3 Compound G is formed from compound F.
4.3.1 Name the type of reaction that produces compound G. (1)
4.3.2 Give the FORMULA of the other compound that reacted with compound F to form compound G. (1)
4.4 Give the IUPAC NAMES of the TWO compounds that will react to form compound A. (2)
[12]
QUESTION 5 (Start on a NEW page.)
A learner investigates the relationship between the structural isomers of pentane and their boiling points. The results obtained were recorded as shown below:
COMPOUND | MOLECULAR FORMULA | BOILING POINT (°C) | |
Pentane | C5H12 | 36 | |
2-methylbutane | C5H12 | 28 | |
2,2-dimethylpropane | C5H12 | 10 | |
5.1 Define the term homologous series. (2)
5.2 For this investigation, write down the conclusion that can be drawn from the above results. (1)
5.3 Refer to MOLECULAR STRUCTURE, INTERMOLECULAR FORCES and ENERGY needed, to explain your conclusion in QUESTION 5.2. (4)
5.4 What precaution should the learners take when carrying out this experiment? Give a reason for your answer. (2)
[9]
QUESTION 6 (Start on a NEW page.)
In industry, alkenes are used in the synthesis of a variety of organic compounds. The flow diagram below illustrates some of the many possible reactions.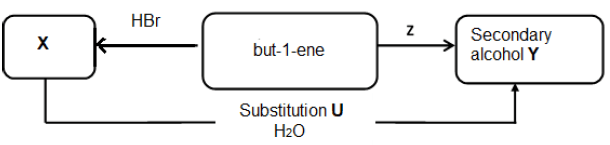
6.1 Use structural formulae to indicate the reaction for the formation of compound X. (4)
6.2 Name the type of reaction that takes place when but-1-ene is converted to compound X. (1)
6.3 Write down the structural formula and IUPAC name of the secondary alcohol Y that is formed. (3)
6.4 Name the type of substitution reaction U that takes place when compound X is converted to the secondary alcohol Y. (1)
6.5 With the aid of a catalyst, but-1-ene can be converted directly to the secondary alcohol, without the formation of the intermediate compound X.
6.5.1 Besides but-1-ene, write down the NAME of the other reactant needed for reaction Z. (1)
6.5.2 Write down the FORMULA of the catalyst that can be used. (1)
6.5.3 Name the type of reaction Z that will take place during this direct conversion. (1)
6.6 Give ONE industrial use of polyethylene. (1)
[13]
QUESTION 7 (Start on a NEW page.)
The diagram below represents an electrochemical cell used to decompose a concentrated copper(II) chloride solution using inactive electrodes.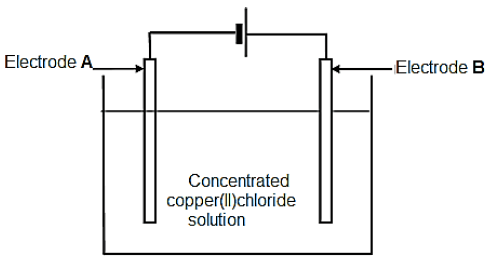
When the cell is functioning, a gas is released at electrode A, whilst electrode B is coated with a reddish brown layer.
7.1 Define the term electrolyte. (2)
7.2 What type of an electrochemical cell is represented above? (1)
7.3 Write down a half-reaction to explain the observation made at:
7.3.1 Electrode A (1)
7.3.2 Electrode B (1)
7.4 Write down the NAME of the gas formed while the cell is functioning. (1)
7.5 What energy conversion is taking place in this type of electrochemical cell? (1)
[7]
QUESTION 8 (Start on a NEW page.)
A Grade 12 Technical Sciences learner receives an assignment to arrange some metals according to their reducing ability. He sets up the electrochemical cell shown in the diagram below.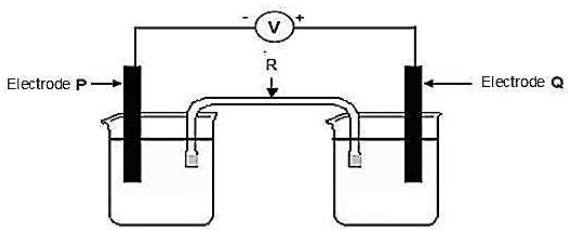
The learner uses different metals as electrodes. He records the following results:
COMBINATION | ELECTRODE P | ELECTRODE Q | VOLTMETER READING (V) |
1 | Chromium | Silver | +0,3 |
2 | Silver | Zinc | -0,7 |
3 | Zinc | Copper | 0,8 |
8.1 Write down the name of the component labelled R and give ONE function of this component. (2)
8.2 Write down the energy conversion that takes place in this cell when it is in operation. (1)
8.3 Give a possible reason why the voltmeter reading for the silver-zinc cell is negative. (1)
8.4 Consider the ZINC-CHROMIUM CELL represented by the notation below:
Zn(s)/Zn2+(aq, 1 mol·dm-3)//Cr3+ (aq, 1 mol·dm-3) /Cr(s)
8.4.1 Use the table of Standard Reduction Potentials to determine the initial potential difference (emf) of this cell under standard conditions. (3)
8.4.2 How will the initial voltmeter reading be affected if the concentration of the electrolyte in the Zn(s)/Zn2+(aq) half-cell is increased? Write down only INCREASES, DECREASES, or REMAINS THE SAME. (1)
8.5 The learner notices that the measured value represented in the table and the calculated (emf) in QUESTION 8.4.1 differ. Give TWO possible reasons for this difference in values. (2)
8.6 Modern biodiesel fuel which is made by converting vegetable oils into compounds called fatty acid methyl esters, has its roots in research conducted in the 1930s in Belgium, but today’s biodiesel industry was not established in Europe until the late 1980s.
8.6.1 Give TWO other alternate energies except biodiesel in Technical Sciences. (2)
8.6.2 What is the environmental impact of using alternative energies? (1)
8.6.3 Give ONE disadvantage of using biodiesel as a fuel. (1)
[14]
TOTAL: 75
NATIONAL SENIOR CERTIFICATE
DATA FOR TECHNICAL SCIENCES GRADE 12 PAPER 2 (CHEMISTRY)
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Avogadro’s constant | NA | 6,02 × 1023 mol-1 |
Molar gas constant | R | 8,31 J.K-1.mol-1 |
Standard pressure | pq | 1,013 × 105 Pa |
Molar gas volume at STP | Vm | 22,4 dm3∙mol-1 |
Standard temperature | Tθ | 273 K |
TABLE 2: FORMULAE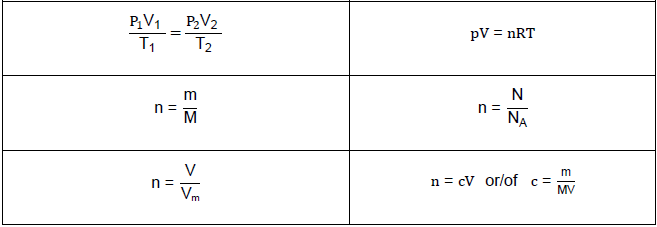
TABLE 3:THE PERIODIC TABLE OF ELEMENTS
TABLE 4A: STANDARD REDUCTION POTENTIAL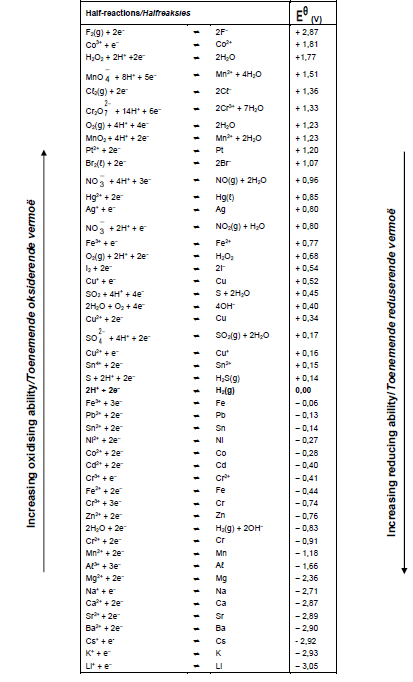
TABLE 4B:STANDARD REDUCTION POTENTIALS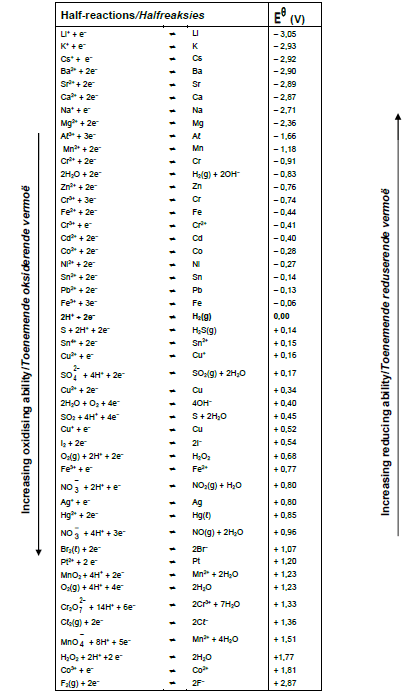
Technical Sciences Paper 1 Memorandum - Grade 12 September 2021 Preparatory Exams
MEMORANDUM
QUESTION 1
1.1 D (2)
1.2 D (2)
1.3 A (2)
1.4 B (2)
1.5 C (2)
1.6 A (2)
1.7 C (2)
1.8 A (2)
1.9 A (2)
1.10 C (2)
[20]
QUESTION 2
2.1 F Net force
2.2 A Impulse
2.3 G Stress
2.4 B Thrust
2.5 C Optic axis
2.6 I Electric motor
2.7 E Tension
2.8 D Capacitor (8 x 1) [8]
QUESTION 3
3.1
Action force | Reaction force | |
3.1.1 | Weight of the boy | Force of boy on the earth ? |
3.1.2 | Normal force of ground on the trolley | Force of the trolley on the ground.? |
3.2 West (1)
3.3 When object A exerts a force on object B, object B simultaneously exerts an oppositely directed force of equal magnitude on object A. (2)
[5]
QUESTION 4
4.1 When a non-zero resultant force acts on an object, the object accelerates in the direction of the resultant force. This acceleration is directly proportional to the resultant force and inversely proportional to the mass of the
object. (2)
4.2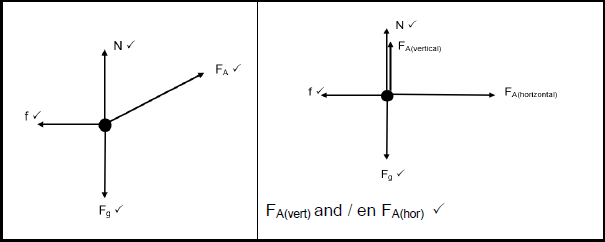 (4)
(4)
4.3
- fk = µkN
fk = (0,2)(473,28)
fk = 94,66 N Fg = N + Fv
(60)(9,8) = N + 200 sin 35°
N = 473,28 N (4)
4.4
- Fnet = ma
FA(hor) + fk = ma
(200 cos 350) + (- 94,66) = (60)(a)
a = 1,15 m.s-2 (3)
4.5 Decreases
Fhorizontal of 200 N and fk decrease as the angle increases.
Decrease in Fhorizontal is greater than decrease in fk.
∴ Fnet decreases.
Fnet α a (3)
[16]
QUESTION 5
5.1
5.1.1 Yes (1)
5.1.2
- pi = mv = 20 000 kg.m.s-1
K = ½mv2 = 200 000 J
½(mv)v = 200 000
½(20 000) v = 200 000
v = 20 m.s-1 due east (4)
5.1.3 Mark positive from Ques 5.1.2
OPTION 1 | OPTION 2 | OPTION 3 |
K = ½mv2\ | p = mv | ½mv2 = 200 000 … |
(2)
5.2
5.2.1 Total linear momentum of an isolated system remains constant. (2)
5.2.2 Right – Positive
- ∑ pi = ∑ pf Any one
∑ pi = (mP + mR)vf + mQvf 0 = (6)(2) +(3 + 2) (v)
v = 2,4 m.s-1 left / links (4)
[13]
QUESTION 6
6.1
6.1.1 Rate of transfer of energy / Rate at which work is done.(2)
6.1.2
- P = Fv
P = (300)(0,5)
P = 150 W (3)
6.1.3
OPTION 1 | OPTION 2 |
P = W | Δx = v Δt = (0,5)(50) = 25 m |
(3)
6.1.4
- 7500 J
Crate moves with constant velocity (2)
6.2
6.2.1 Total mechanical energy of an isolated system remains constant. (2)
6.2.2
- (ME)A = (ME)B
(U + K)A = (U+K)B Any one
(mgh + ½mv2)A = (mgh + ½mv2)B
(2)(9,8)(10) + 0 = 0 + ½(2)(v)2
v = 14 m.s-1 (4)
6.2.3
- (ME)A = (ME)C
(U + K)A = (U+K)B Any one
(mgh + ½mv2)A = (mgh + ½mv2)C
(2)(9,8)(10) + 0 = (2)(9,8)(h) + ½(2)(7)2
h = 7,5 m (4)
[20]
QUESTION 7
7.1 7.1.1 Hooke’s law states that, within the limit of elasticity, stress is directly proportional to the strain. (2)
7.1.2
- σ = F
A
? = 500
0,01
? = 50000 Pa (3)
7.1.3
- K = σ
ε
200× 109 = 50000
ε
ɛ = 2,5× 10-7
s = Δ?
?
2,5× 10-7 = Δ?
0,9
Δl = 2,25× 10-7 m (6)
7.1.4 Decreases (1)
7.2 As the temperature increases the viscosity decreases. (2)
7.3
7.3.1
- F1 = F2
A1 A 2
?1 = 1200×9,8
0,04 0,7
F1 = 672 N (4)
7.3.2 Hydraulic brakes / car lifts / hydraulic jacks / forklifts / dentist chairs (ANY TWO) (2)
[20]
QUESTION 8
8.1
8.1.1 Same as the object (1)
8.1.2 50 + 50 = 100 cm (2)
8.2
8.2.1 48,8° (1)
8.2.2 The ray will be totally reflected on the water. (2)
8.2.3 Total internal reflection/Totale interne weerkaatsing (1)
8.3
8.3.1 24 cm away on the other side of the lens (1)
8.3.2 20 mm (1)
8.3.3 Real (1)
8.3.4 Cameras / projectors / spectacles / lighthouse / telescope / microscope (ANY ONE) (1)
[11]
QUESTION 9
9.1 9.1.1 Gamma rays (1)
9.1.2 To sterilise medical equipment/treatment of cancer/Detection of radioactive tracers (ANY ONE) (1)
9.2 9.2.1 Wave packets/quantum packets are called photons. (2)
9.2.2
OPTION 1 | OPTION 2 |
c = fλ | E= hc |
(5) [9]
QUESTION 10
10.1
10.1.1 A capacitor is a device for storing electrical charge. (2)
10.1.2
- C = εo A
d
480 × 10-9 = 8,85×10−12×A
0,012×10-3
A = 0,65 m2 (3)
10.1.3 Decreases (1)
10.2
10.2.1
 (3)
(3)
10.2.2
 (3)
(3)
[12]
QUESTION 11
11.1 1
1.1.1 The process of generating electricity from motion. (2)
11.1.2 Galvanometer needle deflects. (1)
11.1.3 No deflection
- A current is induced only when there is a relative motion. (2)
11.2
- ε = − NΔɸ
Δ?
ε = (2)(50−38)
0,42
ε = 57,14 V (3)
[8]
QUESTION 12
12.1
12.1.1
- V? = ??
?? ??
9 = ??
230 400
Ns = 15,65 ≈ 16 (3)
12.1.2 Step down (1)
12.2
12.2.1 Electromagnetic induction / Faradays law (1)
12.2.2 Brush (1)
12.2.3 Slip rings (1)
12.2.4 Replace slip rings with a split ring commutator. (1)
[8]
TOTAL: 150
Technical Sciences Paper 1 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- Write your FULL NAME and SURNAME in the appropriate spaces on the ANSWER BOOK.
- Answer ALL the questions.
- Start each question on a NEW page in the ANSWER BOOK.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Number the answers correctly according to the numbering system used in this question paper.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, et cetera where required.
- You are advised to use the attached DATA SHEETS.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1 to 1.10) in the ANSWER BOOK.
1.1 A physical quantity that is described as a measure of the resistance of a body to a change in its state of rest or state of motion with constant velocity is called …
- momentum.
- impulse.
- energy.
- inertia. (2)
1.2 A constant net force of 2 N, to the right, acts on a box as shown below. The kinetic frictional force between the surface and the block is 2 N.
What will happen to the box?
The box will …
- not move.
- move with constant velocity to the right.
- move with constant acceleration to the left.
- move with constant acceleration to the right. (2)
1.3 The acceleration vs 1/mass graph for a body is given below.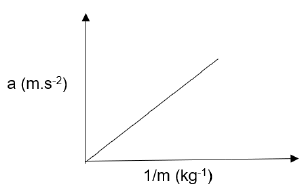
The physical quantity that is represented by the gradient of the graph is …
- net force.
- velocity.
- momentum.
- displacement. (2)
1.4 Two identical trolleys collide head on with each other. The collision is INELASTIC.
Which ONE of the following is CORRECT regarding the total momentum and the total kinetic energy of the two trolleys during the collision?
Total momentum of the two trolleys is … | Total kinetic energy of the two trolleys is … | |
A | conserved | conserved |
B | conserved | not conserved |
C | not conserved | conserved |
D | not conserved | not conserved |
(2)
1.5 The work done to lift an object through a height h above the ground is 980 J. The work done to lift the same object through height of 2h above the ground would be …
- 490 J.
- 980 J.
- 1 960 J.
- 2 940 J. (2)
1.6 Identical steel balls of equal mass are dropped at the same time into test tubes containing motor oils of different viscosities.
Motor oil with LOWEST viscosity is contained in test tube …
- 1.
- 2.
- 3.
- 4. (2)
1.7 A ray of light is reflected by using a plane mirror as shown below. In the diagram angle P is equal to 71°.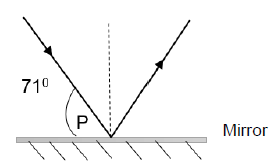
Which ONE of the following is CORRECT regarding the angle of incidence and the angle of reflection?
Angle of incidence | Angle of reflection | |
A | 71° | 71° |
B | 19° | 71° |
C | 19° | 19° |
D | 71° | 19° |
(2)
1.8 Which ONE of the following regarding the dispersion of white light in a glass prism is TRUE?
- Blue light is more refracted than red light.
- Red light is more refracted than blue light.
- Both blue and red light are equally refracted.
- Violet light is refracted less than blue light. (2)
1.9 The magnetic field around a current carrying conductor is shown in the diagram. X indicates that the current flows into the plane of the paper.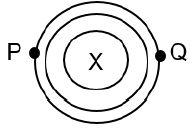
Which ONE of the following is CORRECT regarding the direction of the field and the rule to find the direction of the field?
Direction of the field | Rule to find the direction | |
A | P to Q, clockwise | Right-hand thumb |
B | P to Q, anticlockwise | Left-hand thumb |
C | Q to P, clockwise | Left-hand thumb |
D | Q to P, anticlockwise | Right-hand thumb |
(2)
1.10 Resistors in the circuit diagram given below are identical.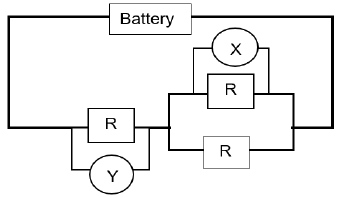
If voltmeter X records a potential difference of V, then the reading on voltmeter Y would be …
- ½V.
- V.
- 2V.
- 4V. (2)
[20]
QUESTION 2: MATCH ITEMS
Choose a term/phrase from COLUMN B that matches a description in COLUMN A. Write only the letter (A–I) next to the question numbers (2.1 to 2.8) in the ANSWER BOOK, for example 2.9 J. Use each term in COLUMN B only ONCE.
COLUMN A | COLUMN B | ||
2.1 | Rate of change of momentum | A | Impulse |
2.2 | Change in momentum | B | Thrust |
2.3 | The internal restoring force per unit area | C | Optic axis |
2.4 | The normal force exerted by a liquid at rest on a given surface in contact with it | D | Capacitor |
2.5 | The central horizontal line that passes through centres of curvature of lens surfaces | E | Tension |
2.6 | A device that converts electrical energy into mechanical energy | F | Net force |
2.7 | The force acting on a string or a rope | G | Stress |
2.8 | A device used for separation of frequencies between the woofer (base) speaker and tweeter (high pitch) speaker/electronic noise filtering | H | Principal axis |
I | Electric motor | ||
(8 x 1) [8]
QUESTION 3
A boy carrying a shotput ball stands on a stationary trolley as shown in the figure below. Assume that the trolley is standing on a frictionless surface.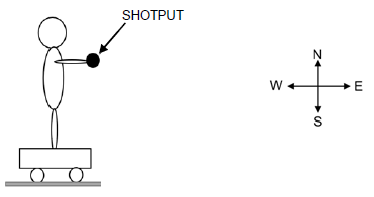
3.1 Write down the ACTION-REACTION pairs for the following forces:
3.1.1 Weight of the boy (1)
3.1.2 Normal force of the ground on trolley (1)
The boy throws the ball in an easterly direction.
3.2 In which direction will the boy-trolley system move after the ball is thrown? (1)
3.3 State the law that explains your answer to QUESTION 3.2 above. (2)
[5]
QUESTION 4
A bricklayer pulls a trolley with a force of 200 N at an angle of 35° to the horizontal on a rough surface as shown in the diagram below.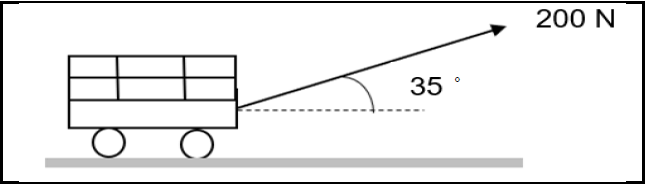
The mass of trolley is 60 kg and the coefficient of kinetic friction between the surface and trolley is 0,2.
4.1 State Newton’s Second law of motion in words. (2)
4.2 Draw a labelled freebody diagram of all the forces acting on the trolley. (4)
4.3 Calculate the magnitude of kinetic friction acting between the surface and the trolley. (4)
4.4 Calculate the magnitude of acceleration of the trolley. (3)
4.5 What would happen to the acceleration calculated in QUESTION 4.4, if the angle between the force applied and horizontal is increased to 50°? Write down only INCREASES, DECREASES or REMAINS THE SAME. Explain your answer. (3)
[16]
QUESTION 5
5.1 A car travels due east with an initial momentum of 20 000 kg.m.s-1 and an initial kinetic energy of 200 000 J.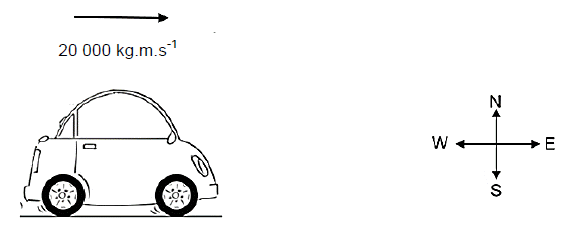
5.1.1 Is momentum a vector quantity? YES or NO. (1)
5.1.2 Calculate the initial velocity of the car. (4)
5.1.3 Calculate the mass of the car. (2)
5.2 Two blocks, P and Q, both at rest have a compressed spring between them. A third block R is in contact with block P as shown below.
After the spring is released blocks P and R moves as a combined unit to the left while block Q moves at a speed of 2 m.s-1 to the right as shown in the diagram below.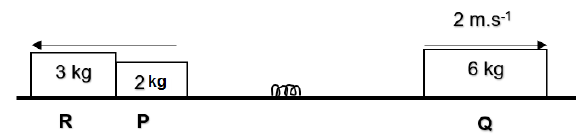
5.2.1 State the law of conservation of momentum. (2)
5.2.2 Calculate the speed of the block P and R combination after the collision. (4)
[13]
QUESTION 6
6.1 A bricklayer pulls a concrete block on a rough surface by applying a constant horizontal force of 300 N.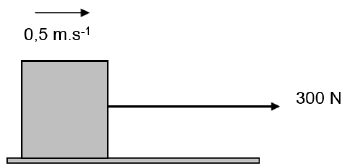
The bricklayer pulls the concrete block for 50 s and it moves with a constant speed of 0,5 m.s-1.
6.1.1 Define the term power. (2)
6.1.2 Calculate the power generated by the bricklayer. (3)
6.1.3 Calculate the work done by the bricklayer. (3)
6.1.4 What is the work done by the force of friction? Give a reason. (2)
6.2 A ball of mass 2 kg is released from point A at the top of curved frictionless track. Point A is at a height of 10 m above the ground. The ball travels to the lowest point B on the track and finally reaches point C.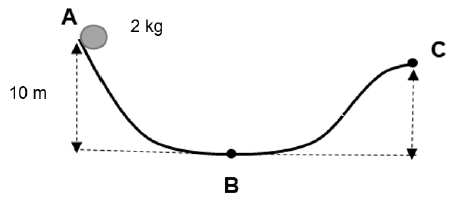
6.2.1 State the law of conservation of mechanical energy in words. (2)
Using energy principles to calculate the:
6.2.2 Speed of the ball at the point B (4)
6.2.3 Height of point C above the ground if the speed of the ball at C is half the speed at B (4)
[20]
QUESTION 7
7.1 One end of a steel rod of length 0,9 m with a cross-sectional area 0,01 m2 is attached to a ceiling. A force 500 N is applied to the other end of the rod as shown in the diagram below.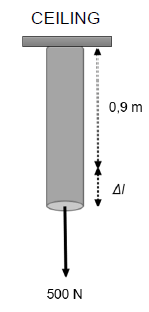
The modulus of elasticity of the steel rod is 200 × 109 Pa.
7.1.1 State Hooke’s law. (2)
7.1.2 Calculate the stress the steel rod experiences. (3)
7.1.3 Calculate the change in length, Δl, of the steel rod after the application of the force. (6)
7.1.4 How does the stress on the steel rod change if a steel rod with higher cross-sectional area is used? Write down only INCREASES, DECREASES or REMAINS THE SAME. (1)
7.2 Viscosity is an important property of a liquid and is temperature dependant. What is the effect of an increase in temperature on viscosity? (2)
7.3 A hydraulic system with pistons A and B is used to lift a vehicle of mass 1 200 kg in an auto garage. A force is applied on piston A while the car sits on piston B of area 0,7 m2. The area of piston A is 0,04 m2.
7.3.1 Calculate the force applied on piston A to lift the car. (4)
7.3.2 Give any TWO uses (other than one which is mentioned above) of hydraulics in technology. (2)
[20]
QUESTION 8
8.1 A coin of diameter 30 mm placed at a distance of 50 cm from a plane mirror as shown in the diagram.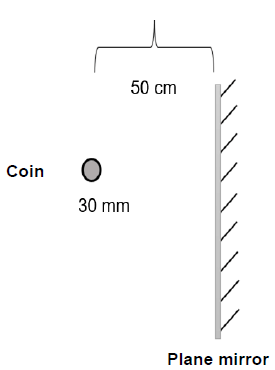
8.1.1 What is the size of the image formed? Write down LARGER THAN OBJECT, SMALLER THAN OBJECT or SAME AS OBJECT. (1)
8.1.2 How far from the object will the image be formed? (2)
8.2 The figure below shows the two rays of light passing from water to air. RAY 1 strikes the boundary between water and air at an angle β and it grazes over the surface of water.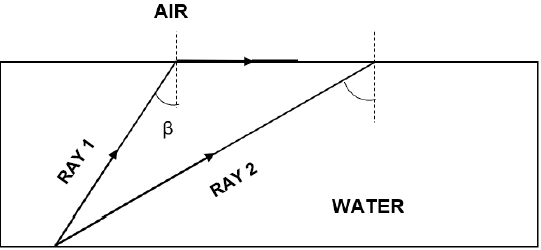
The critical angle for water is 48,8°.
8.2.1 What is the angle of incidence β for RAY 1? (1)
8.2.2 RAY 2 strikes at the boundary at an angle of incidence greater than the critical angle. Explain the path of the ray of light after it strikes the boundary. (2)
8.2.3 Name the phenomenon that takes place in QUESTION 8.2.2. (1)
8.3 An object of height 20 mm placed at a distance 24 cm away from a biconvex lens of focal length 12 cm.
8.3.1 What is the position of the image from the lens? (1)
8.3.2 What is the height of the image? (1)
8.3.3 Is the image formed real or virtual? (1)
8.3.4 Write down ONE use of a convex lens. (1)
[11]
QUESTION 9
9.1 Gamma rays and X-rays are part of an electromagnetic spectrum.
9.1.1 Which RADIATION has photons with the HIGHEST energy? GAMMA RAYS or X-RAYS (1)
9.1.2 Give ONE use of gamma rays. (1)
9.2 An X-ray photon has a wavelength of 1 × 10-10 m.
9.2.1 Define a photon. (2)
9.2.2 Calculate the energy of the X-ray photon. (5)
[9]
QUESTION 10
10.1 A capacitor with a capacitance of 480 × 10-9 F has two parallel plates placed 0,012 mm apart and the space between the plates is filled with air.
10.1.1 Define the term capacitor. (2)
10.1.2 Calculate the area of the plate of the capacitor. (3)
10.1.3 What would happen to the capacitance of the above capacitor if the distance between the plates is increased? Write only INCREASES, DECREASES or REMAINS THE SAME. (1)
10.2 Three resistors of resistances 3 Ω, 6 Ω and 9 Ω are shown in the diagram below. The battery has an emf of 24 V.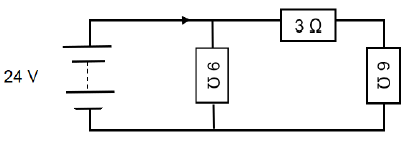
10.2.1 Calculate the total resistance of the circuit. (3)
10.2.2 Calculate the energy developed across 9 Ω resistor in 120 s. (3)
[12]
QUESTION 11
11.1 A learner conducts an experiment to demonstrate electromagnetic induction by pushing a magnet into a coil.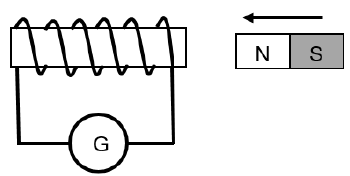
11.1.1 Define electromagnetic induction. (2) What will be observed on the galvanometer (G) needle …
11.1.2 when the magnet is pushed into the coil? (1)
11.1.3 if the magnet is kept stationary inside the coil? Explain your answer. (2)
11.2 The magnetic flux through a coil of wire contains two loops changes from 38 Wb to 50 Wb in 0,42 s. Calculate the emf induced in the coil. (3)
[8]
QUESTION 12
12.1 A transformer in a portable radio reduces 230 V AC to 9 V DC. The primary coil contains 400 turns.
12.1.1 Calculate the number of turns in the secondary coil. (3)
12.1.2 What type of transformer (step up or step down) is this? (1)
12.2 A simplified AC generator is shown in the diagram below.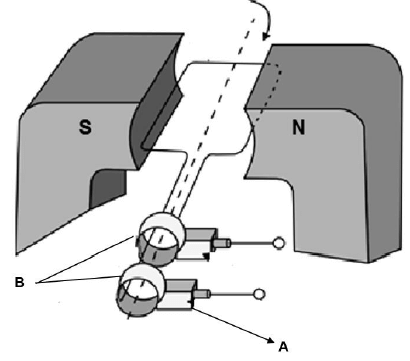
12.2.1 On which principle or law is the working of the generator based? (1)
12.2.2 Name the component labelled A. (1)
12.2.3 Name the component labelled B. (1)
12.2.4 How do you convert an AC generator into a DC generator? (1)
[8]
TOTAL: 150
DATA FOR TECHNICAL SCIENCES
GRADE 12
PAPER 1
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m·s-2 |
Speed of light in a vacuum | c | 3,0 x 108 m·s-1 |
Planck's constant | h | 6,63 x 10-34 J·s |
Permittivity of free space | ɛ0 | 8,85 × 10-12 F.m-1 |
TABLE 2: FORMULAE
FORCE
WORK, ENERGY AND POWER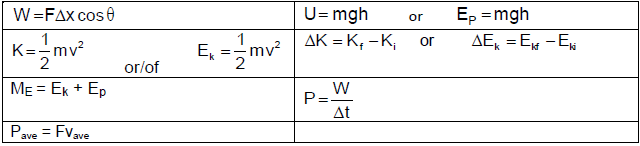
ELASTICITY, VISCOSITY AND HYDRAULICS
WAVES, SOUND AND LIGHT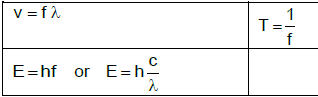
ELECTROSTATICS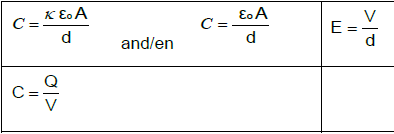
CURRENT ELECTRICITY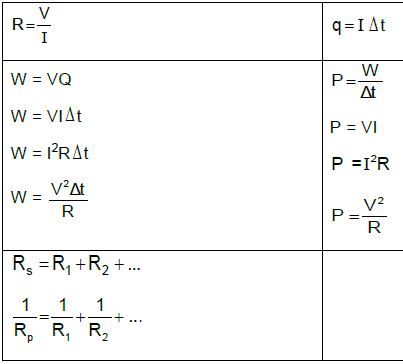
ELECTROMAGNETISM
Technical Mathematics Paper 2 Memorandum - Grade 12 September 2021 Preparatory Exams
NOTE:
- Continuous accuracy (CA) applies only where indicated in this marking
- Assuming values/answers in order to solve a problem is
MARKING CODES | |
M | Method |
A | Accuracy |
AO | Answer only |
CA | Consistent accuracy |
F | Formula |
I | Identity |
R | Rounding |
S | Simplification |
ST | Statement |
RE | Reason |
ST RE | Statement and correct reason |
SF | Substitution correctly in correct formula |
NPU | No penalty for omitting units |
MEMORANDUM
QUESTION 1
Q | M | |
| ||
1.1 | ? = −4 | √ A (1) |
1.2 | ??2 = (−2 + 5)2 + (−4 − 0)2 | √ M |
1.3 | ??? = −4−0 | √ − 4 A 3 √ 53,13° CA √ 126,87° CA (3) |
1.4 | ?? = 3 − (−2) = 3 + 2 = 5 units | √ ?? & ?? M |
[10] |
QUESTION 2
Q | M | ||
2.1.1 | ?2 + ?2 = 25 … 1 | √ ? = ? + 1 | |
2.1.2 | (3; 2): (3)2 + (2)2 = 13 | √ 13 | |
2.1.3 | ???? = 0−3 | √ − 3/4 √ 4/3 √ 25/3 = ? √ ? = 4/3 ? + 25/3 CA (4) | |
2.2 | 36?2 + 49?2 = 1764 |
| √ ?2 + ?2 = 1 |
[18] | |||
QUESTION 3
Q | M | ||||||||
3.1.1 |
| √ SF √ −0,8 | (2) | ||||||
3.1.2 |
| √ 1 √ SF √ −1,4 | (3) | ||||||
3.2.1 | ????̂ = 5 = −5 OR ????̂ = 5 = −5 |
r2 = (-12)2 + (-5)2 | √ ???? = 5 = −5 A √ correct quadrant √ ? = 13 A √ 1 or ?????2?̂ = (13/-5)2 CA √ 169/25 CA (5) | ||||||
3.2.2 | ????̂ − ????̂ = 1 − ????̂ | OR ????̂ − ????̂ = 1 − ????̂ | √ 1 ?? 13 √ 1 √ −109 CA (3) | ||||||
3.2.3 | ????̂ = 5/12 ?̂ = 202,62° | √ method √ 22,62° √ 202,62° | (3) | ||||||
[16] | |||||||||
QUESTION 4
Q | M | |
4.1 | ???(? − ?). ?????(2? − ?). ???(? + ?) | √ correct conversion of rad to degrees √ ???(?) √ − 1 √ ???(?) √ 1 √ ???(?) √ −1.???(?) √ −tan (?) (8) |
OR | ||
???(? − ?). ?????(2? − ?). ???(? + ?) | √ correct conversion of rad to degrees | |
4.2 | ???/?? = ???? − ???? | √ ????
|
[13] | ||
QUESTION 5
Q | M | ||||
5.1 | 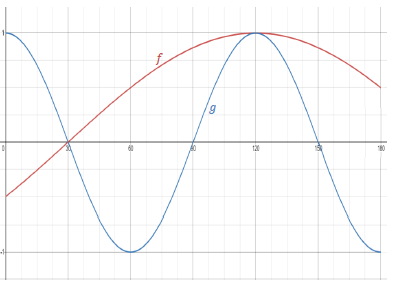 | √ cos start and end point √ cos turningpoints √ cos ?- intercepts √ sin start and end point √ sin turningpoints √ sin ?- intercepts (6) | |||
5.2.1 | 120° | √ 120° | (1) | ||
5.2.2 | (a) | ? = 30° and / en ? = 120° | √ ? = 30° √ ? = 120° | (2) | |
(b) | 90° ≤ ? ≤ 150° | √ 90° ≤ √ ≤ 150° | (2) | ||
[11] | |||||
QUESTION 6
Q | M | |
| ||
6.1 | AB = 8 cm (opp sides of rec = ) | √ 8 cm ST |
6.2 | ?? = tan 30° | √ ?? = tan 30° M |
6.3 | sin ??̂? = sin 30° | √ SF |
6.4 | ??̂? = 180° − 30° − 77° | √ ST RE |
6.5 | ??2 = ??2 + ??2 − 2(??)(??) cos ??̂? | √ (9)2 + (10)2 − 2(9)(10) cos(25°) SF |
[13] |
QUESTION 7
Q | M | ||
7.1 | double the size of the angle subtended by the same arc at the circumference of a circle | (1) | |
7.2 | | ||
7.2.1 | ??̂? = 180° − 48° …(suppl. ∠’s) | √ ST RE | (1) |
7.2.2 | ?̂ = ½ (132°)…( ∠ at centre = 2 x ∠ at circum.) | √ RE √ 66° ST | (2) |
7.2.3 | ??̂? = 90° …( tan ⊥ rad) | √ ST √ RE √ ST RE | (3) |
7.2.4 | ?̂ = ??̂? = 42° …(∠′s opp.= sides) | √ ST RE √ ST RE | (2) |
7.2.5 | ??2 = ??2 − ??2 ….(Pythagoras) | √ M Pythagoras √ ST ??2 = 24 √ ST ?? = √24 | (3) |
[12] | |||
QUESTION 8
Q | M | |
8.1 | supplementary | √ (1) |
8.2 |
| |
8.2.1 (a) | ??̂? = ?̂ = ? (∠′s subt.chord QR ) | √ ST √ RE (2) |
8.2.2 (b) | ??̂? = 180° − (58° + ?) (opp. ∠′s quad.) = 122° − ? | √ ST RE |
8.2.2 | ?̂ + ??̂? + ??̂? = 180° (int. ∠′s ∆) | √ ST RE |
OR | OR | |
?̂ + ?̂ + ?̂ = 180° (int. ∠′s ∆) | √ ST RE | |
[8] |
QUESTION 9
Q | M | |
9.1 |
| √ ST |
9.2 | | |
9.2.1 | In ∆??? and ∆???: | √ ST RE |
9.2.2 | ?? = ?? = ?? (∆???⦀∆???) | √ ?? = ?? = ?? ST |
9.2.3 | ?? = 15 − 6 = 9 | √ ?? = 9 A |
OR | OR | |
??2 = 15 × 9 (from 9.2.2) | √ ??2 = 15 × 9 A | |
9.2.4 | ?? = 12 = 4 | √ 12 SF A |
9.2.5 | ??̂? = 44° + 52° = 96° ≠ 90° | √ ST |
| OR | ||
??̂? = 180° − 44° − 52° = 86° ≠ 90° | √ ST √ ST RE (2) | |
| [16] | ||
QUESTION 10
Q | M | ||
10.1 | | ||
10.1.1 | ?̂ = 30° × ? | √ × ? | |
10.1.2 | ? = ?? | √ F | (3) |
10.1.3 | Area of a sector / ??? ??? ′? ?????? = ?2? | √ F | (3) |
10.1.4 | Area of a sector / ??? ??? ′? ?????? = ?2? | √ SF | (4) |
10.2 | | |
10.2.1 | ? = 2?? | √ F |
10.2.2 | ? = ??? | √ F |
OR | OR | |
? = ?? | √ F | |
10.2.3 | Linear speed of large pulley | √ F |
10.3 | | |
4ℎ2 − 4?ℎ + ?2 = 0 | √ F | |
OR | OR | |
?? = 4 (line from centre perpendicular to chord) | √ ST RE √ ST RE √ ??2 = (5)2 − (4)2 SF √ ?? = 3 cm CA √ ?? = 2 cm CA (5) | |
[26] | ||
QUESTION 11
Q | M | ||
11.1 | 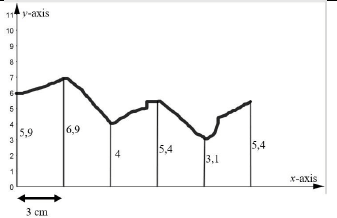 | ||
| √ F OR √ F | ||
11.2 | | ||
| √ F | (3) | |
[7] | |||
TOTAL: | 150 | ||
Technical Mathematics Paper 2 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of ELEVEN questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non- graphical) unless stated otherwise.
- If necessary, round off your answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is attached at the back of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
In the diagram below, A(−5; 0), B(−2; ?), C(3; −4) and D are points on the Cartesian plane. AO ∥ BC and the inclination of DC is ?. BC cuts the ?-axis at E.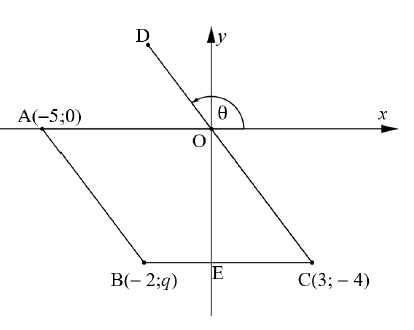
Determine:
1.1 The value of ? (1)
1.2 The length of AB (2)
1.3 The size of ? (3)
1.4 The type of quadrilateral represented by ABCO (4)
[10]
QUESTION 2
2.1 Consider the equations of the circle ?2 + ?2 = 25 and straight line ? − ? − 1 = 0
Determine:
2.1.1 The coordinates of the points of intersection of the line and the circle (7)
2.1.2 Whether the point (3; 2) lies inside, or outside, or on the circle (3)
2.1.3 The equation of the tangent to the circle at point (−4; 3) in the form ? = … (4)
2.2 Plot the graph of the ellipse 36?2 + 49?2 = 1 764 on the grid provided in the SPECIAL ANSWER BOOK. (4)
[18]
QUESTION 3
3.1 If  = 210,5° and B̂ = 122,3°, determine the values of the following correct to ONE decimal place:
3.1.1 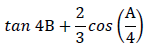 (2)
(2)
3.1.2 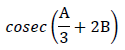 (3)
(3)
3.2 Consider 12???A = 5 and 90° < Â < 360° . Determine the value of the following, without the use of a calculator:
3.2.1 ?????2A (5)
3.2.2 ???A − ?i?A (3)
3.2.3 Determine the size of  , with the use of a calculator. (3)
[16]
QUESTION 4
4.1 Simplify: ?i?(? − ?). ?????(2? − ?). ???(? + ?) (8)
???(2? − ?). ???(2? − ?)
4.2 Prove the identity:
???? − ???? = ???? (5)
1 − ?i??
[13]
QUESTION 5
Given ƒ(?) = sin(? − 30°) and ?(?) = ???3? for ? ∈ [0°; 180°]
5.1 Use the set of axes provided in the SPECIAL ANSWER BOOK to draw sketch graphs of the curves of f and g for ? ∈ [0°; 180°]. Clearly show ALL intercepts with the axes, coordinates of all turning points and end points of both curves. (6)
5.2 Use the graphs drawn in QUESTION 5.1, or otherwise, to determine the following:
5.2.1 The period of g (1)
5.2.2 The value(s) of ? ∈ [0°; 180°] for which:
- ƒ(?) = ?(?) (2)
- ƒ(?). ?(?) ≥ 0 (2)
[11]
QUESTION 6
The diagram below shows a vertical rectangle, ABCD. B, E, F and C are on the same horizontal plane. AB ⊥ BE, DC ⊥ BF, BÊA = 60°, BĈE = 30°, DC = 8 cm and EC = 9 cm. EF = ? and CÊF = ?. B, C and F are collinear.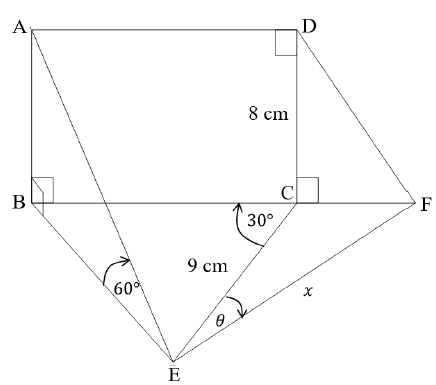
6.1 Write down the length of AB, stating a reason. (2)
6.2 Determine the length of BE, round off to the nearest integer. (2)
6.3 Determine the size of EB̂C, round off to the nearest degree. (3)
6.4 Determine the area of ∆BCE. (3)
6.5 Determine the length of CF, to the nearest integer, if ? = 25° and ? = 10 cm. (3)
[13]
QUESTION 7
7.1 Complete the following statement: “The angle subtended by an arc at the centre of a circle is …” (1)
7.2 The diagram below shows a circle with centre ?. ?, ? and ? are points on the circumference of the circle. OD = OE and BÔE = 48°. DE is a tangent at ?.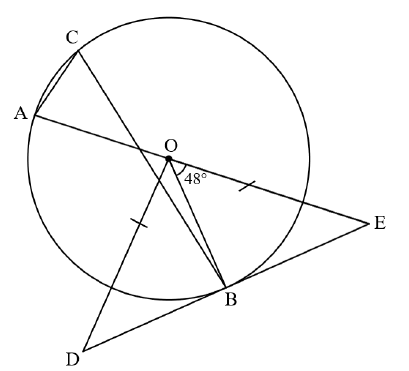
Determine, stating reasons, the size of the following angles:
7.2.1 AÔB (1)
7.2.2 Ĉ (2)
7.2.3 A?̂D (3)
7.2.4 AÔD (2)
7.2.5 If the diameter of the circle is 10 cm and OE = 7 cm, determine the length of BE. (3)
[12]
QUESTION 8
8.1 Complete the following statement: “The opposite angles of a cyclic quadrilateral are …” (1)
8.2 Circle PQRST is drawn below. PŜQ = 58°, ̂P = 72°, Û = 22° and T̂ = ?.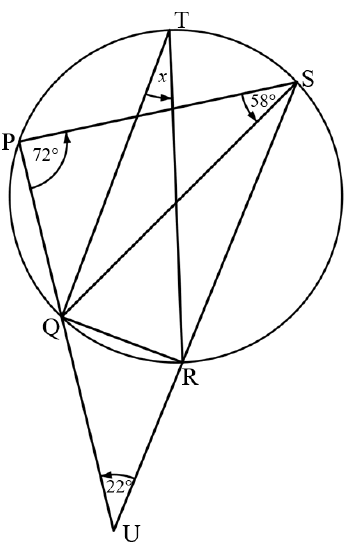
8.2.1 Write down, stating reasons, the size of the following angles in terms of ?:
- QŜR (2)
- PQ̂R (3)
8.2.2 Determine the value of ?. (2)
[8]
QUESTION 9
9.1 Name TWO conditions for triangles to be similar. (2)
9.2 In the diagram below, C, E and D are points on the circumference of a circle. CF is a tangent to the circle at C. FĈD = 52°.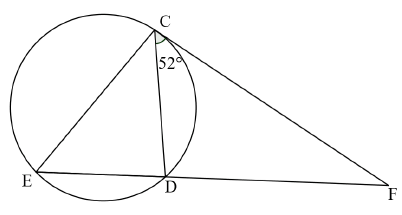
9.2.1 Prove that ∆CDF ∆ECF. (4)
9.2.2 Hence, show that CF2 = EF. FD. (2)
9.2.3 If EF = 15 cm and ED = 6 cm, determine the length of CF to the nearest integer. (4)
9.2.4 Determine CD : EC in simplified form. (2)
9.2.5 Further, if EĈD = 44°, explain whether CE is a diameter of the circle. (2)
[16]
QUESTION 10
10.1 In the diagram below EC and BG are the arc lengths of circle sectors with different radii, that both subtend an angle of 30°. The radii, AG, of the smaller sector is 4 cm and BE is 5 cm.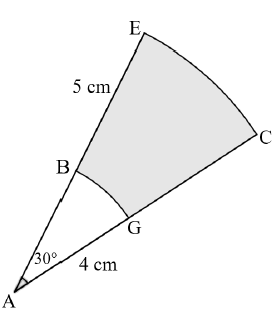
10.1.1 Convert  to radians. (2)
10.1.2 Determine the arc length of BG. (3)
10.1.3 Determine the area of sector AEC. (3)
10.1.4 Hence, determine the area of the shaded area BECG. (4)
10.2 Two pulleys are connected by a belt so that one pulley rotates. The linear speeds of the belt and both pulleys are the same. The radius of the smaller pulley is 3 cm, and the radius of the larger pulley is 15 cm. The smaller pulley is turning at 120 revolutions per minute.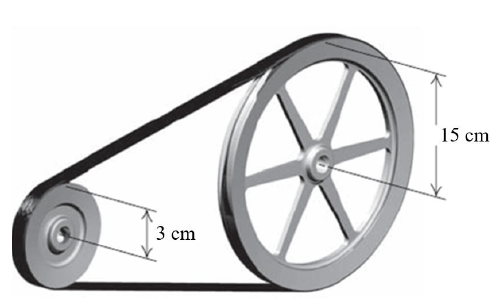
10.2.1 Determine the angular velocity of the smaller pulley. (3)
10.2.2 Hence, determine the linear velocity of the smaller pulley. (3)
10.2.3 Hence, determine the angular velocity of the larger pulley. (3)
10.3 In the diagram below, FG is the diameter of the circle, with a length of 10 cm. CD is a chord of the circle with a length of 8 cm. CD divides the circle into two segments.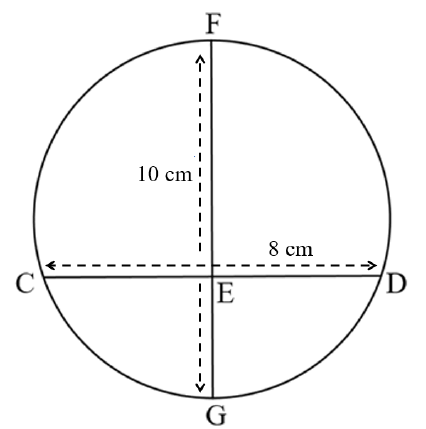
Determine the height of the smaller segment. (5)
[26]
QUESTION 11
11.1 Consider the irregular figure below.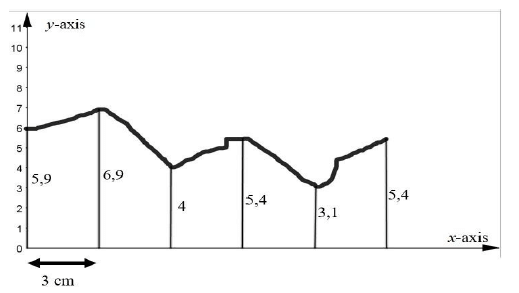
Determine the area of the figure by using the mid-ordinate rule. (4)
11.2 Mr Hlazo wants to collect rainwater from his roof, in a cylindrical tank, to irrigate his garden. The tank needs to be painted. The diameter of the tank is 1,85 ? and the outer height of the tank is 2,5 ?. The tank has an opening at the top with a diameter of 1 ?.
The following formulae may be used:
- Total surface area of a right cylinder = 2??2 + 2??ℎ
- Volume of a right cylinder = (??2) × ℎ?i?ℎ?
Calculate the surface area of the cylindrical tank that will be painted. (3)
[7]
TOTAL: 150
INFORMATION SHEET

Technical Mathematics Paper 1 Memorandum - Grade 12 September 2021 Preparatory Exams
MARKING CODES | |
A | Accuracy |
AO | Answer only |
CA | Consistent accuracy |
M | Method |
R | Rounding |
NPR | No penalty for rounding |
NPU | No penalty for units omitted |
S | Simplification |
SF | Substitution in the correct formula |
NOTE: |
|
MEMORANDUM
QUESTION 1 | ||||
1.1.1 | 21x2 +13x = 0 OR
| ? Factors ? Both x-values OR ? Substitution ? Both x-values | A CA A CA | (2) |
1.1.2 | x + 5 = 7 | ? x2 + 5x = 7 ? Standard form ? Substitution ? Both values of x R | A CA CA CA | (4) |
1.1.3 |
OR | ? Factors M ? Critical Values NPR ? Correct notation OR | A CA CA | |
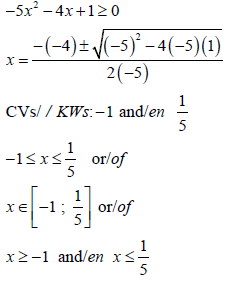 | ? Substitution M ? Critical values NPR ? Correct notation | A CA CA | (3) | |
1.2 | 2x + y = 1............................... (1) | ? Subject of the formula ? Substitution ? Simplification ? Standard form ? Substitution into the formula ? Both x-values ? Both y-values NPR | A CA S CA SF CA CA |
OR
| OR ? Subject of the formule ? Substitution ? Simplification ? Standard form ? SF ? Both y-values ? Both x-values | A CA S CA SF CA CA NPR | (7) | |||||||
1.3.1 | 110 km/h = 110×1000 | AO: 1 Mark | ? 30,55 m/s NPU | A | (1) | |||||
1.3.2 | 30,55 m/s = 3,055 × 10 1 m | ? 3,055 × 10 1 | A | (1) | ||||||
1.4 | 2 | 315 | Remainder | ? Method ? 1001110112 AO: 1 Mark Ignore: No base | A A | (2) | ||||
2 | 157 | 1 | ||||||||
2 | 78 | 1 | ||||||||
2 | 39 | 0 | ||||||||
2 | 18 | 1 | ||||||||
2 | 9 | 1 | ||||||||
2 | 4 | 1 | ||||||||
2 | 2 | 0 | ||||||||
2 | 1 | 0 | ||||||||
1 | 0 | 1 | ||||||||
So 315 = 1001110112 OR 28 + 25 + 24 + 23 + 21 + 20 = 315 | ||||||||||
[20] | ||||||||||
QUESTION 2 | ||||
2.1.1 | It has one root | ? one | A | (1) |
2.1.2 | Real, Rational and Equal | ? Real | A | (3) |
2.2 | (a) P = 1 and b = 3 | ? a = 1 and/en b = 3 | A | (2) |
[6] | ||||
QUESTION 3 | ||||||
3.1 |
| ? Prime factors ? Simplification ? Simplification ? 3
OR ? Simplification ? Simplification ? Simplification ? 3 | A CA CA CA | (4) | ||
3.2 |
| ? Simplification ? Log Property ? Same Base Rule ? Log Property ? Log Property | S CA CA S CA | |||
OR
| OR ? Log Property ? Log Property ? Log Property ? Log Property ? Log Property | S CA CA S CA | (5) | ||
3.3 | 3× 22n+1 - 8n-1 = 4n | ? Common Factor ? Simplification | A CA | (4) | |
3.4.1 | z = 5 – 3i | ? 5 – 3i | A | (1) | |
3.4.2 |
| ?Substitution | A CA | (2) | |
3.4.3 | tanθ = 3 Reference ∠ = 30,96° | ? Tan ratio | A | (4) | |
| 3.5 | (2 - 3i)i + 7 y + 9 = 11+13ix | ? Simplification | S A | (5) | |
| [25] | |||||
QUESTION 4 | ||||||
4.1.1 | 0 = 2x – 1 | ? y = 0 | A CA | (3) | ||
4.1.2 | y = –1 | ? y = –1 | A | (1) | ||
4.1.3 | x = 0 and y = –1 | ? x = 0 | A | (2) | ||
4.1.4 | k(x) = 0 | ? k(x) =0 | A | (2) | ||
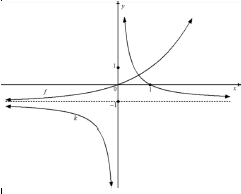
4.1.5 | | ? Common asymptote f: ? Shape ? x-Intercept | CA CA | (5) | ||
4.1.6 | ? ≠ 0 ??, ? ∈ ? ?? − ∞ < | ? | CA | (1) | ||
4.1.7 | f (x) > – 1 | ? Critical value | CA | (2) | ||
4.2.1 | q = – 4 | ? | – 4 | A | (1) |
4.2.2 | 0 = √ 9 - x2 | ? h (x) = 0 | A | (2) | |
4.2.3 | p = -1+ 3 | ? Mid-point | A | (2) | |
4.2.4 | g(x) = a (x – 1)2 – 4 OR g(x) = a (x – 1)2 – 4 | ? Substitute p and q OR ? Substitute p and q | CA | (3) | |
4.2.5 | y = (0 – 1)2 – 4 = – 3 | ? D (3; – 1) | CA | (1) | |
4.2.6 | 0 ≤ x < 3 | ? Critical values | CA | (2) | |
[27] | |||||
QUESTION 5 | |||||
5.1 |
| ? Formula | A | (3) | |
5.2.1 | y = 350 kPa | ? 350 | A | (1) | |
5.2.2 | (c) Compound depreciation | ? Compound depreciation | A | (1) | |
5.2.3 | 27,216 = 350 (1- i)5 | ? Substitution SF | A | (4) | |
5.3 | 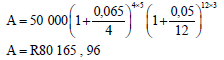
OR
| ? Formula OR ? Formula | A
A | (5) | |
[14] | |||||
QUESTION 6 | ||||
NOTE: PENALISE 1 MARK FOR NOTATION IN QUESTION 6 | ||||
6.1 |
| ? Definition ? Substitution | A CA | (5) |
6.2.1 | x (- 6x + y ) = x3 | ? Divide by x | A | (4) |
6.2.2 |
| ? Exponential form | A | (4) |
| 6.3 | g (-2) = (-2)2 + 3(-2) - 4 | ? g (-2) = -6 | A | (3) |
| [16] | ||||
QUESTION 7 | ||||
7.1 | y = 6 | ? 6 | A | (1) |
7.2 | f (1) = 0 OR f (2) = 0 OR f (3) = 0 | ? f (1) = 0 OR ? f (2) = 0 OR ? f (3) = 0 | A A A | (4) |
7.3 |
| ? f ¢( x) = -3x2 +12x -11 ? f ¢( x) = 0 ? Substitution/Vervanging
? (1,42; − 0;39)
? (2,58 ; 0,39) |
A
A CA
CA CA | (5) |
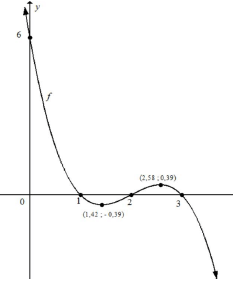
7.4 | | ? Shape | A | (5) |
7.5 | f'( x) = mtangent | ? f '(x) = mtangent | A | (4) |
[19] | ||||
QUESTION 8 | |||||
8.1 | H (0) = 400⸰C | NPU | ? 400 ℃ | A | (1) |
8.2 | H (3) = −2 (3)2 + 20 (3) + 400 | ? Substitution | A | (2) | |
8.3 | dH = - 4t + 20 | ? dH = - 4t + 20 | A | (8) | |
[11] | |||||
QUESTION 9 | |||||
9.1 | 9.1.1 |
| ? 3x5/3 5 ? C | A | (2) |
9.1.2 | 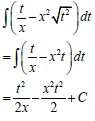 | ? Simplification | S | (3) | |
9.2 |
| ?? Integral form | A | (7) | |
[12] | |||||
TOTAL: | 150 | ||||
Technical Mathematics Paper 1 Questions - Grade 12 September 2021 Preparatory Exams
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of NINE questions.
- Answer ALL the questions.
- Answer QUESTION 4.1.5 and QUESTION 7.4 on the ANSWER SHEETS provided. Write your name and school name in the spaces provided on the ANSWER SHEETS and hand in the ANSWER SHEETS with your ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise. If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is attached at the back of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 21x2 +13x = 0 (2)
1.1.2 x + 5 = 7 (correct to TWO decimal places) (4)
x
1.1.3 –5x2 – 4x + 1 ≥ 0 (3)
1.2 Solve the following systems of equations simultaneously: 2x+ y = 1 and x2 + y2 + 2x - 6y = 9 (7)
1.3 The speedometer below shows the speed of a car travelling at 110 km/h.
1.3.1 Express 110 km/h in m/s, if 1m = 1 000 km. (1)
1.3.2 Write the solution in QUESTION 1.3.1 above, in Scientific Notation. (1)
1.4 Convert 315 to binary notation, WITHOUT using a calculator. (2)
[20]
QUESTION 2
2.1 Given: (x - √23)(x - √23) = 0
2.1.1 Write down the number of root(s) the above equation has. (1)
2.1.2 Hence, or otherwise, describe the nature of the root(s). (3)
2.2 The sketch below represents the graph of a function f defined by f (x) = ax2 + bx+3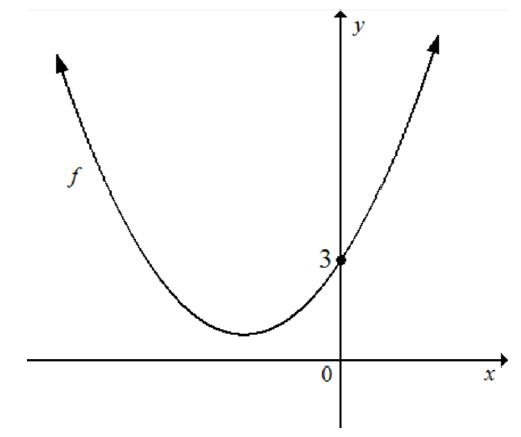
Use the graph above to answer the following questions.
Given:
| OPTION | Value of a | Value of b |
| P | 1 | 3 |
| Q | ½ | 3 |
| R | -1 | 3 |
| S | 1 | -3 |
Using the information given in the table above, choose any option(s) that will satisfy the condition that the roots of f are imaginary. (2)
[6]
QUESTION 3
3.1 Simplify without using a calculator.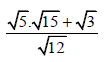 (4)
(4)
3.2 Show (without using a calculator) that: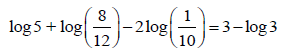 (5)
(5)
3.3 Solve for n:
3.22n +1 – 8n – 1 = 4n (4)
3.4 The accompanying graph shows an Argand diagram of a complex number, z, with point P (5 ; – 3):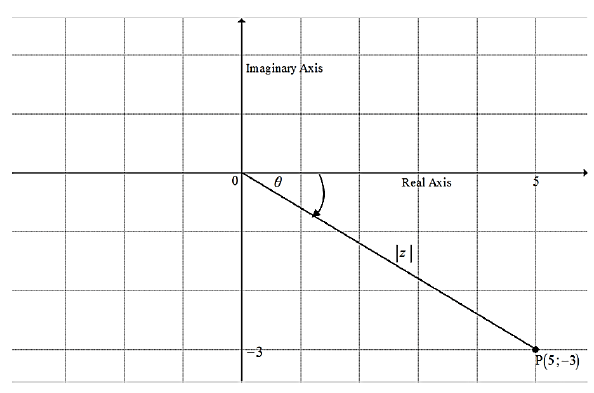
3.4.1 Write down the complex number in rectangular form, z = a + bi (1)
3.4.2 Calculate the modulus of z. (2)
3.4.3 Express the complex number as z = r cisθ (4)
3.5 Solve for x and y if: (2 - 3i)i + 7y + 9 =11 + 13ix (5)
[25]
QUESTION 4
4.1 Given the functions f (x) = 2x -1 and k (x) = 1 - 1
x
4.1.1 Determine the coordinates of the x-intercept of f . (3)
4.1.2 Write down the equation of an asymptote of f. (1)
4.1.3 Write down the equations of asymptotes of k. (2)
4.1.4 Determine the x-intercept of k. (2)
4.1.5 Sketch the graphs of f and k on the ANSWER SHEET provided, indicating the asymptote(s) and intercept(s) of the graphs. (5)
4.1.6 Write down the domain of k. (1)
4.1.7 Write down the range of f. (2)
4.2 Sketched below are the graphs of g (x) = a( x - p)2 + q and h( x) = √9 - x2 .
- Points A, B and C are the intercepts of h.
- x = – 1 and point C are the x-intercepts of the graph of g.
- Point D is the y-intercept of g.
- E(p ; – 4) is the turning point of g.
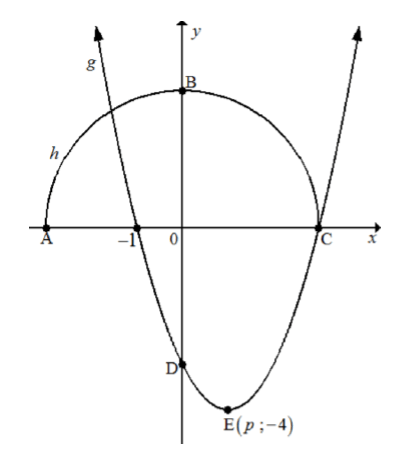
4.2.1 Write down the numerical value of q. (1)
4.2.2 Determine the coordinates of C. (2)
4.2.3 Calculate the numerical value of p, the x-coordinate of point E. (2)
4.2.4 Determine the numerical value of a. (3)
4.2.5 Hence, or otherwise, determine the coordinates of D. (1)
4.2.6 Determine the values of x ≥ 0 for which h (x) > g (x). (2)
[27]
QUESTION 5
5.1 Determine the effective interest rate of 4,5% nominal interest rate per annum, compounded monthly. (3)
5.2 The table below shows pressure readings over time taken on a car tyre using a pressure gauge, as shown in FIGURE 1. The pressure readings are taken over a period of 5 minutes. Pressure is measured in kilo Pascals (kPa).
The graph, with A as the y-intercept, alongside in FIGURE 2, represents the points recorded in the table below.
TIME (Minutes) | PRESSURE (kPa) |
0 | 350 |
1 | 210 |
2 | 126 |
3 | 75,6 |
4 | 45,36 |
5 | 27,216 |
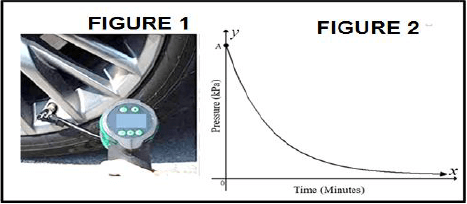
5.2.1 Write down the y-coordinate of point A as shown in the graph. (1)
5.2.2 Which rate best describes the change in pressure over 5 minutes?
Hint: Refer to the table or FIGURE 2. (1)
- Compound increase
- Simple interest
- Compound depreciation
- Straight Line Depreciation
5.2.3 Hence, or otherwise, determine the rate at which the tyre pressure changes over 5 minutes. (4)
5.3 An amount of R50 000 is invested at an interest rate of 6,5% per annum, compounded quarterly for the first 5 years of the investment. The interest rate then changes to 5% per annum, compounded monthly for the remaining 3 years of the investment. Determine the amount of money accumulated by the investment at the end of the 8-year investment period. (5)
[14]
QUESTION 6
6.1 Determine the derivative of f (x) = 13ax - 2b by using FIRST PRINCIPLES. (5)
6.2 Determine:
6.2.1 dy if x(-6x + y) = x3 (4)
dx
6.2.2 ![]() (4)
(4)
6.3 Determine the average gradient of g (x) = x2 + 3x – 4 between x = – 2 and x = 1. (3)
[16]
QUESTION 7
Given: f (x) = – x3 + 6x2 – 11x + 6
7.1 Write down the y-intercept of f. (1)
7.2 Determine the x-intercepts of f. (4)
7.3 Determine the coordinates of the turning points of f. (5)
7.4 Sketch the graph of f on the ANSWER SHEET provided, showing all the intercepts and the turning points of f. (5)
7.5 Determine the possible value(s) of x for which h(x) = –11x + q is a tangent to f . (4)
[19]
QUESTION 8
The diagram below shows, a quick industrial reaction between hydrogen gas and nitrogen gas, in the presence of a catalyst, to produce liquid ammonia known as the Haber process. The amount of ammonia produced is proportional to the temperature at that particular time. The heat of reaction is a function of time, ?(?) = −2?2 + 20? + 400; ? ≥ 0 measured in ºC and time (t) in seconds.
Determine:
8.1 The heat at the start of the reaction (1)
8.2 The heat (H) after 3 seconds (2)
8.3 The time taken to change from freezing temperature to maximum temperature (8)
[11]
QUESTION 9
9.1 Determine the following integrals:
9.1.1 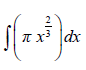 (2)
(2)
9.1.2 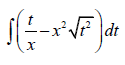 (3)
(3)
9.2 The sketch below shows the shaded area bounded by the curve of the function defined by f (x) = x3 – x and the x-axis between points x = – 1 and x = 1.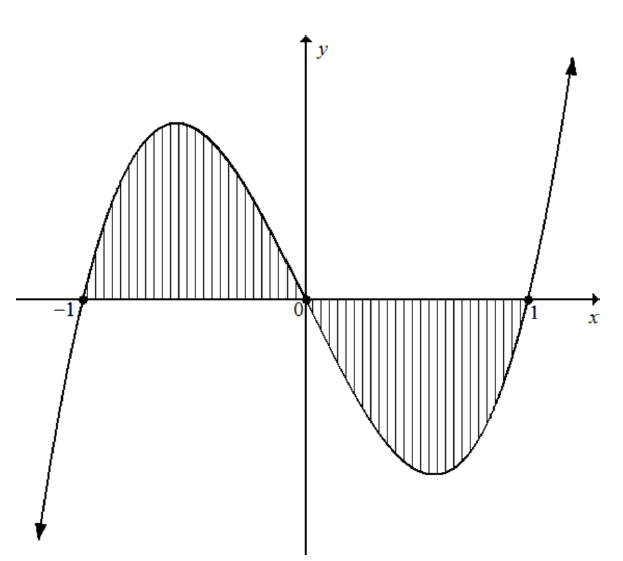
Determine (showing ALL calculations) the shaded area bounded by the curve f and the x-axis between the points where x = − 1 and x = 1. (7)
[12]
TOTAL: 150
INFORMATION SHEET: TECHNICAL MATHEMATICS

ANSWER SHEET
SURNAME: ………………………………….. NAME: ……………………………………….
SCHOOL: ………………………………………. CLASS: ………………………………………
QUESTION 4.1.5
ANSWER SHEET
SURNAME: …………………………………….. NAME: ……………………………………….
SCHOOL: ………………………………………. CLASS: ………………………………………
QUESTION 7.4
Religion Studies Paper 2 Memorandum - Grade 12 September 2021 Preparatory Exams
MEMORANDUM
QUESTION 1
1.1
1.1.1 The nature of humanity, with reference to community and individual
- Christians believe that humans were created in the image of God.
- After creating Adam and Eve, God instructed them to look after the Garden of Eden and whole of creation.
- As co-creator with God, humans are God’s representatives on earth.
- God has appointed them to look after His property, the world.
- Christians believe that human beings were created to be immortal.
- However Adam and Eve disobeyed God’s commandments.
- The penalty for this sin was death for the human race.
- Even after this condemnation, God still tried to liberate humanity from evil and death.
- After death, Christians envisage a new community that will be marked by love. (10)
1.1.2 Nature of life after death
- Christians believe that human beings were created to be immortal.
- Adam and Eve disobeyed Gods commandments.
- The penalty for this sin was death for the human race.
- After this condemnation, God still tried to liberate humanity from evil and death.
- After death, Christians envisage a new community that will be marked by love, sharing and caring.(10)
1.1.3 Nature of divinity
- God is the creator of the universe.
- God is omnipotent which means that He is powerful.
- God is a spirit being.
- God is caring and loving.
(Any other relevant responses must be credited.) (10)
1.2 Internal difference in any ONE religion
1.2.1 Difference in teachings
Teachings in Islam
- Islam is divided into two major groups, namely the Sunni and Shi’a.
Sunni Muslim
- Sunni refers to following the Sunnah (example) of the Prophet Muhammad.
- The Hadith narrated by the companions of the Prophet have equal status to those narrated by his family members.
- The sect believes that all the teachings contained in the Books of Hadith are equally important.
- Sunnis follow the teachings of scholars from the 7th and 8th centuries.
- Sunni do not accept that a caliph can come exclusively from the Prophet’s family.
Shi’a Muslim
- Shia means partisan or separate party.
- The hadith narrated by the companions of the Prophet have less significance than that narrated by his family members.
- The Shi’a follow the teachings and opinions only of a living scholar.(10)
1.2.2 Difference in governance
Sunni
- There is no clergy in Sunni Islam.
- Any Moslem can serve on community boards.
- Governance is community-based.
- Scholars of Islam and community members serve on governing boards of mosques and madrassah and schools.
Shi’a
- Shi’a Muslim revere the descendants of the Prophet Muhammad and that they have the right to lead Muslims.
- They reserve the title ‘Imran’ for certain past leaders who are believed to have been chosen by God.
- The final word in any uncertainty about any religious or political issues lies with the representatives of the Imam.
- Governance is in the hands of mullahs (priests) who rule by religious decree.
(Any other relevant responses must be credited.) (10)
[50]
QUESTION 2
2.1 (For the purpose of this marking guideline Christianity is discussed as an example.)
2.1.1 Causes
- Breaking up of families
- High volume of illegal firearms circulating in society
- Erosion of the moral fibre
- Patriarchy / male dominance
- Poverty
- Adultery
- Alcohol and / or drug abuse
(Any relevant answer should be credited.)(6)
2.1.2 Effects
- Family breakdown
- Justification of violent crimes
- Physical injury and death
- Unstable marriages
- Trauma among the victims
- Increased in child-headed families
- Abuse childhood perpetuating GBV
- Emotional damage in victims and survivors
- Neglected children
- Mental illness like depression
- Femicide
(NOTE: Other responses must be credited.)(10)
2.1.3 Religious teachings
- Violence is prohibited, especially against the weak and vulnerable.
- Good family values are emphasised.
- Fathers are encouraged to love their wives.
- Boys and girls are treated equally.
- Love and peace form part of central teachings.
- Adultery is prohibited.
(NOTE: Other responses must be credited.)(10)
2.2
2.2.1 The World Council of Churches
- Most religious leaders on both sides of the dispute facilitate peace at local levels.
- Even today, people of different religions live peacefully even in one family and across levels. Part of the conflict.
- Religious organisations are still carrying out humanitarian activities to all people affected by the war, irrespective of religion.
- The religious bodies failed to bring political stability at a national level because they have no political power.
- Religious extremism combined with tribal tensions in South Sudan are still part of the conflict.
(Any other relevant responses must be credited.)(8)
2.1.2 Interfaith Action for Peace in Africa (IFAPA)
- Tried to bring together religious communities, civil society, the private sector and government to resolve the conflict.
- The IFAPA was able to work with humanitarian organisations to provide health services, shelters and other basic needs.
- Send interfaith delegations to conflict risk areas.
- Organising exchange visits between landmine victims and survivors from Ethiopia, South Sudan and Uganda.
- The conflict is more political than religious and needs government intervention.
- Even the UN Multidimensional Integrated Stabilisation Mission has not been able to stop abuse in the country. The country is still dominated by a culture of impunity that allows atrocities to prevail.
(Any other relevant responses must be credited.)(6)
2.3 Hermeneutical principles
- Grammar and historical context: This means one must use the rules of grammar and the historical facts to interpret the literal meaning of a text.
- Plan, purpose and context: A piece of writing should be viewed as a whole. What is the writing plan or structure? What was the author's purpose in writing the text? What is the context of the passage being looked at?
- Meaning of words: The meaning of words change over time and in different places. Find out the original meaning as they were used in the normative source.
- Figurative meaning: Figurative and non-literal meaning must be taken into account.
- Other sacred texts: Sacred texts may be used to interpret other sacred texts.
(Any other relevant responses must be credited. Four marks are allocated for mentioning only principles without giving explanation.)(10)
[50]
QUESTION 3
3.1
3.1.1 Materialism
- This worldview originated in various areas within Europe and Asia.
- It originated during the Axial era from 800–200 BCE.
- Materialism expresses itself in ancient Indian philosophy, in Buddhism and Confucianism.
- In the West materialism was first developed by Greek philosophers – the Atomists, and was revived in the 18th century.
- An elaboration of the concepts of materialism was made by Karl Marx during the 19th century.
- Marx included human history and economic activity into materialism.
- It was at this time that the Protestant movement was gaining ground in Europe.
- This emboldened secularists, including materialists, to develop worldviews other than religion.
(Any other relevant responses must be credited.)(10)
Secular humanism
- It was first used as a concept in the 1950s.
- Secular humanism is a branch of humanism.
- The term ‘humanism’ was originally a religious term.
- In the Renaissance era a humanist was anyone who studied classical literature and education.
- This movement initially encouraged people to use their intellect to understand scripture.
- Later it became secular, non religious and atheistic.
- It teaches that supernatural beings are not a necessity for teaching right from wrong.
- Humans can work this out for themselves, using their reasoning skills.
- It rejects religious beliefs and the existence of the supernatural.
(Any other relevant responses must be credited.)(10)
3.1.2 Secularism as a worldview
- Secularism is a belief that government and morality should not be based on religion.
- It does not reject religion, but does not give religion the final say on morality or government.
- Instead, secularism sees human intellect as a solution to all challenges.
- Secularism advocates ethics based on reasoning about human nature, without refering to God or gods.
- Secularism advocates freedom of speech and freedom of religion.
- Secularism understands the universe without appealing to religious explanations, such as Creationism and myths.
(Any other relevant responses must be credited.)(10)
3.2
3.2.1 Oral tradition
- Original inspiration is usually first spread through oral tradition in many religions.
- Oral tradition has been used to transfer religious messages before the religious writings.
- Before the invention of writing, religious traditions were transmitted by word of mouth.
- It is true that these traditions developed, changed and are adapted over time.
- All religion followed oral tradition over many centuries and some still have elements of oral traditions.
(Any other relevant responses must be credited.)(10)
3.2.2 Inspiration
- Inspiration is an important normative source in many religions.
- It is the true origin of all religions.
- Inspiration refers to the power or force of an extraordinary being, 'taking over' a chosen being.
- The founding figures of many religions were inspired by a higher power or wisdom.
- Such people felt that they received 'revelation' from an extraordinary being.
- Examples are Moses, Jesus Christ, Abraham, Prophet Muhammad, Buddha and Baha'u'llah.
- In ATR, mediums or diviners receive inspiration while they are in a trance.
- This inspiration is on-going, while that of the Abrahamic faiths did not go beyond their founders.
- Inspiration is a powerful motivation for the followers of a religion.
(Any other relevant responses must be credited.)(10)
[50]
QUESTION 4
4.1
4.1.1 Darwin’s Theory
- The scientific answer to the question comes from Darwin’s Theory of evolution.
- It state that all forms of life are connected from Darwin’s common origin.
- Organisms change gradually to adapt to changing environments.
- Those that suit the environment best, become dominant.
- This is called “natural selection”.
- The process started many millions of years ago, and is still continuing.
- Human beings also emerged over a long process, spanning millions of years, until ‘modern’ humans finally emerged about 100 000 years ago.
- The theory of evolution asserts that humans evolved from a common primate ancestor that is apes.
(Any other relevant responses must be credited.)(14)
4.1.2
- Christianity
- The Creator is male.
- At first, only the creator existed.
- The Creator made the universe from nothing.
- The process of creation took six days.
- Humans were made on the sixth day.
- There is one perfect God.
- He created the heaven and earth, and all that in it.
- The first two humans were Adam and Eve. God made from clay.
- God breathed His spirit into Adam, and he came to life.
- These humans lived in the perfect Garden of Eden.(12)
- Hinduism
- Hinduism has no problem with evolution. They have more advanced theories which incorporates spiritual evolution.
- The evolution theory did not create conflict with Hindu thought and beliefs. It contributed to the understanding of evolution towards Moksha.
- Therefore, in these religions (Hinduism and Buddhism), there is no change in attitude.
- In African Traditional Religion, there has been no objection to the evolution theory, as the universe is seen as interconnected parts.
- However, the status of man is clearly seen as above all other creation.
(Any other relevant responses must be credited.)(12)
4.1.3 Big Bang Theory
- The Scientific explanation Creation is called the Big Bang Theory.
- According to the Big Bang Theory, it is not known what existed before the Big Bang.
- The Big Bang Theory states that there was enormous explosion and within a second the universe appeared and filled out to an enormous size.
- The Big Bang Theory states that the process of creation occurred within a second.
- According to the scientific account the Big Bang took place 13,7 billion years ago.
- Small temperature differences led to varying densities of matter throughout the universe.
- Those densities formed into clusters of matter and energy.
- The clusters continued to condense in a lump way and eventually formed the vast collection of stars called galaxies.
- Some galaxies condensed into a combination of stars called solar system.
- Scientists believes that the universe is expanding at this moment.
- The scientific account does not mention any Creator.(12)
[50]
TOTAL: 150




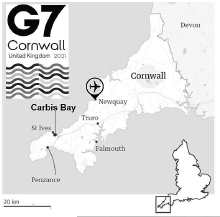

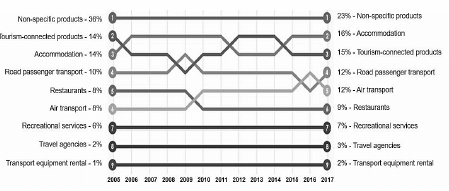
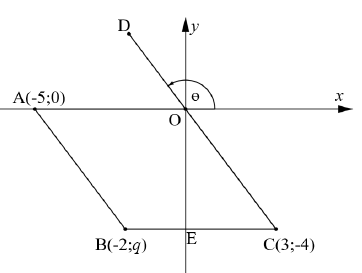
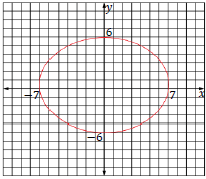
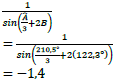
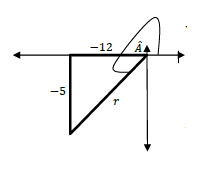
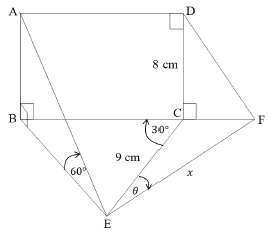
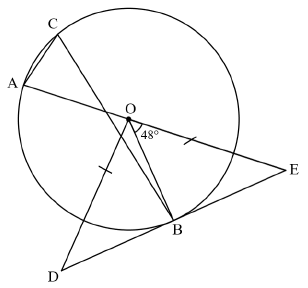
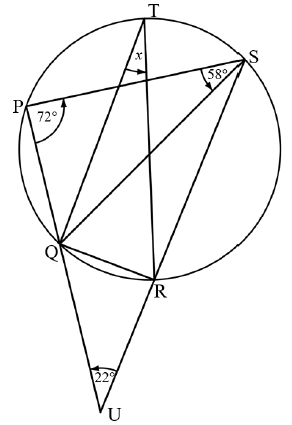
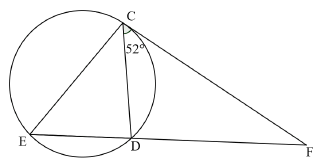
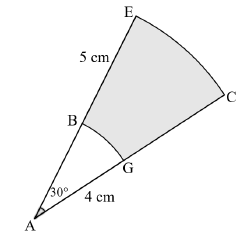
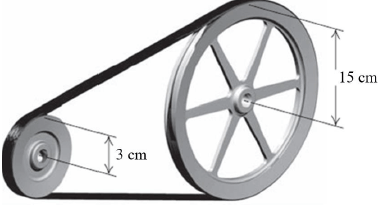
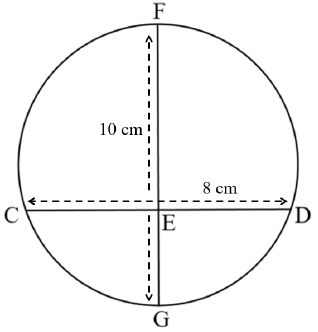
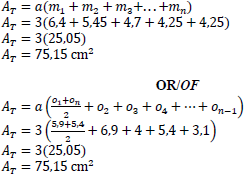
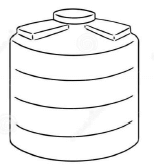
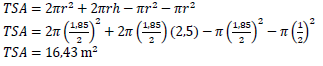
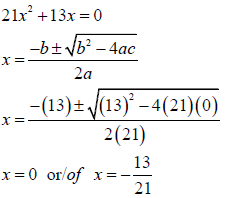
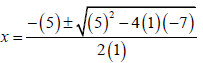
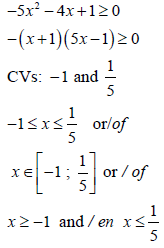
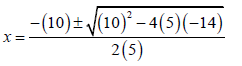
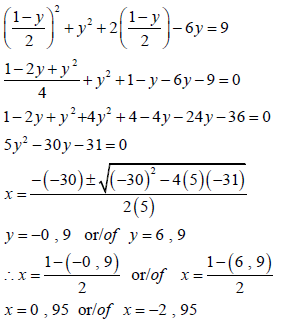
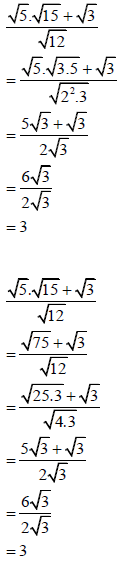 OR
OR