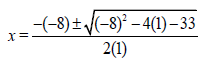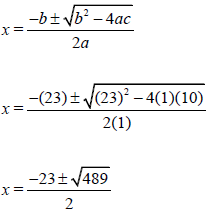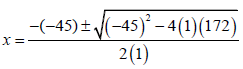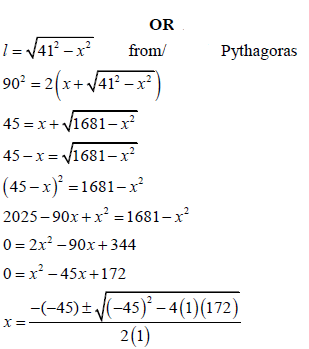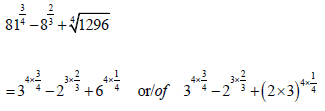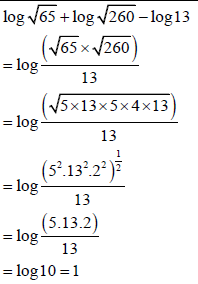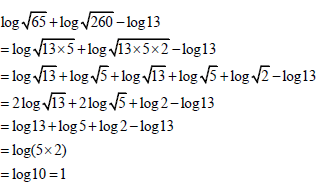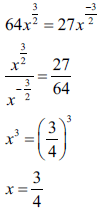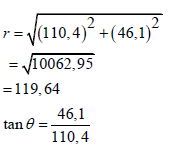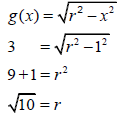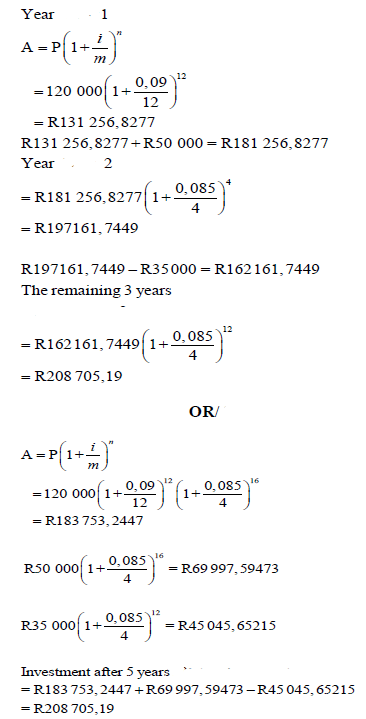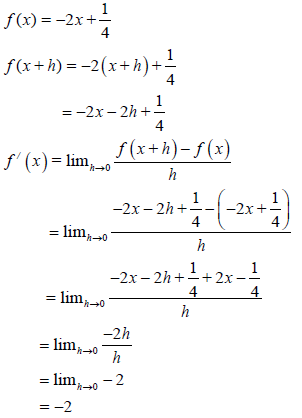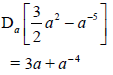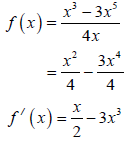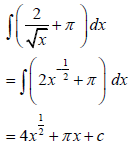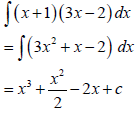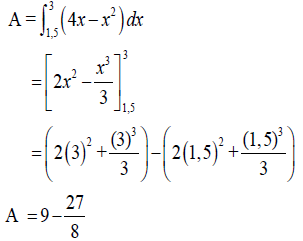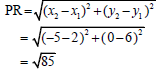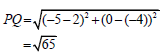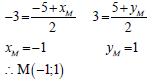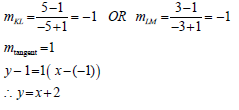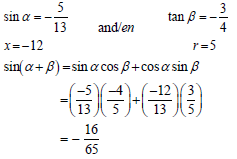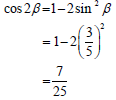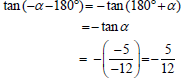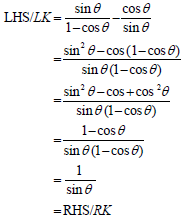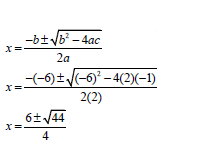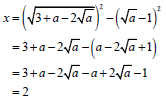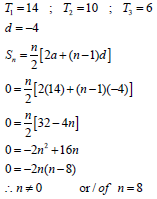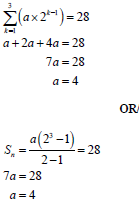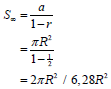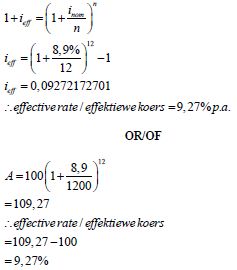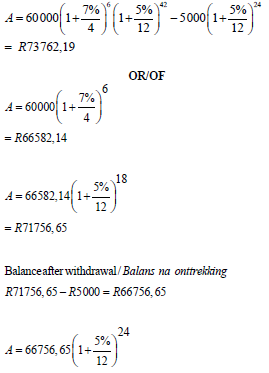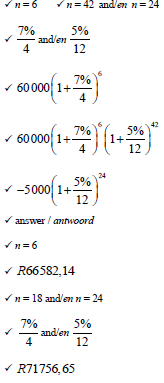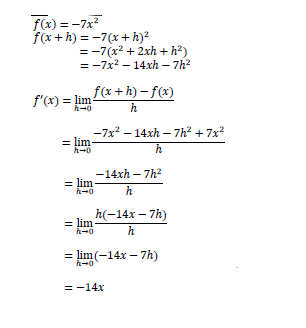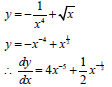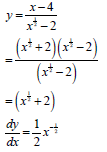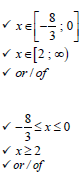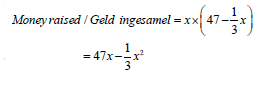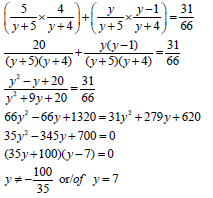Adele
Technical Mathematics Paper 2 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of TEN questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non- graphical) unless stated otherwise.
- If necessary, round off your answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Number the answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The picture below shows the inter passes amongst four soccer players in a premier league match.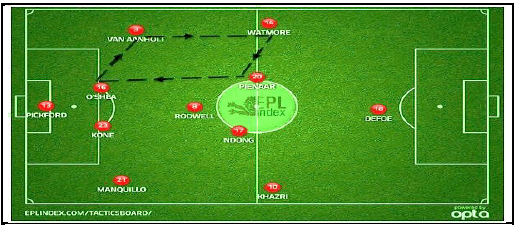
The diagram below, NOT drawn to scale, models the above situation in a Cartesian plane. The diagram below is a parallelogram with vertices A(–2 ; 2) ; B(–4 ; –1) ; C(2 ; 0) and D(4 ; 3); ? is the angle which AB forms with the x-axis.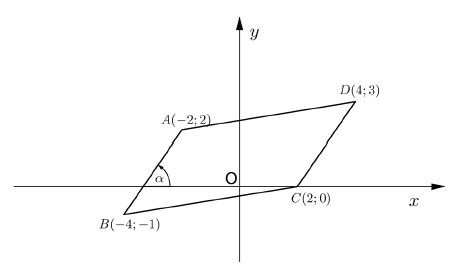
Determine:
1.1 The length of CD (Leave your answer in simplified surd form.) (2)
1.2 The equation of straight line CD in the form ? = ?? + ? (4)
1.3 The gradient of AB (1)
1.4 The size of ? (rounded off to TWO decimal places) (2)
1.5 The coordinates of M, the point of intersection of the diagonals of ABCD (2)
1.6 The equation of the straight line that is perpendicular to CD and goes through the point M. (3)
[14]
QUESTION 2
2.1 The photo below is the aerial view of a certain town. On a certain day, the community held a big function in the town hall. The noise made could be heard in a
radius of 2√2 km from the hall, centre O.
2.1.1 Calculate the equation of the circle from which the noise could be heard. (2)
2.1.2 If a car travels along the road PQ with the equation, x + y = 4 , determine the coordinates of point Q, where the passengers will be able to hear the noise from. (5)
2.1.3 After passing point Q, will the passengers be able to hear the noise? Justify your answer. (2)
2.2 The diagram below gives a schematic presentation of a cycling track. The shape of the track is given by the ellipse equation ![]() . The ellipse intersects the y-axis at B and D. N (ē; -4,8) is a point on the ellipse.
. The ellipse intersects the y-axis at B and D. N (ē; -4,8) is a point on the ellipse.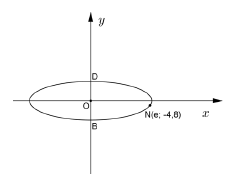
2.2.1 Write down the co-ordinates of B. (2)
2.2.2 Determine the value of e. (3)
[14]
QUESTION 3
3.1 Given: tan β = 2 ; where 90º< β < 270º.
Calculate the following with the aid of a sketch and without the use of a calculator:
3.1.1 sin β (3)
3.1.2 cot (360º - β) + 1 (2)
3.2 If θ = 72º and α = 96º, determine the following, rounded off to TWO decimal digits:
3.2.1 sin (θ + α) (2)
3.2.2 sec α + sin 5π/6 (3)
3.3 If sin 24º = m , determine cos156º in terms of m. (3)
[13]
QUESTION 4
4.1 Complete the following identity: ?????2(10?) − ???2(10?) = ... (1)
4.2 Simplify the following to a single trigonometric ratio:
tan (180º - x)sin (180º + x)cos x (7)
sec2 x
4.3 Prove the following identity using fundamental identities and without using a sketch:
cot2 x sin2 x + sin x = 1 (3)
cosec x
4.4 Solve for ? ∈ [0°; 360°], rounded off to ONE decimal digit:
4.4.1 sec 2x = 2 (4)
4.4.2 2 tan (x - 30°) = -3 (5)
[20]
QUESTION 5
The diagram shows the graph of f(x) = cos 2x for x ∈[0°;360°].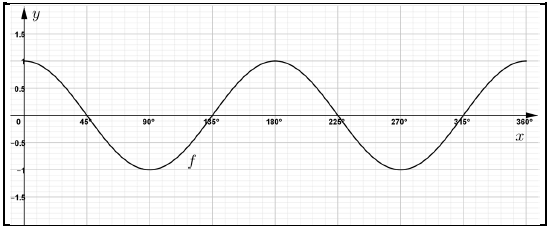
5.1 Draw, on the same set of axes in the SPECIAL ANSWER BOOK, the graph of
g(x) = sin (x - 45°) for x ∈[0°;360°].
Clearly indicate ALL the turning points, starting and end points and intercepts with the axes. (3)
5.2 Use the graphs to determine the following:
5.2.1 The amplitude of g (1)
5.2.2 The period of f (1)
5.2.3 The range of g (2)
5.2.4 f (135°) - g (135°) (2)
5.2.5 The values of x for which f(x) = 1 for x ∈[0°;360°] (3)
5.2.6 The values of x for which f(x) < 0 for x ∈[180°;360°] (2)
5.2.7 The values of x for which f (x)g(x) ≥ 0 for x ∈[0°;360°] (2)
5.2.8 For which value(s) of x is f ́ (x) ˃ 0 for x ∈[0°;180°] (2)
[18]
QUESTION 6
6.1 Complete the following statement:
In any ∆PQR, sin P = sin Q (1)
p ...
6.2 In the diagram below, ∆ABC is drawn with D on AB. Further, BÂC = 80°, BC = 11 units, BD = 6 units and AD = 4 units.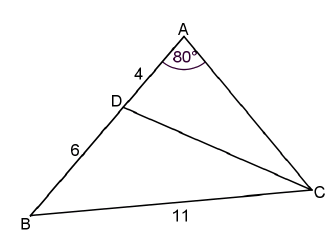
6.2.1 Calculate, rounded off to the nearest degree, the size of ABC. (4)
6.2.2 Hence or otherwise, determine the length of DC. (4)
6.2.3 Determine the area of ∆DBC. (3)
6.2.4 Determine the length of AC. (3)
[15]
QUESTION 7
7.1 Complete the following theorem:
A line drawn from the centre of a circle perpendicular to a chord … (1)
7.2 Given a circle with centre O with OR ⊥ PT, radius OB = 8 cm and PR = 2 cm.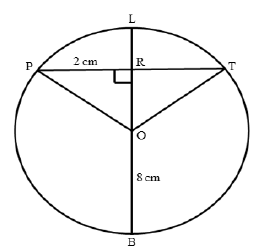
7.2.1 Determine, stating a reason, the length of PT. (3)
7.2.2 Calculate the length of LR. (4)
[8]
QUESTION 8
8.1 Complete the following theorem: Two tangents drawn to a circle from the ... outside the circle are equal in length. (1)
8.2 In the diagram below CD and DE are tangents at C and E respectively to the circle.
C, F and E lie on the circumference of the circle.
DG is parallel to FE with G on FC.
CDE = 46º and CGD = x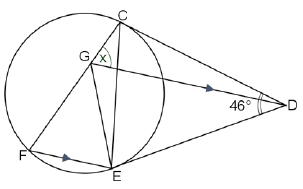
8.2.1 Determine, stating reasons, the value of x. (6)
8.2.2 Hence or otherwise show that C, G and D lie on the circumference of a circle. (2)
8.2.3 If CGED is a cyclic quadrilateral, determine, stating reasons, the size of GEF . (3)
8.2.4 Calculate the size of FGˆ E by providing at least two methods of calculating the angle. (3)
8.3 In the diagram below, BE is the diameter of the circle ABCE with centre O.
GF is a tangent to the circle at point C.
EBC = 25º and ABE = 48º .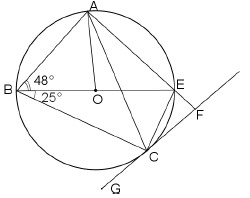
Determine, giving reasons, the size of the following angles:
8.3.1 BÂE (2)
8.3.2 AÔE (2)
8.3.3 CÊF (2)
8.3.4 EĈF (2)
8.3.5 AĈE (2)
8.3.6 AĈG (3)
[28]
QUESTION 9
9.1 Complete the following theorem: A line drawn parallel to one side of a triangle divides the other two sides … (1)
9.2 In ΔABC below, BCisproduced to G. ![]()
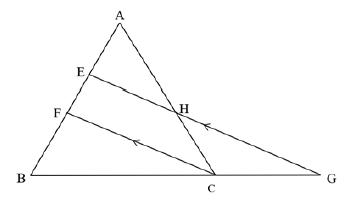
9.2.1 Complete, with reason: AE = ... (2)
EF
9.2.2 Determine the length of EF. (3)
9.2.3 If EF = 5 , determine FB. (1)
2
9.2.4 Hence, or otherwise show that BG cannot be more than 3 units. (3)
GC
[10]
QUESTION 10
In the diagram below, BCDE is a circle. Chords CB and DE are produced to meet in A.
AE = DC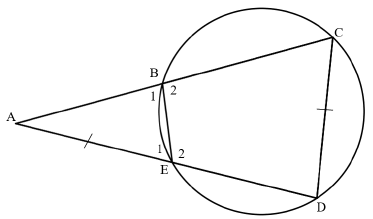
Prove that:
10.1 ΔACD ⫴ ΔAEB (4)
10.2 AC.EB = CD2 (3)
10.3 Hence or otherwise, if AC = 13 cm and EB = 3 cm, calculate the length of CD. (3)
[10]
TOTAL: 150
INFORMATION SHEET

Technical Mathematics Paper 1 Memorandum - Grade 12 June 2021 Exemplars
MARKING CODES | |
A | Accuracy |
AO | Answer only |
CA | Consistent accuracy |
M | Method |
R | Rounding |
NPR | No penalty for rounding |
NPU | No penalty for units omitted |
S | Simplification |
F | Correct formula |
SF | Substitution in correct formula |
MEMORANDUM
QUESTION 1 | ||||
1.1 | 1.1.1 | x2 - 8x - 33 = 0 (8)2 2(1) 4(1) 33 | ? Factors | (3) |
1.1.2 | x2 - 7x = 10 (-3x -1) | ?S A ? SF CA ?both values of x CA | (3) | |
1.1.3 | -2x2 + 9x+ 5 < 0 | ? Factors SF A | (4) | |
1.2 | P = 2(l + w) OR
x = 40, 78 or 4, 22 | ?length in terms of x A ?M (Pyth.) CA
OR
?length in terms of x A | (6) | |
1.3 | x = y+ 3 and y - x2 = -2x - 3 | ? Substitution A ?S CA ? Factors SF CA ? Both y-values CA ? Both x-values CA | ||
OR y = 0 or y = -3 | OR | (5) | |||
? equating Y | A | ||||
? S | CA | ||||
? Factors | CA | ||||
? x-values | CA | ||||
? y-values | CA | ||||
1.4 | 1.4.1 | K = 8 + 32 + 1 = 41 | ? value of K | A | (1) |
1.4.2 | 41 = 1 0 1 0 0 12 | ? 1 0 1 0 0 12 | CA | (1) | |
[23] | |||||
QUESTION 2 | |||
2.1 | Δ = b2 - 4ac < 0 | ?Discriminant < 0 A | (2) |
2.2 | Δ = b2 - 4ac | ? SF A | (4) |
[6] | |||
QUESTION 3 | |||||
3.1 | 3.1.1 |
| ? Exponential form / Eksponensiële vorm ? S | A CA | (2) |
3.1.2 |
OR
| ?Log property ?Exponential form ?S ?Log property
OR
?Log property ?S ?Log property ?Log property | A CA CA CA A CA CA CA | (4) | |
3.2 | -2 (log 25 - log 4) = 4 | ?Exponential form ?Log property ?Factors | A CA CA | (3) | |
3.3 | 3.3.1 |
| ?M ?Exponential property ?Exponential property | A CA CA | (3) | ||
3.3.2 | log3 (x - 3) - log3 5 = 1 OR log3 (x - 3) - log3 5 = 1 | ?Log property ?Log property ?S OR ?Log property ?Log property ?S | A CA CA A CA CA | (3) | |||
3.4 | x - 3(5i + 2) = 4 - 3i + yi OR x - 3(5i + 2) = 4 - 3i + yi | ?S ?x-value ?y-value
OR ?S ?x-value ?y-value | A CA CA
A CA CA | (3) | |||
3.5 | V = 110, 4 + 46,1i | ?Substitution A | (5) |
[23] | |||
QUESTION 4 | |||||
4.1 | 4.1.1 |
| ? SF ?value of r ?value of a | (3) | |
4.1.2 | 0 ≤ y ≤ √10 | ? 0 and √10 CA from 4.1.2 | (2) | ||
4.1.3 | B(-√10;0) | ? Coordinates of B CA from 4.1.1 | (1) | ||
4.1.4 | y= 0 x= 0 | ? x= 0 A ? y= 0 A | (2) | ||
4.2 | 4.2.1 | k(x) = 2( x - 2)2 - 2 OR k(x) = 2( x - 2)2 - 2 | ?Substitution A ?y-int CA OR ?S A | (2) | |
4.2.2 | TP (2; -2) | ?x-coordinate ?y-coordinate | (2) | ||
| 4.2 | 4.2.3 | k(x) = 2 ( x - 2)2 - 2 | ?S A ?Equate to 0 CA ?Factors CA ?Both x-values CA | (4) | |
4.2.4 | x ∈ R | ? x ∈ R A | (1) | ||
4.2.5 | 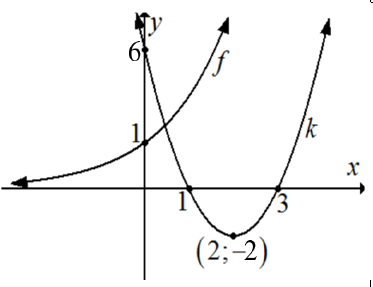 | f: k: | (6) | ||
4.2.6 | y ≥ -2 | ? y ≥ -2 CA | (1) | ||
[24] | |||||
QUESTION 5 | ||||
5.1 | A = P(1+ ni) | ?SF ?S | A CA | (2) |
5.2 | A = P(1+i )n | ?F ?SF ?S | A CA CA | (3) |
5.3 |
| ? SF A ?S CA ? Sum CA ? SF A ?S CA ?Difference CA ?SF CA ?S CA ? SF A ?S CA ? SF A ? S CA ?SF A ?S CA ?S CA ?S CA | (8) | |
[13] | ||||
QUESTION 6 | |||||
6.1 |
| ?F A ?SF CA ?S CA ?S CA ? f '(x) = -2 CA | (5) | ||
6.2 | 6.2.1 |
| ?3a A ?a- 4 CA | (2) | |
6.2.2 |
| ?S A ? x/2 CA ? 3x3 CA
| (3) | ||
6.2.3 | S = ½ ft 2 | ? ft A ? πt CA | (2) | ||
| 6.3 | 6.3.3 | f (x) = 3x2 | ?6x A ?S CA ?Equating derivative and av. gradient CA ? x= 5 CA | (4) |
[16] |
QUESTION 7 | |||||
7.1 | g(x) = x3 - 12x - 16 | ?substitution by -2 A ?S CA | (2) | ||
7.2 | g(x) = x3 - 12x - 16 | ?Equating to 0 A | (4) | ||
7.3 | (0; -16) | ? y-intercept A | (1) | ||
7.4 | f(x) = x3 -12x -16 | ?Derivative A | (6) | ||
7.5 | 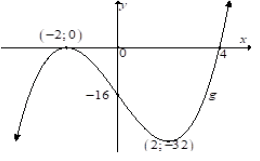 | ?Shape A ?y-intercept CA ?x-intercepts CA ?Both turning points CA | (4) | ||
7.6 | h(x) = (x - 2)3 - 12(x - 2) -16 | ?h(x) A | (1) | ||
7.7 | -2 > x or x < 2 | √ -2 > x CA ? x < 2 CA | (2) | ||
[20] | |||||
QUESTION 8 | |||||
8.1 | 8.1.1 | q = 820 - p | ? q = 820 - p | A | (1) |
8.1.2 | Z= pq | ?Substitution CA | (2) | ||
8.1.3 | Z = 820 p - p2 | ?Derivative = 0 CA ?S CA | (2) | ||
8.2 | 8.2.1 | R ( x) = -50x2 + 3200x -1860 | ?Substitution A | (2) | |
8.2.2 | R (x) = -50x2 + 3200x -1860 = artisan's maximum earnings | ?Derivative = 0 CA ?S CA | (4) | ||
[11] | |||||
QUESTION 9 | |||||
9.1 | 9.1.1 |
| ? 2x½ A | (4) | |
9.1.2 |
| ?S A | (4) | ||
9.2 |
| ?A definite integral formula A | (6) | ||
[14] | |||||
TOTAL: | 150 | ||||
Technical Mathematics Paper 1 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of NINE questions. Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera, which you have used in determining your answers.
- An approved scientific calculator (non-programmable and non-graphical) may be used, unless stated otherwise.
- If necessary, ALL answers should be rounded off to TWO decimal places, unless stated otherwise.
- Number the answers correctly according to the numbering system used in this question paper.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is attached.
- Answer QUESTION 4.2.5 and QUESTION 7.5 on the ANSWER SHEETS provided. Write your name in the space provided and hand in the ANSWER SHEETS with your answer book.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 x2 - 8x - 33 = 0 (3)
1.1.2 x2 - 7x = 10 (-3x+1) (correct to TWO decimal places) (3)
1.1.3 -2x2 + 9x + 5 < 0 (4)
1.2 The diagram below is a rectangle with perimeter equal to 90 cm.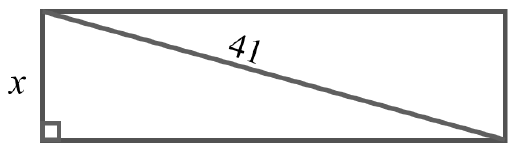
The following formula may be used: Perimeter of a rectangle = 2 (l + w)
Determine the width (x) of the rectangle if the diagonal is 41 cm. (6)
1.3 Solve for x and y simultaneously given that:
x = y+ 3 and y - x2 = -2x - 3 (5)
1.4 Given: K = (1× 23 ) + (1× 25) + 20
1.4.1 Simplify K. (1)
1.4.2 Hence, write K in binary form. (1)
[23]
QUESTION 2
2.1 Given: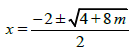
Determine the value(s) of m for which the roots will be non-real. (2)
2.2 Determine the nature of roots of ax2 - bx - 1/a = 0; a # 0; a,b∈Q , given that b = 0. (4)
[6]
QUESTION 3
3.1 Simplify the following WITHOUT using a calculator:
3.1.1 ![]() (2)
(2)
3.1.2 log√65 + log√260 - log13 (4)
3.2 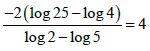 (3)
(3)
3.3 Solve for x:
3.3.1 ![]() (3)
(3)
3.3.2 log3(x - 3) - log3 5 =1 (3)
3.4 Determine the numerical values of x and y if x - 3(5i + 2) = 4 - 3i + yi . (3)
3.5 Convert V = 110, 4 + 46,1i to polar form. (5)
[23]
QUESTION 4
4.1 In the diagram below, the graphs of g and h are defined by ![]() and h (x) = a/x respectively. The point of intersection of g and h is A (1;3).
and h (x) = a/x respectively. The point of intersection of g and h is A (1;3).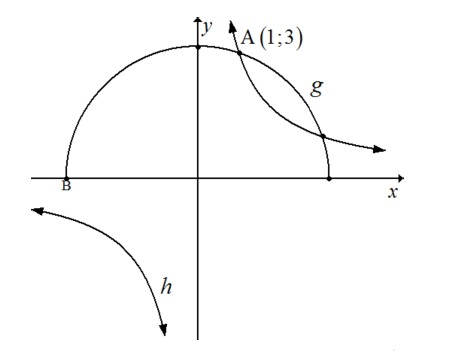
Determine:
4.1.1 The value(s) of a and r (3)
4.1.2 The range of g (2)
4.1.3 The coordinates of point B (1)
4.1.4 The equation of the asymptotes of h (2)
4.2 Given the functions f and k defined by f (x) = 2x and k(x) = 2( x - 2)2 - 2.
4.2.1 Determine the y-intercept of k (2)
4.2.2 Write down the coordinates of the turning point of k (2)
4.2.3 Determine the x-intercepts of k (4)
4.2.4 Write down the domain of f (1)
4.2.5 Sketch the graphs of f and k on the same set of axes on the ANSWER SHEET provided. Clearly show the asymptotes, intercepts with the axes and the coordinates of any turning points. (6)
4.2.6 Write down the range of k. (1)
[24]
QUESTION 5
5.1 Sam hired an angle grinder, as shown in the picture below, at a tool hire shop at a flat rate of 15% per hour plus R35.
Determine how much it will cost to hire the angle grinder for 9 hours. (2)
(2)
5.2 The present population of a small town is 13 565. It is stated that the population grows annually at a compound growth rate of 6,5%. Determine the population size of this town after 8 years. (3)
5.3 Linzo deposited R 120 000,00 in an investment account. She further deposited R50 000,00 into the same account after 12 months. She withdraws R35 000,00 from the same account to pay for repairs to the roof of her house at the end of 2 years.
- The interest rate during the first year is 9% p.a. compounded monthly.
- Thereafter, the interest rate is changed to 8,5% p.a. compounded quarterly.
Calculate the balance of the account after 5 years.(8)
[13]
QUESTION 6
6.1 Determine f'(x) by using FIRST PRINCIPLES if f (x) = -2x+ ¼ (5)
6.2 Determine the following:
6.2.1 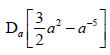 (2)
(2)
6.2.2 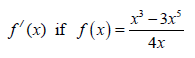 (3)
(3)
6.2.3 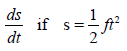 where f is a constant and f = π (2)
where f is a constant and f = π (2)
6.3 Determine the numerical x-value between 2 and 8 such that the instantaneous rate of change of f (x) = 3x2 is equal to the average rate of change over the interval x ∈[2;8]. (4)
[16]
QUESTION 7
Given: g(x) = x3 - 12x - 16
7.1 Show that ( x + 2) is a factor of g. (2)
7.2 Determine the x-intercepts of g. (4)
7.3 Write down the coordinates of the y-intercept of g. (1)
7.4 Determine the coordinates of the turning points of g. (6)
7.5 Sketch the graphs of g on the ANSWER SHEET provided. Show clearly the intercepts with the axes and the coordinates of any turning points. (4)
7.6 Without simplifying the equation, determine the defining equation of h if g (x) is shifted so that the local maximum coincides with (0;0 ). (1)
7.7 Determine the values of x for which g'(x) > 0 . (2)
[20]
QUESTION 8
8.1 The sum of two numbers, p and q, is 820.The greater number is p and the smaller number is q.
8.1.1 Write q in terms of p. (1)
8.1.2 Show that the product, Z, of the two numbers is given by Z = 820 p - p2 . (2)
8.1.3 Determine the value of p if the product Z is a maximum. (2)
8.2 An artisan’s earning ability in rand, R, varies with the artisan’s work experience in years, x, according to the formula:
R (x) = -50x2 + 3200x - 1860
8.2.1 Calculate the artisan’s earnings after 15 years’ work experience. (2)
8.2.2 Determine the maximum earnings of the artisan. (4)
[11]
QUESTION 9
9.1 Determine the integral:
9.1.1 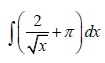 (4)
(4)
9.1.2 ![]() (4)
(4)
9.2 The sketch below shows the shaded bounded area of the curve of the function f defined by f (x) = 4x - x2.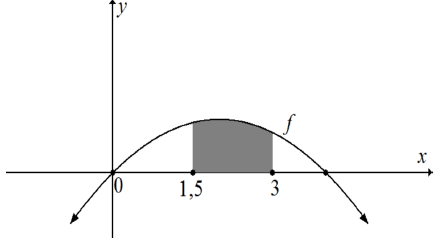
Determine (showing ALL calculations) the shaded area bounded by the curve and the x-axis between the points where x = 1, 5 and x = 3 . (6)
[14]
TOTAAL: 150
INFORMATION SHEET: TECHNICAL MATHEMATICS P1

ANSWER SHEET
QUESTION 4.2.5
QUESTION 7.5
Mathematics Paper 2 Memorandum - Grade 12 June 2021 Exemplars
MEMORANDUM
| QUESTION 1 | ||
1.1 | a = 62 | value of a |
(5) | ||
1.2 | Skewed to the right OR Positively skewed | answer |
(1) | ||
1.3 | Yes | Yes |
(2) | ||
[8] | ||
| QUESTION 2 | |||||||||||||||||||||||||||||||||||||
| 2.1 | Positive impact The number of learners obtaining lower marks decreased while those obtaining higher marks increased in the Post Test. | positive impact reason | (2) | ||||||||||||||||||||||||||||||||||
| 2.2 | 20 < x ≤ 30 | answer | (1) | ||||||||||||||||||||||||||||||||||
| 2.3 | Less | answer | (1) | ||||||||||||||||||||||||||||||||||
| 2.4 | |||||||||||||||||||||||||||||||||||||
| Frequency Cummulative frequency | (4) | |||||||||||||||||||||||||||||||||||
| 2.5 | 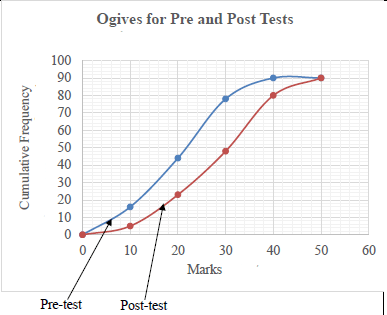 | Grounding Upper limits used Shape | (3) | ||||||||||||||||||||||||||||||||||
2.6 | Pre: 90 – 78 = 12 learners obtained 60% and more | 12 | (3) | ||||||||||||||||||||||||||||||||||
[14] | |||||||||||||||||||||||||||||||||||||
| QUESTION 3 | ||
 | ||
3.1 | t = 2 | value of t |
(1) | ||
3.2.1 |
| substitution answer (2) |
3.2.2 | mPR =y2 - y1 = 0 - 6 | substitution gradient of PR (2) |
3.3 | tan RPS = 6/7 | tanθ = 6/7 |
3.4 | mPR = 6/7 ∴ ΔPRQ is not right angled at R OR RQ2 =100 | substitution OR
substitution |
3.5 | mnewline = mPQ = - 4/7 | gradient of new line | (3) |
3.6 | SP = 7 units | length of SP | (5) |
[22] | |||
| QUESTION 4 | |||
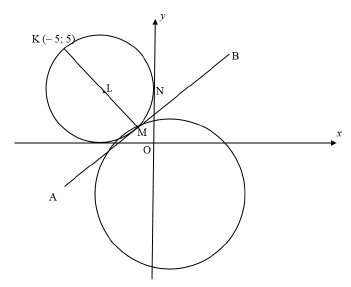 | |||
4.1.1 | x2 + y2 + 6x - 6y + 9 = 0 | method | (4) |
4.1.2 |
| method | (3) |
4.1.3 |
| mLM OR mKM | (4) |
4.1.4 | ( x + 3)2 + ( y - 3)2 = 9 | value of x | (2) |
4.2.1 | L ( – 3 ; 3) | value of x |
4.2.2 | mML/ = -4 - 1 = - 5 Not passing through the origin | mML/ |
[19] |
| QUESTION 5 | ||
5.1.1 |
| value of x |
5.1.2 |
| expansion |
5.1.3 |
| reduction |
5.2.1 | 1- cosθ = 0 or sinθ = 0 OR θ = 360º.k or θ =180º + 360º.k (k∈θ) | method |
5.2.2 |
| common denominator |
| 5.3 | LHS/LK = sin (x - y) | identity |
| [20] | ||
| QUESTION 6 | ||
6.1.1 | 1 | 1 (1) |
6.1.2 | 120° | 120° (1) |
6.2 | f (x) = g(x) | cos(x - 60º) - cos(90º - 3x) |
6.3 | 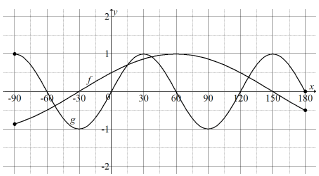 | f: g: |
6.4 | x = -30º or x = 150º | both values of x beide waardes van x |
(1) | ||
6.5 | f (x) = cos(x - 60º + 15º) | h(x) = cos (x – 45°) |
(1) | ||
[15] | ||
| QUESTION 7 | ||
 | ||
52 = 42 + 52 - 2(4)(5) cos A | substitution into cosine rule | (5) |
[5] | ||
| QUESTION 8 | |
 | |
OM ⊥ CD (line from centre which bisects the chord) | S/R |
[5] | |
| QUESTION 9 | ||
 | ||
9.1 | R2 = Q2 ( ∠s in the same segment) | S/R |
9.2 | S2 = T2 = x (∠s in the same seg) | S/R |
9.3.1 | R1 + x + 90º - x = 180º ( sum of ∠s of Δ) | S |
9.3.2 | P = 90º (∠in thesemicircle) | S |
| 9.4.1 | Q2 = T2 = x (∠s opp. equal sides) ∴ Q2 = S2 ∴RS||QT (Alt ∠s are equal) | S/R R (2) |
| 9.4.2 | U2 = Q2 = x VW is a tangent to circle passing through QUT (Converseof tan-chord theorem) | S R (2) |
| [17] | ||
| QUESTION 10 | ||
 | ||
10.1 | Construction: Draw diameter GOE. Join EH | construction |
(5) | ||
10.2 | 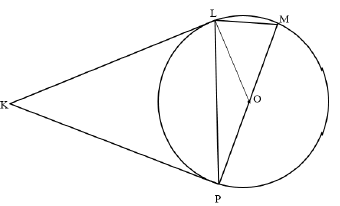 | |
10.2.1 | Kite | answer (1) |
10.2.2 | KLO = 90º (tan ⊥ rad.) | S/R |
10.2.3 | KLO + KPO = 90º + 90º | S |
10.2.4 | K + LOP =180º (Opp.∠sof cyclicquad.) OR M = 67º ( ∠s opp. = sides) | S/R OR S/R |
[18] | ||
| QUESTION 11 | ||
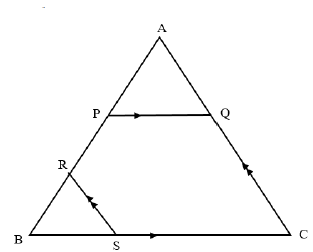 | ||
AP = 3 (Prop. theorem; PQ||BC) | S/R | |
[7] | ||
| TOTAL: | 150 | |
Mathematics Paper 2 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions in the ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The box and whisker diagram below represents soccer clubs’ standings from position 1 to 14 after playing an equal number of games.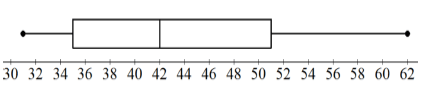
The following table is partly completed, from top (position 1) to bottom (position 14):
Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Points | a | 59 | 58 | b | 49 | 45 | c | 42 | 37 | 36 | d | 32 | 32 | e |
1.1 Write down the values of a, b, c, d and e. (5)
1.2 Comment on the skewness of the data. (1)
1.3 One commentator says the top four teams each had at least 50 points. Do you agree with the commentator or not? Justify your answer. (2)
[8]
QUESTION 2
A school organised a weekend camp for the 90 grade 12 learners doing Mathematics. Learners wrote a pre-test (test before classes started) and a post-test (test after classes finished), out of 50 marks. Below is the graph representing the data.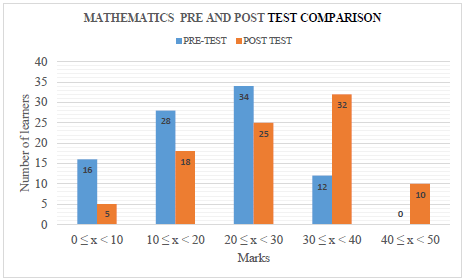
2.1 Use the graph to conclude whether the camp had a positive impact (improved performance) or not. Give a reason for your answer. (2)
2.2 Write down the modal class of pre-test marks. (1)
2.3 Is the mean mark of the pre-test greater than, less than or the same as that of the post-test? (1)
2.4 Complete the frequency and cumulative frequency table in the ANSWER BOOK.
| Marks | Frequency | Cumulative Frequency | ||
| Pre-test | Post-test | Pre-test | Post-test | |
| 0 ≤ x < 10 | ||||
| 10 ≤ x < 20 | ||||
| 20 ≤ x < 30 | ||||
| 30 ≤ x < 40 | ||||
| 40 ≤ x < 50 | ||||
(4)
2.5 Draw the cumulative frequency graphs (ogives) using the grid provided in the ANSWER BOOK. (3)
2.6 The teacher targeted to have 50% more learners to get 60% or more in post-test compared to pre-test. Determine, with the necessary calculations or justification, whether the teacher achieved the target or not. (3)
[14]
QUESTION 3
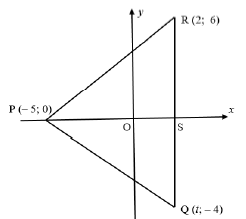
∆RPQ with vertices R(2; 6), P (– 5; 0) and Q(t; – 4) is given below. RQ is perpendicular to the x-axis and cuts the x-axis at S. O is the origin.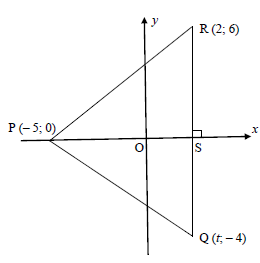
3.1 Write down the value of t. (1)
3.2 Determine:
3.2.1 the length of PR. Leave your answer in simplest surd form. (2)
3.2.2 the gradient of PR. (2)
3.3 Determine the size of PRQ . (5)
3.4 Determine whether ΔQPR is right angled at P or not. (4)
3.5 Determine the equation of the line parallel to PQ and passing through the origin. (3)
3.6 Determine the value of Area of ΔSPR (5)
Area of ΔPRQ
[22]
QUESTION 4
In the diagram below, the smaller circle with diameter KM passing through centre L has a tangent at M and y-intercept at N. The equation of the smaller circle is
x2 + y2 + 6x - 6y + 9 = 0
The bigger circle passes through M. The origin, O and K (– 5 ; 5) is given.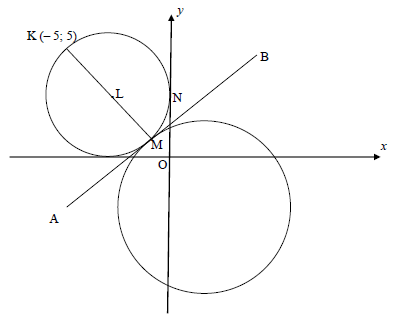
4.1 Determine:
4.1.1 the coordinates of L and the length of the radius of the smaller circle (4)
4.1.2 the coordinates of M (3)
4.1.3 the equation of tangent AMB in the form y = …. (4)
4.1.4 the coordinates of N (2)
4.2 If the coordinates of the centre of the bigger circle is a result of shifting the coordinates of L, 5 units to the right and 7 units down.
4.2.1 Write down the coordinates of the centre of the new circle. (2)
4.2.2 Determine whether the diameter of the bigger circle from a common point of contact M passes through the origin or not. (4)
[19]
QUESTION 5
5.1 Given that sin ∝ = - 5/13 and tan ß = - 3/4 where ∝, ß ∈[90º ;270º] , calculate, without the use of a calculator, the value of:
5.1.1 sin (∝+ ß) (5)
5.1.2 cos 2ß (3)
5.1.3 tan (– ∝ – 180⁰ ) (2)
5.2 Consider the identity:
sin θ - cos θ = 1
1 - cos θ sin θ sin θ
5.2.1 For which value(s) of θ , for θ∈[0º;360º] is the identity undefined? (2)
5.2.2 Prove the identity. (4)
5.3 If tan x = 3k and tan y = 2k, determine sin (x - y) in terms of k (4)
cos x.cos y
[20]
QUESTION 6
Given the functions:
f (x) = cos(x - 60º) and g(x) = sin3x for x∈[ -90º;180º]
6.1 Write down:
6.1.1 the amplitude of f (1)
6.1.2 the period of g (1)
6.2 Determine the values of x for which f(x) = g(x) for x ∈ [– 90° ; 180°] (6)
6.3 On the same set of axes, sketch the graph of f and g for x ∈[–90°; 180°] in the SPECIAL ANSWER BOOK. Show ALL intercepts with the axes as well as turning and end points. (5)
6.4 For which value(s) of x is g(x)/f(x) undefined for x ∈[–90°; 180°]? (1)
6.5 Write down the equation of h(x) if h(x) is a result of shifting f(x), 15⁰ to the left. (1)
[15]
QUESTION 7
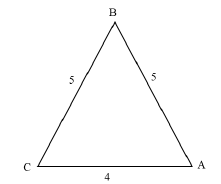
The diagram below shows ΔABC with lengths 5, 5 and 4 units.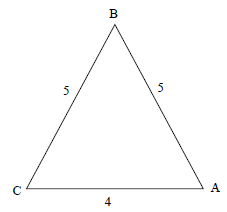
Determine the numerical value of cos A-cos B (5)
[5]
Give reasons for your statements in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
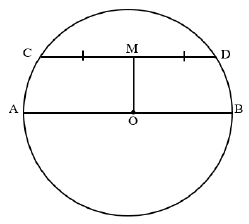
In the diagram below, O is the centre of circle A, B, C and D. M is the midpoint of chord CD. Line OM is drawn. AB is the diameter. AB = 22 cm and OM = 7 cm.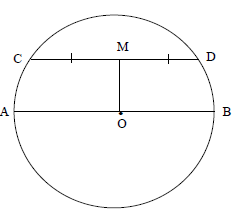
Determine, with reasons, the length of CD. (5)
[5]
QUESTION 9
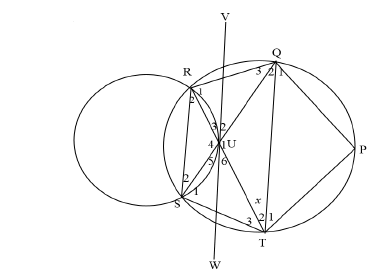
In the diagram below, a bigger circle PQRST intersects a smaller circle at R and S. VW is a tangent of the smaller circle at U. SUQ and TUR are straight lines.
Chords RQ, QP, PT, QT, TS and SR are also drawn. RTQ = x .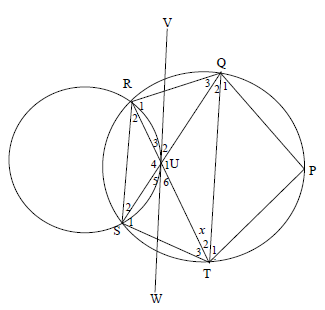
9.1 Prove, with reasons, that ΔRUS ||| ΔQUT. (3)
9.2 Determine, with reasons, THREE other angles each equal to x. (4)
9.3 If RQT = 90° – x , determine :
9.3.1 whether QT is a diameter or not. (4)
9.3.2 P (2)
9.4 If it is further given that UQ = UT, show that:
9.4.1 RS || QT (2)
9.4.2 VW is also a tangent to the circle passing through QUT at U. (2)
[17]
QUESTION 10
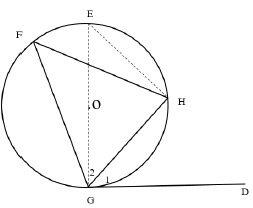
10.1 In the diagram below, O is the centre of circle FGH with DG a tangent at G.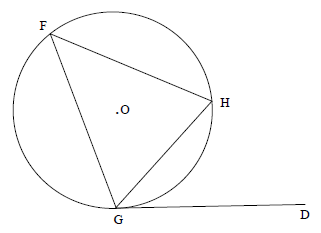
Prove the theorem which states that DGH = F. (5)
10.2 In the diagram below, O is the centre of circle LMP with tangents KL and KP at L and P respectively. OLM = 67º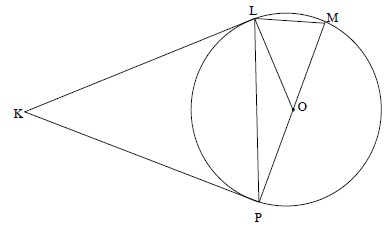
10.2.1 What type of quadrilateral is KLOP? (1)
10.2.2 Give, with reasons, 3 angles each equal to 90°. (5)
10.2.3 Prove, stating reasons, that KLOP is a cyclic quadrilateral. (2)
10.2.4 Hence, determine K . (5)
[18]
QUESTION 11
In the diagram below, ∆ABC is drawn with PQ || BC and RS || AC.
AQ : QC = 3 : 5 and BR : RA = 1 : 3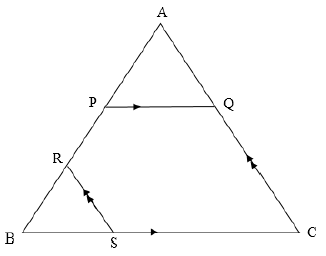
Prove that AP = PR. (7)
[7]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS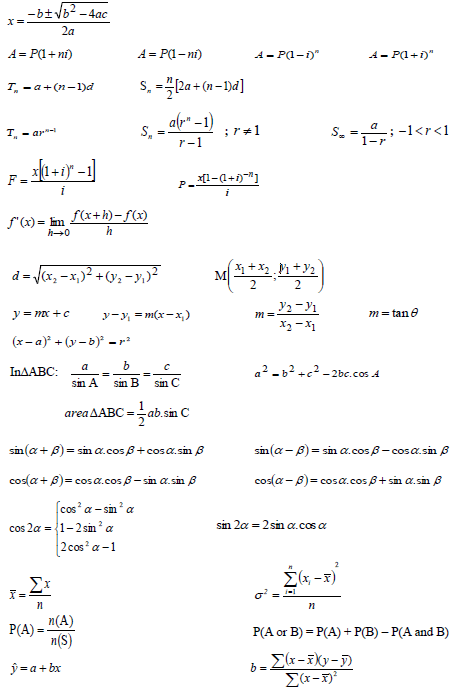
Mathematics Paper 1 Memorandum - Grade 12 June 2021 Exemplars
NOTE:
- If a candidate answered a question TWICE, mark the FIRST attempt ONLY.
- Consistent accuracy (CA) applies in ALL aspects of the marking guideline.
- If a candidate crossed out an attempt of a question and did not redo the question, mark the crossed-out attempt.
- The mark for substitution is awarded for substitution into the correct formula.
QUESTION 1 | ||
1.1.1 | 2x(x +1) = 0 | x = 0 |
1.1.2 | 2x(x - 3) = 1 Penalise 1 mark for incorrect rounding off. | standard form |
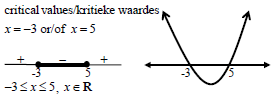
1.1.3 | x2 - 2x - 15 ≤ 0 | factors OR x ∈[-3 ; 5] (3) |
1.1.4 |
| 3 + a - 2√a | (3) |
1.2 | x - 2 y = 3 .......................(1) | x = 2y + 3 | (6) |
1.3.1 | For equal roots Δ = 0 | Δ = 0 | (4) |
1.3.2 | Consider axis of symmetry | method | (2) |
[24] | |||
QUESTION 2 | |||
2.1 | 23 ; 21 ; 19 ; . . . ; – 47 | substitution | (2) |
2.2.1 | T2 - T1 = T3 - T2 | method | (3) |
2.2.2 |
| first term and common difference
| (4) |
2.3.1 | 25 ; 48 ; 69 ; 88 ; x ; y | √ x = 105 | (2) |
2.3.2 | 2a = -2 3a + b = 23 a + b + c = 25 | value of a | (4) |
2.3.3 | n = -b = -(26) = 169 | method | (3) |
2.4 |
| expanding answer | (2) |
[20] | |||
QUESTION 3 | |||||
3.1 | Alevel1 = 1 × πR2 OR a = πR2 ; r = ½ OR Alevel 4 = 8 × π(1/8R)2 | √√√ Areas for levels 1 to 3 answer value of a value of r substitution | (4)
(4) | ||
3.2 |
| formula | (3) | ||
[7] | |||||
QUESTION 4 | ||||
4.1 | -x2 - 4x + 5 = 0 | solving for x-intercepts | (4) | |
4.2 | x = (-5 + 1) = -2 or x = -(-4) = -2 | x-value | (3) | |
4.3 | a = 1 and q = 5 | a = 1 | (2) | |
4.4 | Length of ND = 9 (from 4.2) | ND = 9 TD = 3 NT = 6 | (3) | |
4.5 | S( -4 ; 5) m = f'(-4) | coordinates of S | (5) | |
[17] | ||||
QUESTION 5 | |||
5.1 | A(1 ; 0) | answer | (1) |
5.2 | f (x) = k g(x) = log p x 2 = logp 9 | k = 6 p2 = 9 | (3) |
5.3 | y = log3x | interchanging x and y | (2) |
5.4 | Range of g -1 | √√ answer | (2) |
5.5 | 6 = log3x + 1 | (3 ; 1) point on g | (2) |
[10] | |||
QUESTION 6 | |||
6.1 | g(x) = (x + 2)( y + 3) = k | standard form | (3) |
6.2 | - 5 = k - 3 2 0 + 2 1 = k 2 2 | substitution | (2) |
6.3 | y = -(x + 2) - 3 | substitution | (2) |
[7] | |||
QUESTION 7 | |||
7.1 |
| formula substitution
| (3)
(3) |
| 7.2 | 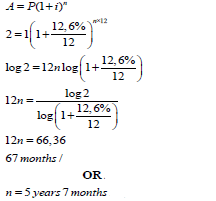 | substitution use of logs solving for n answer | (4) |
| 7.3 |  | ||
= R73762,18 |
subtraction | ||
QUESTION 8 | ||
8.1 |
Answer only = 0 marks | −7?2 − 14?ℎ − 7ℎ2 |
8.2.1 |
| √ x-4 + x½ |
8.2.2 |
| (x½ + 2)(x½ - 2) |
[10] | ||
QUESTION 9 | ||||
9.1 | g(-5) = (-5)3 + (-5)2 -16(-5) + 20 | substitution | (2) | |
9.2 | g(x) = x3 + x2 -16x + 20 | (x2 - 4x + 4) | (3) | |
9.3 | g'(x) = 3x2 + 2x -16 = 0 | g'(x) | (4) | |
9.4 | 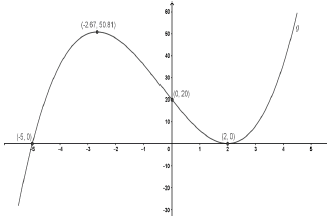 | intercepts with the axes | (3) | |
9.5 | g''(x) = 6x + 2 OR g''(x) = 6x + 2 = 0 | g''(x) substitution conclusion g''(x) x = - 1/3 conclusion | (3) | |
9.6 |
OR -8/3 ≤ x ≤ 0 or x ≥ 2 |
| (3) | |
[18] | ||||
QUESTION 10 | ||||
10.1 |
| multiplication | (2) | |
10.2 | 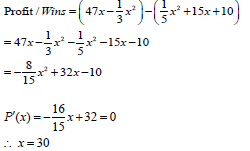 | method | (5) | |
[7] | ||||
QUESTION 11 | |||
11.1.1 | P( A or B) = P( A) + P(B) - P( A and B) | P(B) = 0,4 | (3) |
11.1.2 | P( A and/en B) = 0, 2 | P(A) x P(B) = 0,2 | (3) |
11.2.1 | P(R or G) = 1 OR (100%) | answer | (1) |
11.2.2 | 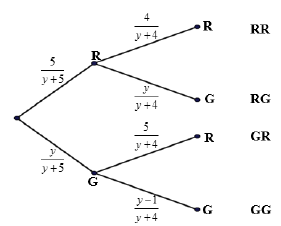 | first branch with labels second branch with labels third branch with labels outcomes | (4) |
11.2.3 |
| method | (5) |
[16] | |||
TOTAL: | 150 | ||
Mathematics Paper 1 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions. Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet, with formulae, is included at the end of the question paper.
- Number the answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x, in each of the following:
1.1.1 2x ( x +1) = 0 (2)
1.1.2 2x(x - 3) =1 (correct to TWO decimal places) (4)
1.1.3 x2 - 2x -15 ≤ 0 (3)
1.1.4![]() (3)
(3)
1.2 Solve simultaneously for x and y in the following equations:
x - 2 y = 3
4x2 - 5xy = 3 - 6 y (6)
1.3 The equation 3mx2 - px + 5 = 0 ; m # 0 and p # 0 , has equal roots.
1.3.1 Show that f (x) = 3mx2 - px + 5 has a minimum value. (4)
1.3.2 If it is further given that p < 0 , draw a sketch graph of f (x) = 3mx2 - px + 5 . (2)
[24]
QUESTION 2
2.1 Determine which term of the sequence: 23; 21; 19; . . . is - 47. (2)
2.2 The first three terms of an arithmetic sequence are: 3x - 1 ; x + 5 ; 2x - 4
2.2.1 Calculate the value of x. (3)
2.2.2 Determine the number of terms of which the sum is equal to zero. (4)
2.3 Given the quadratic pattern: 25 ; 48 ; 69 ; 88 ; x ; y ; . . . Determine:
2.3.1 The values of x and y (2)
2.3.2 The general term, Tn of the quadratic pattern (4)
2.3.3 The value of the largest term of this pattern (3)
2.4 Calculate the value of a, if: 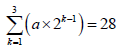 (2)
(2)
[20]
QUESTION 3
A circular disk of radius, R is cut out of paper as shown in the diagram. Two disks of radius, ½R are cut out of paper and placed on top of the first disk, as shown. Then four disks of radius, ¼R are cut out of paper and placed on top of the two disks, as shown.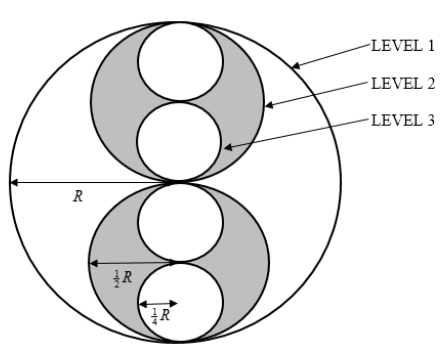
3.1 If this process can be repeated, determine the area of the disks on the fourth level only. (4)
3.2 Calculate the total area of all the disks, if the process is repeated indefinitely. (3)
[7]
QUESTION 4
Given: f (x) = -x2 - 4x + 5 and g(x) = ax + q. E, M and P are the intercepts of the graphs with the axes. N is the turning point and NTD the axis of symmetry of f . T is a point on the graph of g and S is the reflection of M about the axis of symmetry.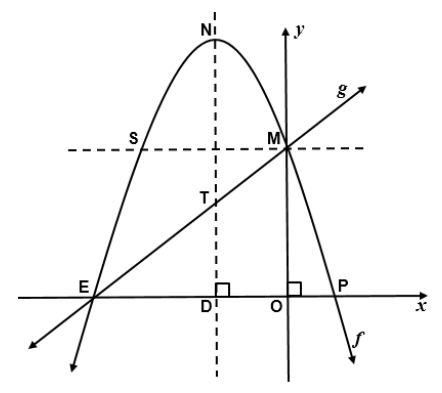
Determine:
4.1 The coordinates of M, E and P (4)
4.2 The coordinates of N (3)
4.3 The values of a and q (2)
4.4 The length of NT (3)
4.5 The equation of the tangent to f at point S (5)
[17]
QUESTION 5
In the figure below, two sketch graphs are shown for: f (x) = k/x , where x > 0 and g(x) = log p x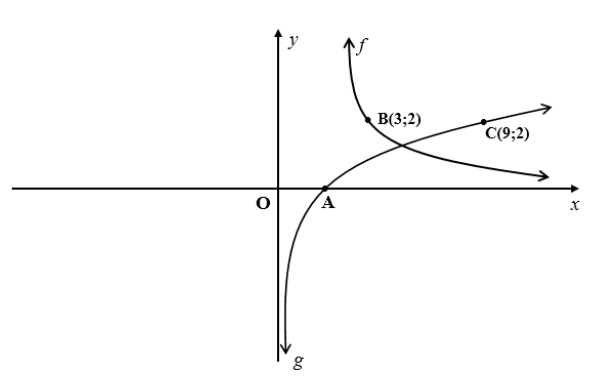
5.1 Write down the coordinates of A. (1)
5.2 Determine the values of k and p. (3)
5.3 Determine the equation of g -1 in the form y = ... (2)
5.4 Write down the range of g -1 . (2)
5.5 Solve for x if 6 - log3x = 1 (2)
x
[10]
QUESTION 6
Given: g(x) = (x + 2)(y + 3) = k ; for k > 0 , is a hyperbola with g(0) =- 5/2 . Determine:
6.1 The equations of the asymptotes of g (3)
6.2 The value of k (2)
6.3 The equation of the axis of symmetry of g which has a negative gradient (2)
[7]
QUESTION 7
7.1 Convert a nominal interest rate of 8,9% a. compounded monthly to effective interest rate per annum. (3)
7.2 Alan retires and decides to invest R1 000 000 of his retirement lump sum. The bank offers him an interest rate of 12,6% a. compounded monthly. How long will it take for his money to double? (4)
7.3 R60 000 is invested in an account which offers interest at 7% a. compounded quarterly for the first 18 months. Thereafter the interest rate changes to 5% p.a. compounded monthly. Three years after the initial investment, R5 000 is withdrawn from the account. How much money will be in the account at the end of 5 years? (7)
[14]
QUESTION 8
8.1 Given f (x) = -7x2. Determine f'(x) from first principles. (4)
8.2 Determine dy if:
dx
8.2.1 y = 1 + √x (3)
x4
8.2.2 y = x - 4 (3)
x½ - 2
[10]
QUESTION 9
Given: g(x) = x3 + x2 -16x + 20
9.1 Show that (x +5) is a factor of g(x). (2)
9.2 Hence, or otherwise determine the x-intercepts of g. (3)
9.3 Determine the coordinates of the turning points of g. (4)
9.4 Sketch the graph of g(x), showing clearly the intercepts with the axes and the turning points. (3)
9.5 Discuss the concavity of the graph at the y-intercept. Support your answer with relevant (3)
9.6 For which values of x will x. f'(x) ≥ 0? (3)
[18]
QUESTION 10
The total cost of producing x cellphones per day is given by 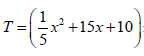 rand and each cellphone is sold for a price of
rand and each cellphone is sold for a price of 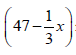 rand.
rand.
10.1 Determine an expression for money raised from the sale of x (2)
10.2 How many cellphones should be made daily to maximise the profit? (5)
[7]
QUESTION 11
11.1 Given:
- P(A) = 0,5
- P(A and B) = 0, 2
- P(not B) = 0,6
11.1.1 Determine P(A or B) (3)
11.1.2 Your teacher claims that events A and B are independent. Do you agree or disagree? Justify your answer with (3)
11.2 A bag contains five red and y green marbles.
11.2.1 What is the probability that a red or a green marble will be drawn from the bag? (1)
11.2.2. Two marbles are drawn successively without Represent this using a tree diagram. Label all the branches and write down the outcomes. (4)
11.2.3 Determine how many green marbles are in the bag if the probability of drawing two marbles of the same colour is 31/66 .(5)
[16]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS
History Paper 2 Errata - Grade 12 September 2021 Preparatory Exams
The History P2 Grade 12 September was written on Tuesday, 14 September 2021. We were made aware of certain amendments and omissions that were discovered during the marking process.
In order to address this and to ensure that learners are not disadvantaged, the following standardised approach to marking must be adopted across the Province. The following guidelines regarding marking was prepared in conjunction with the examiner and moderator.
ERRATA
QUESTION NUMBER | ERRATA |
| 2.3.1 | The rights of all human beings to be treated equally and with dignity |
| 2.3.3 |
|
| 2.3.4 | To pursue criminal prosecution |
2.5 | Source 2C should be changed to Source 2D and Source 2B changed to Source 2D |
2.6 | The TRC offered full amnesty .. (Source 2C) TRC provided a platform..... (Source 2C) Deetlefs revealed ...... (Source 2C) Jill Burger revealed ..... (Source 2D) The family had no choice (Source 2D) |
3.2.2 |
|
3.2.3 | Remove the bullet: the unemployment rate increased to 1,7 million |
Geography Paper 1 Errata - Grade 12 September 2021 Preparatory Exams
The Geography P1 Grade 12 September was written on Tuesday, 31 August 2021. We were made aware of certain amendments and omissions that were discovered during the writing process.
In order to address this and to ensure that learners are not disadvantaged, the following standardised approach to marking must be adopted across the Province. The following guidelines with regard to marking was prepared in conjunction with the examiner and moderator.
ERRATA
There was an unintended error in QUESTION 3 (3.2 and 3.4.3) in Geography P1. The alphanumeric grid did not correspond with the symbols referred to in these respective questions. A total of 7 marks could have been potentially compromised here. Most Grade 12 learners would still have been able to source the symbols referred to in the map and answered these sub-questions.
However, if there were learners that were 'confused' or unfairly prejudiced by this we propose the following:
- Questions 1 and 2 to be marked as per normal out of 120.
- Question 3 to be marked out of 23 MARKS, and the mark converted to 30 as indicated on the SLIDING SCALE below. (Questions 3.2 and 3.4.3 must not be marked at all.)
- Total mark for Geography would then be calculated out of 150 marks.
The examination panel stresses that this must only apply to schools where learners were unable to answer these sub-questions based on the incorrect alphanumeric grid.
Schools who had no issue with this should mark the paper as normal out of 150.
Total Mark out of 23 | Converted mark from 23 to 30 |
23 | 30 |
22 | 29 |
21 | 27 |
20 | 26 |
19 | 25 |
18 | 23 |
17 | 22 |
16 | 21 |
15 | 20 |
14 | 18 |
13 | 17 |
12 | 16 |
11 | 14 |
10 | 13 |
9 | 12 |
8 | 10 |
7 | 9 |
6 | 8 |
5 | 7 |
4 | 5 |
3 | 4 |
2 | 3 |
1 | 1 |
We request that this must be brought to the attention of all educators marking these papers and sincerely apologise for the inconvenience.
Tourism Memorandum - Grade 12 September 2021 Preparatory Exams
MEMORANDUM
SECTION A: SHORT QUESTIONS
QUESTION 1
1.1
1.1.1 C
1.1.2 B
1.1.3 A
1.1.4 D
1.1.5 B
1.1.6 D
1.1.7 C
1.1.8 C
1.1.9 D
1.1.10 B
1.1.11 C
1.1.12 C
1.1.13 D
1.1.14 A
1.1.15 A
1.1.16 A
1.1.17 B
1.1.18 B
1.1.19 A
1.1.20 B (20 x 1) (20)
1.2
1.2.1 Market share
1.2.2 Cash
1.2.3 Colosseum
1.2.4 CCTV cameras
1.2.5 Repeat visits (5 x 1) (5)
1.3
1.3.1 red
1.3.2 summer
1.3.3 jet fatigue
1.3.4 Central Africa
1.3.5 5 (5 x 1) (5)
1.4
1.4.1 C (The Sphinx)
1.4.2 F (The Berlin Wall)
1.4.3 A (ǂKhomani Cultural Landscape)
1.4.4 E (Statue of Christ the Redeemer)
1.4.5 G (Mapungubwe Cultural Landscape) (5 x 1) (5)
1.5
- A (Flight lands on runway 03L/21R at ORTIA)
- D (Passenger enters airside of ORTIA)
- E (Passenger reports to immigration control)
- B (Passenger collects luggage at baggage carousel)
- C (Passenger passes through customs) (5 x 1) (5)
TOTAL SECTION A: 40
SECTION B:
MAP WORK AND TOUR PLANNING; FOREIGN EXCHANGE
QUESTION 2
2.1
2.1.1
- Washington DC, USA -5
Geneva, Switzerland +1 (15:00 on 3 March 2021)
Time difference: 6 hours
15:00 – 6 hours = 09:00 on 3 March 2021
OR
- 09:00 on 3 March 2021 (4)
2.1.2 Geneva, Switzerland +1 (15:00 on 3 March 2021)
Canberra, Australia +10 (+ 1 hour DST = +11)
Time difference: 10 hours
15:00 +10 hours = 25:00 – 24 hours
= 01:00 on 4 March 2021
OR
- 01:00 on 4 March 2021 (5)
2.1.3
- Mumbai, India +5.5
Johannesburg, South Africa +2
Time difference: 3 ½ hours (or 3 hours 30min.)
04:30 –3 ½ hours = 01:00 on 31 January 2021
01:00 +15 hrs 15 min = 16:1531 January 2021
OR
16:15 on 31 January 2021 (6) -
- Insomnia
- Fatigue
- Irritability
- Interrupted sleep
- Discomfort in legs and feet
- Struggle to concentrate
- Constipation or diarrhoea
- Confusion and disorientation
- Dehydration
- Headaches
- Nausea
- Loss of appetite
- Dizziness (3 x 1) (3)
- Customs controls the flow of goods in and out of a country.
Customs is responsible for the collection and safekeeping of customs duties (taxes) in a country.
Customs enforces the laws that govern the import and export of goods to and from the country. (2)
2.2
2.2.1 B / Passport (2)
2.2.2 A health certificate is a statement signed by a health-care provider (such as a doctor or nurse) that verifies the health of the bearer of the certificate or verifies that the bearer of the certificate has had certain vaccinations. (2)
2.2.3
- The traveller in possession of the vaccine passport will not infect other people with Covid-19 should he/she encounter other people.
- The traveller in possession of the vaccine passport will not become infected with Covid-19 should he/she encounter other people.
- The vaccine passport will result in an increase in travel as travel restrictions in place due to Covid-19 will be lessened. (4)
2.3
2.3.1 Business tourist
- MECE tourist (1)
2.3.2
- Delegates’ temperature will be scanned with a thermal scanner on arrival at the hotel and/or Conference Centre.
- Delegates will be required to complete a screening questionnaire on arrival.
- Delegates will be required to exercise sanitising and disinfecting practices.
- Delegates will be required to wear masks except when eating or drinking.
- Seating will be spread out to ensure that a 1,5 metre social distancing is maintained.
- The number of delegates must not exceed 50% of the venue’s normal capacity.
- Menus and service standards must be adjusted and aligned to health and safety protocols and Government regulations. (2 x 2) (4)
[33]
QUESTION 3
3.1
- R45 000 ÷16,98 = €2 650,18
OR
€2650,18 (3)
3.2
- €23 x16,39 = R376,97
OR
R376,97 (3)
3.3
3.3.1
- R175 000 ÷ 13,87 = $12 617,16
OR
$12 617,16 (3)
3.3.2
- R175 000 ÷ 19,77 = £8 851,80
OR
£8 851,80 (3)
3.3.3 USA
- United States of America (1)
3.4
- When the value of the Rand is low in relation to the US Dollar international tourism from the USA to South Africa will increase.
USA tourists will perceive South Africa as a cheap destination. - When tourists from the USA visit South Africa, they will be in a position to spend more money as they will receive more Rand when exchanging their currency.
- They could lengthen their length of stay or participate in more expensive activities while in South Africa.
- They could book into more expensive accommodation as they have more Rand than they would have had if the Rand had been in a stronger position. (4)
[17]
TOTAL SECTION B: 50
SECTION C: TOURISM ATTRACTIONS; CULTURE AND HERITAGE TOURISM; MARKETING
QUESTION 4
4.1
4.1.1
- A – Black Forest
- B – Sydney Opera House
- C – Great Wall of China
- D – Leaning Tower of Pisa
- E – Ayers Rock / Uluru-Kata Tjuta National Park
- F – Niagara Falls (6 x 1) (6)
4.1.2
- 4 (2)
- Australia (2)
- Hiking
- Walking
- Mountain biking
- Skiing
- Snowboarding
- Swimming in lakes
- Boating (2)
4.2
4.2.1 Overcrowding
- Mass tourism
- The total number of tourists received daily is greater than the total number of inhabitants of the city. (2)
4.2.2 The historic city is built on wooden platforms anchored into 118 small islands in a lagoon linked by canals and bridges.
- Venice is famous for its architecture and art, for example, narrow streets, canals, bridges, palaces, churches, monuments, museums and art galleries.
- Apart from walking, water is the main mode of transportation that is widely used by locals and tourists in Venice.
- Venice is one of the most beautiful cities in the world. (2)
4.2.3 Fast-food packaging waste contributed to an increase in litter.
Water pollution was caused by fast-food packaging waste being dumped in the canals.
- The convenience of fast-food outlets influenced tourists not to support traditional Venetian sit-down restaurants.
- Tourists sat eating on bridges, narrow alleys, house doors, and shop windows blocking even further the already overcrowded city.
- The numerous fast-food outlets harmed the cultural heritage character of the city.
- Fast-food packaging waste attracts seagulls looking for food. (2 x 2) (4)
4.2.4
- The ban on cruise ships will reduce water and air pollution in the Venice lagoon and canal.
- It will reduce the damage to the foundations of the buildings that was caused by the movement of water by cruise ships.
- The water quality of the lagoon and canals will improve. (2 x 2) (4)
[24]
QUESTION 5
5.1 IsiMangaliso Wetland Park (2)
5.2 KwaZulu-Natal (2)
5.3
5.3.1
- Beaches
- Dunes
- Lakes
- Swamps
- Reed and papyrus wetlands (3 x 2) (6)
5.3.2 Create international awareness of South Africa’s World Heritages Sites.
Encourage the youth and local population to preserve their cultural and natural heritage.
- Increased visitor numbers to the province/area where the World Heritage Sites are located.
- Job opportunities will be created due to increased demand for products and services.
- Influx of visitors to visit the sites will lead to increased tourism revenue.
- Higher visitor numbers to these sites will increase South Africa's GDP.
- Higher visitor numbers will set the multiplier effect into motion.
- Attract foreign investment.
- A sense of ownership / pride of the heritage within the local community.
- Encourage closer working relationships between all stakeholders.
- Will attract more special interest tourists to South Africa.
- Create more opportunities for entrepreneurship. (2 x 2) (4)
[14]
QUESTION 6
6.1 UK and Ireland
- UK
- United Kingdom
- Ireland (2)
6.2 The shared photos would create an awareness of South Africa as a travel destination during the Covid-19 pandemic.
The shared photos could lead to an increase in new arrivals from UK and Ireland once travel restrictions are lifted.
- Previous visitors from the UK and Ireland might consider returning to South Africa when travel restrictions are lifted. (2 x 2) (4)
6.3 The Tourism Levy South Africa (TOMSA), a private sector initiative, collects a 1% Tourism Levy, voluntarily paid by customers, from participating tourism businesses, for example tour operators, car rental companies and accommodation establishments.
The Tourism Business Council of South Africa (TBCSA) administers TOMSA.
The TBCSA ensures that the collected funds are made available to SATourism for marketing. (3 x 2) (6)
[12]
TOTAL SECTION C: 50
SECTION D:
TOURISM SECTORS; SUSTAINABLE AND RESPONSIBLE TOURISM
QUESTION 7
7.1 Contract of employment (1)
7.2 Employees should sign a contract of employment so that they are aware of the employers’ expectations.
- The signing of a contract of employment protects employees against unfair practices in the workplace.
- The signing of a contract protects the employer should the employee dispute any conditions of employment. (2)
7.3 Code of conduct of Penika Airways (1)
7.4 A code of conduct sets out what is important to a business (its ethics and principles) and prescribes how staff should behave while at work.
It helps to identify and state clearly which behaviour is welcome and which is not.
- It provides the staff with guidelines regarding creation of a co-operative, collaborative atmosphere and promotion of integrity in the workplace.
- A code of conduct is a document that provides guidance to staff about what acceptable behaviour is in the workplace.
- It guides the relationship staff should have with their colleagues and clients.
- It ensures that all at the workplace are treated with respect.
- It acknowledges different religious, cultural and social practices. (2 x 2) (4)
7.5 The CEO was justified in being unhappy about Susan complaining to passengers about her shift as she acted in an unprofessional manner by complaining to passengers. (2)
7.6 The cabin crew has to deal with the challenges of passengers with many differing needs and expectations.
- Cabin crews have to work long hours, are on their feet most of the time while acting in a professional manner.
- Cabin crews have to fly to many destinations in the course of their work which can be demanding. (2)
[12]
QUESTION 8
8.1 Sustainability
Fair share
- Democracy
- Respect
- Transparency
- Reliability (2 x 1) (2)
8.2 A destination that is Fair Trade Tourism accredited will attract environmentally conscious tourists. This could lead to an increase in visitor numbers.
A destination that is Fair Trade Tourism accredited will encourage positive word of mouth advertising.
- A destination that is Fair Trade Tourism accredited could attract investment from likeminded investors. (4)
8.3
8.3.1
- Reuse
- Reduce
- Recycle (2)
NOTE: Accept suitable examples of practices.
8.3.2
- Limit water usage
- Ensure that no taps leak.
- Collect rainwater for reuse.
- Use greywater where possible. (2)
8.3.3
- Install solar panels
- Install wind turbines (2)
8.4 People should be educated about protecting our planet because:
- This will lead to conservation of the planet’s resources for future generations.
- This will ensure that our resources are maintained and not depleted.
- This will create an awareness of conservation.
- Environmental conservation will assist in reducing our collective carbon footprint. (2)
8.5
8.5.1 Mashovhela Lodge can put programmes in place that acknowledge the local culture and heritage.
- They can become involved in social upliftment programmes.
- Provision of medical facilities and staff to attend to the needs of the local community.
- Provision of funded education facilities for the local community.
- Skills development for members of the local community. (2)
8.5.2 Mashovhela Lodge can:
Implement community shareholding in the business.
- Create employment opportunities paying decent wages.
- Ensure the development of supplier businesses from the local community.
- Implement a fair recruitment process.
- Practice local procurement.
- Ensure that their corporate social investment programme financially advantages the local community. (2)
[18]
TOTAL SECTION D: 30
SECTION E: DOMESTIC, REGIONAL AND INTERNATIONAL TOURISM; COMMUNICATION AND CUSTOMER CARE
QUESTION 9
9.1
9.1.1 The G7 summit will focus the world's media and TV on Cornwall providing exposure to a global audience.
- Media personnel from all over the world will visit Cornwall to report on the event.
- Increased marketing for Cornwall as a result of the global media coverage.
- The host country receives worldwide exposure/publicity before, during and after the event. (2)
9.1.2 Potential transport disruptions such as road closures in areas around the venues being used for the event, roadblocks, disruption of train schedules.
Influx of international visitors.
- The deployment of additional police officers to boost the existing local police teams.
- High levels of security around the visiting world leaders.
- The possible threat of G7 protests.
- Schools might have to close for G7 Summit over protest and disruption fears.
- Possible disruption to business operations caused by the summit.
- Fears that there would be a spike in Covid-19 infections because of hosting this summit.
- Fears that the infrastructure will not cope.
- Restricted public access to Carbis Bay beach for the duration of the summit.
- Closure of all venues used for the G7 summit to the public. (2 x 2) (4)
9.1.3 Global measures introduced to contain the virus led to a stop of tourism activities around the world.
- Tourism businesses suffered a major loss in revenue due to the dramatic decrease in international tourist arrivals.
The Covid-19 pandemic resulted in permanent job losses or reduced working hours for employees in the tourism sector. - The cancellation and postponement of trips by tourists resulted in a loss of foreign exchange earnings.
- Loss in tourism revenues had a negative impact on GDP growth.
- Many tourism businesses went bankrupt. (3 x 2) (6)
9.2
9.2.1
- R100 billion
- R100 bn
- 100 billion
- 100 bn (2)
9.2.2 2016 (2)
9.2.3 Above and below line promotional techniques
Special offers
- Discounts offered for bulk purchases.
- Packaging of multiple tourism products.
NOTE: Accept examples of marketing techniques. (4)
[20]
QUESTION 10
10.1 Web-based
- Online
- Internet (2)
10.2 Offers valuable guidance from people who have used a service or product.
- Assists consumers in their decision-making about which businesses to support.
- Provides information about the trustworthiness of a business.
- Provides information about the quality of service that can be expected. (2)
10.3 The image of the business will be damaged.
- The customer will not return to support the business as the complaint was not resolved quickly and efficiently.
Other consumers will see that TikaThai does not care about its customers. - It could lead to bad word-of-mouth publicity for TikaThai.
- Prospective customers will think twice about supporting TikaThai. (3 x 2) (6)
[10]
TOTAL SECTION E: 30
GRAND TOTAL: 200