Adele
Mathematical Literacy Paper 1 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions. Answer ALL the questions.
- 2.1 Use the ANSWER SHEET to answer QUESTION 2.1 3.
2.2 Write your NAME and GRADE in the spaces provided on the ANSWER SHEET FOR QUESTION 2.1.3
Hand in the ANSWER SHEET with your ANSWER BOOK. - Number the answers correctly according to the numbering system used in this question paper.
- Diagrams are not necessarily drawn to scale, unless stated otherwise.
- Round off ALL final answers according to the context used, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Start EACH question on a NEW page.
- Show ALL calculations clearly.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 TABLE 1 below shows some facts relating to Joy who sells sweets at school during break and lunch times.
TABLE 1: JOY’S SALES
50 sweets per packet | 2 packets sold daily |
Cost of one sweet | R0,70 VAT inclusive |
Selling price of one sweet | R1,00 VAT inclusive |
Profit on one sweet | R0,30 |
Use the above information and Value Added Tax (VAT) at 15% to answer the questions that follow.
1.1.1 Explain the meaning of VAT inclusive price. (2)
1.1.2 Calculate the percentage profit Joy makes on ONE sweet. (2)
1.1.3 Calculate Joy’s daily profit from her sales. (2)
1.2
The electricity tariffs in the municipality area where Jane lives is charged according to usage on a sliding scale indicated by BLOCKS in the table below. | |
Block number and kWh | Price (cent/kWh) |
BLOCK 1: (≤ 50 kWh) | 96,61 |
BLOCK 2: (>50 kWh- ≤ 400 kWh) | 125,21 |
BLOCK 3: (>400 kWh- ≤ 600 kWh) | 206,56 |
BLOCK 4: (>600 kWh) | 354,85 |
1.2.1 Calculate the rate (in Rands) that Jane paid for the first 50 kWh she used in May 2021. (2)
1.2.2 Determine the total amount that Jane paid for the first 50 kWh used. (2)
1.2.3 Determine the maximum number of kWh to be paid for in the second block. (2)
1.3 Electricity generated by different sources in South Africa in 2016 are shown in the pie chart below.
PIE CHART SHOWING ELECTRICITY GENERATED BY DIFFERENT SOURCES IN SOUTH AFRICA IN 2016: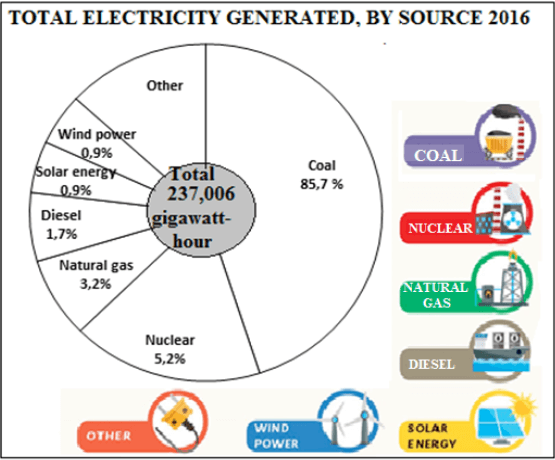
[Source: Old Mutual Wealth & Investments, STATS SA. 2016]
1000 000 Kilo Watt hour (KWh) = 1 Gigawatt hour (GWh)
Use the above information to answer the questions that follow.
1.3.1 Calculate the percentage of electricity generated from other sources. (2)
1.3.2 Determine the Gigawatt hour (GWh) generated from natural gas. (2)
1.3.3 Express the ratio of the energy generated from nuclear to diesel. (2)
1.3.4 Convert the total Gigawatt hour generated by all sources in 2016 into KWh. (3)
[21]
QUESTION 2
2.1
Funda SSS is to select an option to use for photocopying and printing of monthly tests for learners in various grades. TABLE 3: COST OF PRINTING OPTIONS | |||||
No of copies | 0 | 100 | 200 | 300 | 700 |
Cost of Option S (in Rands) | 0 | 200 | 400 | 600 | 1400 |
Cost of Option M (in Rands) | 500 | 550 | 600 | 650 | 850 |
Cost of Option XL (in Rands) | 200 | 350 | 500 | 650 | 1050 |
Use the above information to answer the following questions.
2.1.1 Name the independent variable in TABLE 3. (2)
2.1.2 Graphs to represent the relationship between the copies printed and the total cost of Option S and Option XL are drawn. On the same system of axes sketch the graph representing copies and total cost for Option M. (3)
2.1.3 Use the graph to determine the number of copies at break-even point for Options S and XL. (2)
2.1.4 Use the graph to determine the difference in cost of printing 600 copies between Option S and Option M. (3)
2.2
The financial statement for the years ending June 2018 and June 2109 for MATC municipality is shown TABLE 4 below. The statement shows some of the departments. | |||||
TABLE 4: | STATEMENT FOR YEARS ENDING JUNE 2018 AND JUNE 2019 FOR MATC MUNICIPALITY | ||||
2018 | 2019 | ||||
Departments | Income in Rands | Expenditure in Rands | Income in Rands | Expenditure in Rands | Surplus OR Deficit in Rands |
Public Works | 6 403 835 | 7 044 218 | 6 985 561 | 8 382 673 | (1 397 112) |
Statistics | 2 461 729 | 3 200 247 | 2 177 786 | 1 959 750 | (2 118 036) |
Education | 21 476 614 | 21 519 059 | 22 993 225 | 24 765 440 | (1 772 215) |
Agriculture | 49 137 536 | 50 342 890 | 52 307 560 | 51 200 460 | 1 107 100 |
Health | 38 496 020 | 39 785 320 | 42 645 344 | 63 960 168 | (21 314 824) |
Energy | 7 512 788 | --- | 8 145 563 | 8 145 975 | (412) |
Use the information in TABLE 4 to answer the following questions.
2.2.1 The expenditure for the year 2018 is 368 182 more than 2018 income. Calculate the percentage difference (rounded off to the nearest whole percentage) in the expenditure of Department of Energy from 2018 to 2019.
Use the following formula:
% difference = ??????????? ????−??????????? ???? × ???% (5)
??????????? ????
2.2.2 Determine the projected income in 2020 from Department of Public Works if it is expected to increase by 18,5% based on 2019 income. (4)
2.2.3 Calculate the probability (expressed as a simplified fraction) of randomly selecting a department that had income less than 25 million in 2018. (3)
2.3
Mr John is to deposit R5 000 in his bank account. |
John claims that the difference of depositing R5 000 at an ATM and at a branch is R18,20.
Verify this statement. (5)
[27]
QUESTION 3
Study the information on the number of special needs schools and number of designated full-service schools from the 9 provinces, and answer the questions that follow.
PROVINCE | NUMBER OF SPECIAL NEEDS SCHOOLS | NUMBER OF DESIGNATED FULL- SERVICE SCHOOLS |
Eastern Cape | 43 | 30 |
Free State | 21 | 175 |
Gauteng | 149 | 19 |
KwaZulu -Natal | 72 | E |
Limpopo | 34 | 17 |
Mpumalanga | 20 | 140 |
North West | 32 | 182 |
Northern Cape | 11 | 12 |
Western Cape | 83 | 40 |
TOTAL | 675 |
[Adapted from www.iol.co.za]
3.1 Write down the total number of special needs schools in South Africa. (2)
3.2 Arrange the number of special needs schools in descending order. (2)
3.3 Write down the simplified ratio of the number of special schools in Mpumalanga with the number of designated full-service schools in Western Cape. (3)
3.4 Calculate the value of E, the number of designated full-service schools in KwaZulu-Natal. (2)
3.5 Express the total number of schools in North West as a percentage of total number of schools in South Africa. (4)
3.6 Determine the province that lies in the median position of the special needs school. (2)
[15]
QUESTION 4
The data for the number of learners at Vula High School in 2018, is represented in the table below. Some of the values have been omitted.
TABLE 5: NUMBER OF LEARNERS AT VULA HIGH SCHOOL
Grades | 8 | 9 | 10 | 11 | 12 | Total |
Females | 121 | 103 | 76 | B | 42 | 406 |
Males | A | 95 | 78 | 59 | 33 | … |
Total | 222 | … | 154 | 123 | 75 | C |
4.1 Calculate the missing values A, B and C respectively, that are represented in the TABLE 5. (5)
4.2 Describe the trend in the number of male learners from Grade 8 to Grade 12 and give a possible reason for your answer. (4)
4.3 In this school, the teacher-learner ratio is 1 : 35. The SGB (School Governing Body) claims that the school is supposed to have 21 teachers. Verify, with the necessary calculations, whether their claim is valid or not. (4)
4.4 Determine the probability as a percentage of randomly selecting a female learner in this school that is either in Grade 8 or Grade 9. (3)
4.5 The school is a No Fee school where the learners receive one meal per day.
NOTE:
- The government is paying R3,18 per learner per day for nutrition
- Term 1 has 51 days
- Term 2 is 5 days shorter than term 1
The school principal claims that if the number of learners in 2019 increase by 3% more than what they were in 2018, the total school nutrition amount for term 1 and term 2 will be more than R245 000. Verify, with the necessary calculations, whether the principal’s claim is valid or not. (7)
[23]
QUESTION 5
5.1 Inako, is a 63-year-old educator at Vula High School. She earns R43 500 a month. She contributes 7,5 % of her gross salary towards her pension fund every month. She has a medical aid and has also medical cover for the following people:
- Her 83-year-old mother, Nondwe
- Her 65-year-old husband, Ngqika
- Two grandchildren, Alakhe and Ukuye
Taxable income (R) | Rates of tax (R) |
1 – 216 200 | 18% of taxable income |
216 201 – 337 800 | 38 916 + 26% of taxable income above 216 200 |
337 801 – 467 500 | 70 532 + 31% of taxable income above 337 800 |
467 501 – 613 600 | 110 739 + 36% of taxable income above 467 500 |
613 601 – 782 200 | 163 335 + 39% of taxable income 613 600 |
782 201 – 1 656 600 | 229 089 +41% of taxable income above 782 200 |
1 656 601 and above | 587 593 + 45% of taxable income above 1 656 600 |
REBATES | |
AGE | TAX YEAR – 2022 |
Primary – less than 65 | R15 714 |
65 and older | R8 613 |
75 and older | R2 871 |
Medical Tax Credit | Tax Year – 2022 |
Taxpayer | R332 |
First Dependent | R332 |
Each Additional Dependent | R224 |
[Source: www.sars.gov.za]
5.1.1 Calculate Inako’s annual income. (2)
5.1.2 Inako calculated her monthly tax and said she will contribute R1 790. Verify this statement. (6)
5.2
Mathematical Literacy P1 of the Trial Examination in 2020 was marked out of 150 marks. Learners in a grade 12B class scored the marks listed below. 101; 107; 121; 98; 100; 114; 103; 101; 110; 105; 102; 99; 95; 111; 115 |
Use the above information to answer the questions that follow.
5.2.1 Determine the median. (2)
5.2.2 Calculate the interquartile range (IQR). (5)
[15]
TOTAL: 100
ANSWER SHEET:
QUESTION 2.1.3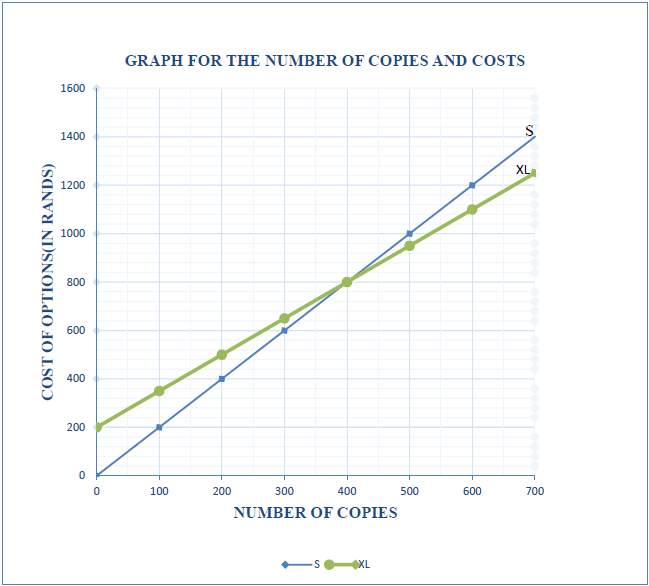
Physical Sciences Paper 2 Memorandum - Grade 12 June 2021 Exemplars
MEMORANDUM
QUESTION 1
1.1 D √√ (2)
1.2 D √√ (2)
1.3 A √√ (2)
1.4 C √√ (2)
1.5 C √√ (2)
1.6 D √√ (2)
1.7 B √√ (2)
1.8 B √√ (2)
1.9 B √√ (2)
1.10 C √√ (2) [20]
QUESTION 2
2.1
2.1.1 Homologous series √ (1)
2.1.2 Unsaturated. √
Contains a triple bond √/multiple bonds (2)
2.1.3 C5H9 √ (1)
2.1.4 5- ethlyl √ -2-methyl √ hex-3-yne √ OR 5-ethlyl-2-methyl-3-hexyne
Marking Criteria
- Hexyne √
- Side chains (ethyl and methyl) √
- Whole name correct √ (3)
2.2.1 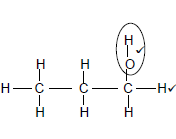
Marking criteria √
- Functional group correct (1/2)
- Whole structure correct (2/2) (2)
2.2.2 (Mild) heat √ in a water bath √ (2)
2.2.3 Esterification/ Condensation √ (1)
2.2.4 H2SO4 √ (1)
2.2.5 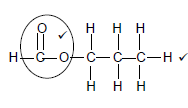
Marking criteria √
- Functional group √ correct (1/2)
- Whole structure correct (2/2) (2)
2.3
2.3.1 Compounds with the same molecular formula. √ but different structural formula. √ (2)
2.3.2 The C atom bonded to Br is bonded to one other C atom √√ OR The C atom bonded to Br is bonded to two hydrogen atoms (2)
2.3.3 1-bromo-2-methylpropane √√√
Marking Criteria
- Propane √
- (bromo and methyl) √
- Whole name correct √ (3)
[22]
QUESTION 3
3.1 The temperature at which the vapour pressure of a liquid equals the atmospheric pressure. √√ (2)
3.2 A √ Compound A has the lowest boiling point. √ (2)
3.3.1 Molar mass/ Molecular size/ Surface area √ (1)
3.3.2 Hydrogen bond √ (1)
3.4
- The molar mass/Molecular size/ surface area of the compounds increases from top to bottom in the table. √
- The compounds have London forces and (Hydrogen bonds) √
- The strength of London forces increases with an increase in molar mass/molecular size/surface area. √
- More energy is needed to overcome the intermolecular forces √ (4)
3.5.1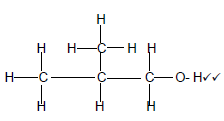
Marking criteria
- 3 Carbon atoms in longest chain with correct functional group (2)
3.5.2 B √ It has the same molecular formula √ (2)
3.5.3 Lower than √ (1)
3.5.4
- 2-methylpropan-1-ol has a smaller surface area than butan-1-ol. √
- Both compounds have London forces and (hydrogen bonds) √
- 2-methylpropan-1-ol have weaker London forces than butan-1-ol √
- Less energy is needed to overcome the intermolecular forces in 2-methylpropan-1-ol √
OR
- Butan-1-ol has a larger surface area than 2-methylpropan-1-ol √
- Both compounds have London forces and (hydrogen bonds) √
- Butan-1-ol have stronger Londonforces than 2-methylpropan-1-ol √
- More energy is needed to overcome the intermolecular forces in butan-1-ol √ (3)
3.6
- Methanoic acid and propan-1-ol have both Hydrogen bond and (London forces) √
- Methanoic acid have two sites for hydrogen bonds while propan-1-ol have only one site for hydrogen bonds. √
- Methanoic acid has stronger intermolecular forces than propan-1-ol √
- More energy is needed to overcome the intermolecular forces in methanoic acid. √
OR
- Methanoic acid and propan-1-ol have both Hydrogen bond and (London forces) √
- Methanoic acid have two sites for hydrogen bonds while propan-1-ol have only one site for hydrogen bonds. √
- Propan-1-ol has weaker intermolecular forces than methanoic acid √
- Less energy is needed to overcome the intermolecular forces in propan-1-ol. √ (4)
[22]
QUESTION 4
4.1 Process of breaking down long chain hydrocarbons √/alkanes into smaller more useful chains √ (2)
4.2
4.2.1 C4H10 √√ (2)
4.2.2 HIGH TEMPERATURE √ OR HIGH PRESSURE (1)
4.3
4.3.1 Substitution √ (1)
4.3.2 Elimination √ (1)
4.4 Hydrogenation √ (1)
4.5
4.5.1 Br2/Bromine √ (1)
4.5.2 Pt/Ni/Pd/Platinum/Nickel/Palladium √ (1)
4.6 CH3CH2CH2CHBr √√+ KOH → CH3CH = CHCH3 √√ + KBr + H2O
Marking criteria
- Organic reactant √√
- Organic product √√
- ALL Inorganic reagents correct √ (KOH, KBr and H2O) (5)
[15]
QUESTION 5
5.1 Change in concentration (of reactant/products) per unit time √√
OR
Amount/Volume/Mass of reactant/product used/formed per unit time (2)
5.2 RELEASED √
ΔH < 0 √/Energy of products is less than the energy of reactants/
Reaction exothermic (2)
5.3
5.3.1 INCREASES √ (1)
5.3.2 NO EFFECT √ (1)
5.4
5.4.1 After 120 s √ (1)
5.4.2 Concentration (of HCℓ) √ Surface area (of Zinc) √ OR temperature (2)
5.5
5.5.1 Rate / Tempo = Δv/Δt= 300 -0√ /120 – 0 √= 2,50 cm3∙s-1 √ (3)
5.5.2 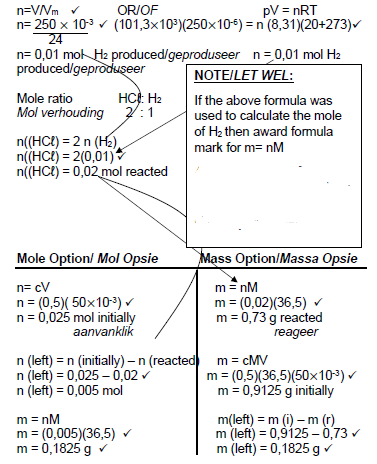 (7)
(7)
5.6
5.6.1 Catalyst √ OR Increases reaction rate (1)
5.6.2
- Catalyst lowers activation energy/provides an alternative path of lower activation energy √
- More particles have sufficient Ek OR more particles have Ek>Ea √
- More effective collisions per unit time/Frequency of effective collisions increase √√ (4)
[24]
QUESTION 6
6.1 Reaction in which products can be converted back to reactants √√ (2 or 0) (2)
6.2
6.2.1 Decreases √ (1)
6.2.2 Increases √(1)
6.3
- (When the temperature is decreased) the exothermic reaction is favoured √
- Forward reaction is favoured √ (2)
6.4 CALCULATION USING MOLES
Marking guideline
- Formula n=m/M
- Substitution of 28 g∙mol-1
- Use of ratio N2:H2:NH3
- Equilibrium amounts of N2 and H2 formed
- Division n equilibrium of N2, H2 and NH3 by 2
- Correct Kc expression
- Substitution into Kc expression
- Final answer
n = m/M √
= 7,84/28 √
= 0,28 mol
N2 + 3 H2 ⇋ 2 NH3
ni (mol) 0,28 0,6 0
Δn (mol) 0,06 0,18 0,12 Ratio √
ne (mol) 0,22 0,42 √ 0,12
ce 0,22/2 0,42/2 0,12/2 Division by 2 √
(mol∙dm-3) =0,11 0,21 0,06
Kc = [NH3]2/[N2].[H2]3 √
= 0,062/(0,11 x 0,213) √
= 3,53 √
CALCULATION USING CONCENTRATION
Marking guidelines
- Formula c=m/MV or c=n/v
- Substitution into c=m/MV or c=n/V
- Dividing by 2 for all concentration
- Use of ratio N2:H2:NH3
- Equilibrium concentrations of N2, H2 and NH3
- Correct Kc expression
- Substitution into Kc expression
- Final answer
- (Any one)
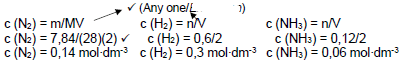
(dividing by) √
N2 + 3 H2 → 2 NH3 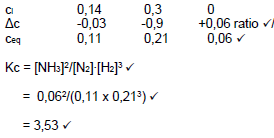 (8)
(8)
6.5 As pressure increases percentage yield increases. √√ (2)
6.6 MOLE OPTION
| Ratio N2 : H2 | Ratio N2 : H2 |
| 1 : 3 | 1 : 3 |
| n(H2) = 3 (0,28) √ n(H2) = 0,84 mol of H2 needed only 0,6 mol of H2 is available | n(N2) = 1/3 (0,6) n(N2) = 0,2 mol of N2 needed 0,28 mol of N2 is available |
0,84 mol van H2 word benodig 0,2 mol N2 word benodig
∴ H2 is the limiting reagent √ ∴ H2 is the limiting reagent
Theoretical yield/Teoretiese opbrengs = 0,6 x 2/3 = 0,4 mol √
% Yield = actual yield /theoretical yield × 100 %
= 0,12/0,4 x 100 √
= 30%
Pressure = 100 (atmospheres) √
CONCENTRATION OPTION
- V is constant
- Concentration ratio N2 : H2 Concentration ratio N2 : H2
1: 3 1 : 3
c(H2) = 3 (0,14) √ c(N2) = 1/3 (0,3)
c(H2) = 0,42 mol∙dm-3 of H2 required c(N2) = 0,1 mol∙dm-3
only 0,3 mol∙dm-3 is available 0,14 mol∙dm-3 is available
∴ H2 is the limiting reagent √
Theoretical yield = 0,3×2/3 √= 0,2 mol∙dm-3
- % yield = actual yield /theoretical yield ×100 %
- % yield = 0,06/0,2 ×100 % √
- % yield = 30 %
- Pressure 100 (atmosphere) √ (5)
[21]
QUESTION 7
7.1
7.1.1 Reaction of a salt with water √√ (2)
7.1.2 (Excess) Hydroxide/OH- ions are formed √
Hydroxide/ OH- is basic/alkaline √ (2)
7.1.3 H2O √ and HCO3- √ (2)
7.1.4 HCO3- can accept a proton (H+) (to form H2CO3) √
HCO3- can donate a proton (H+) (to form CO32-) √ (2)
7.2
7.2.1 Acid is a proton donor √√ (2)
7.2.2
- pH = - log [H3O+] √
1 = - log [H3O+] √
[H3O+] = 0,1 mol∙dm -3 √
[X] = 2 [H3O+]
[X] = 2(0,1)
[X] = 0,2 mol∙dm -3 √ (4)
7.2.3 It is a solution of known concentration √√ (2)
7.2.4 Bromothymol blue √ Acid X is a strong acid. KOH is a strong base. √
There is no hydrolysis of the salt produced, therefore the equivalence point of the titration would be within the range of indicator. √ (3)
7.2.5 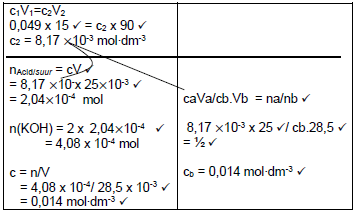 (7)
(7)
[26]
TOTAL: 150
Physical Sciences Paper 2 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
- Write your name and surname in the appropriate space on the ANSWER BOOK.
- This question paper consists of SEVEN questions. Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page in the ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Leave ONE line between two subquestions, for example between QUESTION 2.1 and QUESTION 2.2.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- You are advised to use the attached DATA SHEETS.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, et cetera where required.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1–1.10) in the ANSWER BOOK, for example 1.11 E.
1.1 The general formula for ALKANES is …
- CnH2n.
- CnH2n-1.
- CnH2n-2.
- CnH2n+2. (2)
1.2 The following graph shows the relationship between the number of carbon atoms in a straight chain molecules of alkanes, alcohols and aldehydes.
Curves P, Q and R is obtained.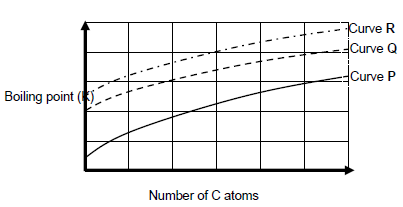
Which ONE of the following CORRECTLY describes the homologous series against the curve?
Curve P | Curve Q | Curve R | ||
A | Alcohols | Aldehydes | Alkanes | |
B | Aldehydes | Alcohols | Alkanes | |
C | Alcohols | Alkanes | Aldehyde | |
D | Alkanes | Aldehydes | Alcohols |
(2)
1.3 An alkene reacts with an EXCESS amount of water in the presence of an acid catalyst to produce compound P as shown in the equation below.
ALKENE + H2O → compound P
Compound P is a(n) …
- alcohol.
- alkane.
- haloalkane.
- carboxylic acid. (2)
1.4 Activation energy of a chemical reaction is defined as:
- Net energy released
- Net energy absorbed
- Minimum energy needed to start the reaction
- Maximum energy needed to start the reaction (2)
1.5 Consider the potential energy diagram for a reversible hypothetical reaction represented by the balanced equation below.
X2(g) ⇌ 2X(g)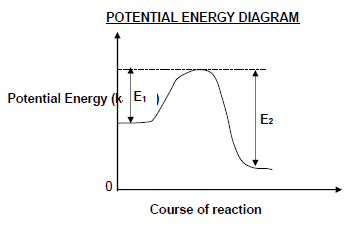
E1 and E2 are the activation energies for the forward and reverse reactions respectively. The difference (E2 – E1) is equal to …
- energy of the product.
- ΔH for the forward reaction.
- ΔH for the reverse reaction.
- energy of the activated complex. (2)
1.6 A chemical reaction reaches chemical equilibrium in a closed system. At equilibrium concentration of products and reactants remains constant because the rate of the forward reaction is …
- zero.
- higher than the rate of the reverse reaction.
- lower than the rate of the reverse reaction.
- equal to the rate of the reverse reaction. (2)
1.7 Consider the following reaction at equilibrium in a closed system.
Cu(H2O)62+ (aq) + 4 Cℓ- (aq) ⇋ CuCℓ42- (aq) + 6 H2O (ℓ) ΔH > 0
BLUE GREEN
Which ONE of the following changes to the equilibrium mixture above will ensure a COLOUR change from GREEN to BLUE?
- Increase in pressure
- Addition of silver nitrate
- Increase in temperature
- Addition of hydrochloric acid (2)
1.8 The endpoint in a titration is the exact point where …
- neutralisation occurs.
- the indicator changes colour.
- equal masses of base and acid have reacted.
- equal number of moles of acid and base have reacted. (2)
1.9 In the table below the ionisation constant values for bases, Kb at 25 °C are given.
Which ONE of the following bases is the STRONGEST?
BASE | Kb at 25 °C | |
A | SO42- | 8,3 x 10 -13 |
B | PO43- | 5,9 x 10-3 |
C | HCO3- | 2,4 x 10 -8 |
D | CH3COO- | 5,6 x 10 -10 |
(2)
1.10 Water undergoes auto-ionisation according to the balanced equation:
H2O(ℓ) + H2O(ℓ) ⇋ H3O+ (aq) + OH- (aq) ΔH > 0
The ionisation constant Kw for water is 1,00 x 10 -14 at 25 °C
Which ONE of the following is TRUE when the temperature of water in a beaker is increased from 25 °C to 30 °C?
- Kw remains the same and the water becomes acidic
- Kw remains the same and the water remains neutral
- Kw increases and the water remains neutral
- Kw decreases and the water remains neutral (2)
[20]
QUESTION 2 (Start on a new page.)
2.1 The compound P, shown below, belongs to alkynes which is a group of organic compounds with the same general formula and functional group.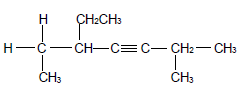
2.1.1 Write down a general term for the underlined phrase. (1)
2.1.2 Is compound P a SATURATED or UNSATURATED compound? Give a reason for the answer. (2)
For compound P write down the:
2.1.3 Empirical formula (1)
2.1.4 IUPAC name (3)
2.2 Consider compounds A and B given below.
- propan-1-ol
- HCOOH
2.2.1 Write down the STRUCTURAL formula of compound A. (2)
Compounds A and B are heated together in the presence of a catalyst in a test tube to produce an ESTER.
2.2.2 Describe how the mixture of A and B in the test tube is heated. (2)
For the reaction between compounds A and B write down the:
2.2.3 Name of the reaction taking place (1)
2.2.4 Formula of the catalyst used (1)
2.2.5 STRUCTURAL formula of the ester that is produced (2)
2.3 Haloalkanes, compounds C, D and E are structural isomers.
Compounds C and D are shown below and compound E is not shown:
C: CH3CH2CH2CH2Br D: (CH3)3CBr
2.3.1 Define the term structural isomer. (2)
2.3.2 Give a reason why compound C is classified as a PRIMARY haloalkane. (2)
2.3.3 Write down the IUPAC name of compound E, the POSITIONAL isomer of compound D. (3)
[22]
QUESTION 3 (Start on a new page.)
A group of learners investigated the effect of intermolecular forces on the boiling points of compounds.
They tabulated their results below:
Compounds Boiling point (°C) A Propan-1-ol 97 B Butan-1-ol 117,7 C Pentan-1-ol 138 |
3.1 Define the term boiling point. (2)
3.2 Which compound (A, B or C) will have the highest vapour pressure at a given temperature? Refer to the data in the table to explain the answer. (2)
3.3 For this investigation, write down the:
3.3.1 Independent variable (1)
3.3.2 Controlled variable (1)
3.4 Explain the trend in boiling point in the table above by referring to the MOLECULAR STRUCTURE, INTERMOLECULAR FORCES and ENERGY involved. (4)
3.5 The compound, 2-methylpropan-1-ol is a CHAIN ISOMER of one of the compounds in table.
3.5.1 Write down the structural formula for 2-methylpropan-1-ol. (2)
3.5.2 Which compound (A, B, or C) in the table above is a CHAIN ISOMER of 2-methylpropan-1-ol? Give a reason for the answer. (2)
3.5.3 How will the boiling point of 2-methylpropan-1-ol compare to the isomer named in QUESTION 3.5.2? Write only HIGHER THAN, LOWER THAN or EQUAL TO. (1)
3.5.4 Explain the answer to QUESTION 3.5.3 by referring to the MOLECULAR STRUCTURE, INTERMOLECULAR FORCES and ENERGY involved. (3)
3.6 Methanoic acid is a smaller compound than propan-1-ol. The boiling point of methanoic acid is HIGHER than propan-1-ol. Fully explain why the boiling point of methanoic acid is higher than propan-1-ol. Refer to the TYPE OF INTERMOLECULAR FORCES and energy involved. (4)
[22]
QUESTION 4 (Start on a new page.)
Hexane undergoes thermal cracking according to the balanced equation below.
C6H14 → Alkane X + C2H4
4.1 Define cracking. (2)
4.2 Write down the:
4.2.1 Molecular formula of alkane X (2)
4.2.2 One reaction condition (1)
The alkane X, produced in the cracking reaction above, is used to produce other organic compounds as shown in the flow diagram below.
The numbers I, II and III represent organic reactions.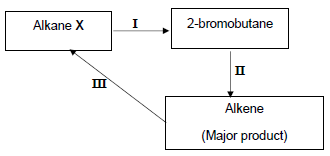
4.3 Write down the TYPE of reaction represented by:
4.3.1 I (1)
4.3.2 II (1)
4.4 Write down the NAME of the type of addition reaction represented by reaction III. (1)
4.5 Write down the NAME or FORMULA of the:
4.5.1 Inorganic reactant used in reaction I (1)
4.5.2 Catalyst used in reaction III (1)
4.6 Write down a balanced equation using CONDENSED structural formulae of organic reagents for reaction II. (5)
[15]
QUESTION 5 (Start on a new page.)
A group of learners conduct experiments to investigate a factor that affects the rate of reactions.
In the experiments, the learners use the reaction between zinc granules and EXCESS hydrochloric acid of concentration 0,5 mol∙dm-3 at 20 °C as shown below:
Experiment A: Zn (s) + 2 HCℓ (aq) → ZnCℓ2 (aq) + H2 (g) ΔH < 0
5.1 Define reaction rate. (2)
5.2 Is net energy ABSORBED or RELEASED during the reaction? Give a reason for the answer. (2)
5.3 How will the rate of reaction in experiment A be affected by the following changes? Choose from INCREASES, DECREASES or NO EFFECT.
5.3.1 Using H2SO4 solution of concentration 0,5 mol∙dm-3 in place of the HCℓ. (1)
5.3.2 Pressure is increased. (1)
5.4 In experiment A, 50 cm3 of hydrochloric acid (HCℓ) solution of concentration 0,5 mol∙dm-3 reacts with 7,15 g of zinc (Zn) granules.
The volume gas formed versus time for the reaction in experiment A is shown below.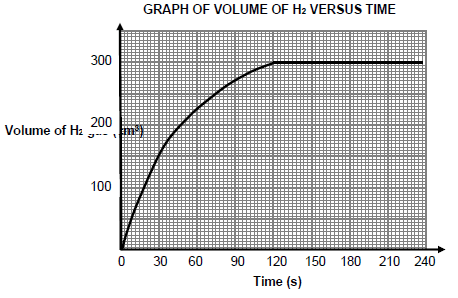
5.4.1 How many seconds did the reaction take to reach completion? (1) It is observed that the rate of reaction is HIGHEST during the interval 0 to 30 s.
5.4.2 Write down TWO factors that influence reaction rate that explains this observation. (2)
5.5 Calculate the:
5.5.1 Average rate of reaction (in cm3∙s-1) for the first 120 s (3)
5.5.2 Mass of the EXCESS reactant remaining in the flask if the molar volume of hydrogen gas at 20 °C is 24 dm3∙mol-1 (7)
5.6 In experiment B, the reaction in experiment A is repeated under the same conditions, but copper is also added to the reaction mixture.
Cu
Experiment B: Zn (s) + HCℓ (aq) → ZnCℓ2 (aq) + H2 (g)
The Maxwell-Boltzman distribution curve for the reaction in experiment A and in experiment B is shown below: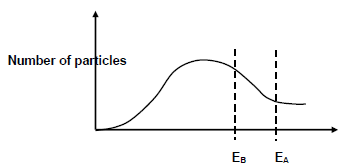
EA and EB represent the activation energy for the reaction in experiments A and B respectively.
5.6.1 What is the function of copper in experiment B? (1)
5.6.2 Explain how the addition of copper in reaction B affects the rate of reaction by referring to the collision theory. (4)
[24]
QUESTION 6 (Start on a new page.)
The reversible reaction given below reaches equilibrium at 350 °C in a closed container.
N2(g) + 3 H2(g) ⇋ 2 NH3(g) ΔH < 0
6.1 Define the term reversible reaction. (2)
6.2 The temperature of the equilibrium mixture is decreased. How will the decrease in temperature affect the following? Choose from INCREASES, DECREASES or REMAINS CONSTANT.
6.2.1 Rate of the forward reaction (1)
6.2.2 Number of moles of NH3 at equilibrium (1)
6.3 Explain the answer to QUESTION 6.2.2 above by referring to Le Chatelier’s principle. (2)
6.4 The reaction is started by placing 7,84 grams of N2 and 0,6 moles of H2 in an empty flask which is then sealed. When equilibrium is reached at 350 °C the amount of NH3 present is 0,12 moles. The volume of the container is 2 dm3. Calculate the value of the equilibrium constant at 350 °C. (8)
The graph shown below shows the percentage yield of NH3 at 350 °C at different pressure values.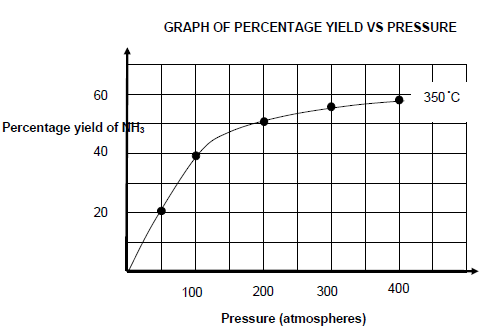
6.5 Write down a CONCLUSION that can be drawn from the graph about the relationship between percentage yield of NH3 and pressure at constant temperature. (2)
6.6 Use information from QUESTION 6.4 and the graph to determine the pressure at which the reaction reached equilibrium. (5)
[21]
QUESTION 7 (Start on a new page.)
7.1 Sodium carbonate ionises in water into sodium ions (Na+) and carbonate ions (CO32-). Carbonate ions in solution undergo hydrolysis according to the balanced equation:
CO32- (aq) + H2O (ℓ) ⇋ HCO3- (aq) + OH- (aq)
7.1.1 Define hydrolysis. (2)
7.1.2 Give a reason why a solution of sodium carbonate in water is alkaline by referring to substance(s) in the equation above. (2)
7.1.3 Write down the FORMULAE of the TWO acids in the equation. (2)
7.1.4 Give a reason why HCO3- can act as an ampholyte. (2)
7.2 A solution of a strong diprotic acid X has pH = 1.
7.2.1 Define an acid according to the Lowry-Bronsted theory. (2)
7.2.2 Calculate the concentration of acid X. (4) A solution of acid X of concentration 0,049 mol.dm-3 is diluted by adding 15 cm3 of the acid to water to produce 90 cm3 of a dilute standard solution.
7.2.3 Explain the meaning of the term standard solution. (2)
The DILUTE solution of acid X is titrated with a solution of potassium hydroxide.
The following list of indicators are available for the titration.
Indicator | pH-range |
Methyl orange | 3,1 – 4,4 |
Bromothymol blue | 6,0 – 7,6 |
Phenolphthalein | 8,3 – 10,0 |
7.2.4 Which ONE of the indicators is the most suitable for this titration? Explain the answer. (3)
During the titration 25 cm3 of the DILUTE acid X solution neutralises exactly 28,5 cm3 of a potassium hydroxide solution.
7.2.5 Calculate the concentration of the potassium hydroxide solution. (7)
[26]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES GRADE 12
PAPER 2 (CHEMISTRY)
TABLE 1: PHYSICAL CONSTANTS
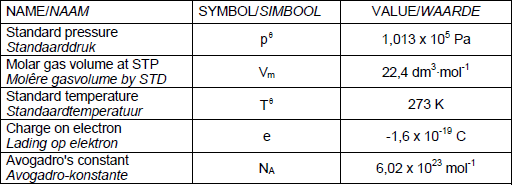
TABLE 2: FORMULAE 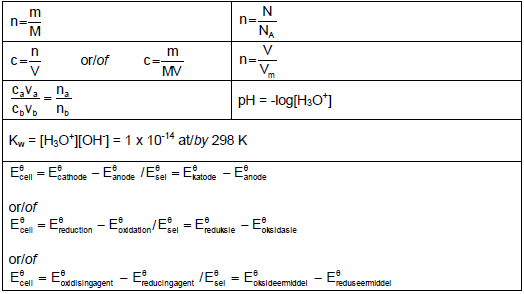
PERIODIC TABLE
TABLE 4A: STANDARD REDUCTION POTENTIALS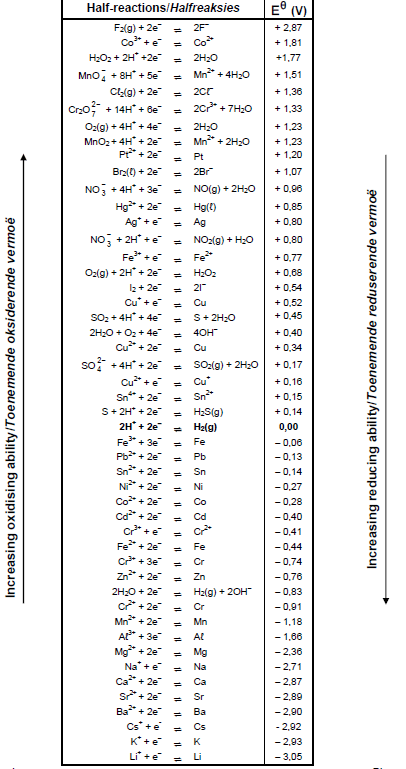
TABLE 4B: STANDARD REDUCTION POTENTIALS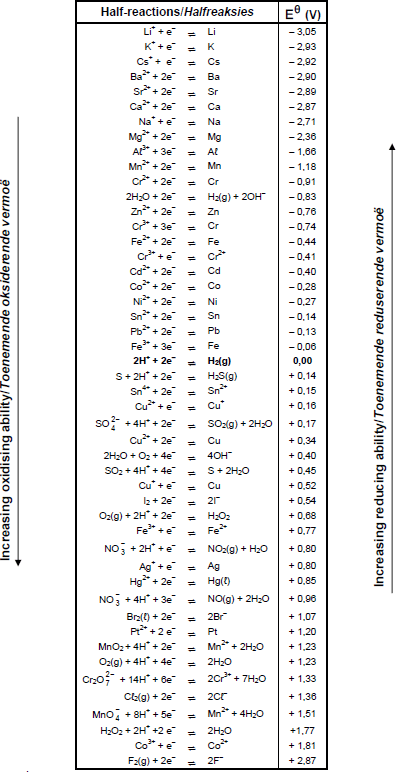
Physical Sciences Paper 1 Memorandum - Grade 12 June 2021 Exemplars
MEMORANDUM
QUESTION 1
1.1 B √√ (2)
1.2 C √√ (2)
1.3 C √√ (2)
1.4 D √√ (2)
1.5 A √√ (2)
1.6 C √√ (2)
1.7 B √√ (2)
1.8 A √√ (2)
1.9 D √√ (2)
1.10 B √√ (2) [20]
QUESTION 2
2.1 When object A exerts a force on object B, √ object B simultaneously exerts an oppositely directed force of the same magnitude on object A. √ (2)
2.2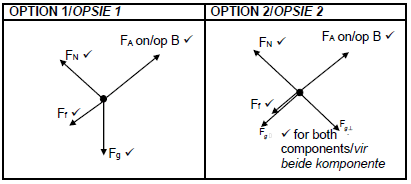 (4)
(4)
2.3 Data:
- MB = 25 kg
fB = 15 N
a = 1,5 m.s-2
FA on B = ?
FB on A = ?
Fnet = ma
FA on B + fB + Fg = ma √ Any one
FA on B + fB + mgSin35°= ma
FA on B + (- 15) + (- 25x9,8x0,574) √ = 25x1,5 √
FA on B – 155,63 = 37,50 FA on B = 193,13 N √
FB on A = - FA on B
FB on A = - 193,13 N
FB on A = 193,13 N √ down the slope √ (6)
2.4
- Fnet = ma
FNceba + FB on A + fA + Fg = ma √ Any one
FNceba + FB on A + fA + mgSin35°= ma
FNceba + (- 193,13) + (- 4,5) + (- 10x9,8x0,574) √ = 10x1,5 √
FNceba – 253,88 = 15
FNceba = 268,88 N √ (4)
[16]
QUESTION 3
3.1 When a net/resultant force acts on an object of mass m, the object accelerates in the direction of the net force. √ The accelereation is directly proportional to the net force and inversely proportional to the mass. √ (2)
3.2
- Fnet = ma
Fg + FN + FY = ma √ Any one
Fg + FN + Fa Sin40° = ma
Fg + (-623,3) + (-500Sin40°) = mx0 √
Fg - 623,3 – 321,39 = 0
Fg = 944,69 N
mg = 944,69 √
mx9,8 = 944,69 √
m = 96,40 kg √ (5)
3.3 For 96,4 kg box
- Fnet = ma
Fa Cos40° + f + T = ma
500 Cos40° + (-115) +(- T) √ = 96,4a √
383,02 – 115 – T = 96,4a
268,02 - T = 96,4a
T = 268,02 – 96,4a (1)
For 15 kg box
- Fnet = ma √ Any one
mg + T = ma
-15x9,8 + T√ = 15a √
-147 + T = 15a (Substitute)
-147 + (268,02 – 96,4a) = 15a
121,02 = 111,40a
a = 1,09 m.s-2 √ (7)
[14]
QUESTION 4
4.1 It (projectile) is an object upon which the only force acting is the force of gravity. √√
OR/OF
Projectile is an object that experiences only gravitational force. √√ (2)
4.2
OPTION 1 | |
(upwards positive) | (downwards positive) |
vf2 = vi2 + 2gΔy | vf2 = vi2 + 2gΔy |
OPTION 2 | |
(upwards positive) | (downwards positive) |
vf = vi + g∆t | vf = vi + g∆t |
(3)
4.3 The maximum height reached by ball A (Δymax) = 1,28 + 5 = 6,28 m
Maximum height reached by ball B is given by:
(upwards positive) | (downwards positive) |
vf2 = vi2 + 2gΔy 02 = 82 + 2 (-9,8) Δy ΔyB = 3,27 m Since ΔyB < Δymax OR 3,27 m < 6,28 m ∴ Ball B did not reach the maximum height. ü | vf2 = vi2 + 2gΔy 02 = (-8)2 + 2 (9,8) Δy Δy = -3,27 m ΔyB = 3,27 m, (upward) Since ΔyB < Δymax OR 3,27 m < 6,28 m ∴ Ball B did not reach the maximum height. |
(5)
4.4
(upwards positive) | (downwards positive) |
vf = vi + g∆t | vf = vi + g∆t 0 = (5) + (-9,8 ). ∆t vf = vi + g∆t |
(4)
4.5 (Upwards positive)
For ball A
vf = vi + g∆t √
vf = (5) + (-9,8 ). ∆t (1) √
For ball B
vf = vi + g∆t
vf = (8) + (-9,8 ). ∆t (2) √
Equating (1) and (2)/ Stel (1) gelyk aan (2):
Since ball A will be moving downwards then:
-(5 – 9,8.∆t) = 8 – 9,8.∆t √
19,6.∆t = 13
∆t = 0,66 s
∆t = 0,011min √ (5)
[19]
QUESTION 5
5.1 A system on which the net external forces acting is zero. √√ (2)
5.2 Let east be positive
- p = mv √
= 1 140 x 30 √
= 34 200 kg.m.s-1, (east) √ (3)
5.3
- Σpi = Σpf √
mvviv + mcvic = mvvfv +mcvfc
1 650 viv+ 1 140 x 30 √ = 1 650 x - 12 + 1 140x 10 √
1 650 viv = 11 400 – 34 200 – 19 800 viv = - 25,82
viv = 25,82 m.s-1 √, west √ (5)
5.4 Principle of conservation of linear momentum √
The total linear momentum of an isolated system remains constant (preserved). √√ (3)
5.5
- ∆p = m(vf - vi) √
∆p = 1 650 (-12 – (-25,82)) √
∆p = 22 803 kg.m.s-1 √ (3)
[16]
QUESTION 6
6.1 The net/resultant force acting on an object is equal to the rate of change in momentum of the object. √√ (2)
6.2
- Total Ek Before = Ek tree + Ek car
= ½m v2tree + ½m
= ½(m)(02) √ + ½(1 125)(25)2 √
= 351 562,5 J √ (4)
6.3 Impulse of the tree:
Let original direction be positive
- Fnet∆t (car) = m(vf - vi) √
= 1 125(-6 – 25) √
= - 34 875 N
Fnet∆t (car) = 34 875 N, backwards/terugwaarts
Fnet∆t (tree) = 34 875 N √, original direction of the car √ (4)
6.4
- Fnet (car) = m(vf - vi ) √
Δt
Fnet (car) = 1 125(-6 - 25) √
3,5
Fnet (car) = - 9 964 N
Fnet (car) = 9 964 N, backwards √ (3)
6.5 When the airbags deploy during collision, the contact time of the driver with the airbag increases. √ According to the equation Fnet∆t = ∆p, when contact time increases the net force experienced by the driver decreases. √ Then, the extent of injury is reduced. (2)
6.6 Decrease √
The final velocity will now be zero. √ Then, according to the equation:
∆p = m(vf – vi), it follows that ∆p will decrease. √ If ∆p decreases then Fnet decreases as they are directly proportional to each other. (4)
[19]
QUESTION 7
7.1
- F = Gm1m2 √
r2
F = (6,67 x10-11)( 3,4 x103 )( 5,98 x1024 ) √
(2,32 x106 )2 √
= 251 959,05
= 2,52 x 105 N √ (4)
7.2 Newton’s Law of Universal Gravitation √
Any two objects or particles in the universe attract each other with a force which is directly proportional to the product of their masses √ and inversely proportional to the square of the distance between their centres. √ (3)
7.3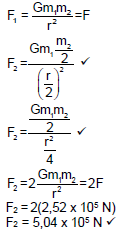 (3)
(3)
[10]
QUESTION 8
8.1
8.1.1 The net work done on an object is equal √ to the change in the kinetic energy of the object. √
OR
The amount of work done by a net force √ on an object is equal to the change in the object’s kinetic energy. √ (2)
8.1.2
OPTION 1 |
Wnet = WF1 + WF2 + W// + Wf |
OPTION 2 |
Fnet = F2 + F1 + Fg + f |
(4)
8.1.3 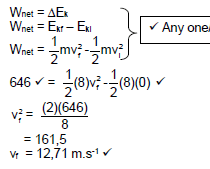 (4)
(4)
8.2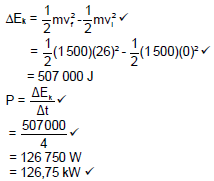 (5)
(5)
[15]
QUESTION 9
9.1
9.1.1 It is the apparent change in frequency (or pitch/wavelength) of the sound detected by a listener because the sound source and the listener have different velocities relative to the medium of sound propagation. √√
OR
An apparent change in observed/detected frequency (pitch/ wavelength) as a result of relative motion between a source and an observer. √√ (2)
9.1.2 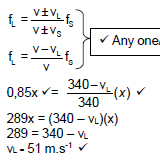 (4)
(4)
9.1.3 When the listener moves away from the source the sound waves that reach him have longer wavelength √ and a sound with a lower pitch is registered because of a lower frequency. √ (2)
9.1.4 It would be the same √√ (2)
9.1.5
- FL = 0,85fS
= 0,85 x 190 √
= 161,5 Hz √ (2)
9.2 To measure the velocity of blood flowing through blood vessels. √
To scan a fetus/foetus. √ (2)
[14]
QUESTION 10
10.1 The magnitude of the electrostatic force exerted by one point charge (Q) on another point charge (Q) is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance (r) between them. √√ (2)
10.2 East is positive
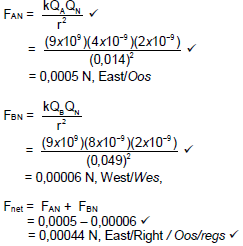 (5)
(5)
[7]
TOTAL: 150
Physical Sciences Paper 1 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
- This question paper consists of 10 questions.
- Answer ALL the questions.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Number the questions correctly according to the numbering system used in this question paper.
- You are advised to use the attached DATA SHEETS.
- The formulae and substitutions must be shown in ALL calculations.
- Give brief motivations, discussions, etc. where required.
- Round off your final numerical answers to a minimum of TWO decimal places.
- Start EACH question on a NEW page.
- All diagrams are not necessarily drawn according to scale.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Four possible options are provided as answers to the following questions. Choose the answer and write down (A–D) next to the question numbers (1.1–1.10) in your ANSWER BOOK, for example 1.11 D.
1.1 Safety belts in cars are designed to reduce the extent of injuries to passengers during accidents. Which ONE of Newton’s laws of motion best explains the tendency of a passenger’s body to move forward during a head-on collision?
- Law of Universal gravitation
- First Law
- Second Law
- Third Law (2)
1.2 An object of mass m rests on a flat table. If the action force of the Earth on this object is mg, which ONE of the statements given below best describes the reaction force?
- The table pushing up on the object with force mg
- The object pushing down on the table with force mg
- The object pulling upward on the Earth with force mg
- The table pushing down on the floor with force mg (2)
1.3 A constant net force, F, acts on a box which moves along a frictionless horizontal surface. Which ONE of the following quantities remains constant while the net force F acts on the box?
- Change in momentum
- Work done on the box
- Rate of change of velocity
- Change in gravitational potential energy (2)
1.4 A ball is dropped from a hot air balloon that is moving upwards at a constant velocity. Take UPWARDS as the POSITIVE direction. The correct velocity versus time graph for the motion of the ball and the balloon is: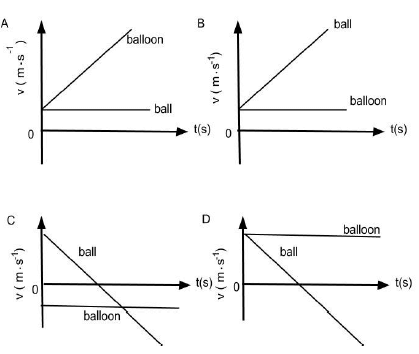 (2)
(2)
1.5 Two forces, each of magnitude 200 N, are simultaneously applied to a toolbox of mass 25 kg resting on a horizontal surface as shown in the diagram below. Ignore the effects of friction.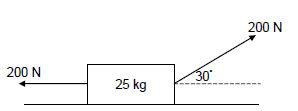
Work will be done by the net force on the toolbox because it will …
- accelerate to the left.
- accelerate to the right.
- be lifted off the surface.
- remain at rest. (2)
1.6 While a helicopter is moving vertically upwards with constant velocity, a camera is dropped from it. The camera lands on the ground after t1 seconds. The sketch graph below represents the velocity-time relationship of the camera’s motion. Downward direction is positive.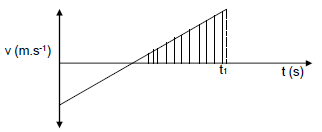
The shaded area under the graph represents the:
- Total distance the camera has travelled
- Speed with which the camera strikes the ground below
- Maximum height of the camera above the ground
- Magnitude of the displacement of the camera (2)
1.7 The work done by the car’s engine to increase its velocity from 0 to v is W. What work should be done by the engine to increase its velocity from v to 2v ?
- 4W
- 3W
- 2W
- W (2)
1.8 An ambulance moving at constant velocity, producing a sound, approaches a stationary listener, passes the listener and moves away. Which ONE of the following graphs best represents the change in observed frequency versus time?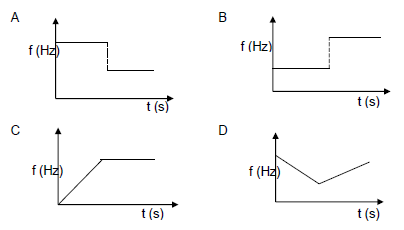 (2)
(2)
1.9 Two identical metal spheres, each carrying a charge Q, are at a distance r apart. Which ONE of the following pairs of changes, that are made simultaneously, will DOUBLE the electrostatic force that one charged sphere exerts on the other?
DISTANCE BETWEEN CENTRES OF SPHERES | MAGNITUDE OF CHARGES | |
A | Decrease distance to r | Reduce the charges on both spheres to Q |
B | Decrease distance to r | Double the charges on both spheres |
C | Decrease distance to r | Double the charges on both spheres |
D | Decrease distance to r | Reduce the charge on one sphere to Q |
(2)
1.10 Two objects experience an INELASTIC collision in an isolated system. Which ONE of the following combinations regarding the total momentum and total kinetic energy is correct?
Total momentum is … | Total kinetic energy is … | |
A | not conserved | conserved |
B | conserved | not conserved |
C | not conserved | not conserved |
D | conserved | conserved |
(2)
[20]
QUESTION 2 (Start on a NEW page.)
Two blocks, A and B, are placed on an inclined rough surface that makes an angle of 35° with the horizontal. Nceba is applying a force F on block A to push the system up the incline. Block B experiences a frictional force of 15 N.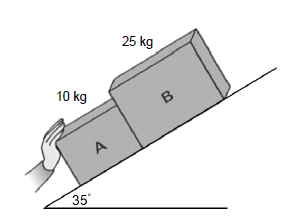
2.1 State Newton’s Third law of motion in words. (2)
2.2 Draw a labelled free-body diagram of all the forces acting on block B. (4)
2.3 If the system accelerates at 1,5 m.s-2 up the incline, calculate the force exerted by block B on block A. (6)
2.4 If block A experiences a frictional force of 4,5 N when the system was accelerating at 1,5 m.s-2, calculate the magnitude of the force applied by Nceba. (4)
[16]
QUESTION 3 (Start on a NEW page.)
Two boxes of mass m and 15 kg, are connected by a light inextensible string passing over a frictionless pulley. A force of 500 N is applied, at an angle of 40° to the horizontal, on the box of mass m as shown in the diagram below. The box of mass m experiences a frictional force of 115 N and a normal force, FN, of 623,3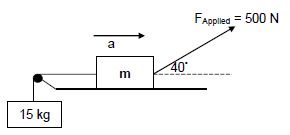
3.1 State Newton’s Second Law of motion in words. (2)
3.2 Calculate the value of m in the diagram above. (5)
3.3 Calculate the magnitude of the acceleration of the system as it moves towards the direction indicated on the diagram. (7)
[14]
QUESTION 4 (Start on a NEW page.)
Two balls A and B, are thrown simultaneously from different positions of the balcony overlooking the street. Ball A is thrown vertically upwards with a velocity of 5 m·s-1 from the top of a balcony and ball B is thrown vertically upwards with a velocity of 8 m.s-1 from the bottom of the balcony. Ignore effects of air resistance.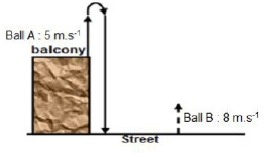
4.1 Define the term projectile. (2)
4.2 Calculate the magnitude of the displacement above the balcony of ball A. (3)
4.3 If the height of the balcony is 5 m, show by calculations whether or not ball B reached the maximum height reached by ball A. (5)
4.4 Calculate the speed at which ball B was moving when ball A reached its maximum height. (4)
4.5 At what time (in minutes) will the speed of the two balls be equal? (5)
[19]
QUESTION 5 (Start on a NEW page.)
A car of mass 1 140 kg, moving towards the east with a velocity of 30 m.s-1, collides with an oncoming delivery van of mass 1 650 kg. After collision, the van continues moving towards its original direction at 12 m.s-1 whilst the car moves at 10 m.s-1. The system is isolated.
5.1 What is meant by isolated system? (2)
5.2 Determine the magnitude of the initial momentum of the car. (3)
5.3 Calculate the velocity of the van before collision. (5)
5.4 Name and state the principle used to answer QUESTION 5.3. (3)
5.5 Calculate the change in momentum of the van. (3)
[16]
QUESTION 6 (Start on a NEW page.)
A car with a mass of 1 125 kg travelling at a constant velocity of 25 m.s-1 collided with a tree and rebounds with a velocity of 6 m.s-1.
The car was in contact with the tree for 3,5 s.
6.1 State Newton’s Second Law of motion in terms of momentum in words. (2)
6.2 Calculate the total initial kinetic energy of the system. (4)
6.3 Calculate the impulse of the tree during the collision. (4)
6.4 Calculate the average force experienced by the car. (3)
6.5 Discuss by using the principles of physics, how the airbags of the car reduce the extent of injuries suffered by the driver. (2)
6.6 If the car did not rebound from the tree but the time interval remained 3,5 s, how will the magnitude of the force exerted on the car be influenced? Write only INCREASE, DECREASE or REMAIN THE SAME. Explain the answer. (4)
[19]
QUESTION 7 (Start on a NEW page.)
A research satellite has a mass of 3,4 x 103 kg. It orbits the Earth at a distance of 2,32 x 106 m from the centre of the Earth, which has a mass of 5,98 x 1024 kg.
7.1 Calculate the gravitational force that the Earth exerts on the satellite. (4)
7.2 Name and state the law that is applicable to this situation. (3)
7.3 Another satellite of mass half that of the research satellite orbits at a distance half that of the research satellite from the centre of the Earth. Calculate the magnitude of the force of attraction between the Earth and this satellite. (3)
[10]
QUESTION 8 (Start on a NEW page.)
8.1 A crate of mass 8 kg was resting at point A on an inclined rough surface that makes an angle of 30° with the horizontal. Two forces F1 and F2, of 20 N and 100 N respectively, were simultaneously applied on the crate and it moved through a displacement of 20 m, as shown in the diagram below.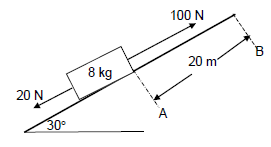
8.1.1 State the work-energy theorem in words. (2)
8.1.2 If the frictional force experienced by the crate is 8,5 N, calculate the net work done in moving the crate to point B. (4)
8.1.3 Use energy principles to calculate the velocity of the box as it passes point B. (4)
8.2 A race car with a mass of 1 500 kg can reach a speed of 26 m.s-1 from 0 m.s-1 in 4 s. Calculate the average power output of the car’s engine. (5)
[15]
QUESTION 9 (Start on a NEW page.)
9.1 A hospital staff member moves away from an ambulance. The siren of the ambulance produces a sound of an unkown frequency. The staff member hears 0,85 times the frequency of the siren as he moves away from the ambulance. The speed of sound in the air is 340 m.s-1.
9.1.1 Define Doppler effect. (2)
9.1.2 Calculate the velocity of the staff member as he moves away from the ambulance. (4)
9.1.3 Why is the frequency perceived by the listener moving away from the source lower than the actual frequency produced by the siren? (2)
9.1.4 If the staff member decided to get inside the ambulance, how would the frequency heard by the staff member compare, to that emitted by the ambulance? Write only GREATER THAN, SMALLER THAN or EQUAL TO. (2)
9.1.5 If the frequency of the source was 190 Hz, what will be the magnitude of the frequency registered by the staff member as he was moving away from the ambulance? (2)
9.2 Name TWO applications of the Doppler effect in Medical Science. (2)
[14]
QUESTION 10 (Start on a NEW page.)
The diagram below shows three point charges, A carrying a charge of -4 nC, B carrying a charge of +8 nC and N carrying a charge of +2 nC. These point charges are placed at distance apart from one another as shown in the diagram below.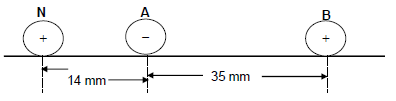
10.1 State Coulomb’s law in words. (2)
10.2 Calculate the magnitude and direction of the net force around point charge N due to the presence of both point charges A and B. (5)
[7]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES GRADE 12
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m•s-2 |
Universal gravitational constant | G | 6,67 × 10-11 N•m2•kg-2 |
Speed of light in a vacuum | c | 3,0 × 108 m•s-1 |
Planck's constant | h | 6,63 × 10-34 J•s |
Coulomb's constant | k | 9,0 × 109 N•m2•C-2 |
Charge on electron | e | -1,6 × 10-19 C |
Electron mass | me | 9,11 × 10-31 kg |
Mass of earth | M | 5,98 × 1024 kg |
Radius of earth | RE | 6,38 × 103 km |
TABLE 2: FORMULAE
MOTION
| vf = vi + aΔt | Δx = ViΔt + ½aΔt2 or Δy = ViΔt2 + ½aΔt2 |
Vf2 = Vi2 + 2aΔx or Vf2 = vi2 + 2aΔy | Δx = [Vi + Vf]Δt or Δy = [Vi + Vf]Δt |
FORCE
Fnet = ma | p= mv |
fsmax = µsN | fk = µkN |
FnetΔt = Δp | w =mg |
F = Gm1m2 | g = G M |
WORK, ENERGY AND POWER
W =FΔxcosθ | U= mgh or EP = mgh |
K = ½mv2 or Ek = ½mv2 | Wnet = ΔK or Wnet = ΔEk ΔK = Kf −Ki or ΔEk =Ekf − Eki |
Wnc= ΔK + ΔU or Wnc= ΔEk + ΔEp | P = W Δt |
Pav = Fv |
WAVES, SOUND AND LIGHT
v = f λ | T =1/f |
fl = v ± vl fs fl = v ± vl fb | E = hf or E = h c |
E = W0 + Ek where | |
ELECTROSTATICS
| F = kQ1Q2 r2 | E = KQ |
E = V | E = F |
V = W | n = Q |
ELECTRIC CIRCUITS
R = V | emf (ε) = I(R + r) |
RS = R1 + R2 + ....... | q = I Δt |
W = Vq | P= W |
ALTERNATING CURRENT
I rms = Imax | Paverage = VrmsIrms |
Technical Sciences Paper 2 Memorandum - Grade 12 June 2021 Exemplars
MEMORANDUM
QUESTION 1
1.1 D √√ (2)
1.2 C √√ (2)
1.3 B √√ (2)
1.4 A √√ (2)
1.5 B √√ (2) [10]
QUESTION 2
2.1 Combustion √ (1)
2.2 Structural isomers √ (1)
2.3 Polymers √ (1)
2.4 n-type (semiconductor) √ (1) [4]
QUESTION 3
3.1
3.1.1 An organic molecule is a molecule which contains carbon atoms. √√(2)
3.1.2 CnH2n √ (1)
3.1.3 Alcohols √ (1)
3.1.4 Hydroxyl group √ (1)
3.1.5 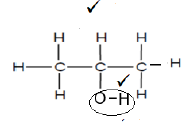 (2)
(2)
3.2
3.2.1 Esters: Dipole-dipole intermolecular forces √ (1)
Alcohols: Hydrogen bond √ (1)
3.2.2 Methanoic acid √ (1)
3.2.3 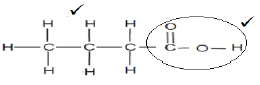 (2)
(2)
3.2.4 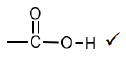 (1)
(1)
3.3
3.3.1 Same molecular formula, C5H12 (1)
3.3.2 Different chain length (1)
3.3.3 Alkanes (1)
3.4
3.4.1 Pentane (1)
3.4.2 2-methyl butane (2)
3.4.3 Pentane (1)
3.4.4 B (1)
3.4.5 B is branched; the more branches in the organic compound, the smaller the surface area. (2)
3.5
3.5.1 Plastics are synthetic materials derived from organic compounds.
3.5.2
USE | |
B | Food-packaging plastics |
C | Squeezable bottles |
E | Flexible water pipes |
(Any 2 x 1)(2) [27]
QUESTION 4
4.1 Vapour pressure is the pressure exerted by a vapour at equilibrium with its liquid in a closed system. √√ (2)
4.2 4.2.1 Dipole-dipole intermolecular forces √ (1)
4.2.2 Dipole-dipole intermolecular forces √ (1)
4.3 Viscosity of chlorohexane is HIGHER. √
Chlorohexane has stronger dipole-dipole intermolecular forces.
Pentane has weaker dispersion / London forces. √ (2)
4.4 Pentane √ - It has weak London forces. √ Less energy will be required to overcome intermolecular forces. √ (3)
4.5 London forces √√ (2)
[11]
QUESTION 5
5.1 Hydrocarbons are organic compounds that consist only of hydrogen and carbon atoms. √ (1)
5.2
5.2.1 CH4 + 2O2 √ CO2 + 2H2O √ √ bal (3)
5.2.2 Excess oxygen √ (1)
[5]
QUESTION 6
6.1 6.1.1 Hydrolysis √ (1)
6.1.2 Hydration √ (1)
6.1.3 Esterification √ (1)
6.2
6.2.1 Hexan-2-ol or 2-hexanol √ (1)
6.2.2 1-bromohexane √ (1)
6.2.3 Water √ (1)
6.3
6.3.1 Pt/Pd/Ni as a catalyst √ (1)
6.3.2 No water added, unreactive solvent, CHCl2, CCl4 √ (1)
6.4 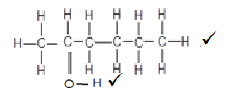 (2)
(2)
6.5
6.5.1 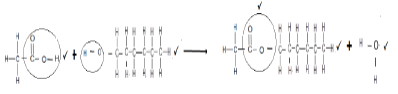 (4)
(4)
6.5.2 Ethyl hexanoate √ (1)
6.5.3 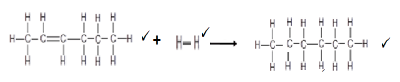 (3)
(3)
[18]
TOTAL: 75
Technical Sciences Paper 2 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
- This question paper consists of SEVEN questions. Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page in the ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Leave ONE line between two sub-questions, for example, between QUESTION 2.1 and QUESTION 2.2.
- You may use a non-programmable calculator.
- You are advised to use the attached DATA SHEETS.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions etc. where required.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1–1.10) in the ANSWER BOOK, for example 1.11 D.
1.1 The positional isomer of the molecule below is …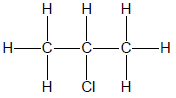



 (2)
(2)
1.2 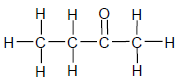
The IUPAC name for the compound above is …
- butanal.
- butanol.
- butanone.
- butanoic acid. (2)
1.3 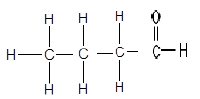
The structure above represents a/an …
- ketone.
- aldehyde.
- ester.
- carboxylic acid. (2)
1.4 Which of the following groups of elements can be used for doping?
- Group 3 and Group 5 elements
- Alkali metals (Group 1) and alkali earth metals (Group 2)
- All transition metals since they can conduct electricity
- Halogens (Group 7) and inert gases (Group 8) (2)
1.5 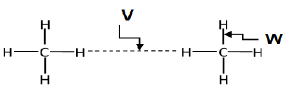
The correct labels for V and W are respectively:
V | W | |
A | Intramolecular forces | Intermolecular forces |
B | Intermolecular forces | Intramolecular forces |
C | Inter atomic forces | Chemical bonds |
D | Chemical bonds | Inter-atomic forces |
(2) [10]
QUESTION 2 (Start on a new page.)
Give ONE word for each of the following statements.
2.1 When a hydrocarbon burns in oxygen. (1)
2.2 Organic molecules with the same molecular formula, but different structural formulae. (1)
2.3 A large molecule composed of smaller monomer units covalently bonded to each other in a repeating pattern. (1)
2.4 A semiconductor doped with phosphorus (P), arsenic (As) or antimony (Sb) as an impurity. (1)
[4]
QUESTION 3 (Start on a new page.)
The diagram below represents the model of propene.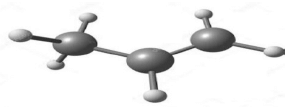
Propene is one of the most important organic compounds that is used in the industry to manufacture various products such as propanol and esters.
3.1
3.1.1 Define the term organic compound. (2)
3.1.2 Write down the general formula for alkenes. (1)
3.1.3 To which homologous series does propanol belong? (1)
3.1.4 What is the NAME of the functional group which propanol belongs to? (1)
3.1.5 Draw the structural formula of propan-2-ol. (2)
3.2 Propyl methanoate is the ESTER that is a product of an industrial process mentioned in the statement above. Use this information and answer the following questions.
3.2.1 Name the type of intermolecular forces found between esters and between alcohols. (2)
3.2.2 Write down the NAME of the carboxylic acid used to form the propyl methanoate. (1)
3.2.3 Draw the structural formula of the functional isomer of propyl methanoate. (2)
3.2.4 Draw the structural formula for the FUNCTIONAL GROUP of the isomer mentioned in QUESTION 3.2.3 above. (1)
3.3 Consider the organic compounds given below and answer the questions that follow.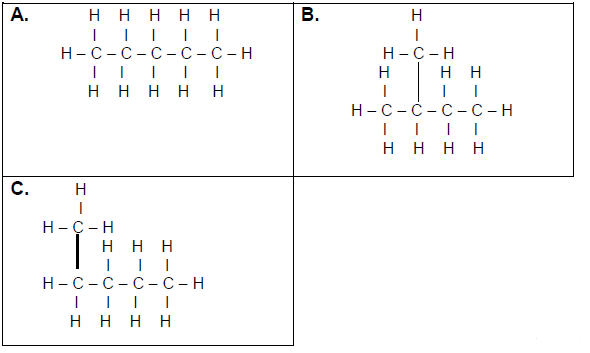
Write down:
3.3.1 ONE similarity between compounds A, B and C (1)
3.3.2 ONE observable difference between A and B (1)
3.3.3 The homologous series to which these compounds belong (1)
3.4 Write down the IUPAC names of the compounds represented by the following letters:
3.4.1 A (1)
3.4.2 B (2)
3.4.3 C (1)
3.4.4 Which of these compounds has the smallest surface area? Write only A, B or C. (1)
3.4.5 Explain your answer to QUESTION 3.4.4 above. (2)
3.5
3.5.1 Define the term plastic in words. (2)
3.5.2 Choose TWO industrial uses of polyethene from the list given in the table below.
USES | |
A | Electroplating |
B | Food packaging plastics |
C | Squeezable bottles |
D | Electrorefining |
E | Flexible water pipes |
F | Aluminium extraction |
(2 x 1) (2)
[27]
QUESTION 4 (Start on a new page.)
In the table below FIVE substances, as well as their molecular formula and viscosity, are given. Use the table to answer the questions which follow.
SUBSTANCE | MOLECULAR FORMULA | VISCOSITY | |
A | Pentane | C5H12 | X |
B | Chlorohexane | C6H11Cl | 0,695 |
C | Pent-2-ene | C5H10 | 0,210 |
D | Ethanol | C2Hn6O | 1,074 |
E | Propan-1-ol | C3H8O | 1,945 |
4.1 Define the term vapour pressure. (2)
4.2 Identify the TYPE of intermolecular force in:
4.2.1 Chlorohexane (1)
4.2.2 Pent-2-ene (1)
4.3 Use the table above to answer these questions.
How does the viscosity of chloro-hexane compare with the viscosity of pentane? Write only HIGHER or LOWER. Explain your answer. (2)
4.4 Explain, by referring to intermolecular forces and energy, which of the organic compounds from the table above will have the highest vapour pressure. (3)
4.5 Which intermolecular forces are common between pent-2-ene and ethanol? (2)
[11]
QUESTION 5 (Start on a new page.)
Hydrocarbons are famous for being the primary constituents of fossil fuels. Energy is obtained from fossil fuels through combustion of the fuel. Hydrocarbon combustion is the primary process in the burning of fossil fuels. Regardless of the type of hydrocarbon, the combustion produces the same products and large amounts of thermal heat are released.
5.1 Define the term hydrocarbon. (1)
5.2 Write down:
5.2.1 A balanced chemical reaction for the complete combustion of methane using a molecular formula (3)
5.2.2 The reaction conditions for the complete combustion of methane (1)
[5]
QUESTION 6 (Start on a new page.)
6.1 Consider the flow diagram below and answer the questions that follow.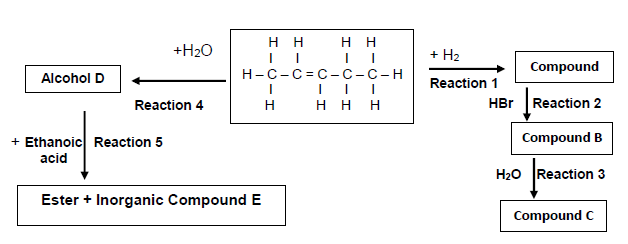
Write down the NAME/TYPE of the following:
6.1.1 Reaction 3 (1)
6.1.2 Reaction 4 (1)
6.1.3 Reaction 5 (1)
6.2 Write down the IUPAC name for the following compounds:
6.2.1 Secondary alcohol D (1)
6.2.2 Minor product compound B (1)
6.2.3 Inorganic compound E (1)
6.3 Write down the reaction conditions for the following reactions:
6.3.1 Reaction 1 (1)
6.3.2 Reaction 2 (1)
6.4 Draw the structural formula of compound C. (2)
6.5 Write down:
6.5.1 A balanced chemical reaction for Reaction 5 using structural formulae (4)
6.5.2 The NAME of the ester formed in Reaction 5 (1)
6.5.3 A balanced chemical reaction for Reaction 1 using structural formulae (3)
[18]
TOTAL: 75
NATIONAL SENIOR CERTIFICATE
DATA FOR TECHNICAL SCIENCES GRADE 12 PAPER 2 (CHEMISTRY)
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Avogadro’s constant | NA | 6,02 × 1023 mol-1 |
Molar gas constant | R | 8,31 J.K-1.mol-1 |
Standard pressure | pq | 1,013 × 105 Pa |
Molar gas volume at STP | Vm | 22,4 dm3∙mol-1 |
Standard temperature | Tθ | 273 K |
TABLE 2: FORMULAE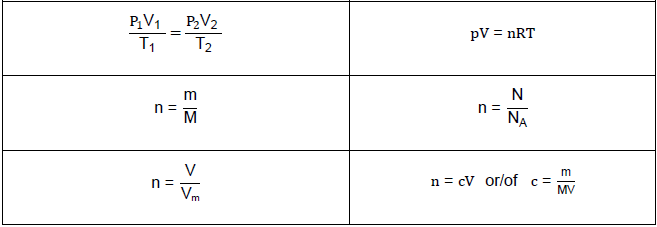
TABLE 3:THE PERIODIC TABLE OF ELEMENTS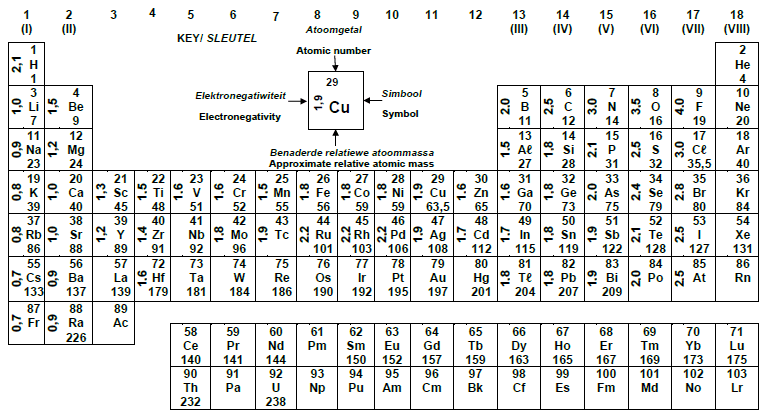
TABLE 4A: STANDARD REDUCTION POTENTIAL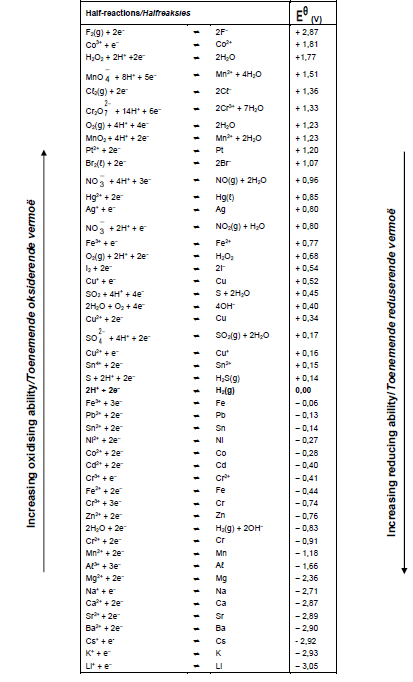
TABLE 4B:STANDARD REDUCTION POTENTIALS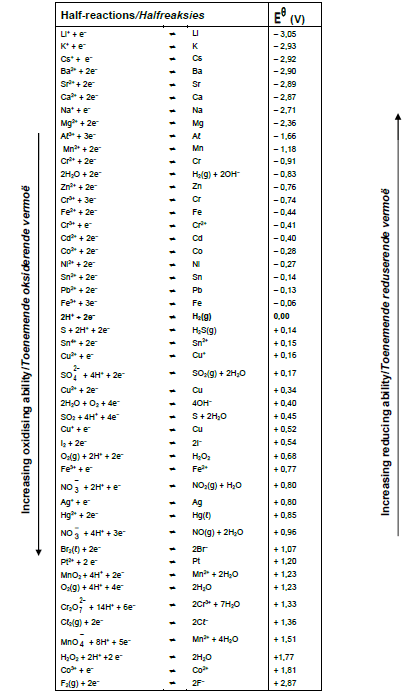
Technical Sciences Paper 1 Memorandum - Grade 12 June 2021 Exemplars
MEMORANDUM
QUESTION 1
1.1 A √√ (2)
1.2 D √√ (2)
1.3 C √√ (2)
1.4 A √√ (2)
1.5 B √√ (2)
1.6 C √√ (2)
1.7 D √√ (2)
1.8 A √√ (2)
1.9 D √√ (2)
1.10 D √√ (2) [20]
QUESTION 2
2.1
2.1.1 F1 = Normal force √ (1)
2.1.2 F2 = Weight √ (1)
2.2
2.2.1 Force of the block on the EARTH √(2)
2.2.2
- F4 = mg √
= 5 x 9,8 √
= 49 N √ (3)
2.3.1 Newton’s First Law √ - A body will remain at rest or continue moving with constant velocity unless a net force acts on it. √√ (3)
2.3.2 Fnet = 0 N √ (1)
[11]
QUESTION 3
3.1
3.1.1 To ensure that tension is uniform. √√ (2)
3.1.2
- A net force produces acceleration of an object in the direction of the net force. The acceleration is directly proportional to the net force and inversely proportional to the mass of the object. √√ (2)
OR - The net force acting on a body is equal to the rate of change of momentum in the same direction as the net force.
3.1.3
- FH = F cosθ √
= 40 cos 35° √
= 32,77 N
Fnet = ma √
80 kg mass: 50 kg mass:
Fnet = ma Fnet = ma
T – 6 = 80 a √ 32,77 – T √ = 50 a √
a = 0,21 m.s-2 √ (7)
3.1.4 DECREASES √ Horisontal component (of 40 N force) decreases √√ (3)
3.2
3.2.1 Mass (of the trolley) √ (1)
3.2.2 a α F √√ (if m constant and net force decreases, the acceleration decreases) OR (as net force increases acceleration increases) (2)
3.3 Experiment B √
Gradient of A > gradient of B √
1/mA > 1/mB √√
Therefore mA < mB (4)
[21]
QUESTION 4
4.1 In an isolated system the total linear momentum remains constant. √√ (2 or 0) (2)
4.2
- Σ pi = Σ pf
m1v1i + m2v2i = m1v1f + m2v2f √
16 000 + (2 000)(10,61) √= (800)(12) + 2 000 v2f √
v2f = 13,81 m.s-1 √ (4)
4.3
- Ektotal before = ½ mvA2 +½mvB2
= ½ x 800 x 202 √ + 112 500
= 272 500 J - Ektotal after = ½(800)122 √+ ½ (2 000)(13,81)2 √
= 248 316,1 J √ - Inelastic: Ek before > Ek after √ OR Ek before ≠ Ek after (5)
4.4
- Fnet Δt = Δp √
Fnet = (9 600 – 16 000 √)/0,15 √
= - 42 666,67 N
= 42 666,67 N, left/links √ (4)
[15]
QUESTION 5
5.1 Energy a body has because of its position above the ground √√ (2)
5.2
- Ek = ½ mv2 √
= ½ x 0,5 x 19,82 √
= 98,01 J √ (3)
5.3
- Ep lost= - Ek gained
= - 98,01 √√
98,01 = - mg(yf –yi)
98,01 √= - 0,5 x 9,8(yf – 0) √
yf = - 20 m - Emech bottom = Emech top
(mgh + 1/2mv2)bottom = (mgh + 1/2mv2)top √
0 + ½ (0,5 x 252) √ = ½ x 9,8 x hP √
hP = 31,89 m
h = 31,89 + 20 = 51,89 m √ (8)
5.4
- P =W/Δt √
= 37 350/20 √
= 1 867,5 W
P = 1867,5 / 746 √ = 2,50 hp √ (4)
[17]
QUESTION 6
6.1 Stress √ (1)
6.2
6.2.1
- Strain = Δl/L √
= (405 – 400) /400 √
= 0,0125 √ (3)
6.2.2
- Strain = F/A √
A = π r2 √
= π x (5/1000)2 √
= 7,85 x 10 -5 m2 - Strain = 30 000/7,85 x 10 -5 √
= 3,82 X 10 8 Pa √ (5)
6.3
6.3.1 Modulus of elasticity √ (1)
6.3.2 Hooke’s law √ (1)
6.3.3 Within the limits of elasticity√, stress is directly proportional to strain √ (2)
6.4
6.4.1 B √ (1)
6.4.2 A √ (1)
6.5
6.5.1 Elasticity √ (1)
6.5.2 Elastic band, bow, trampoline, spring diving board (Any TWO) √√ (2)
6.5.3 Restoring force √ (1)
[19]
QUESTION 7
7.1
7.1.1 Viscosity is the property of a fluid to oppose relative motion between two adjacent layers. √√ (2)
7.1.2 R √ Time of flow in R is highest . √√ (3)
7.1.3 smaller than √
Viscosity increases with increase in temperature. √√ (3)
7.1.4
- p = ρgh √
= 1000 x 9.8 x 10 √
= 98 00 Pa √ (3)
7.2
7.2.1 In a continuous liquid at equilibrium, the pressure applied at a point is transmitted equally to the other parts of the liquid. √√ (2)
7.2.2
- F1/A1= F2/A2 √
F1/(0,045) √= 20 000/0,28 √
F1 = 3 214,29 N √ (4)
[17]
QUESTION 8
8.1
8.1.1 Communication √ (1)
8.1.2 Images of bones √/Security machines at airports etcetera.(1)
8.2 Gamma rays √ (1)
8.3
- c = fλ √
3 x 108 = 5 x 1017 λ √
λ = 6 x 10-9 m √ (3)
8.4
- E = hf √
= h c/ λ
= 6.63 x10-34 x 3 x108/ 502x10-9 √
= 3.96 x 10-19 J √ (3)
[9]
QUESTION 9
9.1
9.1.1 Reflection √ (1)
9.1.2 Angle of incidence equal to angle of reflection √
Angle of incidence, angle of reflection and normal are in the same plane √ (2)
9.1.3 b is the angle of reflection √ b = 60º √ (2)
9.2 9.2.1 Breaking up of white light into its constituent colours √√ (2)
9.2.2 Red √ Highest wavelength √ The higher the wavelength the smaller the refraction√ (3)
9.3
9.3.1 Refraction √ (1)
9.3.2 Critical angle √ (1)
9.3.3 Total internal reflection √(1)
9.3.4 Communications √and medicine √ (2)
9.4
9.4.1 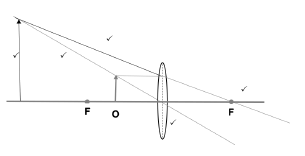 (5)
(5)
9.4.2 Upright √/ larger than the object/Virtual (Any one) (1)
[21]
TOTAL: 150
Technical Sciences Paper 1 Questions - Grade 12 June 2021 Exemplars
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- Write your FULL NAME and SURNAME in the appropriate spaces on the ANSWER SHEET.
- Answer ALL the questions.
- Start each question on a NEW page in the ANSWER BOOK.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Number the answers correctly according to the numbering system used in this question paper.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, et cetera where required.
- You are advised to use the attached DATA SHEET.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write the letter (A–D) next to the question numbers (1.1–1.10) in the ANSWER BOOK, for example 1.11 E.
1.1 Which ONE of the following is defined as the tendency of an object to resist a change in its state of motion?
- Inertia
- Force
- Weight
- Impulse (2)
1.2 The SI unit of the quantity rate of change of momentum is ...
- kg.m.s-1.
- N.s.
- J.
- N. (2)
1.3 An object has a constant acceleration of 0,2 m.s-2.
The constant acceleration of 0,2 m.s-2 means that the object’s …
- speed is constant.
- direction is changing.
- velocity changes by 0,2 m.s-1 every second.
- displacement changes by 0,2 m. s-1 every second. (2)
1.4 Which of the following quantity (ies) is/are CONSERVED in both ELASTIC and INELASTIC collisions?
- Momentum only
- Kinetic energy
- Both momentum and kinetic energy
- Neither momentum nor kinetic energy (2)
1.5 Airbags in modern cars provide more safety during an accident.
Which ONE of the following combinations is CORRECT regarding TIME OF CONTACT and the NET FORCE acting on a passenger during a collision in a car fitted with airbags?
TIME OF CONTACT | NET FORCE | |
A | Increases | Increases |
B | Increases | Decreases |
C | Decreases | Increases |
D | Decreases | Decreases |
(2)
1.6 When a force F is applied on an object P by an object Q, the object P will exert a force of equal magnitude on object Q in the opposite direction.
What is the NAME of the law stated above?
- Newton’s First law
- Newton’s Second law
- Newton’s Third law
- Pascal’s Law (2)
1.7 Mechanical energy is defined as …
- product of force and time.
- work done divided by time .
- product of force and veloc ity.
- sum of gravitational potential energy and kinetic energy. (2)
1.8 The ratio of change in dimension to the original dimension is called …
- strain
- stress
- elasticity
- elastic limit (2)
1.9 In the ray diagram below an object is placed at point P beyond the focal point F of a lens.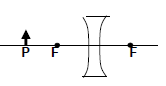
The characteristics of the image of the object placed at point P as shown in the diagram will be …
- real, smaller and upright.
- real, smaller and inverted.
- virtual, smaller and inverted.
- virtual, smaller and upright. (2)
1.10 Light rays that enter the eye are refracted by the eye lens and cornea so that they can focus on the back of the eye.
If the rays of light do not focus on the back of the eye as shown in the diagram below, a blurry image will result which may be corrected by glasses or contact lenses.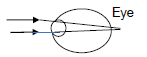
Which ONE of the following CORRECTLY gives the TYPE of lens to be used to correct the condition and the reason for using the lens?
TYPE OF LENS | REASON FOR USING THE LENS | |
A | Concave | To diverge light entering the eye |
B | Concave | To converge the light entering the eye |
C | Convex | To diverge light entering the eye |
D | Convex | To converge light entering the eye |
(2) [20]
QUESTION 2 (Start on a new page.)
2.1 A block of mass 5 kg is pushed by means of a stick, held at an angle of 20° to the horizontal as shown in the diagram below. The block moves horizontally to the right.
Part APC is FRICTIONLESS while CD is a ROUGH surface.
The force diagram below shows all the forces acting on the box BEFORE it reaches point P.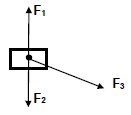 Name the following forces:
Name the following forces:
2.1.1 F1 (1)
2.1.2 F2 (1)
2.2 F2 and another force, F4, are ACTION-REACTION pairs.
2.2.1 Describe force F4, the action-reaction pair of force F2. (2)
2.2.2 Calculate the magnitude of F4. (3)
2.3 When the block reaches point P the stick is REMOVED, and the block continues moving until it reaches point D.
2.3.1 Name and state the law that explains why the block continues moving after the stick is removed at point P. (3)
2.3.2 Write down the value of the net (resultant) force acting on the block as it moves between points P and C. (1)
[11]
QUESTION 3 (Start on a new page.)
3.1 Two crates X and Y, connected by a light inextensible string, are pulled with a force of 40 N that acts at 35° to the horizontal, as shown in the diagram below.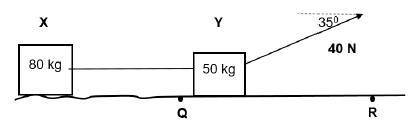
The frictional force acting on crate X is 6 N while part QR is FRICTIONLESS.
3.1.1 Explain why the string must be inextensible. (2)
3.1.2 State Newton’s Second Law of motion in words. (2)
3.1.3 Calculate the magnitude of the acceleration of the crates before crate X reaches point Q. (7)
3.1.4 What will happen to the acceleration calculated in QUESTION 3.1.3, if the angle 35° shown in the diagram is increased to 60°? Write only INCREASES, DECREASES or REMAINS THE SAME. Explain your answer. (3)
3.2 Learners perform an investigation to determine the relationship between net force and acceleration.
The learners performed TWO experiments (A and B), using a different mass in each experiment.
The learners recorded their results for experiments (A and B) in a table and used them to draw the graph shown below.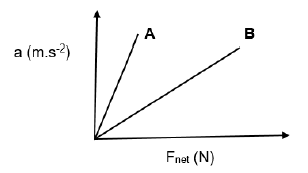
For investigation A, write down the:
3.2.1 Controlled variable (1)
3.2.2 Conclusion that can be drawn from the graph about the relationship between acceleration and net force (2)
3.3 In which experiment was a LARGER mass used? Use information from the graph to explain the answer. (4)
[21]
QUESTION 4 (Start on a new page.)
4.1 Two cars, P and Q, of masses 800 kg and 2 000 kg respectively, move in the same direction, east, and collide as shown in the diagrams below.
Before the collision car P is moving at a speed of 20 m.s-1 and car Q has a kinetic energy of 112 500 J.
BEFORE THE COLLISION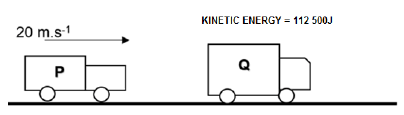
AFTER THE COLLISION
After the collision both cars, P and Q, continue to move east. Car P has a velocity of 12 m.s-1 after the collision.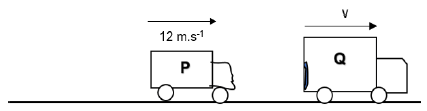
4.1 State the principle of conservation of momentum. (2)
4.2 Calculate the velocity of car Q after the collision. (4)
4.3 Determine by calculation whether the collision is ELASTIC or INELASTIC. (5)
4.4 The time of contact during the collision is 0,15 s.
Calculate the net force on car P during the collision. (4)
[15]
QUESTION 5 (Start on a new page.)
A stone of mass 0,5 kg is dropped from rest, at the edge of a building of height h metres above the ground. When the stone reaches point P, below its starting point, its velocity is 19,8 m.s-1 downwards.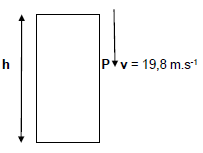
5.1 Define gravitational potential energy. (2)
5.2 Calculate the kinetic energy of the stone at point P on its way down. (3)
5.3 The stone strikes the ground and bounces off vertically upwards with a speed of 25 m.s-1. On its way up, the stone reaches point P and returns to the ground.
Use energy principles to calculate the height of the building, h. (IGNORE AIR RESISTANCE.) (8)
5.4 The engine of a racing car does 37 350 Joules of work in a race. Calculate the power output of the engine if the car travels for 20 s. Convert the units to horsepower. (4)
[17]
QUESTION 6 (Start on a new page.)
A cylindrical bar of length 400 mm is stretched to 405 mm when a force of 30 000 N is exerted on the bar.
The diameter of the bar is 50 mm.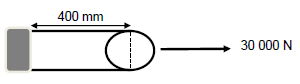
6.1 Give a term for the internal restoring force per unit area of a body. (1)
6.2 Calculate the:
6.2.1 Strain on the bar (3)
6.2.2 Stress experienced by the bar (5)
6.3 The force exerted on the bar is changed and each time the force is changed the stress and strain are calculated.
The graph of stress vs strain for the bar is shown below.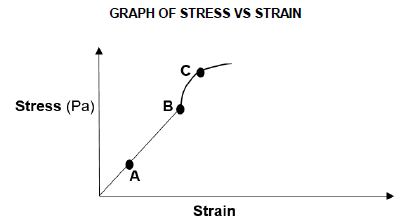
6.3.1 What does the gradient of the graph represent? (1)
6.3.2 Name the law that is investigated in this experiment. (1)
6.3.3 State the law mentioned in QUESTION 6.3.2 in words. (2)
6.4 Which letter (A, B or C):
6.4.1 Indicates the elastic limit? (1)
6.4.2 Lies in the elastic region? (1)
6.5 Perfectly elastic bodies are characterised by a property whereby the body regains its original shape and size when the deforming force is removed.
Write down:
6.5.1 A term for the underlined phrase (1)
6.5.2 TWO examples of objects that are perfectly plastic (2)
6.5.3 The NAME of a force that is always equal and opposite to the deforming force (1)
[19]
QUESTION 7 (Start on a new page.)
7.1 A group of learners carried out an investigation to compare the viscosities of three different liquids P, Q and R at 25 °C.
The learners dropped the same marble in equal columns of the liquids P, Q and R in identical containers. They then measured the time it took the marble to fall to the bottom of each liquid.
tp, tq and tr are the times taken by the marble to fall to the bottom of the container in liquids P, Q and R respectively.
7.1.1 Define the term viscosity. (2)
7.1.2 Which liquid (P, Q or R) has the HIGHEST viscosity? Explain the answer. (3)
The THREE liquids (P, Q and R) are heated to 40 °C and the experiment is repeated at 40 °C. 7.1.3 How will the time of flow of the liquids be affected? Write only HIGHER, LOWER or THE SAME. Explain the answer. (3)
7.1.4 Calculate the pressure at a depth of 10 m in liquid A given that the density of liquid A is equal to 1000 kg.m-3. (3)
7.2 A hydraulic lift at a fuel station uses compressed air to lift a truck weighing 20 000 N.
The compressed air exerts a force on a small piston (PISTON 1) with a circular cross-sectional area of 0,045 m2. The pressure is transmitted by a hydraulic fluid to a larger piston (PISTON 2) of area 0,28 m2. The diagram below shows the hydraulic lift.
7.2.1 State Pascal’s principle in words. (2)
7.2.2 Calculate the magnitude of the minimum force that the compressed air must exert to lift the truck. (4)
[17]
QUESTION 8 (Start on a new page.)
The diagrams below show electromagnetic spectrum. The electromagnetic spectrum is the complete range of electromagnetic wave frequencies and wavelengths.
8.1 Write down ONE use of each radiation below:
8.1.1 Microwaves (1)
8.1.2 X-rays (1)
8.2 Name the electromagnetic wave that has the HIGHEST energy photons. (1)
8.3 An electromagnetic wave has a frequency of 5 x1017 Hz.
Calculate the wavelength of this wave. (3)
8.4 Consider an electromagnetic light wave with a wavelength of 502 nm. Calculate the energy of a photon of this light. (3)
[9]
QUESTION 9 (Start on a new page.)
9.1 Use the ray diagram below to answer the questions that follow.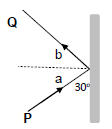
9.1.1 Write down the NAME of the phenomenon illustrated above. (1)
9.1.2 State TWO requirements for the phenomenon in the diagram above. (2)
9.1.3 Write down the NAME and the VALUE of angle b (2)
9.2 Visible light undergoes dispersion when it strikes glass.
9.2.1 Define dispersion of light. (2)
9.2.2 Which colour of light is least refracted when light undergoes dispersion? Explain the answer in terms of wavelength. (3)
9.3 In the diagram below ray of light strikes a glass-air interface. The light bends as it enters a medium of different optical density. Glass is more optically dense than air.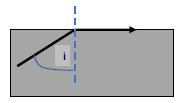
9.3.1 Write down a term for the underlined sentence. (1)
9.3.2 What special name is given to the angle of incidence , i, when the effect in the diagram occurs? (1)
9.3.3 Name the phenomenon that occurs when the angle i is increased (1)
9.3.4 Name TWO applications of the phenomenon mention in QUESTION 9.3.3. (2)
9.4 Consider the diagram below in which an object of height 1 cm is placed at point O between optical centre and focal point of a convex lens. The focal length is 2 cm.
9.4.1 On the diagram sheet attached to this question paper, use a ruler to construct accurately the position of the image. (5)
9.4.2 Write down ONE property of the image formed in QUESTION 9.4.1 above. (1)
[21]
TOTAL: 150
DATA FOR TECHNICAL SCIENCES
GRADE 12
PAPER 1
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m·s-2 |
Speed of light in a vacuum | c | 3,0 x 108 m·s-1 |
Planck's constant | h | 6,63 x 10-34 J·s |
Permittivity of free space | ɛ0 | 8,85 × 10-12 F.m-1 |
TABLE 2: FORMULAE
FORCE
WORK, ENERGY AND POWER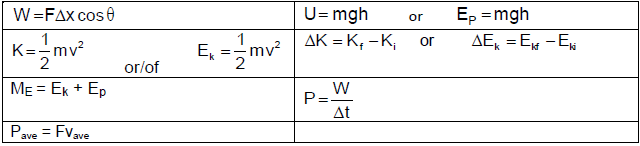
ELASTICITY, VISCOSITY AND HYDRAULICS
WAVES, SOUND AND LIGHT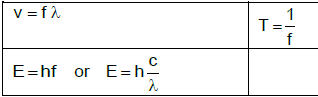
ELECTROSTATICS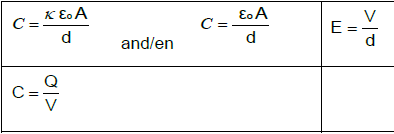
CURRENT ELECTRICITY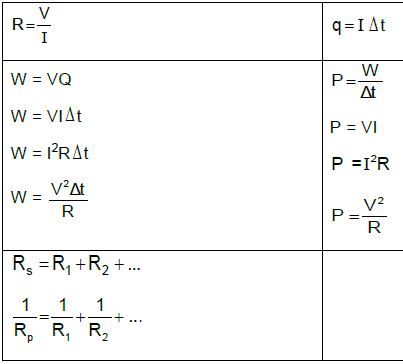
ELECTROMAGNETISM
ELASTICITY, VISCOSITY AND HYDRAULICS
9.4.1 DIAGRAM SHEET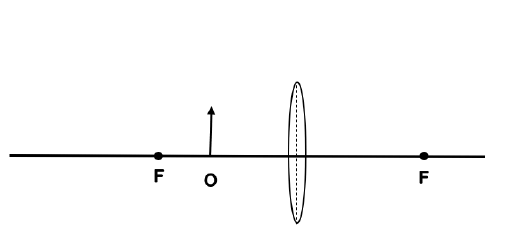
Technical Mathematics Paper 2 Memorandum - Grade 12 June 2021 Exemplars
NOTE:
- Continuous accuracy (CA) applies ONLY where indicated in this marking guideline.
- Assuming values/answers in order to solve a problem is unacceptable.
MARKING CODES | |
M | Method |
A | Accuracy |
AO | Answer only |
CA | Consistent accuracy |
F | Formula |
I | Identity |
R | Rounding |
S | Simplification |
ST | Statement |
RE | Reason |
ST/RE | Statement and correct reason |
SF | Substitution into correctly the correct formula |
NPU | No penalty for omitting units |
QUESTION 1 | ||||||||
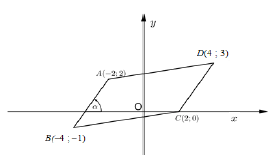 | ||||||||
1.1 |
| √ SF | (2) | |||||
| 1.2 | mCD = y2 - y1 x2 - x1 = 3 - 0 = 0 - 3 4 - 2 2 - 4 = 3/2 Equation of CD y - y1 = m(x - x1) y - y1 = m(x - x1) y - 0 = 3/2(x - 2) OR y - 3 = 3/2(x - 4) y = 3/2x - 3 y = 3/2x - 3 | √ SF √ A √ CA gradient √ SF CA √ CA | (4) | |||||
| 1.3 | mAB = 3/2 (opp sides of II''') | √ CA | (1) | |||||
| 1.4 | tan ∝ = 3/2 ∝ = 56,31º | √ M √ CA √ CA | (2) | |||||
| 1.5 | 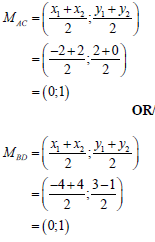 | √ SF A OR √SF A | (2) | |||||
| 1.6 | mnew line = - 1 mCD Equation of new line y - y1 = m(x - x1) y - 1 = -2/3 (x - 0) y = -2/3x + 1 | √ M CA √ SF CA √ CA | (3) | |||||
| 14 | ||||||||
| QUESTION 2 | |||
 | |||
| 2.1.1 | x2 + y2 = r2 = (2(√2)2 x2 + y2 = 8 | √ SF A √ CA | (2) |
| 2.1.2 | y = 4 - x ..... eq 1 OR x = 4 - y ..... eq 1 | √ equation1 M A OR √ equation 1 M A | (5) |
| 2.1.3 | No, ?? ⊥ ?? shortest distance to the centre is Q.No, ?? ⊥ ?? shortest distance to the centre is Q. | √ No √√ Justification | (2) |
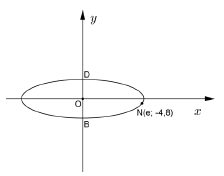 | |||
| 2.2.1 | B(0;-√64) = B(0;8) | √A √A | (2) |
| 2.2.2 | 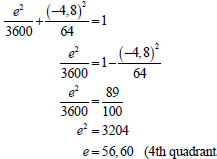 | √ SF A √ S CA √ CA | (3) |
| [14] | |||
| QUESTION 3 | |||
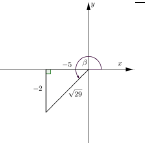 | |||
| 3.1.1 | r2 = (-5)2 + (-2)2 r = √29 ∴sin β = -2 √29 | √ quadrant A √ quadran A √ value of r A √ value of ratio CA | (3) |
| 3.1.2 | cot (360º - β) + 1 = -cot β + 1 = -5/2 + 1 = -3/2 | √ -cot β I √ S CA | (2) |
| 3.2.1 | sin (θ + α) =sin (72º + 96º) = 0,21 | √ S A √ S CA AO Full marks | (2) |
| 3.2.2 | sec α + sin 5π = 1 + sin 150º 6 cos 96º = 1 + 0,5 cos 96º = -9,07 | √ 1 A cos 96º √ 0,5 √ CA AO Full marks | (3) |
| 3.3 | 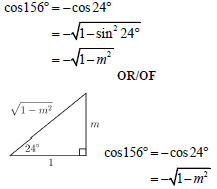 | √ -cos 24º OR √ -cos24º | (3) |
| [13] | |||
| QUESTION 4 | |||
| 4.1 | 1 | √ S A | (1) |
| 4.2 | 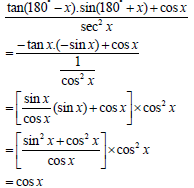 | √ -tanx I A √ -sin I A √ 1 I A cos2x √ tan x = sin x I A cos x √ S CA √ sin2x + cos2x = 1 I A √ S CA | (7) |
| 4.3 | 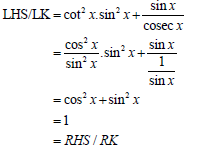 | √ cotx = cosx I A sin x √ 1 I A sin x √ sin2x + cos2x = 1 I A | (3) |
| 4.4.1 | sec 2x = 2 ∴ cos 2x = ½ Ref ∠ = 60º ∴ x - 30º = 180º - 56,3º or x - 30º = 360º - 56,3º ∴ x - 30º = 123,7º or x - 30º = 303,7º ∴ x = 153,7º or x = 333,7º | √ tan(x - 30º) = -3/2 S A √ reference √ 123,7º CA √ 303,7º CA √ 153,7º and 333,7º CA | (4) |
| 4.4.2 | (5) | ||
| [20] | |||
| QUESTION 5 | |||
 | |||
| 5.1 | see diagram above | √ x-intercept A √ endpoints A √ turning points A | (3) |
| 5.2.1 | Amplitudeg = 1 | √ A | (1) |
| 5.2.2 | periodf = 360º = 180º 2 | √ A | (1) |
| 5.2.3 | rangeg : y∈ [-1;1] | √ endpoints A √ notation A | (2) |
| 5.2.4 | ƒ(135º) - g(135º) = 0 - 1 - 1 | √ function values A √ CA AO Full marks | (2) |
| 5.2.5 | x∈{0º;180º;360º} | √ A | (3) |
| 5.2.6 | x∈(225º;315º) or 225º < x < 315º | √ endpoints A √ notation A | (2) |
| 5.2.7 | x∈[135º;315º] or 135º ≤ v ≤ 315º | √ endpoints A √ notation A | (2) |
| 5.2.8 | x∈[90º;180º) or 90º < x < 180º | √ endpoints A √ notation A | (2) |
| [18] | |||
| QUESTION 6 | |||
| 6.1 | sin P = sin Q p q | √ A | (1) |
| 6.2 |  | ||
| 6.2.1 | In ΔABC: sin C = sin A c a sin C = sin 80º 10 11 sin C = 0,8952.....º C = 63,534.......º B = 180º - 80º - 63,534....º≈36 | √ SF A √ S CA √ value of c CA √ value of B R | (4) |
| 6.2.2 | In ΔDBC: DC2 = DB2 + BC2 - 2DB.BC cos B = 62 +112 - 2 × 6 × 11 cos 36º = 950,20975...... DC = 7,09cm | √ F A √ SF CA √ S CA √ CA NPU | (4) |
| 6.2.3 | Area ΔDBC = ½DB.BC sin B = ½ × 6 × 11 sin36º = 19,40cm2 | √ F A √ SF CA √ S CA NPU | (3) |
| 6.2.4 | In ΔABC: b = a sin B sin A ∴ b = 11 or sin36º sin80º ∴ b = 11sin36º sin80º ∴ b = 6,57 units In ΔABC: ∴ b = 10 sin36º sin63,53º ∴ b = 10sin36º sin63,53º ∴b = 6,57 units | √ SF CA √ S CA √ value of CA | (3) |
| [15] | |||
| QUESTION 7 | |||
| 7.1 | Bisect the chord | √ A | (1) |
| 7.2 |  | ||
| 7.2.1 | RT = 2cm (line from centre ⊥ to chord) ∴ PT = 4 cm | √ ST √ RE √ ST NPU | (3) |
| 7.2.2 | OR2 = OP2 - PR2 (Pythagoras) = 82 - 22 = 60 OR = 2√15 LR = 8 - 2√15 ∴ LR = 0,25 units | √ M Pythagoras √ ST A √ length of OR S CA √ length of LR S CA NPU | (4) |
| [8] | |||
| QUESTION 8 | |||
| 8.1 | Same point | √ A | (1) |
 | |||
| 8.2.1 | DCE = DEC (tangents from common point) DCE = DEC =180º - 46º (∠s of Δ and ∠s opp = sides) 2 = 67º F = 67º (tan-chord) CGD = x = 67º | √ ST √RE √ ST RE √ ST √RE √ ST RE | (6) |
| 8.2.2 | From 8.2.1 DCE = DGC ∴ CGD is a circle (converse tan-chord th) | √ ST √ RE | (2) |
| 8.2.3 | EGD = ECD (∠s in same segment) ∴ EGD = 67º ∴ GEF = 67º (alt ∠ s; GD II FE) | √ ST √ RE √ ST RE | (3) |
| 8.2.4 | FGE = 46º [Int ∠s of Δ or ∠s on str lineor ext ∠ of cyclic quad] | √ ST √ RE √ RE (Any two) | (3) |
| 8.3 | 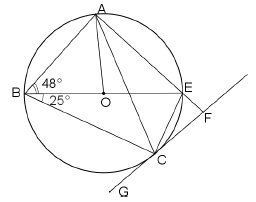 | ||
| 8.3.1 | BAE = 90º (∠ in semi-circlce) | √ ST √ RE | (2) |
| 8.3.2 | AOE = 96º (∠ at center = 2 × ∠ at circumf) | √ ST √ RE | (2) |
| 8.3.3 | CEF = 73º (ext ∠ of cyclic quad) | √ ST √ RE | (2) |
| 8.3.4 | ECF = 25º (tan-chord) | √ ST √ RE | (2) |
| 8.3.5 | ACE = 48º (∠s in the same segm) | √ ST √ RE | (2) |
| 8.3.6 | AEC = 107º (∠s on straight line OR opp ∠s of cyclic quad) ACG = 107º (tan-chord) | √ ST √ RE √ ST RE | (3) |
| [28] | ||
| QUESTION 9 | |||
| 9.1 | proportionally | √ A | (1) |
 | |||
| 9.2.1 | AE = AH (line III one side of Δ OR prop th; EH II FC) EF HC | √ ST √ RE | (2) |
| 9.2.2 | AE = AH (from 9.2.1) EF HC 3 = 6 EF 5 EF = 15 6 = 5 2 | √ ST √ CA √ ST √ CA √ ST √ CA | (3) |
| 9.2.3 | BF = 7 - EF = 7 - 5 2 = 9 2 | √ ST √ CA | (1) |
| 9.2.4 | In ΔBEG: BC = BF (line II one side of Δ OR prop th; EH III FC) CG FE = 4,5 2,5 = 1,8 < 3 | √ ST √ RE √ ST √ conclusion | (3) |
| [10] | |||
| QUESTION 10 | |||
 | |||
| 10.1 | In ΔACD and ΔAEB: 1) A is common 2) C = E1 ( ext ∠ of cyclic quad) 3) D = B1 (Int ∠s of Δ or ext ∠ of cyclic quad) ∴ ΔACD III ΔAEB (AAA) | √ ST √ RE √ ST √ mark is either for 3rd angle or for the reason AAA | (3) |
| 10.2 | AC = CD (ΔACD /// ΔAEB) AE EB ∴ AC = CD (AE = DC; given) CD EB ∴ CD2 = AC.EB | √ ST √ RE √ ST A | (3) |
| 10.3 | CD2 = 13 × 3 CD = √39 ≈ 6,24 cm | √ ST A √ M A √ Value of CD CA | (3) |
| [10] | |||
| Total: | 150 | ||
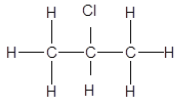
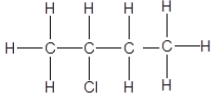
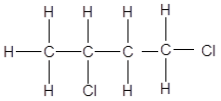
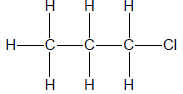 (2)
(2)