Adele
MATHEMATICS PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICS
PAPER 2
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
An organisation decided that it would set up blood donor clinics at various colleges. Students would donate blood over a period of 10 days. The number of units of blood donated per day by students of college X is shown in the table below.
| DAYS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| UNITS OF BLOOD | 45 | 59 | 65 | 73 | 79 | 82 | 91 | 99 | 101 | 106 |
1.1Calculate:
1.1.1 The mean of the units of blood donated per day over the period of 10 days (2)
1.1.2 The standard deviation of the data (2)
1.1.3 How many days is the number of units of blood donated at college X outside one standard deviation from the mean? (3)
1.2 The number of units of blood donated by the students of college X is represented in the box and whisker diagram below.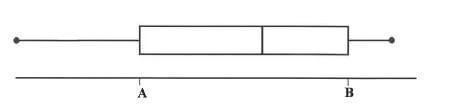
1.2.1 Describe the skewness of the data. (1)
1.2.2 Write down the values of A and B, the lower quartile and the upper quartile respectively, of the data set. (2)
1.3 It was discovered that there was an error in counting the number of units of blood donated by college X each day. The correct mean of the data is 95 units of blood.
How many units of blood were NOT counted over the ten days? (1) [11]
QUESTION 2
The table below shows the number of hours that a sales representative of a company spent with each of his nine clients in one year and the value of the sales (in thousands of rands) for that client.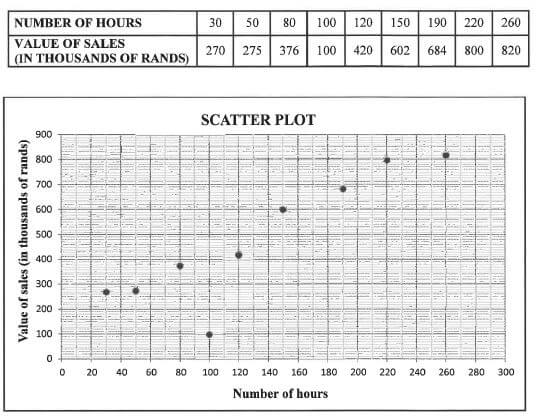
2.1Identify an outlier in the data above. (1)
2.2 Calculate the equation of the least squares regression line of the data. (3)
2.3 The sales representative forgot to record the sales of one of his clients. Predict the value of this client's sales (in thousands of rands) if he spent 240 hours with him during the year. (2)
2.4 What is the expected increase in sales for EACH additional hour spent with a client? (2) [8]
QUESTION 3
In the diagram, P, Q(-7 ; -2), R and S(3 ; 6) are vertices of a quadrilateral. R is a point on the x-axis. QR is produced to N such that QR = 2RN. SN is drawn. PTO = 71,57° and SRN = θ.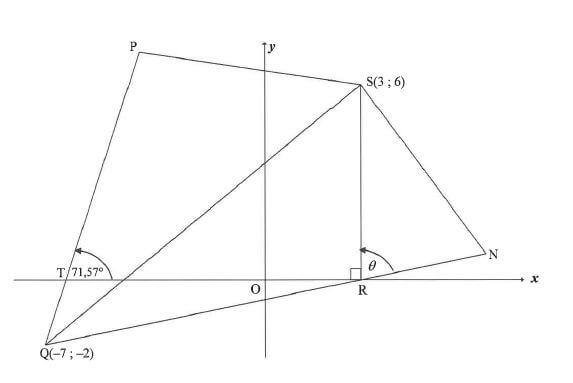
Determine:
3.1The equation of SR (1)
3.2 The gradient of QP to the nearest integer (2)
3.3 The equation of QP in the form y = mx + c (2)
3.4 The length of QR. Leave your answer in surd form. (2)
3.5 tan(90° - θ) (3)
3.6 The area of ΔRSN , without using a calculator (6) [16]
QUESTION 4
In the diagram, PKT is a common tangent to both circles at K(a ; b). The centres of both circles lie on the line y = ½x. The equation of the circle centred at 0 is x2 + y2 =180. The radius of the circle is three times that of the circle centred at M. 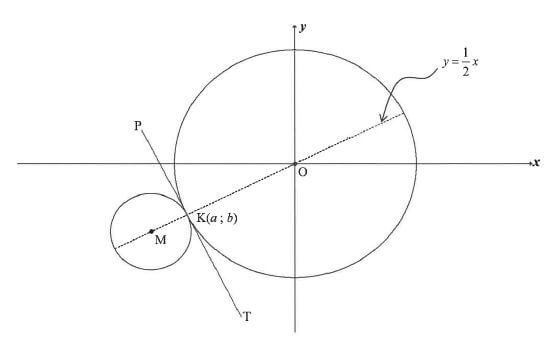
4.1 Write down the length of OK in surd form. (1)
4.2 Show that K is the point (-12 ; - 6). (4)
4.3 Determine:
4.3.1 The equation of the common tangent, PKT, in the form y = mx + c (3)
4.3.2 The coordinates of M (6)
4.3.3 The equation of the smaller circle in the form (x — a)2 + (y — b)2 = r 2 (2)
4.4 For which value(s) of r will another circle, with equation x2 + y2 = r 2, intersect the circle centred at M at two distinct points? (3)
4.5 Another circle, x2 + y2 + 32x +16y + 240 = 0 , is drawn. Prove by calculation that this circle does NOT cut the circle with centre M(-16 ; -8). (5) [24]
QUESTION 5
5.1 If cos 2θ= - 5 , where 2θ ∈ [180°; 270º] , calculate, without using a calculator, the values in simplest form of:
6
5.1.1 sin2θ (4)
5.1.2 sin2θ (3)
5.2 Simplify sin(180° - x).cos(-x) + cos(90° + x).cos(x -180°) to a single trigonometric ratio. (6)
5.3 Determine the value of sin 3x.cos y + cos 3x. sin y if 3x + y = 270° (2)
5.4 Given: 2 cos x = 3 tan x
5.4.1 Show that the equation can be rewritten as 2 sin 2 x + 3 sin x - 2 = 0. (3)
5.4.2 Determine the general solution of x if 2 cos x = 3 tan x. (5)
5.4.3 Hence, determine two values of y, 144° ≤ y ≤ 216°, that are solutions of 2 cos 5y = 3 tan 5y. (4)
5.5 Consider: g(x) = - 4 cos(x + 30°)
5.5.1 Write down the maximum value of g(x). (1)
5.5.2 Determine the range of g(x) + 1. (2)
5.5.3 The graph of g is shifted 60° to the left and then reflected about the x-axis to form a new graph h. Determine the equation of h in its simplest form. (3) [33]
QUESTION 6
PQ and AB are two vertical towers.
From a point R in the same horizontal plane as Q and B, the angles of elevation to P and A are θ and 2θ respectively.
AQR = 90° + θ, QAR = θ and QR = x .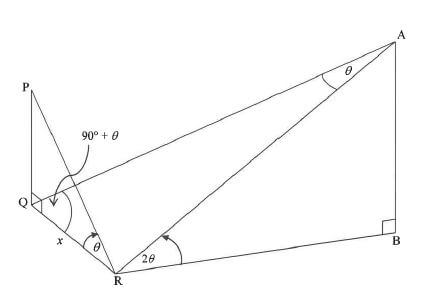
6.1 Determine in terms of x and θ :
6.1.1 QP (2)
6.1.2 AR (2)
6.2 Show that AB = 2x cos2θ (4)
6.3 Determine AB if θ = 12°. (2) [10]
QP
QUESTION 7
In the diagram, PQRT is a cyclic quadrilateral in a circle such that PT = TR. PT and QR are produced to meet in S. TQ is drawn. SQP = 70°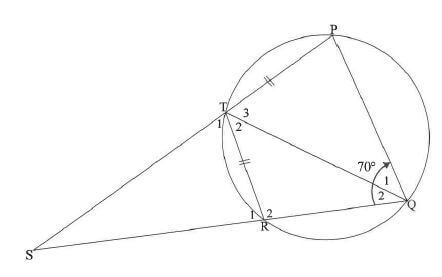
7.1 Calculate, with reasons, the size of:
7.1.1 T1 (2)
7.1.2 Q1 (2)
7.2 If it is further given that PQ ΙΙ TR:
7.2.1 Calculate, with reasons, the size of T2 (2)
7.2.2 Prove that TR = RQ (2) [8]
TS RS
QUESTION 8
In the diagram, PR is a diameter of the circle with centre O. ST is a tangent to the circle at T and meets RP produced at S. SPT = x and S = y.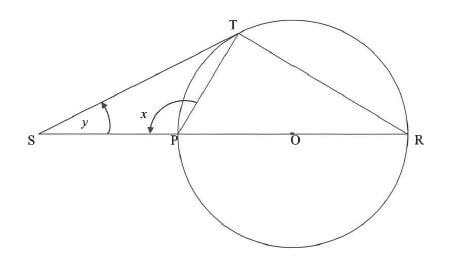
Determine, with reasons, y in terms of x. [6]
QUESTION 9
In the diagram, DEFG is a quadrilateral with DE = 45 and GF = 80. The diagonals GE and DF meet in H. GDE = FEG and DGE = EFG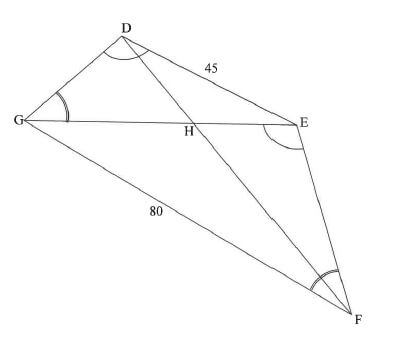
9.1 Give a reason why ΔDEG III ΔEGF. (1)
9.2 Calculate the length of GE. (3)
9.3 Prove that ΔDEH III ΔFGH. (3)
9.4 Hence, calculate the length of GH. (3) [10]
QUESTION 10
10.1 In the diagram, 0 is the centre of the circle with A, B and C drawn on the circle.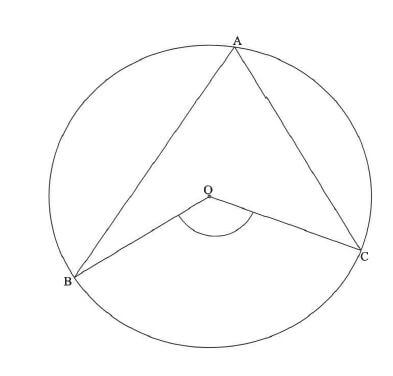
Prove the theorem which states that BOC = 2A. (5)
10.2 In the diagram, the circle with centre F is drawn. Points A, B, C and D lie on the circle. Chords AC and BD intersect at E such that EC = ED. K is the midpoint of chord BD. FK, AB, CD, AF, FE and FD are drawn. Let B = x .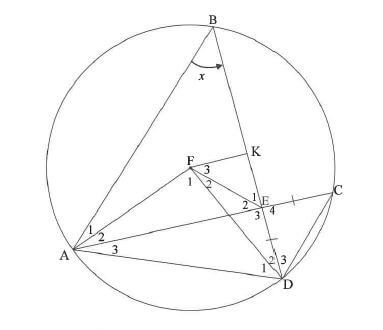
10.2.1 Determine, with reasons, the size of EACH of the following in terms of x:
- F1 (2)
- C (2)
10.2.2 Prove, with reasons, that AFED is a cyclic quadrilateral. (4)
10.2.3 Prove, with reasons, that F3 = x (6)
10.2.4 If area ΔAEB = 6,25 x area ΔDEC, calculate AE (5) [24]
ED
TOTAL:150

MATHEMATICAL LITERACY PAPER 1 GRADE 12 ADDENDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICAL LITERACY
PAPER 1
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
ADDENDUM
MATHEMATICAL LITERACY PAPER 2 GRADE 12 ADDENDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICAL LITERACY
PAPER 2
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
ADDENDUM
MATHEMATICAL LITERACY PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICAL LITERACY
PAPER 2
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of FOUR questions. Answer ALL the questions.
-
2.1 Use the ANNEXURES in the ADDENDUM to answer the following questions:- ANNEXURE A for QUESTION 1.2
- ANNEXURE B for QUESTION 2.1
- ANNEXURE C for QUESTION 3.3
- ANNEXURE D for QUESTION 4.3
2.2 Answer QUESTION 4.1.3 on the ANSWER SHEET attached.
2.3 Write your centre number and examination number in the spaces on the ANSWER SHEET. Hand in the ANSWER SHEET with your ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Round off ALL final answers appropriately according to the given context, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Maps and diagrams are NOT drawn to scale, unless stated otherwise.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1
The Rand Show is an annual event held in Gauteng. The Abrahams family, consisting of two adults aged 45 and 48, two children aged 6 and 14 and a grandmother aged 73, planned to visit the Rand Show. TABLE 1: DURATION AND TICKET PRICES OF THE 2017 RAND SHOW
| |||||||||||||||||||||||
Use the information above to answer the questions that follow.
1.1.1 Calculate the total number of hours the Rand Show will be open to visitors for the full duration of the show. (3)
1.1.2 Calculate the amount of VAT payable on a teen's ticket. (3)
1.1.3 Determine the probability (in simplified form) of randomly selecting a Friday visit to the Rand Show. (3)
1.1.4 The family visited the Rand Show on 23 April 2017. Mrs Abrahams stated that if the family had visited the Rand Show on 20 April instead of 23 April, they would have saved more than 35% on the total cost of the tickets. Verify, showing ALL calculations, whether her statement is valid. (9)
1.2
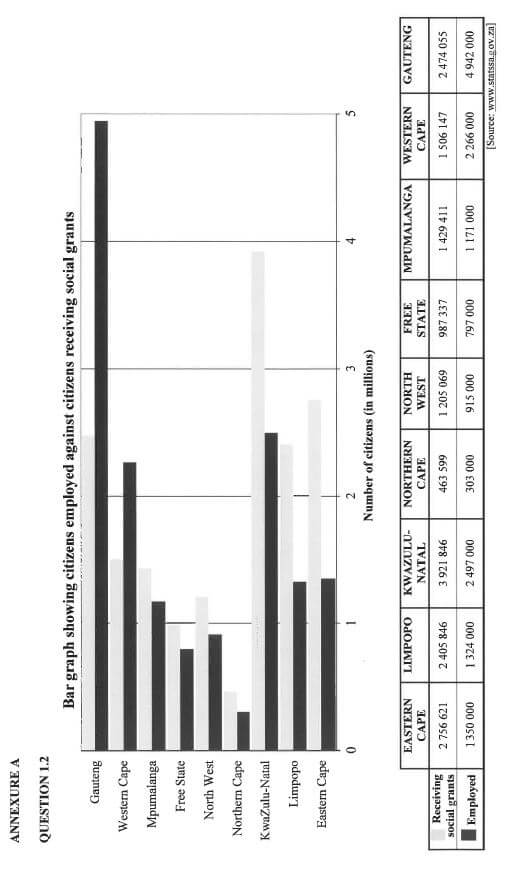
| The South African government offers social support to its citizens by providing social grants to qualifying citizens. The bar graph and table on ANNEXURE A shows the number of citizens who receive social grants and the number of citizens employed per province. |
Use the information on ANNEXURE A to answer the questions that follow.
1.2.1 Identify the province with the second highest number of citizens receiving social grants. (2)
1.2.2 Give ONE reason why governments usually provide grants to some of their citizens. (2)
1.2.3 State, giving a reason, whether the data in ANNEXURE A could also easily be represented using a single pie chart. (3)
1.2.4 Calculate the percentage of citizens receiving social grants in Limpopo. (6)
1.2.5 Gauteng and the Western Cape are the only TWO provinces with more employed citizens than the number of citizens receiving social grants. Determine, using unit ratios, which ONE of these two provinces have more employed citizens than citizens receiving social grants. (6) [37]
QUESTION 2
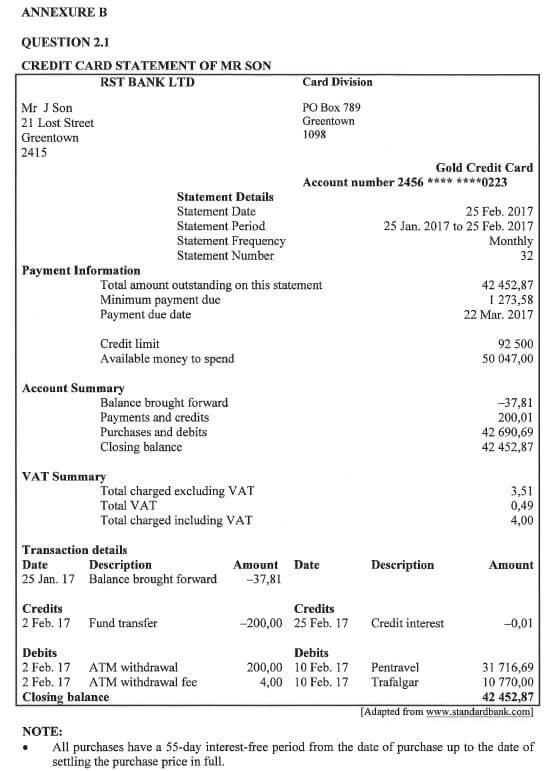
2.1 ANNEXURE B shows the credit card statement of Mr Son.
Use the information in ANNEXURE B to answer the questions that follow.
2.1.1 Determine the number of days covered by this credit card statement. (2)
2.1.2 Use the transaction details and show, with calculations, how the closing balance was determined. (5)
2.1.3 Explain why the bank omitted some digits from the account number on the statement. (2)
2.1.4 The bank offers an insurance option on the outstanding balance of the credit card account by charging a rate of R3,50 per R1 000 (or part thereof) on the outstanding balance. Calculate how much Mr Son would have paid for insurance on the outstanding balance of this statement if he had chosen this option. (5)
2.1.5 Interpret the amount for balance brought forward for this statement. (2)
2.1.6 Give ONE possible reason why Mr Son might purchase goods using his credit card instead of paying cash for the goods. (2)
2.2
| Mr Son travelled from his home directly to a bank 34 km away. He travelled at an average speed of 85 km per hour and arrived at the bank at 12:10. |
Verify, showing ALL calculations, whether Mr Son left his home at exactly 11:40. The following formula may be used:
Distance = average speed x time (5)
2.3 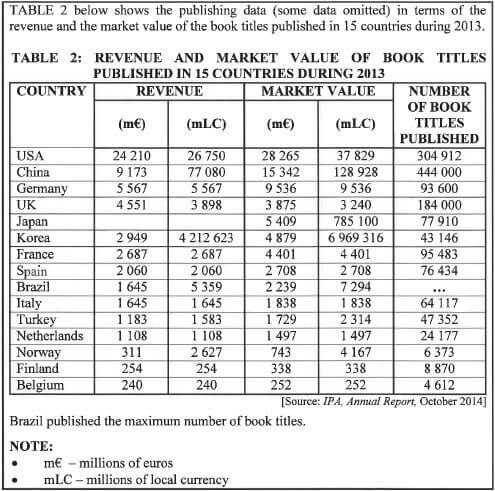
Use TABLE 2 above to answer the questions that follow.
2.3.1 Give ONE possible reason why there is no recorded revenue data for Japan. (2)
2.3.2 Calculate the number of book titles published for Brazil if the range of the number of book titles published is 463 223. (3)
2.3.3 Calculate the median number of book titles published. (4)
2.3.4 Determine the modal market value in euros (€). (2)
2.3.5 Determine the number of countries where the euro (€) is the local currency. (3)
2.3.6 Calculate, as a percentage, the probability of randomly selecting a country whose market value of the published book titles is more than 1 billion euro. (3) [40]
QUESTION 3
3.1
An organiser of a science fair has to produce rectangular display boards. The external dimensions of each board are 48 inches by 36 inches. The front surfaces of the boards must be spray-painted with one layer of non-reflective white paint.
|
Determine, showing ALL calculations, whether 5 litres of the paint would be enough to spray paint 25 display boards. The following formula may be used: Area = length x width (10)
3.2
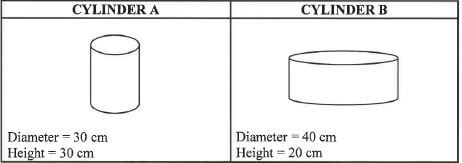
The organiser of the science fair has a choice of two cylindrical containers ( as shown below) for display purposes. A decorative label with a 1 cm overlap will be placed right around the container completely covering the curved surface only. |
Verify, showing ALL calculations, whether cylinder B would require less material to make the decorative labels.
The following formula may be used:
Curved surface area of cylinder = n x diameter x height, where it = 3,142 (7)
3.3
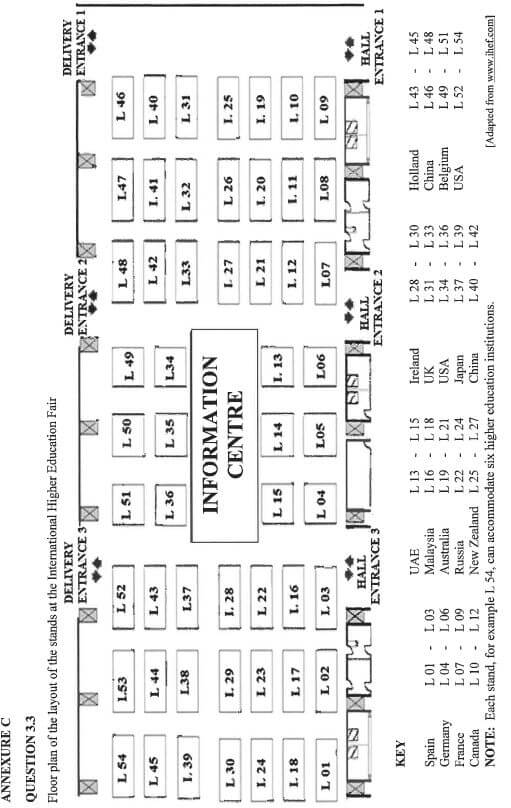
| ANNEXURE C shows the floor plan of the layout of the exhibition stands allocated to countries for the International Higher Education Fair. |
Use ANNEXURE C to answer the questions that follow.
3.3.1 Give ONE practical reason why the information centre is situated in the middle. (2)
3.3.2 Determine the maximum number of higher education institutions from the USA that can exhibit at this fair. (3)
3.3.3 The organisers of the fair identified the most outstanding exhibition stand. Determine the probability that this outstanding exhibition stand will NOT be a stand from China. (3)
3.3.4 An electrician was called to attend to a technical issue at one of the exhibition stands. He followed the route listed below.
- He entered through one of the delivery entrances.
- He proceeded straight ahead passing the information centre on his left-hand side.
- He turned right between the last two rows of stands.
- He then continued straight ahead towards the last stand on his left-hand side to attend to the technical issue.
Identify the delivery entrance used by the electrician and the stand number with the technical issue. (4)
3.3.5 Identify which Chinese stand is closest to the information centre. (2)
3.3.6 Calculate, using measurement, the scale of the floor plan of the layout of the exhibition stands if the actual length of the rectangular information centre is 24,5 m. (5) [36]
QUESTION 4
Ms Bobby decided to open a business that sells sportsware sets with printed school logos. [Adapted from www.bidorbm .co.za] |
Use the information above to answer the questions that follow.
4.1.1 The formula to calculate her total cost is as follows:
Total cost = R10 000 + R105 x (number of sportsware sets)
- Show how the R105 in the formula above was determined. (3)
- Calculate her total cost for 500 sets of sportsware. (2)
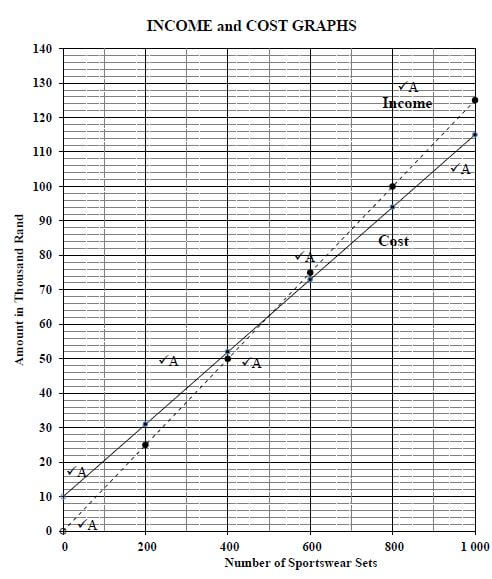
4.1.2 TABLE 3 below shows the relationship between the number of sets of sportsware sold and her total income for the sets.
TABLE 3: NUMBER OF SPORTSWARE SETS SOLD AND THE TOTAL INCOME (in thousand rand)
| NUMBER OF SPORTSWARE SETS SOLD | 0 | 200 | 400 | 500 | A | 800 | 1 000 |
| TOTAL INCOME (in thousand rand) | 0 | 25 | 50 | 62,5 | 87,5 | B | 125 |
Determine the missing values A and B. (6)
4.1.3 Use TABLE 3 and the equation in QUESTION 4.1.1 above to draw TWO straight-line graphs representing the total cost and total income for up to 1 000 sets of sportswear.
Draw clearly labelled graphs on the grid provided on the ANSWER SHEET. (7)
4.1.4
- Write down the number of sportsware sets that must be sold to break even and give the income at the break-even point. (2)
- Determine exactly how many sets of sportsware must be sold to make a profit of R6 000. (3)
4.2 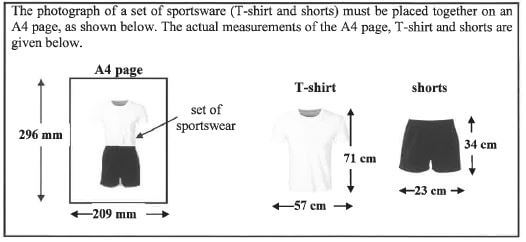
Determine, showing ALL calculations, which ONE of the two scales (1 : 3 or 1 : 4) should be used so that the set of sportsware fits on the A4 page. (6)
4.3
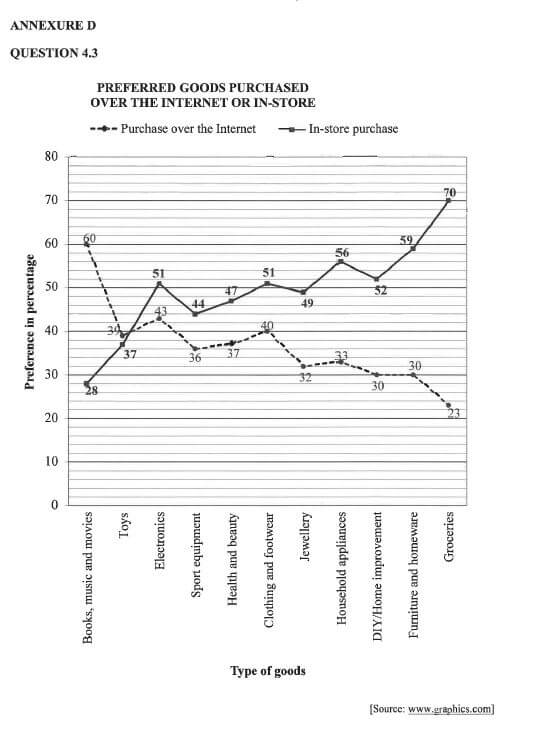
| Ms Bobby is interested in selling her sets of sportsware over the Internet. The line graphs in ANNEXURE D show preferred goods purchased over the Internet and in-store. |
Use ANNEXURE D to answer the questions that follow.
4.3.1 Give ONE possible reason why some people prefer to buy goods over the Internet rather than in-store. (2)
4.3.2 Determine, with calculations, which goods have the same percentage difference between Internet and in-store purchases. (3)
4.3.3 Determine, with a reason, which ONE of the goods would rather be purchased in-store than over the Internet. (3) [37]
TOTAL: 150
ANSWER SHEET 1 QUESTION 4.1.3
INCOME AND COST GRAPHS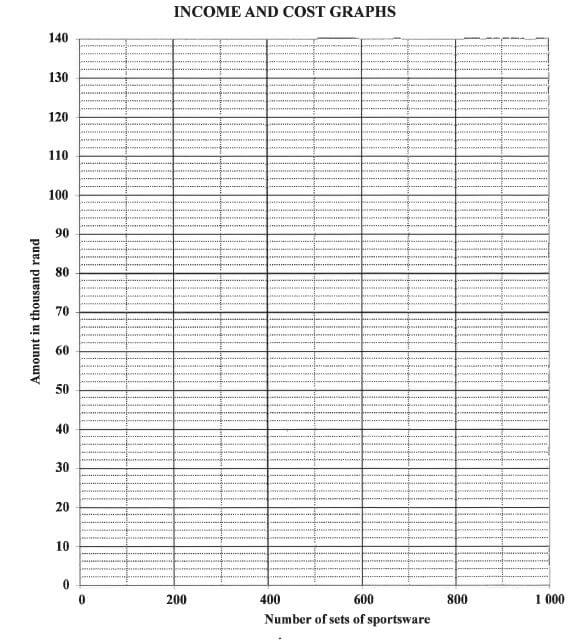
MATHEMATICAL LITERACY PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICAL LITERACY
PAPER 1
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions. Answer ALL the questions.
- Use the ANNEXURES in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 1
- ANNEXURE B for QUESTION 1
- ANNEXURE C for QUESTION 2
- Number the answers correctly according to the numbering system used in this question
- Start EACH question on a NEW
- You may use an approved calculator (non-programmable and non-graphical), unless stated
- Show ALL calculations
- Round off ALL final answers appropriately according to the given context, unless stated
- Indicate units of measurement, where
- Maps and diagrams are NOT necessarily drawn to scale, unless stated
- Write neatly and
QUESTIONS
QUESTION 1
A furniture store offers a dining-room suite for sale. It should be paid off in 42 equal monthly instalments of RI 078,26 (14% VAT included). No deposit is required for this offer. [Source: www rochester.co.za] |
1.1
1.1.1 Express (in years) the total repayment period for this offer. (2)
1.1.2 Determine the total repayment cost for this dining room suite (2)
1.1.3 The advertised price for this dining room suite is R29 999,00. The store offers 15% discount on the advertised price if the purchase is settled immediately in ONE payment
Calculate the value of the discount amount offered. (2)
1.2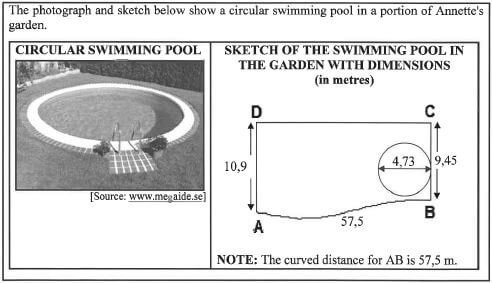
1.2.1 Give, in simplified form, the ratio of distance AD to distance CB (2)
1.2.2 The perimeter of ABCD is 125,92. Calculate the distance CD. (2)
1.2.3 Write down the length of the radius of the pool. (2)
1.2.4 A fence will be erected along the curved side AB at a cost of R97,56 per running metre. Calculate the total cost of erecting the fence. (2)
1.3
TEMPERATURE IN ‘C (Celsius) | WEATHER FORECAST | |||
CITY | MAXIMUM | MINIMUM | SUN AND CLOUD COVER | % CHANCE OF RAIN |
A | 24 | 6 |  | 59 |
32 | 26 | 0 | ||
8 | -7 | 3 | ||
Use TABLE 1 above to answer the questions that follow.
1.3.1 Identify the city with the lowest temperature (2)
1.3.2 Calculate the temperature range for City C (2)
1.3.3 A probability scale in words and as decimal fractions is given below.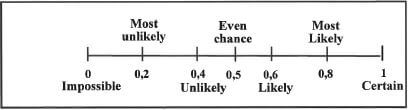
Use the probability scale and TABLE l above to answer the questions that follow.
- Identify the city that has NO chance of rain (2)
- Write down, in words, the chance of rain for City A (2)
1.4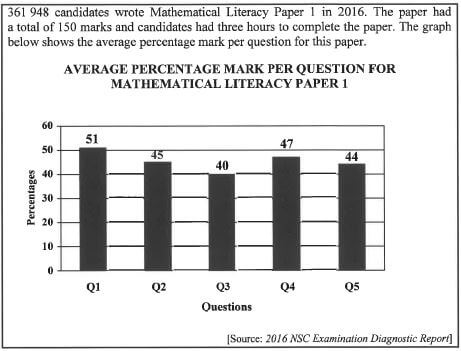
Use the information and the graph above to answer the questions that follow.
1.4.1 Name the type of graph used to represent the data (2)
1.4.2 Express the number of candidates who wrote this paper in words (2)
1.4.3 Identify the question in which the candidates obtained the second lowest average percentage mark (2)
1.4.4 Determine (in minutes) the average time per mark required for this paper (2) [30]
QUESTION 2
2.1
| Mapotjo contributes a regular monthly amount from her salary towards a retirement annuity. This amount is deducted from her salary through a stop order on the 15th day of each month. Below is a summary of the statement of her retirement annuity, as on 10 May 2017. | |
Policy number | 0097541 |
Maturity date | 1 November 2029 |
Monthly contribution | R740,22 |
Payment frequency | Monthly |
Current death value | R189 817,05 |
Retirement value — Lower inflation rate | R536 523,25 |
Retirement value — Higher inflation rate | R940 465,89 |
[Source: www.mv portfolio. co.za | |
Use the information above to answer the questions that follow.
2.1.1 Define the concept stop order (2)
2.1.2 Calculate the difference between the TWO retirement values (2)
2.1.3 Determine the number of monthly contributions that still need to be paid by Mapo{jo before the policy matures (4)
2.1.4 Determine the total value of the contributions over five years if her monthly contribution remains the same (3)
2.1.5 Fill in the missing word(s) to make the following statement TRUE. An annual increase in the monthly contribution would result in ....... maturity value. (2)
2.1.6 Show that if her monthly contribution increased by 8,5%, then the new monthly deduction from her salary would be R803,14. (2)
2.2
| Zoom Car Wash employs a supervisor, eight general cleaners and a machine operator. The cleaners work for seven days a week, where Monday to Saturday is regarded as normal working hours. TABLE 2 below shows the hourly wage rate for EACH of the worker groups for 2016 and 2017. TABLE 2: ZOOM CAR WASH NORMAL HOURLY WAGE RATE (IN RAND PER HOUR) FOR 2016 AND 2017 | ||
WORKER GROUP | 2016 | 2017 |
Supervisor | A | 21,93 |
General cleaners | 16,40 | 17,76 |
Machine operator | 17,90 | 19,39 |
[Adapted from Mvwaee co za] | ||
NOTE:
| ||
Use TABLE 2 above to answer the questions that follow.
2.2.1 Calculate the 2017 overtime hourly rate for a general cleaner (2)
2.2.2 Determine the total wage a machine operator would earn for working only THREE Sundays (5)
2.2.3 All the workers received a wage increase at the beginning of 2017
- Show, by calculation, that the wage increase was 8,3%. (2)
- Calculate the missing value A (3)
2.2.4 A general cleaner worked normal working hours for a full week. Calculate his total weekly wage. (3)
2.3 TABLE 3 below shows the record of the vehicles washed on a particular day.
| TABLE 3: RECORD OF VEHICLES WASHED ON A PARTICULAR DAY | ||
CATEGORY | NUMBER | COST PER VEHICLE |
Bakkies | 7 | R70 |
Cars | 35 | R50 |
Minibus | 4 | R75 |
Calculate the total income received for the vehicles washed on this particular day. (4)
2.4
| The supervisor at Zoom Car Wash has to report for duty 30 mminutes earlier than the normal starting time, from Monday to Saturday but leaves work at the same time as the other workers. He receives a monthly salary, works every Sunday and is paid overtime. TABLE 4 below shows a monthly salary slip (some data omitted) for the supervisor. TABLE 4: MONTHLY SALARY SLIP FOR THE SUPERVISOR | |||
SALARY SLIP | |||
Name of employer | Zoom Car Wash | ||
Address | 12 Stateway | ||
Name of employee | M Ncubuka | ||
ID No.: 890106 5387 000 | Employee No.: 124567 | ||
Position | Supervisor | ||
Payment period: 1 November 2017 to 30 November 2017 | |||
RATE | TOTAL HOURS | AMOUNT IN | |
Normal hours worked | 21,93 | ...... | B |
Sunday hours (1,5 normal rate) | 32,90 | 9 × 1 × 4 | 1 184,40 |
Overtime hours worked/ (1}— of normal rate) | ...... | 0,5 × 6 × 4 | 350,88 |
TOTAL Gross Salary | 6 272,16 | ||
UIF (1% of gross salary) | .... | ||
Net salary | 6 209,44 | ||
[Source: www.zoomhandcarwash.com] NOTE: Employer and employee each contribute a monthly amount of 1% of the employee's gross salary for UIF. | |||
Use TABLE 4 above to answer the questions that follow.
2.4.1 Explain the term employer (2)
2.4.2 State ONE benefit of contributing towards the UIF (2)
2.4.3 Calculate:
- The value of B (3)
- The total UIF amount that must be paid on behalf of M Ncubuka to the Department of Labour (3) [44]
QUESTION 3
3.1
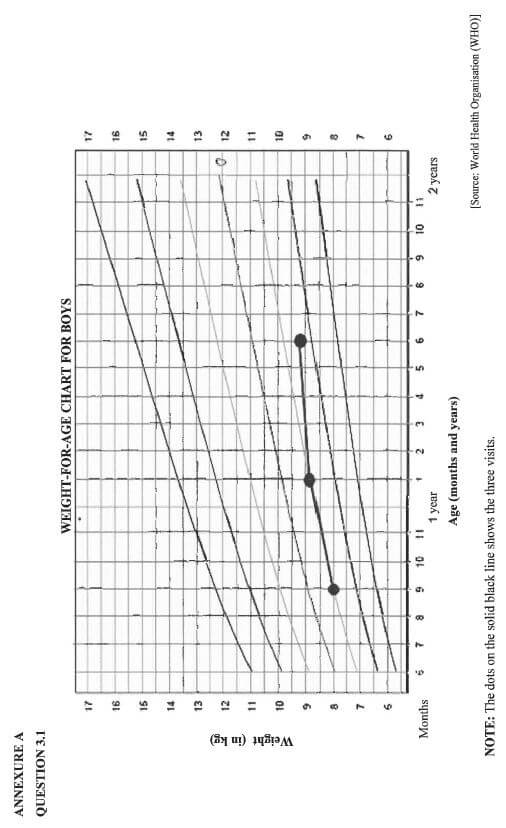
| A nurse from Port Allen Clinic conducts road shows to demonstrate the use of growth charts to parents. She uses a weight-for-age chart for boys as on ANNEXURE A, which shows the recorded measurements of a boy for three visits. |
Use ANNEXURE A to answer the questions that follow.
3.1.1 Identify the age group represented on this chart (2)
3.1.2 Give the boy's weight at his first visit (2)
3.1.3 Determine the boy's age (in months) during a visit when he weighed a little less than 9 Kg (2)
3.1.4 The boy's first visit was in May.Determine the month in which the third visit took place. (2)
3.1.5 During the fourth visit, the boy weighed 11,2 kg and his body mass index (BMI) was calculated as 19,5 kg/m2. Calculate the boy's corresponding height (in metres) rounded off to THREE decimal places. (4)
You may use the following formula: BMI = weight (in kg)
(height in m) 2
3.2
The nurse uses a sedan vehicle to travel. The fuel consumption of her vehicle is 7,6 litres per 100 km travelling at an average speed. [Adapted from m.automobilio.info] |
3.2.1 Calculate (to the nearest km) the distance her vehicle can travel using 55 litres of petrol (3)
3.2.2 The nurse spends 1 hour and 45 minutes on a particular day driving between two workstations that are 189 km apart. Determine the average speed of the vehicles. (3)
You may use the following formula: Average speed = distance
time
3.3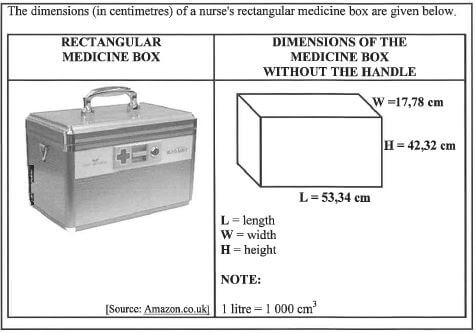
3.3.1 Calculate the volume (to the nearest litre) of ONE medicine box excluding the handle. (4)
You may use the following formula:
Volume = length × width × height
3.3.2 The medicine box contains FOUR identical smaller boxes. EACH small box contains four different types of pills in cylindrical containers which are labelled A, B, K and U, as shown below
Determine (as a decimal fraction) the probability of randomly selecting a type U container from the medicine box. (3) [25]
QUESTION 4
4.1
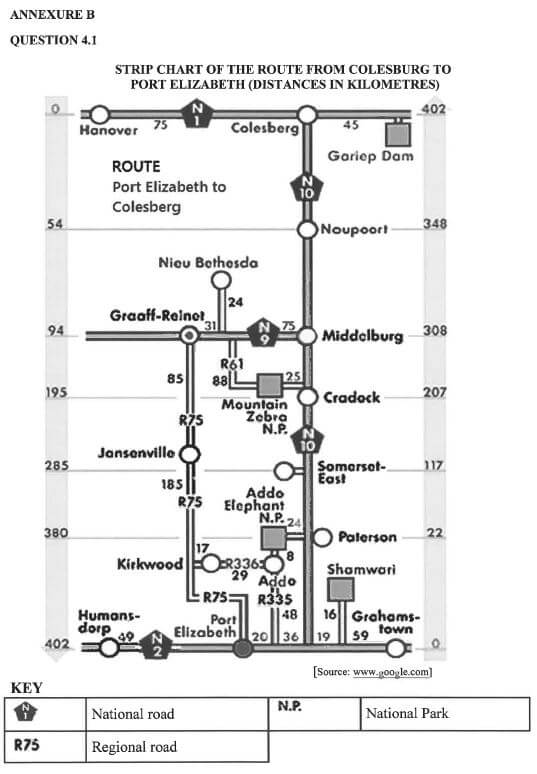
Rammone plans to travel from Colesberg to Port Elizabeth using only national roads. |
Use ANNEXURE B to answer the questions that follow.
4.1.1 .Name the national roads that Rammone will use to travel to Port Elizabeth (2)
4.1.2 Which national park is furthest from the N10? (2)
4.1.3 Rammone met a friend in Paterson who had to travel 61 km via the R336 from his hometown. Name the friend's hometown. (2)
4.1.4 Calculate the travel distance between the TWO national parks(3)
4.2
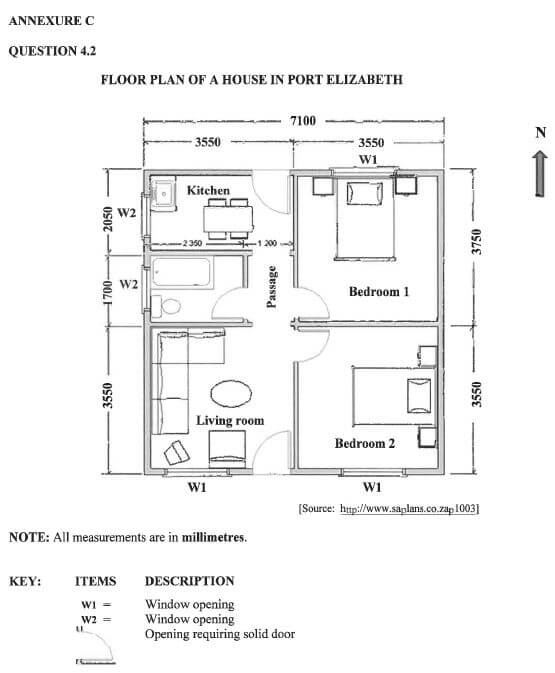
Rammone visited Port Elizabeth to check on the progress made on the house being built for his parents. |
Use ANNEXURE C to answer the questions that follow.
4.2.1 Give (in mm) the external length of the wall that makes the area of Bedroom 1 larger than Bedroom 2 (2)
4.2.2 Determine (in m) the total external length of the western wall of the house (2)
4.2.3 Name the room(s) that has more than ONE entrance (2)
4.2.4 Identify the roorrr that has the same floor area as the living room (2)
4.2.5 Which bathroom fixture is NOT shown on the floor plan? (2) [19]
QUESTION 5
5.1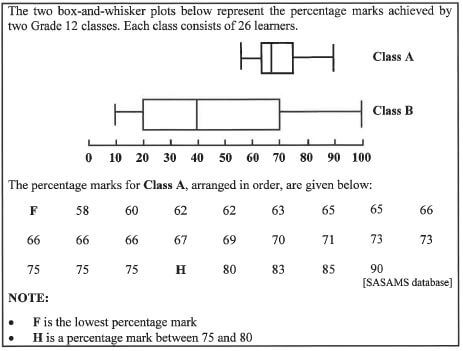
5.1.1 Which ONE of the following terms best describes the data above:
- Categorical
- Numerical
- Qualitative (2)
5.1.2 Determine the percentage of data values that lies between the upper and lower quartiles (2)
5.1.3 The range of Class A is 34. Calculate the value of F. (3)
5.1.4 Calculate the median percentage mark for Class A (2)
5.1.5 Determine the inter quartile range for Class B (3)
5.1.6 Give the modal percentage mark for Class A (2)
5.1.7 Calculate the missing value H if the mean percentage mark for Class A is 70%. (3)
5.1.8 Determine (as a simplified common fraction) the probability of randomly selecting a learner from Class A who obtained a percentage mark different from any other learner in the class (3)
5.2
| A survey on the distribution of literacy levels among adults aged 35 to 64 was conducted in all provinces in South Africa. Table 5 below shows the 2016 adults (aged 35 to 64) literacy levels per province. TABLE 5: ADULTY (AGED 35 TO 64) LITERACY LEVELS PER PROVINCE | |||||
PROVINCE | LITERACY LEVELS | TOTAL | |||
NON-LITERATE | LITERATE | ||||
Number | % | Number | % | ||
Western Cape | 288 918 | 14,1 | 1 762 494 | 85,9 | 2 051 412 |
Eastern Cape | 393 954 | 26,0 | 1 120 567 | 74,0 | 1 514 521 |
Northern Cape | 94 552 | 27,9 | 244 282 | 72,1 | 338 834 |
Free State | 192 933 | 24,1 | 609 029 | 75,9 | 801 962 |
KwaZulu-Natal | 650 033 | 24,9 | 1 956 497 | 75,1 | 2 606 530 |
North West | 299 994 | 28,3 | 760 068 | 71,7 | 1 060 062 |
Gauteng | 575 371 | 12,5 | 4 013 463 | 87,5 | 4 588 834 |
Mpumalanga | 312 273 | 28,5 | 784 347 | 71,5 | 1 096 620 |
Limpopo | 372 090 | 28,7 | 922 171 | 71,3 | 1 294 261 |
TOTAL | Q | 12 172 918 | 15 353 036 | ||
[Adapted from Community Survey, 2016] NOTE: Some data has been omittted. | |||||
Use TABLE 5 above to answer the questions that follow.
5.2.1 Calculate the missing value Q (2)
5.2.2 Determine the percentage of literate adults in South Africa (3)
5.2.3 Express (as a unit ratio) the number of non-literate adults to the number of literate adults in KwaZulu-Natal. (3)
5.2.4 Arrange the number of literate adults per province in ascending order (2)
5.2.5 Determine the province with the smallest difference between the number of literate and the number of non-literate adults (2) [32]
TOTAL: 150
MATHEMATICAL LITERACY PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICAL LITERACY
PAPER 1
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
SYMBOL | EXPLANATION |
M | Method |
MA | Method with accuracy |
CA | Consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
RT/RG | Reading from a table/graph/diagram |
SF | Correct substitution in a formula |
O | Opinion/Example/Definition/Explanation |
P | Penalty, e.g. for no units, incorrect rounding off, etc. |
R | Rounding off |
NPR | No penalty rounding or omitting units |
AO | Answer only, full marks |
MEMORANDUM
Question 1 [30Marks] AO | |||||
Ques | Solution | Explanation | Topic/L | ||
1.1.1 | 3½ years ✔✔ A | 2A numerical period |
(2) | M | |
1.1.2 | Total Repayment Cost = R1 078,26 × 42 ✔ M/A | 1MA multiply term by instalment |
(2) | F | |
1.1.3 | ✔M | 1M calc. discount | (2) | F | |
1.2.1 | AD : CB = 10,9 : 9,45 ✔M | 1M ratio form (1: 0,87) OR (1,15 : 1) | (2) | MP | |
1.2.2 | ✔M/A | 1M/A subtracting all lengths | (2) | M | |
1.2.3 | Radius = 4,73 m ✔ M | 1M dividing by 2 | (2) | M | |
1.2.4 | ✔M/A | 1M/A multiply cost by correct distance | (2) | F | |
1.3.1 | C ✔✔A | 2A city | (2) | D | |
1.3.2 | Range = 8oC – (– 7oC)✔MA | 1MA subtracting correct values | (2) | D | |
Ques | Solution | Explanation | Topic/L | ||
1.3.3 (a) | B ✔✔A | 2A city | (2) | P | |
1.3.3 (b) | Likely OR less likely ✔✔A | 2A correct words | (2) | P | |
1.4.1 | Bar graph ✔✔A | 2A correct type | (2) | D | |
1.4.2 | ✔✔A | 2A number in words | (2) | M | |
1.4.3 | Q 5 ✔✔A | 2A correct question | (2) | D | |
1.4.4 | Average time per mark = 180 min ✔MA | 1MA numerator and denominator | (2) | D | |
[30] | |||||
Question 2 [44 Marks] | |||
Ques | Solution | Explanation | Topic/L |
2.1.1 | Stop order: an instruction to an employer or bank to pay / divert monthly or transfer regularly a certain amount to a person or an account. ✔✔O | 2O explanation (2) | F |
2.1.2 | ✔ M/A | 1M/A subtraction of correct value | F |
2.1.3 | Number of years (2017 – 2029) = 12 ✔ M/A | 1M/A calculating years | F |
2.1.4 | Total contribution value | 1M/A multiplying (5 and 12) | F |
2.1.5 | ✔✔A | 2A correct missing words (2) | F |
Ques | Solution | Explanation | Topic/L |
2.1.6 | ✔MA | 1MA percentage | F |
2.2.1 | Hourly overtime rate = R17,76 ×11/3 ✔MA | 1MA hours | F |
2.2.2 | ✔MA ✔A | 1MA increasing by 150% | F |
Ques | Solution | Explanation | Topic/L |
2.2.3 (a) | ✔A % increase = 17,76 -16,40 × 100% ✔M | 1M percentage | F |
2.2.3 (b) | A × 108,3% = 21,93 ✔RT | 1RT reading values | F |
Ques | Solution | Explanation | Topic/L |
2.2.4 | 2017 | 1RT reading value from the table | F |
2.3 | Total Income for the day | 2RT correct values | F |
Ques | Solution | Explanation | Topic/L |
2.4.1 | Employer provides people job/work for pay | 2O explanation (2) | F |
2.4.2 | ✔O ✔O | 2O reason (2) | F |
2.4.3(a) | ✔ RT ✔M | 1RT amounts |
F |
2.4.3 (b) | 1% of gross salary = R6 272,16 – R6 209,44 ✔MA | 1MA subtracting correct values | F |
[44] |
QUESTION 3 [25 MARKS] | |||
Ques | Solution | Explanation | Topic/L |
3.1.1 | ✔RT ✔RT ✔RT ✔RT | 2RT age | M |
3.1.2 | 8 kg ✔✔RT | 2RT mass/weight (2) | M |
3.1.3 | 12 months to 15 months ✔✔ RT | 2RT (one age in this range) (2) | M |
3.1.4 | February ✔✔A | 2Acorrect month (2) | M |
3.1.5 | BMI = weight (in kg) | 1SF correct values | M |
3.2.1 | Distance = 55 litre × 100 km ✔ MA | 1MA multiply by 100 | M L2 |
3.2.2 | ✔ SF Average speed = 189 = 189 | 1C to hours | M |
3.3.1 | ✔ SF | 1SF correct substitution | M |
3.3.2 | P(U)= 3 12 ✔ A | 1A numerator | P |
[25] | |||
QUESTION 4 [19 MARKS] | |||||
Ques | Solution | Explanation | Topic/L | ||
4.1.1 | ✔ A ✔ A | 1A N10 | (2) | MP | |
4.1.2 | ✔✔ RT | 2RTcorrect name | (2) | MP | |
4.1.3 | Kirkwood ✔✔A | 2A correct hometown | (2) | MP | |
4.1.4 | ✔RT ✔ M | 1RT correct distances 1M adding | (3) | MP L2 | |
4.2.1 | 3750 mm ✔✔ A | 2A distance | (2) | MP | |
4.2.2 | = 3 550 mm + 3750 mm✔A | 1A adding 3 correct distances | (2) | MP | |
4.2.3 | Living room. ✔✔ A | 2A | (2) | MP | |
4.2.4 | Bedroom 2 ✔✔A | 2A room | (2) | MP | |
4.2.5 | Wash basin/sink/water basin OR Shower ✔✔ A | 2A any item | (2) | MP | |
[19] | |||||
QUESTION 5 [32MARKS] | |||||
Ques | Solution | Explanation | Topic/L | ||
5.1.1 | Numerical ✔✔A | 2A answer | (2) | D | |
5.1.2 | 50% ✔✔A | 2A answer | (2) | D | |
5.1.3 | Range = Maximum - minimum ✔M | 1M range concept (can be implied)
| (3) | D | |
5.1.4 | Median % = 67 + 69 ?M | 1M concept of median | (2) | D | |
5.1.5 | Inter-quartile range = Q3 - Q1 ✔M | 1M IQR concept(implied) | (3) | D | |
5.1.6 | 66 ??A | 2A mode | (2) | D | |
| 5.1.7 | Mean = sum of the marks | 1MA mean concept (implied) 1A adding values 1CA value of H | (3) | D | |
5.1.8 | P (equal marks) = 13 ?A | 1A numerator | (3) | P | |
Ques | Solution | Explanation | Topic/L |
5.2.1 | ?MA | 1MA adding all Non- literate adults | D L1 |
5.2.2 | ? RT | 1RT numerator and denominator 1M multiply by 100 1CA answer | D |
5.2.3 | Non Literate: Literacy = 650 033:1 956 497? RT = 650 033 : 1956 497 ?MA 650 033 650 033 = 1 : 3,009842577 ≈1 : 3 or 1 : 3,01 or 1 : 3,0099 ? CA | 1RT both values | D |
5.2.4 | ??MA 244 282; 609 029; 760 029;784 347; 922 171; 1 120 567; 1 762 494; 1 956 497; 4 013 463 | 2MA arranging (2) | D |
5.2.5 | Northern Cape (NC) ??A | 2A correct province (2) | D |
[32] | |||
TOTAL: | 150 |
MATHEMATICAL LITERACY PAPER 2 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
MATHEMATICAL LITERACY
PAPER 2
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
SYMBOL | EXPLANATION |
M | Method |
MA | Method with accuracy |
CA | Consistent accuracy |
RCA | Rounding consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
RT/RG | Reading from a table/graph/diagram |
SF | Correct substitution in a formula |
O | Opinion/Example/Definition/Explanation/Justification/Verification |
P | Penalty, e.g. for no units, incorrect rounding off, etc. |
R | Rounding off |
NPR | No penalty rounding or omitting units |
AO | Answer only, full marks |
MEMORANDUM
QUESTION 1 [37 MARKS] | |||
Ques | Solution | Explanation | T/L |
1.1.1 | Number of days = 10 ✔A | 1A 10 days | M |
1.1.2 | VAT on teens ticket Price without VAT = R50 or R50 | 1RT using correct value OR 1RT using correct value | F |
1.1.3 | ✔(A | 1A numerator | P |
Ques | Solution | Explanation | T/L |
1.1.4 | For 23 April: For 20 April: Mrs Abrahams statement is VALID ✔O OR For 23 April: For 20 April: | 1RT all correct values OR 1RT all correct values | F |
1.2.1 | Eastern Cape or EC ✔✔RT | 2RT correct province (2) | Data |
Ques | Solution | Explanation | T/L |
1.2.2 | Supporting the needy /poor / sick / elderly / orphaned ✔✔O | 2O reason (2) | Data |
1.2.3 | ✔✔O OR | 1O opinion | Data |
1.2.4 | Total number of citizens receiving social grants = ✔M ≈ 14 ,028313 % ✔ CA Limpopo percentage | 1M adding | Data |
Ques | Solution | Explanation | Topic/L |
1.2.5 | Gauteng Western Cape Western Cape ✔RT | 1M writing as a ratio | Data |
[37] |
QUESTION 2 [40 MARKS] | |||
Ques | Solution | Explanation | T/L |
2.1.1 | 32 OR 31 v'v'A | 2A correct number of days (2) | M L2 |
2.1.2 | Total credit ✔MA ✔MA | 1MA adding credits [Using the Account Summary: Closing Balance max 4 marks] (5) | F L3 |
2.1.3 | ✔✔O | 2O Explanation (2) | F L4 |
2.1.4 | Insurance premium Insurance cost | 1M dividing by 1 000 | F |
Ques | Solution | Explanation | Marks | T/L |
2.1.5 | The bank owes Mr Son R 37,81 ✔✔O | 2Oreason | (2) | F |
2.1.6 | Does not have large amounts of cash to purchase expensive goods ✔✔O | 2O reason | (2) | F L4 |
Ques | Solution | Explanation | T/L |
2.2 | Distance = average speed × time ✔SF | 1SF substitution of both values | M |
2.3.1 | No data was available for Japan ✔✔O | 2O no data available (2) | Data |
2.3.2 | Range = maximum – minimum I ✔M | 1M range concept | Data |
2.3.3 | ✔MA | CA from2.3.2 | Data |
2.3.4 | no mode ✔✔A | 2A no mode (2) | Data |
Ques | Solution | Explanation | T/L |
2.3.5 | 7 countries ✔✔✔A | 3A correct number of countries | Data |
2.3.6 | ✔A | 1A numerator | Prob. |
[40] |
QUESTION 3 [36 MARKS] | |||
Ques | Solution | Explanation | T/L |
3.1 | Area of display = length x width = 48 inches x 36 inches ✔SF | 1SF substituting correct values
| M |
Ques | Solution | Explanation | T/L |
3.2 | Total Surface Area of cylinder A | 1SF correct values [Max 5 marks if the overlap is left out] (7) | M L4 |
Ques | Solution | Explanation | T/L |
3.3.1 | Easily accessible to all stands ✔✔R | 2R reason (2) | Maps L4 |
3.3.2 | Maximum number of HEI from the USA | 1M multiplying by 6 | Maps L2 |
3.3.3 | ✔A | 1A numerator | P L2 |
3.3.4 | Delivery entrance 3 ✔✔A | 2A Delivery entrance | Maps L3 |
3.3.5 | L 42 ✔✔A | 2A stand number (2) | Maps L2 |
Ques | Solution | Explanation | T/L |
3.3.6 | ✔A | 1A measuring with ruler (Accept a range of 66 74; dependant on provincial printing) | Maps L3 |
[36] |
QUESTION 4 [37 MARKS] | |||
Ques | Solution | Explanation | T/L |
4.1.1 (a) | R105 = cost of T-shirt + cost of Shorts + printing | 1A cost of T-shirt | F L2 |
4.1.1 (b) | ✔SF | 1SF substitution [Using the selling price 0 marks] (2) | F L2 |
4.1.2 | 87,5 thousand rand = R87 500 ✔A B = 800 × 125 ✔M | 1A writing value in full | F L2 |
Ques | Solution | Explanation | T/L |
4.1.3 |
| F L3 (7) | |
Ques | Solution | Explanation | Topic/L |
4.1.4 (a) | Number of Sets = 500 ✔CA | 1CA number of sets [Accept values between R62 000 to R63 000] (2) | F L3 |
4.1.4 (b) | Number of sets = 800 ✔✔✔RT | 3RT number of sets from graph (CA from graph) | F L3 |
Ques | Solution | Explanation | T/L |
4.2 | For Scale: 1 : 3 | 1M adding lengths | Maps L4 |
4.3.1 | Convenient ✔✔O Cheaper ✔✔O | 2O reason (2) | F L4 |
Ques | Solution | Explanation | Topic/L |
4.3.2 | ✔A | 1A Electronics | F L2 |
4.3.3 | Groceries ✔A | 1A Item | F L4 |
[37] | |||
TOTAL: 150 |
RELIGIOUS STUDIES PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
RELIGIOUS STUDIES
PAPER 2
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions.
- Answer any THREE questions.
- Start EACH question on a NEW page.
- Read ALL the questions carefully.
- Number the answers correctly according to the numbering system used in this question paper.
- The length of your answers must be in accordance with the marks allocated to each question.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Read the statement below and answer the questions that follow.
There are many religions in the world, each with its own identity. However, within any one religion, there are bound to be some differences. Sometimes these differences are minor, and at other times they spill over into open warfare. |
1.1.1 Name the major sects or branches of any ONE religion. (6)
1.1.2 Compare the religious BELIEFS of the various branches of the religion you have selected. (14)
1.1.3 Elaborate on the different ways in which religions deal with their internal differences. Give examples to illustrate your answer. (14)
1.2 In terms of CENTRAL TEACHINGS of any ONE religion, discuss the place and responsibility of humanity in the world. (16) [50]
QUESTION 2
2.1 Discuss the relationship between oral tradition and sacred text. Use examples from AT LEAST TWO religions to illustrate your answer. (20)
2.2 Read the statement below and answer the questions that follow.
| In 1859 Charles Darwin published a book titled, On the Origin of Species. In this book he argued that all living things change over time, to adapt to changing environments. |
2.2.1 Explain why certain religions objected strongly to Darwin's teachings. (16)
2.2.2 Explain the reasons for the popularity of Darwin's theory in modern day society. (14) [50]
QUESTION 3
Read the following extract and answer the questions that follow.
Of course, not all religious conflicts are wars: sometimes the conflict is only verbal, and does not involve any violence. Sometimes conflicts simmer for many years. And at other times conflict spills over into open war. [Source: Adapted from Religion Studies, Steyn et al. p. 229] |
3.1 Select a recent armed conflict in any ONE of the following geographical regions (A–C), and answer the questions that follow.
A Europe
B Middle East
C Asia
3.1.1 State the region selected (A, B or C). Then name the country and warring groups. (6)
3.1.2 Explain the causes of the conflict (include both religious and other causes). (20)
3.1.3 What is the present situation in the conflict area? (8) 3.2 Religious conflicts throughout the world are decreasing. Do you agree with this statement? Give reasons for your answer. Use TWO examples to illustrate your answer. (16) [50]
QUESTION 4
4.1 What do you understand by the term world view? (4)
4.2 Name ANY TWO secular world views and explain the beliefs of each. (10 x 2) (20)
4.3 What is the impact of secularism on society? (14)
4.4 List and explain any THREE hermeneutical principles. (12) [50]
QUESTION 5
Read the extract below and answer the questions that follow.
BEACH BULLIES RANT* ON SOCIAL MEDIA Social media is a convenient platform on which people can display their discriminatory attitudes. Holidays are exceptionally vocal times for racists on Facebook and Twitter who cannot stand the sight of black people enjoying some sand and surf. [Source: Adapted from News24.com. Accessed on 10 January 2017.] |
5.1 Explain the concept discrimination and use THREE examples to illustrate your answer. (12)
5.2 Analyse the impact of discrimination on society. (10)
5.3 With reference to any ONE religion, discuss the teachings that specifically address the problem of discrimination. (18)
5.4 What practical strategies can religious organisations implement to combat discrimination in our society? (10) [50]
TOTAL: 150
RELIGIOUS STUDIES PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
RELIGIOUS STUDIES
PAPER 1
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of SECTION A and SECTION B.
- SECTION A: COMPULSORY
SECTION B: Answer any TWO questions in this section. - Read ALL the questions carefully.
- Start EACH question on a NEW page.
- The length of your answers must be in accordance with the marks allocated to each question.
- Number the answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
QUESTIONS
SECTION A (COMPULSORY)
QUESTION 1
1.1 Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question number (1.1.1–1.1.10) in the ANSWER BOOK, for example 1.1.11 D.
1.1.1 A feeling of connection to the divine:
A Conciliatory
B Communion
C Compassion
D Confirmed (1)
1.1.2 Sangha is believed to be one of the three jewels of …
A Buddhism.
B the New Age Movement.
C Hinduism.
D the Bahá'i faith. (1)
1.1.3 Ecumenical is …
A bread that is eaten at Christian rituals.
B a Jew.
C any person who is NOT a Jew.
D promoting unity among Christians. (1)
1.1.4 According to its teachings, all religions are part of God 's divine plan for humanity:
A Islam
B Bahá'i faith
C Christianity
D Taoism (1)
1.1.5 The holy book of Buddhism is the …
A Ketuvim.
B Mahabharata.
C Tripitaka.
D Neviim. (1)
1.1.6 All religions are paths towards the truth and they are equally true:
A Inclusivism
B Pluralism
C Ideology
D Identity (1)
1.1.7 The followers of this religion believe they are the 'chosen people':
A Christianity
B Bahá'i faith
C Judaism
D Islam (1)
1.1.8 The sacred book of Islam is the …
A Old Testament.
B Torah.
C Qur'an.
D first five books of the Bible. (1)
1.1.9 The following religions communicate with the Supreme Being through intermediaries:
A African Traditional Religion and Islam
B African Traditional Religion and Christianity
C Hinduism and Buddhism
D Judaism and Islam (1)
1.1.10 All world processes are made up of two forces:
A Male and female
B Wane and death
C Diviner and power
D Yin and yang (1)
1.2 Choose a description from COLUMN B that matches the term in COLUMN A. Write only the letter (A–G) next to the question number (1.2.1–1.2.6) in the ANSWER BOOK. Do NOT use any letter more than once.
COLUMN A | COLUMN B |
1.2.1 Buddhism 1.2.2 Lineage 1.2.3 Swami 1.2.4 Ritual 1.2.5 Conviction 1.2.6 Islam |
(6 x 1) (6) |
1.3 Complete the following sentences by filling in the missing word(s). Write only the word(s) next to the question number (1.3.1–1.3.5) in the ANSWER BOOK.
1.3.1 The founding figure of Buddhism was … and he is known as the Buddha. (2)
1.3.2 The Muslim religious leader whose authority is believed to be derived from Prophet Mohammed is the … (2)
1.3.3 In Hindu society, the highest caste is known as the priestly or the … (2)
1.3.4 The Queen of England is the hereditary head of the … Church. (2)
1.3.5 In the African Traditional Religion, the special people that are called by their ancestors to heal the living are called … (2)
1.4 In the context of religion, define the following terms in TWO sentences:
1.4.1 Polytheism (2)
1.4.2 Ideology (2)
1.4.3 Reincarnation (2)
1.4.4 Nirvana (2)
1.4.5 Sect (2)
1.5 Indicate whether each of the following statements is TRUE or FALSE. Give a reason if the statement is false. Write 'true' or 'false' and the reason next to the question number (1.5.1–1.5.5) in the ANSWER BOOK.
1.5.1 Baptism is a spiritual discipline including breath control, simple meditation, and specific body postures. (2)
1.5.2 In the Abrahamic faiths, spontaneity and flexibility are the characteristics of the path that the universe travels. (2)
1.5.3 The Ten Commandments were revealed to Jesus Christ. (2)
1.5.4 The word 'immortal' means living forever or everlasting. (2)
1.5.5 The Book of Mormon is one of the sacred texts for the Bahá'i faith. (2)
1.6 In TWO sentences, briefly describe EACH of the following as they apply to the study of religion:
1.6.1 Doctrine (2)
1.6.2 Myth (2)
TOTAL SECTION A: 50
SECTION B
Answer any TWO questions in this section.
QUESTION 2
2.1 In the context of religion, write ONE fact on EACH of the following terms and give ONE example to illustrate its meaning:
2.1.1 Difference (4)
2.1.2 Teachings (4)
2.1.3 Dharma (4)
2.1.4 Syncretism (4)
2.1.5 Exclusivism (4)
2.2 State any THREE unique features of EACH of the following religions:
2.2.1 Christianity (6)
2.2.2 Taoism (6)
2.2.3 African Traditional Religion (6)
2.3 Discuss the importance of uniqueness in religion. (12) [50]
QUESTION 3
3.1 Read the extract below and answer the questions that follow.
FUNERAL OF A STRUGGLE HERO Professor Jonathan Jansen, Vice-Chancellor of the Free State University, hit the nail on the head with a beautifully written message on Facebook this week. The message pays tribute to Ahmed Kathrada, the struggle hero who passed away this week. Jansen reminds us all of just how unique and amazing South Africa is. [Adapted from http://News 24/ahmedkathrada. Accessed on 30 March 2017] |
3.1.1 What lessons does this message teach us? Give evidence from the extract to support your answer. (12)
3.1.2 Discuss any THREE reasons that, according to the message, make South Africa unique. (12)
3.1.3 The last line of the message reads, 'For a moment, just a moment, it felt good to hope again …' What do you think Jansen means by this? (6)
3.1.4 List THREE advantages and THREE disadvantages of religious organisations using social media. (6 x 2) (12)
3.2 Why do you think the media is generally biased in the coverage of religious issues? (8) [50]
QUESTION 4
4.1 Read the statement below and answer the questions that follow.
INTERRELIGIOUS RELATIONSHIPS PAST AND PRESENT When the white man came to our country, he had the Bible and we had the land. The white man said to us, 'Let us pray.' After the prayer, the white man had the land and we had the Bible. (Dube, MW [2000]. Postcolonial Feminist Interpretation of the Bible [St Louis, Chalice Press]) [Source: Shuters Top Class Religion Studies Grade 12] |
4.1.1 In the context of the statement above, explain colonialism. (4)
4.1.2 Do you agree with Dube's interpretation of missionary work? Give reasons for your answer. (12)
4.1.3 Compare the terms interreligious dialogue and intrareligious dialogue and give ONE example in each case. (8)
4.2 Name ONE organisation that works to promote interreligious relationships in Africa. State any SEVEN of its achievements. (16)
4.3 Briefly discuss the background and main purpose of the organisation you named in QUESTION 4.2. (10) [50]
QUESTION 5
5.1 State any FOUR contributions by the World Conference for Religions for Peace, which promote interreligious harmony. (8)
5.2 With reference to any of the religions you have studied, discuss religious teachings that promote good morality. (10)
5.3 Critically analyse the role religions played in the struggle against apartheid in South Africa. (12)
5.4 Read the following extract and answer the questions that follow:
HUMAN RIGHTS AND RESPONSIBILITIES The concept of human rights has been in existence for centuries. The need to establish an international agreement regarding human rights became urgent at the end of World War II. [Source: Focus on Religion Studies, Grade 12] |
5.4.1 What does the concept of religious freedom imply? (4)
5.4.2 Explain what is meant by human rights. (4)
5.4.3 Explain how different religions are practically involved in promoting religious freedom, human rights and responsibilities. (12) [50]
TOTAL SECTION B: 100
GRAND TOTAL: 150
RELIGIOUS STUDIES PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
RELIGIOUS STUDIES
PAPER 1
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
MEMORANDUM
SECTION A (COMPULSORY)
QUESTION 1
1.1
1.1.1 B √ (1)
1.1.2 A√ (1)
1.1.3 D√ (1)
1.1.4 B√ (1)
1.1.5 C√ (1)
1.1.6 A√ (1)
1.1.7 C√ (1)
1.1.8 C√ (1)
1.1.9 B√ (1)
1.1.10 D√ (1)
1.2
1.2.1 G√ (1)
1.2.2 E√ (1)
1.2.3 D√ (1)
1.2.4 F√ (1)
1.2.5 C√ (1)
1.2.6 A√ (1)
1.3
1.3.1 Siddhartha Gautama√√ (2)
1.3.2 Caliph√√ (2)
1.3.3 Brahman/Smartas√√ (2)
1.3.4 Anglican√√ (2)
1.3.5 Diviners/Izangoma/Amagqirha √√ (2)
1.4
1.4.1
- It is a belief in many supreme beings.√
- It could also mean many manifestations of one God. √ (2)
1.4.2
- A substitute for religion√
- It is a system or a set of beliefs.√
- Values and opinions that determine the way a person or a group behaves and thinks. √
- It is the science of ideas. √ (2)
1.4.3
- They believe that a being is born into a next life over and over again.√
- The rebirth of the soul or spirit in a new body. √ (2)
1.4.4
- It is the acceptance of things as they are.√
- A person in Nirvana can make decisions and choices not out of emotional turmoil and suffering, but from a position of knowing the consequences of his or her actions. √ (2)
1.4.5
- A small religious group. √
- It is regarded by mainstream religion as deviating from the original teachings. √ (2)
1.5
1.5.1
- False, √ yoga is a spiritual discipline including breath control, simple meditation, and specific body postures.√
- Baptism is a sacrament in which a convert is made a full member of a particular Christian community. (2)
1.5.2 False,√ in Taoism, spontaneity and flexibility are the characteristics of the path that the universe travels.√ (2)
1.5.3 False,√ the Ten Commandments were revealed to Moses. (2)
1.5.4 True.√√ (2)
1.5.5 False,√ it is a sacred text for the Latter Day saints Movement.√ False, the sacred text of the Baha'i Faith is called Kitab-i-Aqdas (2)
1.6
1.6.1
- It is a set of religious beliefs or principles. √
- It is another word for 'teaching'. √
- It provides the central frame of reference for a religion. √ (2)
1.6.2
- It comes from the Greek word 'mythos' which means 'word' or 'fable'.√
- It is those religious stories in which deep truths about life are revealed. √
- They are sacred stories that explain why the world is as it is and the nature of human experience. √ (2)
TOTAL SECTION A 50
SECTION B
QUESTION 2
2.1
2.1.1
- Difference is the opposite of similarity.
- It can be used to differentiate between specific religions.
- Example: Christians believe that the Messiah has already come to the world whereas those who believe in the Jewish faith are still waiting for the Messiah. (4)
2.1.2
- Teachings come from the verb 'to teach', i.e. to impart knowledge.
- In the context of religion, it refers to imparting knowledge, values, attitudes and norms.
- Teachings communicate the deeper meanings of the world and how life operates.
- Teachings also mean to give systematic information about a subject.
- In some religions, teachings are highly significant whilst in others they are less important.
- Example: Buddhism is far less inclined to stress systematic teachings than most Christian groups. (4)
2.1.3
- This is the way of Higher Truths.
- Dharma implies the universal laws of nature that uphold the cosmos.
- It is also the way of the doctrines in the Buddhist religion.
- Dharma carries the teachings of Buddha.
- Dharma integrates within its meaning certain concepts.
- For example: Justice, virtue, morality, righteousness, law and duty. (4)
2.1.4
- Syncretism is a state in which two different belief systems are combined to form one.
- This can be experienced in the African Indigenous Churches in which Christianity is combined with the African Traditional Religion.
- Another example is Sikhism which combines Hinduism and Islam. (4)
2.1.5
- This is where an adherent believes that only their view of divinity is true.
- In this case the believer also believes that other religious views different from his or hers are false.
- For example in Christianity: Jesus Christ is believed to be the only ONE who is the way and the truth and that He is God himself. (4)
2.2
2.2.1 Christianity
- Christians believe that God sent His Son, Jesus Christ to save the world from sin, so that all humanity can live forever.
- Christians believe that Jesus is God's Son.
- Christians believe and teach that Jesus was resurrected from the dead after He was crucified.
- Jesus is the only true Messiah that God sent to earth and that one day He will return. (6)
2.2.2 Taoism
- According to Taoism, divinity refers to any being or object that is divine or god-like.
- The Tao that can be told of is the eternal Tao.
- According to Taoism, all things come from being, and being comes from non-being.
- Everything consists of two things: Yin and Yang. (6)
2.2.3 African Traditional Religion
- In the African Traditional Religion, there is no special day of worship.
- The emphasis is on practice.
- Individualism is discouraged; it is regarded as inhuman (communal way of life).
- The moral order in African Traditional religion is characterised by the concept of 'ubuntu.'
- They believe in ancestors. (6)
2.3
- Uniqueness in a religion helps the members to explain why they have chosen that religion.
- Uniqueness helps the members to strengthen their faith.
- It also helps members to identify who belongs and who does not belong.
- Uniqueness of various religions assists in enriching the wider society with values and morality.
- Uniqueness also provides believers with reasons for why their religion is 'best'.
- It provides the features that distinguish each religion from the other.
- Uniqueness strengthens the unity of the members in a particular religion. (12) [50]
QUESTION 3
3.1
3.1.1
- It teaches that South Africans can be a united people, despite their apartheid past.
- Religion should not be a divisive force.
- This is evidenced by the fact that numerous religions were accommodated at the funeral.
- We should never be divided along racial lines: we should see one another as human beings.
- This is shown by the fact that Kathrada was married to a White woman, in a time when inter-racial marriages were illegal.
- A person who made great sacrifices for humanity will always be acknowledged and respected.
- This is clear as many political organisations, race groups and religions paid respect to Kathrada.
- No race group should be dominated by another. This will bring about racial harmony.
NOTE: Other relevant responses must be accepted. (12)
3.1.2
- There is utmost respect and tolerance for religious differences.
- This is demonstrated by the fact that an Anglican Archbishop prayed at a Muslim funeral.
- Also, many religions were represented.
- In addition, racial differences are overcome
- Racial stereotypes are challenged, as Kathrada's wife was white and an activist in the freedom movement.
- Freedom of speech is respected.
- Ahmed Kathrada's wish that the President of the country step down was read out at the funeral.
- South Africans remember and honour the sacrifices of one of South Africa's veterans in the liberation of our country.
- This is why the funeral was attended by people of all races and religions.
NOTE: Other relevant responses must be accepted. (12)
3.1.3
- There is much negativity about South Africa, in terms of its economic and political challenges.
- Despite this, Ahmed Kathrada's funeral illustrated that racial and religious differences can be overcome.
- As long as there is hope, people will strive for a better South Africa.
- Although the odds are stacked against us, there is hope that we shall overcome these challenges. (6)
3.1.4 Advantages
- Social media presents up-to-date information to the public.
- Religious organizations can use social media to promote themselves.
- Different religions can use media to announce their activities e.g. Easter celebrations in Christianity, Diwali celebrations in Hinduism.
- Individuals can also air their views on different aspects of life.
- Social media can assist in ensuring that messages that are intended for specific sections of the community reach the intended recipients.
- They can also use media to convey messages of hope to the whole nation. (6)
Disadvantages
- It can promote radical personal opinions that may impact negatively on significant religious issues.
- It can be an effective tool for religious propaganda.
- It may cause degeneration of moral values in society, as children can have easy access to undesirable material.
- People can become addicted to media and live self-centred lives. (6)
3.2
- Reporters often do not have the specialist knowledge to interpret religious issues.
- The media relies on generation of income. They therefore report selectively on issues that will sell newspapers.
- Editorial decisions are influenced by political interests.
- Advertisers also influence how religious issues are covered in the media.
NOTE: Other relevant points must be credited. (8) [50]
QUESTION 4
4.1
4.1.1
- Colonialism is a policy or practice where a wealthy or powerful nation maintains control over other countries/nations.
- According to the extract, colonialism refers to the taking of land by white people without the permission of the indigenous occupants.
- Under the pretext of religion, colonialists stole the land.
- Colonialists used religion to subjugate (control) the indigenous people.
- Colonialists used prayer and the Bible to take away the land from their owners. (4)
4.1.2 YES
- The majority of Africans in our country are Christians.
- This is the influence of Christian missionaries.
- However, they do not own the land, but they are like foreigners in their own country.
- The blacks, who are the majority in South Africa, are excluded from the economy of the country because they have no land.
- Most black South Africans live in informal settlements which have no infrastructure, because the ownership of the land is in question.
- The white monopoly capitalists are the owners of the land in our country. They used illegal methods to take land from indigenous blacks.
- Christianity was used as a tool to take the land that belonged to the Africans.
NO
- Missionaries had come to spread the Gospel of Christ.
- Missionaries introduced health services.
- They also introduced education and built schools.
- The white man brought technology for the benefit of all.
- They facilitated the development of indigenous languages and translated the Bible into different African languages.
- This shows that they were sincere in propagating the religion.
- The issue of land ownership is a complex one, with some land belonging to tribal authorities.
- Individual ownership of that land is not permissible.
- The government is still dealing with the land claim issue. (12)
4.1.3
- Interreligious dialogue refers to the communication between two or more religions.
- Intrareligious dialogue occurs between two or more branches of the same religion.
- Interreligious dialogue occurs on matters of common interest and particular issues that different religions find necessary to engage on.
- Intrareligious dialogue takes place when the branches of the same religion engage each other on matters of common interest and other issues that may be found necessary to be discussed.
- An example of intrareligious dialogue is the dialogue between the Catholic and Protestant branches of Christianity through the Lutheran World Council.
- An example of interreligious dialogue is the World Conference of Religions for Peace which was established in 1961. (8)
4.2 EXAMPLE 1: Name of the Organisation
Interfaith Action for Peace in Africa
Achievements:
- Bringing together religious communities, civil society, private sector and governments.
- Being inclusive of different religions e.g. African Traditional Religion, Christianity, Judaism, Islam, Hinduism, Buddhism and Baha'i Faith.
- It has been able to send its delegation to the areas of conflict.
- Its members have also been able to bring conflicting groups together in reaching understanding and co-operation among each other.
- The members of this organisation have been able to participate in the legislative election in Togo.
- They have been able to organise exchange visits between landmine victims and survivors from Ethiopia, South Sudan and Uganda.
- They were also participating in the World Social Forum held in Kenya (2007).
- They also sent women's delegation to Nordic countries.
- They were also successful in forming IFAPA Women Network.
- This organisation was also able to organise the Nakanyonyi Youth consultation forum.
EXAMPLE 2: Name of the Organisation
African Women of Faith Network
Achievements:
- They have been able to solve some problems in Africa, such as poverty and illness.
- They have also made an important contribution towards solving conflict in Africa.
- They have made a contribution towards change and development in Africa.
- They have also been successful in dealing with challenges of poverty and lack of education faced by women in African communities.
- They have worked to uplift women by teaching them skills and providing financial support.
- They have also worked hard towards educating women about their human rights.
- They have also made a significant contribution towards the fight against HIV and AIDS pandemic.
- They have managed to make a considerable contribution towards bringing about peace and justice in Africa as a whole.
NOTE: Other Africa-based organisations must be credited. (16)
4.3 Interfaith Action for Peace in Africa
- This is a pan-African non-profit organisation.
- It was founded in 2002.
- this organisation was established to unite religious communities across Africa.
- This organisation was also established to promote co-operation among religions.
- It was also initiated to combine the efforts of different religions to work for peace in the African continent.
African Women of Faith Network
- This organisation has strong connection with the African Council of Religious Leaders (ACRL).
- This organisation is made up of women from different religious organisations.
- It was formed so that women could make the contribution towards change and development.
- This organisation was formed to in order to solve socio-economic problems in Africa.
- The African Women of Faith Network was established so that it included members from across the continent. (10) [50]
QUESTION 5
5.1
- The World Conference of Religions for Peace (WCRP) has its branches in many different countries of the world, which stand together against the use of religion to support violence and human sufferings.
- The European Council of Religions Leaders, affiliate of the WCRP strongly appealed to all religious leaders of all faiths to reject and do their best to stop the on-going acts of violence and terror, which are carried in the name of God.
- The WCRP and its affiliates responded strongly against the publication of cartoons considered by Muslims to be offensive.
- The Western Europe Interfaith Youth Organisation through the development of interfaith network have achieved their goal and played an active role in the progression towards world peace.
- There is a general acceptance among religious groups that there is more religious tolerance now than it used to be in the past due to WCRP.
NOTE: ANY relevant response must be credited. (8)
5.2
- In African Traditional Religion, the principle of 'Ubuntu' places the needs of the community above those of the individual. This ensures good morality, as a person may not cause harm to others.
- In Christianity, the Ten Commandments speak to harmful actions that are prohibited.
- This leads to good morality. e.g. 'love your neighbour as you love yourself.'
- Islam teaches as follows: 'And in their wealth and possession there was due share for the beggar and for one who is denied (goods).'
- This teaching encourages caring for the poor by means of compulsory charity.
- According to Buddhism, devotees are taught to refrain from telling lies, but to speak in a kind and purposeful way.
- According to Hinduism, one should 'speak words that are truthful, pleasant, beneficial, and not causing distress or anxiety, as well as the study and recitation of scriptures – this is austerity of speech.' (BG 17.15)
NOTE: Other relevant responses must be credited. (10)
5.3
- There was much more interfaith cooperation during the apartheid years.
- All religions were facing one common enemy which was apartheid.
- If an imam was killed in detention, Jews, Christians, Hindus and others joined in the protest, just as they would for their own.
- The South African branch of the World Conference of Religions for Peace (WCRP) led by Rev. Frank Chikane and Archbishop Desmond Tutu, played a significant role.
- Different religions held joint prayer meetings to plead for the divine intervention.
- Religious properties e.g. church buildings were used for political gatherings.
- Religious communities led and participated in the public marches against apartheid laws.
- Anti-apartheid groups included the South African Council of Churches which was formed in 1968.
- The call of Islam was formed in 1984.
- Jews for justice was formed in 1985. (12)
5.4
5.4.1
- The concept of religious freedom implies that everyone everywhere has the freedom of choice to believe what they wish to about God.
- It also means that people cannot be forced to convert to another religion.
- In South Africa, people enjoy religious freedom, and the Constitution prohibits unfair discrimination. (4)
5.4.2
- The concept 'human rights' is believed to have existed for centuries.
- Human rights refer to the inherent dignity of human beings
- Human rights are important since they protect human beings from exploitation.
- Human rights are important since they acknowledge the equality of every human being.
- Human rights provide all human beings with specific rights and responsibilities. (4)
5.4.3
- n South Africa all religions use the opportunity provided by government to participate in matters of State.
- An example of this is the NRLF (National Religious Leaders' Forum), which advises on social challenges and religious matters.
- Catholics and Muslims prayed together in Durban in 2016 to demonstrate religious tolerance and religious freedom.
- Pope John-Paul II also visited the Palestinian and Jewish communities preaching religious freedom and tolerance.
- The humanitarian organization Gift of the Givers is an inter religious organization that does charitable work across all religious groups.
- In conflict areas like Sudan, religious organizations are involved in finding solution against government who abuse humans' rights.
- Inter-Faith Action for Peace in Africa (IFAPA) always sent its delegates as observers in most African general elections.
- Every religion encourages its adherents to follow teachings that promote human rights (12) [50]
TOTAL SECTION B: 100
GRAND TOTAL: 150