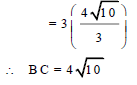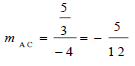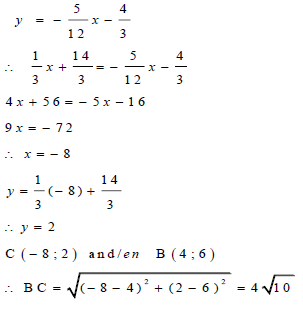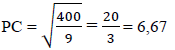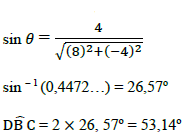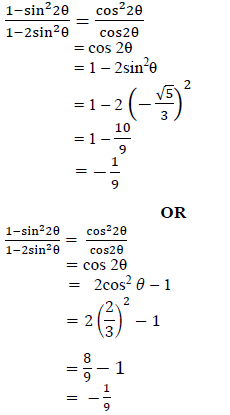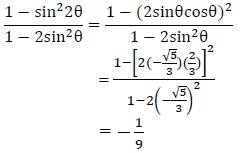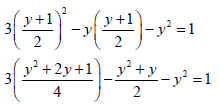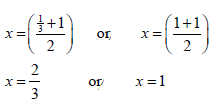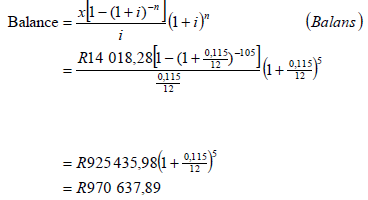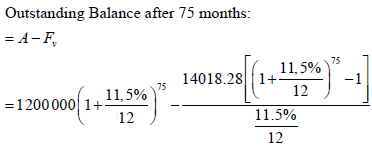Adele
Physical Sciences P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
MEMORANDUM
QUESTION 1:
MULTIPLE-CHOICE QUESTIONS
1.1 C ?? (2)
1.2 A ?? (2)
1.3 B ?? (2)
1.4 C ?? (2)
1.5 D ?? (2)
1.6 A ?? (2)
1.7 D ?? (2)
1.8 B ?? (2)
1.9 A ?? (2)
1.10 D ?? (2) [20]
QUESTION 2
2.1 A body will remain at rest or motion with constant velocity unless a non-zero resultant/net force acts on it. ??
OR
An object will continue in a state of rest or uniform velocity, unless it is acted upon by an unbalanced force. ??(2)
NOTE:
- If any of the underlined key words in the correct context is omitted deduct 1 mark.
2.2 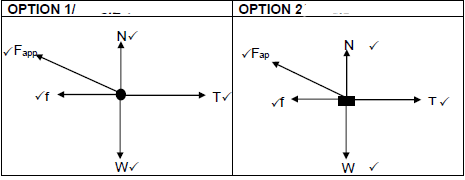
(5)
- Accept if learners draw the components of the applied force.
- Mark awarded for arrow and label.
- Do not penalise for length of arrows since drawing is not drawn to scale.
- Any other additional force(s) 4/5
- If force(s) do not make contact with body. Max. 4/5
2.3
(5)
2.4 Positive marking from 2.3
fk =μkN
32 = (0,12) N? Any one ?
N = 266,67 N
OR
N = mg – Fsinθ
266,67 = m x 9,8 – 88 sin13,41º ?
m = 29,29 kg? (4)
2.5 Remains the same ? (1) [17]
QUESTION 3
3.1
3.1.1
| OPTION 1 UPWARD POSITIVE | OPTION 2 UPWARD NEGATIVE |
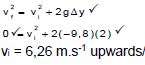 |  |
(4)
3.1.2
| OPTION 1 UPWARD POSITIVE | OPTION 2 UPWARD NEGATIVE |
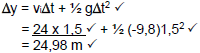 | 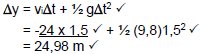 |
| OPTION 3 UPWARD POSITIVE | OPTION 4 UPWARD NEGATIVE |
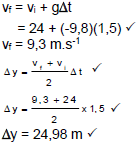 | 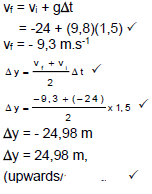 |
(4)
3.2 Positive marking from 3.1.1
| OPTION 1 UPWARD POSITIVE | OPTION 2 UPWARD NEGATIVE |
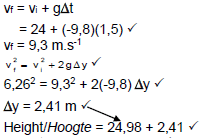 | 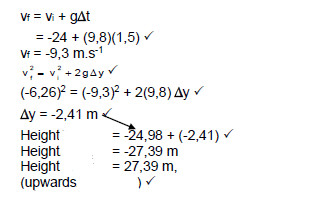 |
(6) [14]
QUESTION 4
4.1 In an isolated system total linear momentum is conserved. ?? (2)
NOTE:
- If any of the underlined key words in the correct context is omitted deduct 1 mark.
4.2 EAST IS POSITIVE
- ∑pi = ∑pf
mAviA + mBviB = mAvfA + mBvfB
mAviA + mBviB = (mA + mB)vf
52,5 x viA + 42 x -4 ? = 0 ?
viA = 3,2 m.s-1, right/regs ? (4)
4.3 670 N west/wes ? (No mark if only magnitude is given) (1)
4.4
- Fnet ∆t = ∆p
Fnet ∆t = mvf - mvi
670 x 0,5 ? = 42 (vf – 0) ?
vf = 7,98 m.s-1 ? (4) [11]
QUESTION 5
5.1 In an isolated system the total mechanical energy remains constant. ?? (2)
NOTE:
- If any of the underlined key words in the correct context is omitted deduct 1 mark.
5.2
- WFg = - ΔEp
WFg = - mg (h2 – h1)
WFg = -1,5 x 9,8 (0 – 3) ?
WFg = 44,1 J ? (3)
5.3 A force is non-conservative if the work it does on an object which is moving between two points depends on the path taken. ?? (2)
NOTE:
- If any of the underlined key words in the correct context is omitted deduct 1 mark.
5.4 Positive marking from 5.2
| OPTION 1 | OPTION 2 |
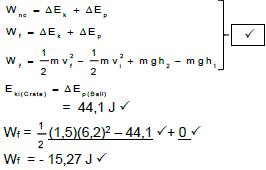 | 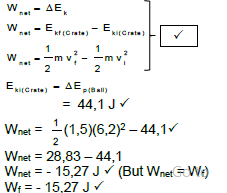 |
| OPTION 3 | |
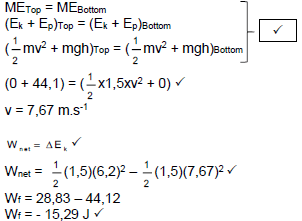 | |
(5) [12]
QUESTION 6
6.1 The change in frequency (or pitch), of the sound detected by a listener because the sound source and the listener have different velocities relative to the medium of sound propagation. ??
OR
An (apparent) change in observed/detected frequency (pitch), as a result of the relative motion between a source and an observer. ?? (2)
NOTE:
- If any of the underlined key words in the correct context is omitted deduct 1 mark.
6.2 871 Hz ? (1)
6.3 As the learner stands next to the sound source, the detector registers the frequency of the source because there is no relative motion. ? As the learner moves away from the source the waves become stretched out, ? the wavelength become longer and the frequency become lower. ? (3)
6.4
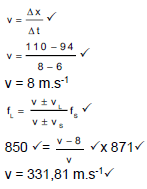 (7)
(7)
6.5
- Used to measure the direction and speed of blood flow in arteries and veins. ? ?
- Used to monitor the heartbeat of a newly formed foetus. ? (2) [15]
QUESTION 7
7.1 25º ? (1)
7.2 The magnitude of the electrostatic force exerted by one point charge (Q1) on another point charge (Q2) is directly proportional to the product of the (magnitudes) of the charges and inversely proportional to the square of the distance (r) between them. ?? (2)
NOTE:
- If any of the underlined key words in the correct context is omitted deduct 1 mark.
7.3
- T sin θ = FE
480 sin 25° = FE ?
FE = 202,8567656 N
FE = kQ1Q2?
r2
202,8567656 ?= 9 x 109 x Q2 ?
0 , 022
Q = 3,00 x 10-6 C ? (5)
7.4.1 Positive marking from 7.3.
| OPTION 1 | OPTION 2 |
 | 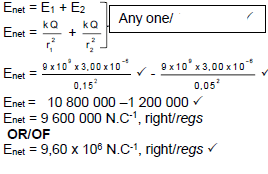 |
(5)
7.4.2 Positive marking from 7.3.
| OPTION 1 | OPTION 2 |
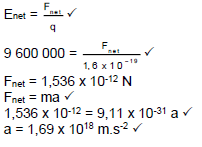 | 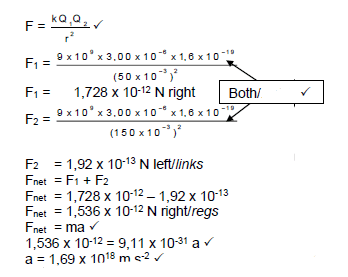 |
[18]
QUESTION 8
8.1
| OPTION 1 | OPTION 2 |
1 = 1 + 1 | RP = R1R2 R1 + R2 RP = 6 × 8 6 + 8 RP = 3,43 Ω ? |
(3)
8.2
8.2.1
- Cost= E(kWh) x price
6,75 = E(kWh) x 1,50 ?
E(kWh) = 4,5 kWh
P = W ?
Δ t
P = 4 , 5 ?
5 x 5
P = 0,18 kW
P = 180 W ? (4)
8.2.2 Positive marking from 8.2.1
P = VI ?
180 = (60)I ?
I = 3 A ? (3)
8.3
8.3.1 Positive marking from 8.1 and 8.2.2
R = V ?
I
1 = V ?
3
Vr = 3 V
Vp = 10,29 V
Emf = Vload + Vr
Emf = 60 + 10,29 + 3 ?
Emf= 73,29 V ? (5)
8.3.2 Positive marking from 8.1, 8.2.1 & 8.2.2
| OPTION 1 | OPTION 2 |
| | 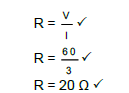 |
| OPTION 3 | OPTION 4 |
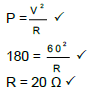 | 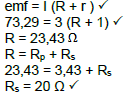 |
QUESTION 9
9.1 Mechanical ? to electrical ?
9.2 To reverse the direction of the current each half cycle. ?
OR
Allow for constant direction of rotation of the coil. ?
9.3
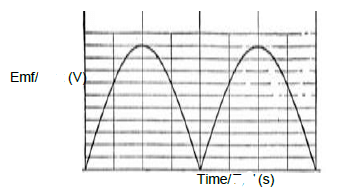
- D.C.graph
- Two peaks only (one cycle)
9.4
- Increase the strength of the magnetic field
- Increase the number of turns on the coil
- Rotate the coil faster
Any one ?
QUESTION 10
10.1 The DC potential difference/voltage that dissipate the same amount of energy as an AC source. ?? (2)
NOTE:
If any of the underlined key words in the correct context is omitted deduct 1 mark.
10.2
| OPTION 1 | OPTION 2 |
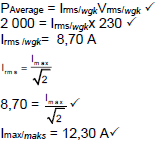 | 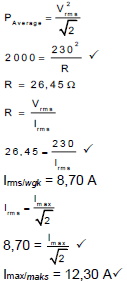 |
QUESTION 11
11.1 The minimum frequency required to emit electrons from a metal surface. ?? (2)
NOTE:
If any of the underlined key words in the correct context is omitted deduct 1 mark.
11.2
- Wo = hfo ?
Wo = (6,63 x 10-34)(1,50 x 1014) ?
Wo = 9,95 x 10-20 J ? (3)
11.3 Positive marking from 11.2
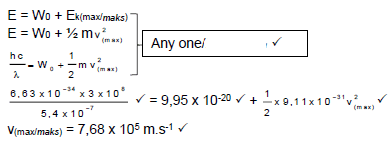
11.4
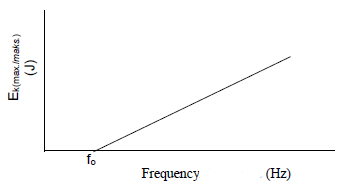
Correct shape | ? |
Both axes labeled | ? |
Threshold frequency, fo | ? |
TOTAL: 150
Physical Sciences P2 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
- Write your full NAME and SURNAME in the appropriate spaces on the ANSWER BOOK.
- This question paper consists of TEN questions. Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page in the ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Leave ONE line between two sub-questions, for example between QUESTION 2.1 and QUESTION 2.2.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, et cetera where required.
- You are advised to use the attached DATA SHEETS.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1–1.10) in the ANSWER BOOK, for example 1.11 D.
1.1 The reaction represented by the balanced equation below occurs in the second step of the contact process.
2SO2(g) + O2(g) ⇌ 2SO3(g)
The catalyst used in the reaction above, is …
- nickel.
- platinum.
- iron (II) oxide.
- vanadium pentoxide. (2)
1.2 Which ONE of the following homologous series is saturated hydrocarbons?
- Esters
- Alkanes
- Alkenes
- Alkynes (2)
1.3 Which ONE of the following pairs of compounds are members of the same homologous series?
- C3H6 and C4H10
- CH4O and C2H4O2
- C2H4O2 and C3H6O2
- C3H6 and C4H6 (2)
1.4 In the flow diagram below, butane, C4H10, reacts to produce compound B in reaction 1. Compound B undergoes addition polymerisation to produce polyethene.
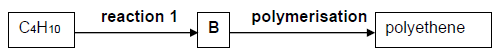
The name of the reaction represented by reaction 1, is …
- cracking.
- hydration.
- dehydration.
- dehydrohalogenation. (2)
1.5 The yield in a certain reversible reaction at equilibrium at temperature T and pressure P is 40%.
A catalyst is added to the reaction mixture at the start of the reaction and the reaction reaches equilibrium at the same temperature T and pressure P.
What effect will the addition of a catalyst have on the yield and rate of reaction?
| yield | reaction rate | |
| A | remains 40% | higher |
| B | remains 40% | Remains the same |
| C | higher than 40% | higher |
| D | higher than 40% | remains the same |
1.6 The graphs given below show how the vapour pressure of a secondary alcohol and a tertiary alcohol of equal molecular mass change with temperature.
Atmospheric pressure = 760 mmHg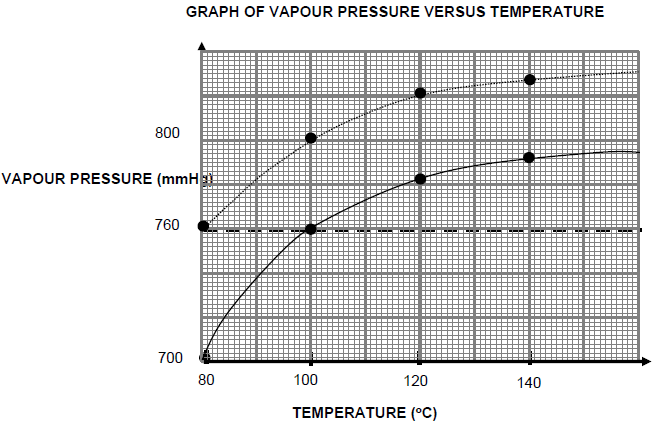
Which ONE of the following is the boiling point (in °C) of the secondary alcohol?
- 80
- 100
- 120
- 140 (2)
1.7 The following acid-base reactions occur spontaneously at the same temperature. All the solutions have the same concentration.
HPO42- (aq) + CO32- (aq) → PO43- (aq) + HCO3-(aq)
HPO42- (aq) + HSO4- (aq) → H2PO4-(aq) + SO42-(aq)
The dissociation constants (Kb values) are as follows:
K1 for HPO4-
K2 for CO32-
K3 for HSO4-
Which ONE of the following CORRECTLY shows the order of increasing Kb values?
- K1, K2, K3
- K3, K2, K1
- K2, K1, K3
- K3, K1, K2 (2)
1.8 Which ONE of the salts below produce an acidic solution when dissolved in water?
- Na2CO3
- NaCℓ
- NH4Cℓ
- KNO3 (2)
1.9 Which ONE of the following is the strongest reducing agent?
- Ni
- Cr2+
- Sn2+
- Ag (2)
1.10 An iron nail is electroplated with silver.
The half reaction taking place at the iron nail is given by:
- Fe2+ + 2e- → Fe
- Fe → Fe2+ + 2e-
- Ag → Ag+ + e-
- Ag+ + e- → Ag (2)
[20]
QUESTION 2 (Start on a new page.)
Three organic compounds (A, B and C) with different functional groups are given below.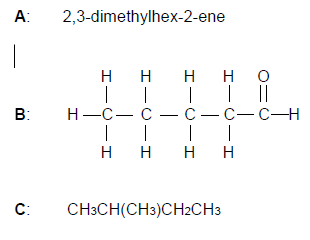
2.1 Write down TWO special properties of carbon which make it possible for carbon to form such a variety of organic compounds. (2)
2.2 Define the term functional group. (2)
2.3 Write down the:
2.3.1 Structural formula of compound A (2)
2.3.2 IUPAC name of compound B (2)
2.4 Compound C, pentane and a compound X are compounds that have the same molecular formula but different structural formulae.
Write down the:
2.4.1 Term used for the underlined phrase. (1)
2.4.2 Structural formula and IUPAC name of compound X (4)
[13]
QUESTION 3 (Start on a new page.)
The graph of the boiling point versus the number of carbon atoms for the first five STRAIGHT CHAIN alcohols and aldehydes is shown below.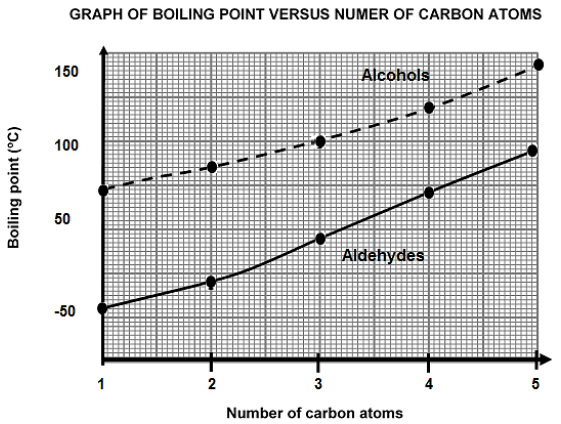
3.1 Define the term boiling point. (2)
3.2 Write down the IUPAC name of the alcohol with a boiling point of 100 °C. (2)
3.3 Explain fully why the curve for the alcohols is higher than that of the aldehydes. (5) The boiling points of carboxylic acids are generally HIGHER than those of their corresponding alcohols.
3.4 Explain the difference between the boiling points referring to the types of intermolecular forces present in each of these compounds. (3)
[12]
QUESTION 4 (Start on a new page.)
4.1 Consider the TWO reactions of haloalkanes with sodium hydroxide (NaOH) shown below.
- : CH3CH2CH2CH2Br

- : CH3CH2CHBrCH3

4.1.1 Which reaction (I or II) is classified as elimination reaction? (1) Write down:
4.1.2 The IUPAC name of the ORGANIC product formed in reaction I. (2)
4.1.3 A balanced equation for reaction II using structural formulae for the organic reagents. (5)
4.2 Consider the TWO organic compounds (A and B) shown below.
- : C4H8
- : C4H10
4.2.1 Which organic compound (A or B), will undergo addition reactions? Give a reason for the answer. (2)
4.2.2 Write down the NAME of an inorganic substance that reacts with compound A to produce compound B. (1)
4.3 Butanol reacts with organic compound Y in the presence of a concentrated inorganic acid to produce an ester. The equation shown below represents the reaction.
CH3CH2CH2CH2OH + Y → CH3CH2CH2CH2OOCCH2CH3 + H2O
Write down the:
4.3.1 Function of the concentrated inorganic acid in the reaction. (1)
4.3.2 Condensed structural formula of compound Y (2)
4.3.3 IUPAC name of the ester produced (2)
4.3.4 ONE piece of evidence that will indicate that an ester has been produced (1)
[17]
QUESTION 5 (Start on a new page.)
A group of learners use the reaction between magnesium and hydrochloric acid to measure the average rate at which hydrogen gas is produced. They add 10 cm3 of a 1 mol·dm-3 of HCℓ to 0,048 g magnesium powder in an Erlenmeyer flask at 20ºC.
The balanced equation for the reaction is: Mg(s) + 2HCℓ(aq) → MgCℓ2(aq) + H2(g)
The learners’ experimental results were plotted to produce graph A.
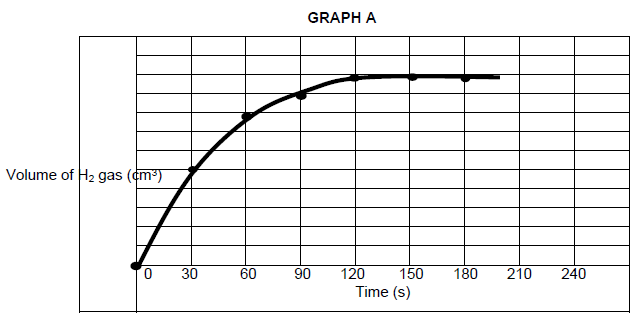
5.1 Define reaction rate. (2)
5.2 Calculate the volume of hydrogen gas produced in the first minute if the average rate of production of hydrogen gas is 0,67 cm3·s-1. (3)
5.3 How long (in seconds) does the reaction take to run to completion? Give a reason for the answer by referring to the gradient of the graph. (2)
5.4 Calculate the mass of the reactant left in the flask when the reaction is complete. (7)
5.5 When the concentration of hydrochloric acid is increased the learners observe that the rate of reaction increases. Use the collision theory to explain this observation. (2)
5.6 In another experiment the magnesium powder is replaced with an equal amount of zinc powder. Redraw the graph provided above in your ANSWER BOOK and sketch on the same axis the graph that would be obtained when zinc powder is used. (2)
[18]
QUESTION 6 (Start on a new page.)
The decomposition reaction of hydrogen iodide, HI represented by the balanced equation below reaches equilibrium in a closed container at 25ºC.
2HI(g) ⇌ H2(g) + I2(g) ∆H>0
6.1 How does the rate of the forward reaction compare to the rate of the reverse reaction at the following stages?
Choose from HIGHER THAN, LOWER THAN or EQUAL TO
6.1.1 At equilibrium (1)
6.1.2 Before the reaction reaches equilibrium for the first time? (1)
6.2 What effect will an increase in pressure, by decreasing the volume at constant temperature have, on the concentration of H2 at equilibrium?
Choose from INCREASES, DECREASES or REMAINS THE SAME (2)
6.3 The reaction is started by pumping a certain amount of hydrogen iodide, HI into an empty flask which is then sealed.
The equilibrium concentration of two of the substances at 25ºC was found to be:
[I2] = 0,026 mol·dm-3
[HI] = 0,72 mol·dm-3
When temperature of the equilibrium mixture is increased, the equilibrium position shifts and a new equilibrium is established at 448ºC. At the new equilibrium the concentration of hydrogen, H2 is found to be 0,084 mol·dm-3.
Calculate the equilibrium constant for the reaction at 448ºC. (7)
6.4 What effect will the increase in temperature, from 25ºC to 448ºC, have on the rate of the reverse reaction? Choose from INCREASES, DECREASES or REMAINS THE SAME. (1)
[12]
QUESTION 7 (Start on a new page.)
7.1 Acid-base indicators are generally represented by the formula, HIn. The reaction of HIn with water can be represented by the following equation.
HIn + H2O ⇌ H3O+ + In-
colourless pink
Acid-base indicators are considered to be weak acids.
7.1.1 Define the term weak acid. (2)
7.1.2 Is H2O acting as an ACID or a BASE in the reaction? (1)
7.1.3 Write down the formula of the conjugate base of HIn. (1)
7.2 Vinegar is a solution of ethanoic acid, CH3COOH. A certain manufacturer of vinegar claims that the vinegar she sells contains 5,80 grams of ethanoic acid per 100 mℓ vinegar solution.
A group of learners used the apparatus shown below to test the claim by the manufacturer.
They titrated a dilute sample of vinegar against a standard sodium hydroxide solution (NaOH) of concentration 0,1 mol·dm-3 using HIn as the acid-base indicator.
The balanced equation for the reaction is given below:
NaOH(aq) + CH3COOH(aq) → CH3COONa(aq) + H2O(ℓ)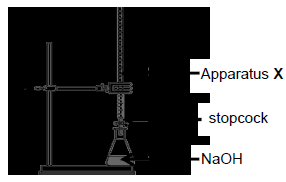
7.2.1 Write down the name of apparatus X. (1)
7.2.2 Use the equation in QUESTION 7.1 to determine the colour change that will take place at the end-point.
Choose from PINK TO COLOURLESS or COLOURLESS TO PINK.
Use Le Chatelier’s principle to explain the answer. (4)
7.2.3 Calculate the pH of the sodium hydroxide (NaOH) solution before titration. (4)
7.2.4 The dilute solution of vinegar used in the titration was obtained by adding 10 cm3 of vinegar to water and filling up with water to a volume of 100 cm3 of dilute vinegar solution.
During the titration 18 cm3 of sodium hydroxide solution of concentration 0,1 mol·dm-3 neutralises exactly 20 cm3 of the diluted vinegar.
Determine by calculation whether the manufacturer’s claim is TRUE or NOT. (8)
[21]
QUESTION 8 (Start on a new page.)
The diagram given below shows a galvanic cell set up under standard conditions.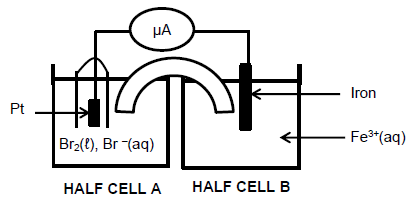
8.1 Write down TWO functions of the salt bridge. (2)
8.2 Which half-cell, A or B, contains the cathode? (1)
8.3 Write down the balanced equation for the overall (net) cell reaction. (3)
8.4 Calculate the initial EMF of this cell. (4)
8.5 The Br2|Br- half cell is now replaced with the I2|I- half-cell at standard conditions. Will the initial ammeter reading be HIGHER or LOWER when the I2|I- is used? Explain the answer by referring to the relative strengths of the oxidising agents involved. (3)
[13]
QUESTION 9 (Start on a new page.)
The diagram below show the apparatus used to demonstrate the electrolysis of concentrated copper(II) chloride (CuCℓ2) solution.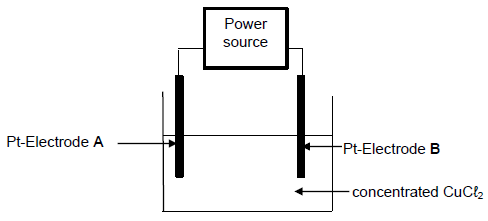
9.1 Write down the energy conversion which occurs in the cell above. (2)
9.2 Explain why an AC-power source is not suitable for this cell. (2)
A reddish-brown layer is observed on electrode A after the cell has been functioning for a while.
9.3 Write down the half reaction that occurs at electrode A.
The copper(II)chloride (CuCℓ2) solution is now replaced with a concentrated solution of sodium chloride (NaCℓ).
It is now observed that a gas is formed at electrode A. (2)
9.4 Write down the NAME of the gas that is formed at electrode A. (1)
9.5 Refer to the relative strengths of oxidising agents involved to explain why sodium (Na) metal does not form in this cell. (3)
[10]
QUESTION 10 (Start on a new page.)
The flow diagram below shows the industrial preparation of fertiliser Q.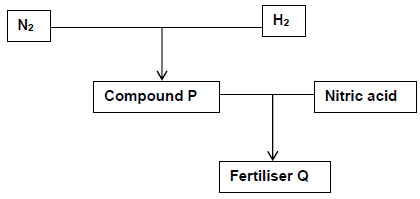
10.1 Write down:
10.1.1 The name of the process used to obtain nitrogen gas (N2) (1)
10.1.2 The name of compound P (2)
10.1.3 A balanced chemical equation for the production of fertiliser Q (3)
10.1.4 The name of the primary nutrient present in fertiliser Q (1)
10.2 Consider the three fertiliser bags shown below.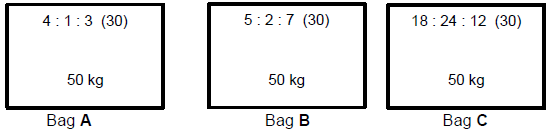
10.2.1 Which bag of fertiliser (A, B or C) is the most suitable for garden lawns?
Give a reason for the answer. (3)
10.2.2 Calculate mass of nitrogen in fertiliser bag C. (3)
10.3 Write down ONE negative impact of the overuse of fertilisers. (1)
[14]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES GRADE 12
PAPER 2 (CHEMISTRY)
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Standard pressure | pθ | 1,013 × 105 Pa |
Molar gas volume at STP | Vm | 22,4 dm3∙mol-1 |
Standard temperature | Tθ | 273 K |
Charge on electron | e | -1,6 × 10-19 C |
Avogadro’s constant | NA | 6,02 × 1023 mol-1 |
TABLE 2: FORMULAE
TABLE 3: THE PERIODIC TABLE OF ELEMENTS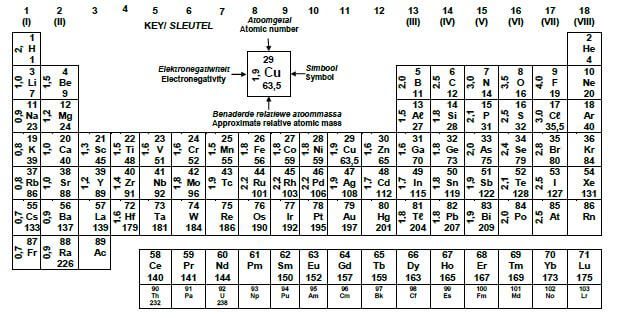
Physical Sciences P1 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
- Write your full NAME and SURNAME in the appropriate space on the ANSWER BOOK.
- This question paper consists of ELEVEN questions. Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page.
- Number the answers correctly according to the numbering system used in this question paper.
- Leave ONE line between two sub-questions, e.g. between QUESTION 2.1 and QUESTION 2.2.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your final numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, et cetera where required.
- You are advised to use the attached DATA SHEETS.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Four possible options are provided as answers to the following questions. Choose the answer and write only the letter (A–D) next to the question number (1.1–1.10) in the ANSWER BOOK, for example 1.11 D.
1.1 An object of mass m remains at rest when a force of magnitude F acts on it, as shown in the diagram below.
Which ONE of the following forces will increase if the force F acting on the object increases and the object still remains at rest?
- Normal force
- Gravitational force
- Static frictional force
- Kinetic frictional force (2)
1.2 A ball of mass m is thrown vertically upwards at a certain velocity.
Which ONE of the following physical quantities is not equal to zero when the ball reaches its maximum height?
- Net force
- Momentum
- Velocity
- Kinetic energy (2)
1.3 The graph below represents the net force acting on an object over a period of time.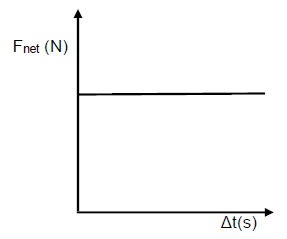
The area under the graph represents the object’s …
- momentum.
- impulse.
- rate of change of momentum.
- acceleration. (2)
1.4 Consider the following scenarios.
- A rocket accelerates through space.
- A brick falls freely from the top of a building to the ground.
- A learner moves around in the classroom carrying his school bag.
- A girl moves a wheelbarrow by pushing it in a straight line.
In which ONE of the scenarios above is work NOT being done on the object?- I
- II
- III
- IV (2)
1.5 A ball is thrown vertically upwards at a certain velocity.
Which ONE of the following is TRUE regarding mechanical energy and kinetic energy of the ball during its motion? Ignore air resistance.
MECHANICAL ENERGY | KINETIC ENERGY | |
A | Remains the same | Remains the same |
B | Increases | Decreases |
C | Decreases | Increases |
D | Remains the same | Decreases |
(2)
1.6 An observer stands at a distance x from a stationary ambulance which is sounding its siren at a certain frequency at an accident scene.
How does the pitch of the sound as heard by the observer compare with that which the siren produces?
- Equal to
- Greater than
- Less than
- Equal to zero (2)
1.7 Three identical point charges are arranged as shown in the diagram below, in a vacuum.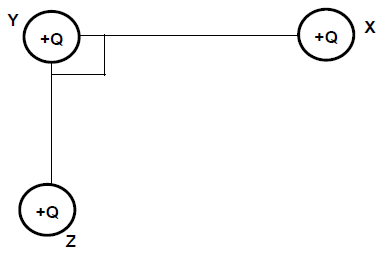
Which ONE of the following vector diagrams, NOT DRAWN TO SCALE, represents the electrostatic forces acting on sphere Y as well as the net electrostatic force acting on sphere Y?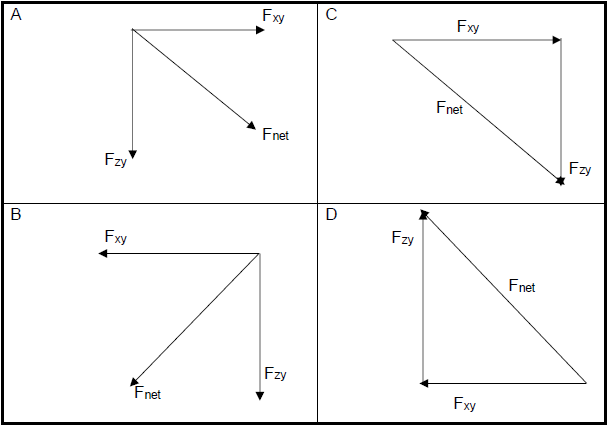 (2)
(2)
1.8 In the circuit diagram below the battery has an emf (ε) and internal resistance r. The ammeter and voltmeter both register readings. The resistance of the connecting wires can be ignored.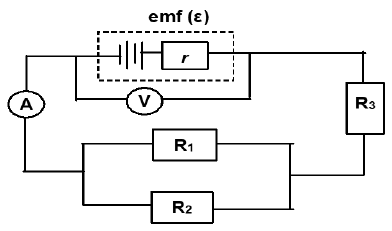
How will the reading on ammeter A and voltmeter V change if resistor R3 is removed from the circuit?
AMMETER READING | VOLTMETER READING | |
A | Decrease | Increase |
B | Increase | Decrease |
C | Increase | Remain the sane |
D | Remain the same | Decrease |
(2)
1.9 A coil is rotating in a uniform magnetic field and emf is induced in the coil.
Which ONE of the following is TRUE about the induced emf and position of the coil relative to the magnetic field?
Induced emf (V) | Position of coil relative to the magnetic field | |
A | Maximum | 0º |
B | Zero | 45º |
C | Maximum | 90º |
D | Zero | 60º |
(2)
1.10 Light from a 40 W blue light source is incident on a cathode of a photo-cell which is connected to an ammeter in a circuit as shown below. The ammeter does NOT show any reading.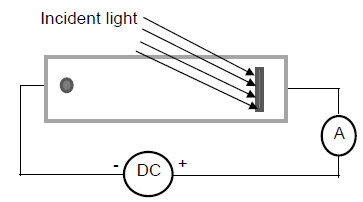
Which ONE of the light sources below is likely to cause the ammeter to show a reading?
- A 60 W blue light source
- A 100 W green light source
- A 150 W red light source
- A 40 W ultraviolet light source (2)
[20]
QUESTION 2 (Start on a NEW page.)
A block of mass m kg is placed on a rough horizontal surface. The block of mass m kg is connected to a 12 kg block by means of a light inextensible string passing over a light frictionless pulley, as shown below. A force of 88 N is applied at an angle θ to the horizontal to keep the 12 kg mass moving downwards at a CONSTANT VELOCITY.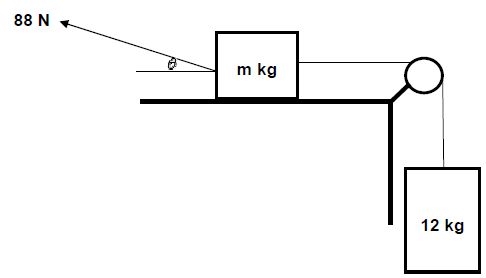
2.1 State Newton’s First Law of motion in words. (2)
2.2 Draw a labelled free-body diagram for the block of mass m. (5)
A constant frictional force of 32 N acts on block of mass m.
2.3 Calculate the magnitude of the angle θ that will keep the system moving at constant velocity. (5)
The coefficient of kinetic friction between block of mass m and the surface is 0,12.
2.4 Calculate the mass, m, of the block. (4)
2.5 How will the coefficient of kinetic friction be affected if the angle θ increases? Choose from: INCREASE, DECREASE or REMAIN THE SAME. (1)
[17]
QUESTION 3 (Start on a NEW page.)
An object is fired vertically upwards with a velocity of 24 m.s-1. After 1,5 s it enters the branches of a tree. It emerges from the highest point of the tree and continues vertically upwards to a maximum height of 2 m above the tree as shown in the diagram below. Ignore the effects of air resistance and any other forms of friction experienced by the object during its motion.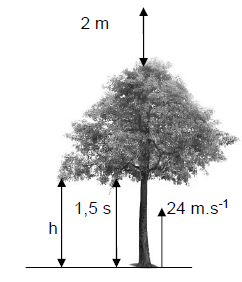
3.1 Calculate the:
3.1.1 Velocity with which the object emerges from the branches of the tree (4)
3.1.2 Height h above the ground at which the object enters the branches of the tree (4)
3.2 Calculate the height of the tree. (6)
[14]
QUESTION 4 (Start on a NEW page.)
Two ballet dancers, A of mass 52,5 kg moving with a velocity of v m.s-1 in a straight line to the east and B of mass 42 kg moving with a velocity of 4 m.s-1 to the west in a straight line, approach each other as shown in FIGURE 1.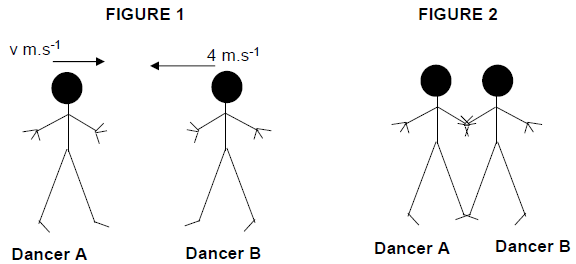
The two dancers grabbed each other and came to rest as shown in FIGURE 2. Ignore the effects of friction.
4.1 State the principle of conservation of linear momentum in words. (2)
4.2 Calculate the velocity of dancer A in FIGURE 1. (4)
After grabbing each other, dancer A pushed dancer B away with a net force of 670 N in 0,5 seconds and dancer A moves to the west, as shown in FIGURE 3.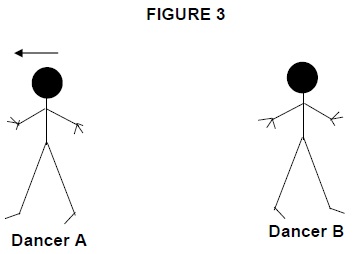
4.3 What is the force exerted by dancer B on dancer A? (1)
4.4 Calculate the magnitude of the velocity of dancer B in FIGURE 3. (4)
[11]
QUESTION 5 (Start on a NEW page.)
A steel ball of mass1,5 kg attached to an inextensible string hangs from a ceiling. The ball is held at a height of 3 m, at point A, above a horizontal table that has a 1,5 kg crate resting on it. The steel ball is released and it collides with the crate at point B. The collision is ELASTIC. The crate then moves to the left and attains a velocity of 6,2 m.s-1 after moving a certain distance, as shown in the diagram below.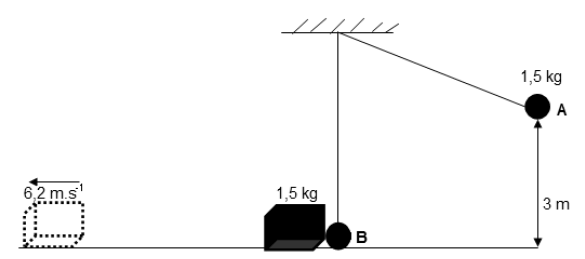
5.1 State the principle of conservation of mechanical energy in words. (2)
5.2 Calculate the work done by the gravitational force in moving the steel ball from point A to B. (3)
5.3 Define the term non-conservative force. (2)
5.4 Calculate the work done by friction in moving the crate. (5)
[12]
QUESTION 6 (Start on a NEW page.)
A group of learners conducted an experiment to determine the speed of sound on a particular day. At a particular point they placed a sound source emitting sound at a certain frequency. One learner walks away from the sound source at constant velocity with a detector which registers the frequency of the sound detected.
The graph below shows the detected frequencies versus time.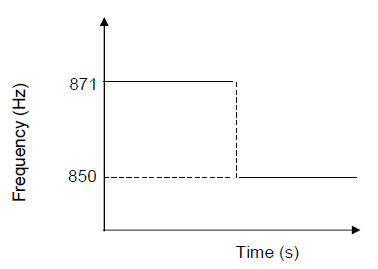
6.1 Define Doppler effect in words. (2)
6.2 Write down the frequency of the source. (1)
6.3 Explain in terms of wave motion why frequencies. the detector registers different (3)
Another learner records the time taken for the first learner to move from the point of the sound source to a particular point.
The graph below shows the position-time graph of the motion.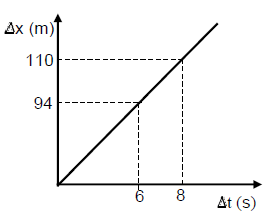
6.4 Calculate the velocity of sound on that particular day. (7)
6.5 Name TWO applications of Doppler effect in the medical field. (2) [15]
QUESTION 7 (Start on a NEW page.)
Two identical spheres, carrying equal charges, are held in a vertical position by means of an inextensible string as shown in FIGURE 1. When the spheres are released, they repel each other and come to rest with their centres 200 mm apart as shown in FIGURE 2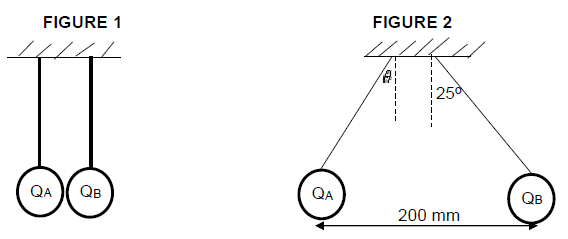
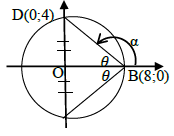
7.1 Write down the magnitude of angle, θ. (1)
7.2 State Coulomb’s law in words. (2) The tension in each string in FIGURE 2 is 480 N.
7.3 Calculate the charge on each sphere. (5)
7.4 An electron placed at point X experiences an acceleration as shown in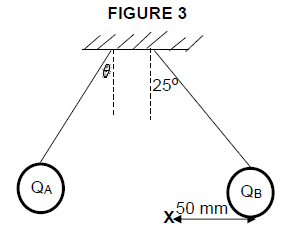
Calculate the:
7.4.1 Net electric field at point X, 50 mm from QB (5)
7.4.2 Acceleration of the electron (5)
[18]
QUESTION 8 (Start on a NEW page.)
A shaving machine is rated 60 V. The circuit diagram below represents a circuit used to provide a maximum voltage required by the shaving machine.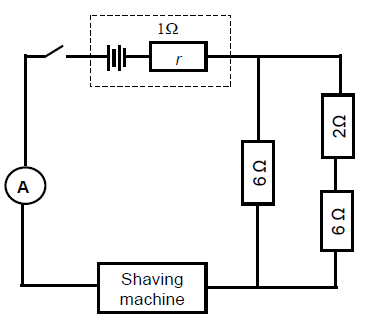
8.1 Calculate the effective resistance of the parallel network. (3)
8.2 The cost for operating the shaving machine for 5 hours per day over 5 days is R6,75. The price of electricity is R1,50 per unit (1 kWh).
Calculate the:
8.2.1 Power rating of the shaving machine (4)
8.2.2 Reading on the ammeter (3)
8.3 In order to save money, it was decided to use a battery since the machine can operate on direct current.
Calculate the:
8.3.1 Emf of the power source (battery) that should be used (5)
8.3.2 Resistance of the shaving machine (3)
[18]
QUESTION 9 (Start on a NEW page.)
The simplified diagram below represents a generator.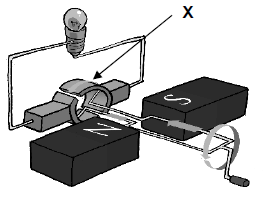
9.1 State the energy conversion that takes place while the generator is in operation. (2)
9.2 Write down the function of the component labeled X. (1)
9.3 Draw a graph of the induced emf versus time for ONE complete cycle for this type of generator. (2)
9.4 State ONE way in which the induced emf can be increased. (1)
[6]
QUESTION 10 (Start on a NEW page.)
A hair dryer is rated 2 000 W, 230 V.
10.1 Define root mean square voltage of an AC source. (2)
10.2 Calculate the maximum current that passes through the dryer when in use. (4)
[6]
QUESTION 11 (Start on a NEW page.)
The threshold frequency of a certain metal is 1,50 x 1014 Hz.
11.1 Define the term threshold frequency. (2)
11.2 Calculate the work function of the metal. (3)
11.3 Light with a wavelength of 540 nm is incident on the metal. Calculate the velocity of the ejected photoelectrons. (5)
11.4 Draw a graph that represents the relationship between the frequency and maximum kinetic energy of the emitted photoelectrons. Label the intercept of
the graph on the horizontal axis. (3)
[13]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES
PAPER 1 (PHYSICS)
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m•s-2 |
Universal gravitational constant | G | 6,67 x 10-11 N•m2•kg-2 |
Speed of light in a vacuum | c | 3,0 x 108 m•s-1 |
Planck's constant | h | 6,63 x 10-34 J•s |
Coulomb's constant | k | 9,0 x 109 N•m2•C-2 |
Charge on electron | e | -1,6 x 10-19 C |
Electron mass | me | 9,11 x 10-31 kg |
Mass of earth | M | 5,98 x 1024 kg |
Radius of earth | RE | 6,38 x 103 km |
TABLE 2: FORMULAE
MOTION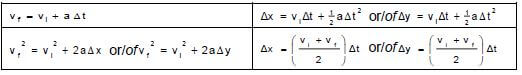
FORCE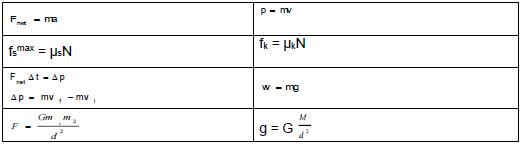
WORK, ENERGY AND POWER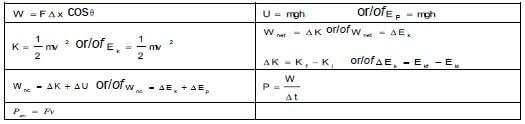
WAVES, SOUND AND LIGHT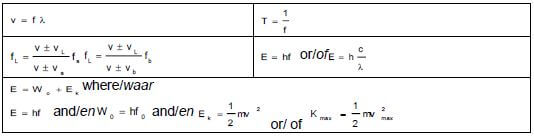
ELECTROSTATICS![]()
ELECTRIC CIRCUITS
ALTERNATING CURRENT
Mathematics P1 Grade 12 Errata - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
SUBJECT: GRADE 12 MATHEMATICS PAPER 1 ERRATA
- The Grade 12 Mathematics Paper 1 was written on Friday, 23 August 2019. The Directorate received reports from some schools and relevant stakeholders about some challenges experienced during the writing of Grade 12 Mathematics question paper.
- In order to address these challenges, the following standardised approach to marking should be adopted across the Province:
The word “repetition” and the fact that the word contains 2 x “R’s” contributed to the ambiguity of this question.
Below are solutions that may be considered for this examination ONLY.
QUESTION 11.2
11.2 Consider the letters of the word: NUMERATOR.
11.2.1 How many 9 letter word-arrangements can be formed, if repetition of letters is allowed? (1)
11.2.2 How many 9 letter word-arrangements can be formed, if all 4 vowels are never together and repetition of letters is not allowed? (3)
11.2.3 An 8 letter word-arrangement is made from the word NUMERATOR. All the vowels must be included in this word-arrangement and repetition of
letters is not allowed. What is the probability that all odd-number spaces are occupied by vowels? (4) [15]
| ORIGINAL MARKING GUIDELINE | ||
| 11.2.1 | 99 or 387 420 489 | √ 99 (1) |
| 11.2.2 | If vowels are together: 6! × 4! ∴ if vowels are not together: 9! - (6! × 4!) = 345 600 | √ 6! × 4! √ subtracting from 9! √ answer (3) |
| 11.2.3 | Vowels in odd spaces: = 4 × 5 × 3 × 4 × 2 × 3 × 1 × 2 = (4 × 3 × 2 × 1) × (5 × 4 × 3 × 2) = 4! × 120 = 2880 ∴ probability = 2880 (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2) = 2880 362880 = 1 126 | √ 4! × 120 √ vowels in odd spaces (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2) √ answer (4) [15] |
| CORRECTION TO MARKING GUIDELINE | ||
| 11.2.1 | Since there are only 8 distinct letters, the answer should be: 89 or 134 217 728 | √ 89 (1) |
| 11.2.2 | if vowels are together: OR The ambiguity might lead to the understanding that there are only 8 distinct letters but the word must contain 9 letters. NO SOLUTION | √ 6! × 4! 2! √ 9! 2! √ answer (3) |
| 11.2.3 | Since there are only 4 distinct consonants: ∴ probability = 576 | √ 4! × 4! √ vowels in odd spaces (8 × 7 × 6 × 5 × 4 × 3 × 2 × 1) √ answer (4) [15] |
After considering the impact of the ambiguity of the question, schools are informed not to mark this sub-question 11.2 and mark out of 142.
Mathematics P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
MARKING SCHEME
| QUESTION 1 | |||
| 1.1 | x = 420,8 80 = 5,26 | √ 420,8 80 √ answer | (2) |
| 1.2 | total of heights = 4,86 × 7 = 34,02 error = 4,98 - 4,89 = 0,09 new total heights = 33,93 new mean = 33,93 = 4,85m 7 | √ error = 0,09 √ new total √ answer | (3) |
| 1.3 | Standard deviation of individual heights of the 80 giraffes would be bigger than that of 7 males. There is a bigger spread of heights among population of juveniles and adults and babies. | √ bigger/larger standard deviation √ bigger spread of heights | (2) |
| [7] | |||
| QUESTION 2 | |||
| 2.1 | 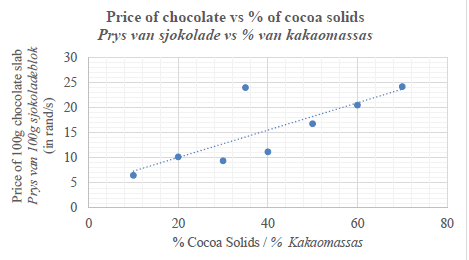 | √√ all points plotted correctly | (2) |
| 2.2 | y = a + bx a = 4,64 b = 0,27 y = 4,64 + 0,27x | √ value of a √ value of b √ equation | (3) |
| 2.3 | see line in 2.1 | √ correct gradient √ correct line | (2) |
| 2.4 | r = 0,78 | √ r = 0,78 | |
| 2.5 | fairly strong positive correlation in the % of cocoa and the price | √ correct description of r | (1) |
| 2.6.1 | Brand D OR (35;24) | √ answer | |
| 2.6.2 | y = 4,64 + 0,27(35) =R14,09 Overpriced by .R24,00 - R14,09 = R9,91 | √ substitution √ R14,09 √ R9,91 | (3) |
| [13] | |||
| QUESTION 3 | |||
| 3.1 | D(4;0) | √ answer | (1) |
| 3.2 | 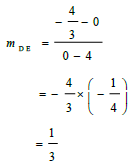 | √ substitution √ answer | (2) |
| 3.3 | Angle of inclination of DE = tan -11/3 = 18,43º ODE = 18,43º (vert.opp. ∠ s) OED = 71,57º (complementary ∠ s) ∴ PRB = 71,57º (corr. ∠ e: DE II BC) | √ tan -11/3 √ 18,43º √ answer √ reason | (4) |
| 3.4 | 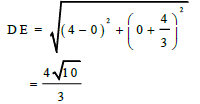 | √ substitution √ answer | (2) |
| 3.5 | AD = 3 = 1 AB 9 3 | √ ratios √ simplified answer | (2) |
| 3.6 | ΔABC III ΔADE OR equation of BC equation of AC | √ ratio of corresponding sides
OR √ equation of BC √ equation of AC | (3) |
| 3.7.1 | midpoint of DE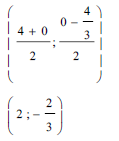 | √√ coordinates | (2) |
| 3.7.2 | mbisector = -3 Equation of bisector 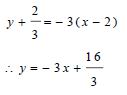 | √ gradient of bisector √ substitution √ equation | (3) |
| 3.8 | LHS = -3 RHS = -3(4) + 16/3 = - 20/3 = -62/3 ≈ -6,66 LHS # RHS No, bisector does not pass through A | √ substitution √ conclusion | (2) |
| [21] | |||
| QUESTION 4 | |||
| 4.1 | x2 - 6x + y2 = 16 (x - 3)2 + (y - 0)2 = 16 + 9 (x - 3)2 + (y - 0)2 = 25 Hence centre (3;0) Radius = √25 = 5 | √ completing the square √ final form √ taking square root | (3) |
| 4.2.1 | y = 0 : hence (x - 3)2 = 25 x - 3 = ± 5 x = 3 ± 5 B (8 ; 0) OR 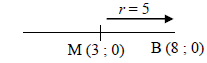 | √ equating = 0 OR √√√ use of horizontal distance | (3) |
| 4.2.2 | x = 0 : then (-3)2 + y2 = 25 OR using pythagoras : | √ equating x to 0 √ coordinates of C OR √ use of pythagoras √ coordinates of C | (2) |
| 4.3 | MCP = 90º OR POC = 90º | √ radius ⊥ tangent
| (3) |
| 4.4 |
OR
OR tan DBO = 4 = 1 | √ gradient of BD √ calculation of α √ angle θ √ doubling the angle OR √ sin definition √ use of arcsin √ angle θ √ doubling the angle OR √ tan ratio √ use of arctan to find angle √ angle √ doubling the angle | (4) |
| 4.5 | New circle centre OR Gradient of MC = 4/3 | √ coordinates of M and C OR √ gradient of MC | (4) |
| [19] | |||
| QUESTION 5 | |||
| 5.1.1 | 1 | √ answer | (1) |
| 5.1.2 | cos 2A | √ answer | (1) |
| 5.2.1 | 32 = 22 + k2 k = -√5 | √ distance formula pythagoras Thm √ answer with correct sign | (2) |
| 5.2.2 (a) | tan (θ -180º) tan θ = -√5 2 | √ reduction √ answer | (2) |
| 5.2.2 (b) |
OR
| √ 1 – sin22θ = cos2 2θ √ sin22θ = (2sinθcosθ)2 √ substitution for sin θ √ substitution for cos θ √ answer | (4) |
| 5.3 | sin (−200º).cos 310º + tan (−135º).cos 380º .sin 230º = sin (20º)(cos 50º) + (tan45º)(cos 20º)(−sin50º) = sin 20º cos 50º – (1)cos 20º sin 50º = sin (20º – 50º) = sin ( − 30º) = − ½ | √√√√ reductions to acute angles √ sin expansion √ answer | (6) |
| 5.4 | LHS= sin 2? + cos (2? – 90o) = sin 2? + sin 2? = 2 sin 2? = 2(2sin ? cos ?) = 4 sin ? cos ? = RHS/RK | √ cos (2θ – 90º) = sin 2θ √ simplification √ expansion | (3) |
| 5.5 | 10sin? + 10sin?.101=110 10sin?(1+10)=110 10sin?=101 ∴ sin x = 1 ∴ x = − 270º or/of x = 90º | √ split into product of 2 bases √simplification / factorisation √division by 11 √ equating the exponents √ both solutions | (5) |
| [24] | |||
| QUESTION 6 | |||
| 6.1 | 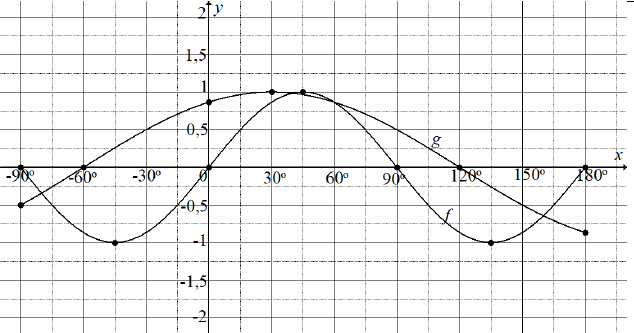 | √ completing f(x) = sin 2x graph | (1) |
| 6.2 | See graph in 6.1 | g(x) = cos (x – 30º) √ y intercept √ end points √ turning point √x intercepts | (4) |
| 6.3 | sin 2 x = sin (90º – ( ? – 30º)) sin 2 ? = sin (120º – ?) 2 ? = 120º − ? + k.360º or/of 2 ? = 180º – (120º − ?) + k. 360º 3 ? = 120º + k. 360º or/of ? = 60º + k. 360º ∴ ? = 40º + k. 120º or/of ? = 60º + k. 360º ; k ? Z k = 0 : ? = 40º ; 60º k = − 1 : ? = – 80º | √ co-ratio on RHS √ simplification √√ = 40º + k. 120º √ x = 60º + k. 360º √√ solutions | (6) |
| [11] | |||
| QUESTION 7 | |||
| 7.1 | tan y = PB | √ use of tan ratio √ PB = k.tan y √ BC = PB tan x | (3) |
| 7.2 | (AC)2 = (4,73)2 + (3)2 – 2(4,73)(3)( cos 100º) AC = 6,03 m | √ use of cosine rule √correct substitution in cosine rule √ answer | (3) |
| [6] | |||
| QUESTION 8 | |||
| 8.1.1 | BÂE = 90º ( ∠ in a semi-circle ) | √ statement / S √ reason / R | (2) |
| 8.1.2 | Ê1 = 40º ( sum of ∠ s of Δ ) | √ statement / S √ reason / R | (2) |
| 8.1.3 | C1 = 40º (∠s subtended by AB OR ∠s in the same segment) | √ statement / S √ reason / R | (2) |
| 8.1.4 | Ĉ2 = 62º (ext. ∠ of cyclic quad.) | √ statement / S √ reason / R | (2) |
| 8.1.5 | AB̂D = 62º (∠s subtended by AD OR ∠s in the same segment OR ext. ∠ of cyclic quad.) | √ statement / S √ reason / R | (2) |
| 8.2 | equal to the angle in the alternate segment/ | √ answer | (1) |
| 8.3 | R.T.P / Te Bewys: STUR cyclic OR R̂2 = 180º – (x + y) (3 ∠ s Δ) | √ statement / S √ reason / R √ S & R √ S & R √ opp. ∠ s of quad, supplementary | (5) |
| 8.4 | PN = NQ = 8 units (line from the centre ⊥ chord) M P2 = 62 + 82 (Pyth. Theorem) ∴ MP = 10 units MP = RM = MT = 10 (radii) ∴ RT = 20 units | √ S & R √ S & R √ S & R √ answer | (4) |
| [20] | |||
| QUESTION 9 | |||
| 9.1.1 | AD = AC n (prop theorem; DC II EF) DE CF 12 = AC 3 5 20 = AC | √ S & R √ Substitution √ answer | (3) |
| 9.1.2 | AO = 10 (diagonals of a parallelogram bisect) | √ answer | (1) |
| 9.1.3 | 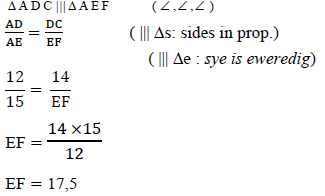 | √ S & R √ statement / S √ answer | (3) |
| 9.2 |  | (Area => Oppervlakte) OR √use of area rule | (3) |
| [10] | |||
| QUESTION 10 | |||
| 10.1 | 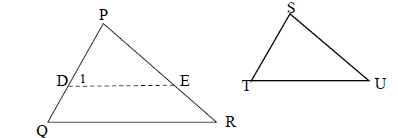 | (6) | |
| Construction: Mark D on PQ and E on PR such that PD = ST and PE = SU. Join DE. Proof: In ΔPDE and ΔSTU P ̂= Ŝ (given) PD = ST (construction) PE = SU (construction) ΔPDE ≡ ΔSTU (SAS) ∴ D̂1 = T ( ≡ Δ′?) But: Q̂ = T (given) ∴ D̂1 = Q̂ ∴ DE || QR (corr. ∠ s =) ∴ PD = PE (prop. theorem; DE || QR) PQ PR ∴ ST = SU PQ PR | √construction √ S & R √ D̂1 = T̂ √ D̂1 = Q̂ √ reason for lines∥ √ prop. theorem;DE || QR ;DE||QR | ||
| 10.2.1 | Â = x (tan chord thm) Ĉ3 = x (angles opp. = sides) | √ statement(S) √ reason(R) √ S & R | (3) |
| 10.2.2 | R.T.Ps: ΔTOC ⦀ Δ BPC ACB = 90º ( ∠ in the semi-circle) Proof : Ĉ3= Ĉ1 = ? (proved) T̂2 = 90º + ? (ext. ∠ of Δ) B̂1 = 90º + ? (ext. ∠ of Δ) ∴ T̂2 = B̂1 ∴ Ô2 = P̂ (sum of ∠ s in Δ) ∴ ΔTOC ⦀ Δ BPC (∠ , ∠ ,∠ ) OR ACB = 90º ( ∠ in the semi-circle) B2 = 90° − ? (sum of ∠s in Δ) ∴ P = 90° − 2? (ext. ∠of Δ) O1 = 2? (∠ at centre = 2 × ∠ at circum.) ∴ O2 = 90° − 2? (SO ⊥ AB) ∴ O2 = P ?3 = ?1 = ? (proved above) ∴ ΔTOC|||ΔBPC(∠, ∠, ∠) | √ S & R OR √ S & R | (5) |
| 10.2.3 | R.T.P : TO.PO = OB.BP Proof : TO = OC BP PC But OC = OB (radii) ∴ TO = OB BP PC ∴ TO.PC = OB.BP | √sides in prop. √ S | (2) |
| 10.2.4 | in ΔOPC: OP2 = OC2 + PC2 (pyth.theorem) But : OB = OC = BP (radii) ∴ (20C)2 = OC2 + PC2 4OC2 = OC2 + PC2 ∴ PC2 = 3OC2 | √ S & R √ OB = OC = BP √(2OC)2 = OC2 + PC2 | (3) |
| [19] | |||
| TOTAL: | 150 | ||
Mathematics P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
NOTE:
- If a candidate answers a question TWICE, mark the FIRST attempt ONLY.
- Consistent accuracy applies in ALL aspects of the marking guideline.
- If a candidate crossed out an attempt of a question and did not redo the question, mark the crossed-out attempt.
- The mark for substitution is awarded for substitution into the correct formula.
MARKING SCHEMES
| QUESTION 1 | ||
| 1.1.1 | x2 - 3x - 4 = 0 (x + 1)(x - 4) = 0 x = -1 or 4 Answerd only: (2/3) OR can use quadratic formula 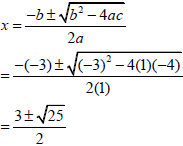 ∴ x = 4 or x = -1 | √ Factors √ x = -1 √ x = 4 √ correct substitution √ √ answers (3) |
| 11.2.2 | 2x2 - x - 7 = 0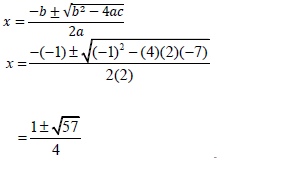 penalise 1 mark for incorrect rounding off x = 2,14 or -1,64 | √ substitution √ x = 2,14 √ x = -1,64 |
| 1.1.3 | 5x+1 - 5x = 2500 5x.51 - 5x = 2500 5x(5 - 1) = 2500 5x.4 = 2500 5x = 625 5x = 54 ∴ x = 4 | √ factorisation √ 5x = 625 √ x =4 |
| 1.1.4 | (x - 3)(x + 1) < 12 x2 - 2x - 3 - 12 < 0 x2 - 2x - 15 < 0 (x - 5)(x + 3) < 0 OR 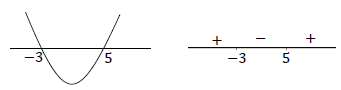 -3 < x < 5 OR x∈(-3;5) | √ standard form √ factorisation √√ -3 < x < 5 (accuracy) |
| 1.2 | y = 2x - 1 .......... (1) OR x = y + 1 .......(1) | √ y = 2x - 1
OR
√ x = y + 1 |
| 1.3 | f(x) = x2 - 2px + 8 + 2p OR b2 - 4ac = 0 | √ b2 - 4ac = 0
√ p values
√ b2 - 4ac = 0 |
| 2.1.1 | 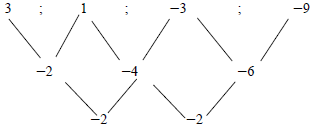 -17;-2 | √ both terms |
| 2.1.2 | 2a = -2 3a + b = -2 a + b + c = 3 ∴ a = -1 3(-1) + b = -2 -1 + 1 + c = 3 ∴ b = 1 ∴ c = 3 Tn = -n2 + n + 3 | √ a = -1 √ b = 1 √ c = 3 √ Tn = -n2 + n + 3 |
| 2.1.3 | -n2 + n + 3 = -809 n2 - n - 812 = 0 (n - 29)(n + 28) = 0 ∴ n = 29 | √ equating Tn to -809 √ factors √ choosing n = 29 |
| 2.2.1 | Tn = 2n - 3 T53 = 2(53) - 3 = 103 OR T53 = a + 52d = -1 + 52(2) = 103 | √ substitution into T53 √ answer √ substitution into T53 √ 103 |
| 2.2.2 | 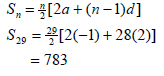 | √ substitution into correct formula √ 783 |
| 2.2.3 | √ √ 2n - 3 | |
| 2.3 | T4 = a + 3d and T10 = a + 9d ∴ T10 - T4 = 6d 6d = (8x - 2y) - (2x + y) = 6x - 3y ∴ d = x - ½y T4 = a + 3d 2x + y = a + 3(x - ½y) 2x + y = a + 3x - 3/2y ∴ a = 5/2y - x | √ T10 - T4 = 6d √ 6d = (8x - 2y) - (2x + y) √ d = x - ½y √ substitution √ value of a |
| QUESTION 3 | ||
| 3.1 | T1 = (x - 1) | √ -1 < r < 1 √ answer |
| 3.2 | When: 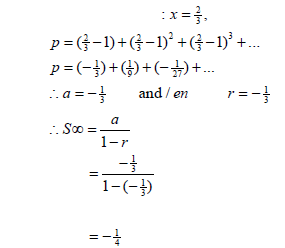 | √ substituting for x √ values for a and r √ substituting into S∞ formula √ answer |
| QUESTION 4 | ||
| 4.1 | x = -3 y = 1 | √ x = -3 √ y = 1 |
| 4.2 | 1 + 2 = 0 x + 3 2 = -1 x + 3 2 = -x - 3 x = -5 y = 1 + 2 0 + 3 = 5/3 | √ substitution √ x -intercept √ y-intercept |
| 4.3 | 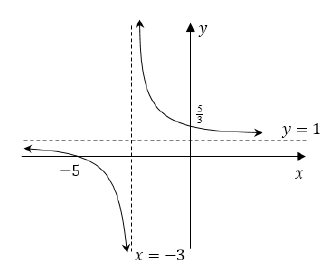 | √ asymptotes |
| 4.4 | h(x) = -2 - 1 OR h(x) = -2 - 1 | √ h(x) = -2 - 1
√ h(x) = -2 - 1 |
| QUESTION 5 | ||
| 5.1 | (0;-8) | √ answer |
| 5.2 | y = mx + c OR mTQ = 10 - (-8) | √ c = -8 √ substituting T(9;10) into equation of line √ equation |
| 5.3 | y = x2 - 7x - 8 = x2 - 7x + (-7/2)2 - 8 - (-7/2)2 = (x - 7/2)2 - 81/4 | √ completing the square √ equation |
| 5.4 | (7/2 ; -81/4) | √ x-coordinate √ y-coordinate |
| 5.5 | Ave gradient OR f'(x) = 2x - 7 | √ method
√ x2 - 7x - 8 - (10) = 1
√ equating to 1
|
| 5.6 | x2 - 7x - 8 = 0 ∴ x < -1 or 4 < x < 8 | √ x intercepts of f √ x intercept of g √ x < -1 accuracy √ 4 < x < 8 accuracy |
| QUESTION 6 | ||
| 6.1 | f(x) = logmx 3 = logm64 m3 = 64 m3 = 43 ∴ m = 4 | √ substitution √ answer |
| 6.2 | f(x) = log4x ∴ f-1 : x = log4x y = 4x | √ interchanging x and y √ answer |
| 6.3 | 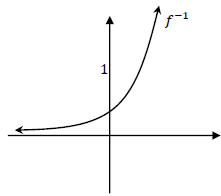 | √ y-intercept √ shape and asymptote |
| 6.4 | y > -2 OR y∈ (-2; ∞) | √ answer OR √ answer |
| QUESTION 7 | ||
| 7.1 | 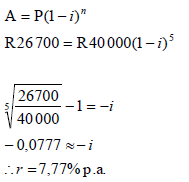 | √ substitution into correct formula √ simplification √ value for r |
| 7.2.1 | 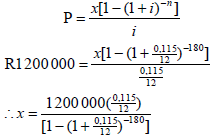 = R14 018,28 | √ i = 0.115/12 and n =180 √ substituting into correct formula √ answer |
| 7.2.2 (a) |
OR
= 2 453 828, 34 - 1528 392,76 Outstanding balance after 80 months; = 925 435,58 [1 + 11,5%]5 | √ ? = 105 for P and √ ? = 75 for both formulae
√ P(1 + 0,115)5 |
| 7.2.2 (b) | 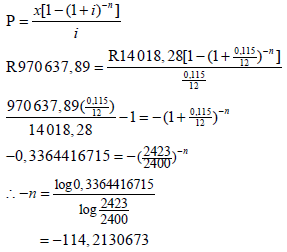 ∴ n = 115 months | √ P = R970 637,89 √ substituting into correct formula √ correct use of logs √ final answer |
| QUESTION 8 | ||
| 8.1 | 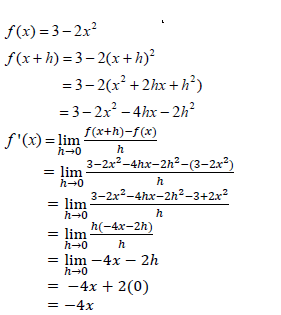 | √ 3 - 2x2 - 4hx - 2h2 √ substitution √ simplification √ factorisation √ answer |
| 8.2.1 | 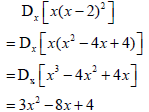 | √ x3 - 4x2 + 4x √ 3x2 √ - 8x √ +4 |
| 8.2.2 | 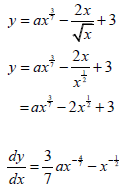 | √ -2x½ √ 3/7ax4/7 √ -x-½ (derivative of constant must be zero to get 3rd mark) |
| QUESTION 9 | ||
| 9.1 | x = -1/3 and x = 1 | √ x = -1/3 √ x = 1 |
| 9.2 | x = (1 + (-1/3)) ÷ 2 = 1/3 | √√ answer |
| 9.3 | g(x) is increasing when g'(x) > 0 -1/3 < x <1 OR x∈ (-1/3 ;1) | √√ answer |
| 9.4 |
OR
| √ substituting all intercepts
√ substituting all intercepts |
| 9.5 | g(x) = ax3 + bx2 + cx + d g'(x) = 3ax2 + 2bx + c = -3x2 + 2x + 1 ∴ 3a = -3 2b = 2 c = 1 ∴ a = -1 b = 1 ∴ y = -x3 + x2 + x + d + 1 0 = -03 + 02 + 0 + d + 1 ∴ d = -1 | √ g'(x) = 3ax2 + 2bx + c √ 3a = -3 √ 2b = 2 √ a = -1; b = 1; c = 1 √ substitute (0;0) into g(x) + 1 |
| QUESTION 10 | ||
| 10.1 | Let the two numbers be x and y : or y = 18 - 6 = 12 | √ x + y =18
|
| QUESTION 11 | ||
| 11.1.1 | a = 111 b = 106 | √ answer √ answer |
| 11.1.2 (a) | P(a boy who plays crickcet) = 108 or 54 530 265 | √ numerator √ denominator |
| 11.1.2 (b) | P(A or B) = P(A) + P(B) - P(A and B) OR P(girl or not tennis) | √ formula
√ method |
| 11.2.1 | 99 or 387 420 489 | √ 99 (1) |
| 11.2.2 | If vowels are together: 6! × 4! ∴ if vowels are not together: 9! - (6! × 4!) = 345 600 | √ 6! × 4! √ subtracting from 9! √ answer (3) |
| 11.2.3 | Vowels in odd spaces: = 4 × 5 × 3 × 4 × 2 × 3 × 1 × 2 = (4 × 3 × 2 × 1) × (5 × 4 × 3 × 2) = 4! × 120 = 2880 ∴ probability = 2880 (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2) = 2880 362880 = 1 126 | √ 4! × 120 √ vowels in odd spaces (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2) √ answer (4) [15] |
TOTAL: 150
Mathematics P2 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The table below shows the height, in metres, of 80 giraffes.
1.1 Calculate the estimated mean height of the giraffes. (2)
1.2 The height range of 4,8 ≤ ℎ < 5,0 m, consisted entirely of 7 young male giraffes. The mean of the heights of the 7 young males was calculated to be 4,86 m. However, it was noticed that the height of one of the young males was incorrectly recorded as 4,98 m but should have been 4,89 m. Calculate the new mean of the 7 young males. (3)
1.3 Would you expect the standard deviation of the individual heights of the 80 giraffes to be more or less than the standard deviation of the individual heights of the 7 young male giraffes? Explain your answer. (2) [7]
QUESTION 2
| Cocoa solids are used to make chocolate. A student is investigating the relationship between the percentage of cocoa solids in a 100g slab of chocolate and the price of the slab (in rands). The data obtained is shown in the table below. |  |
| chocolate brand | A | B | C | D | E | F | G | H |
| x (% of cocoa) | 10 | 20 | 30 | 35 | 40 | 50 | 60 | 70 |
| y (price in rand) | 6,50 | 10,20 | 9,40 | 24,00 | 11,20 | 16,80 | 20,50 | 24,20 |
2.1 Use the grid in the ANSWER BOOK to represent this data in a scatter plot. (2)
2.2 Determine the equation of the least squares regression line for this data. (3)
2.3 Draw the least squares regression line in the ANSWER BOOK on the same grid used in QUESTION 2.1. (2)
2.4 Calculate the correlation coefficient for the percentage of cocoa solids and the price of the chocolate slab. (1)
2.5 Comment on the relationship between the percentage of cocoa solids and the price of the chocolate slab. (1)
2.6 The student believes one brand of chocolate is overpriced.
2.6.1 Identify the chocolate brand which is over-priced. (1)
2.6.2 Estimate by how much more this slab of chocolate is overpriced. (3) [13]
QUESTION 3
In the diagram below, ∆ABC is shown with coordinates of A (4; – 3) and B (4 ; 6) given. AB intersects the x-axis at D and AC intersects the y-axis at E.
The coordinates of E are ![]() . BC intersects the y-axis at R. P is a point on the y-axis.
. BC intersects the y-axis at R. P is a point on the y-axis.
DE ∥ BC.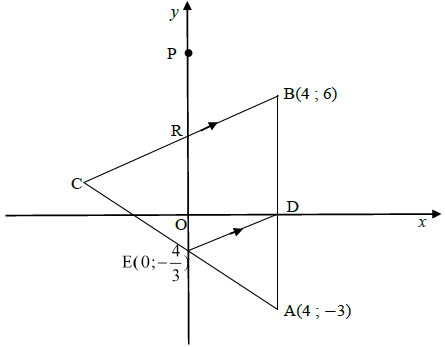
3.1 Write down the coordinates of D. (1)
3.2 Determine the gradient of DE. (2)
3.3 Calculate PR̂B. (4)
3.4 Calculate the length of DE in simplest surd form. (2)
3.5 Determine the ratio AD: AB in its simplest form. (2)
3.6 Hence, or otherwise, calculate the length of BC. (3)
3.7 Determine:
3.7.1 The midpoint of DE (2)
3.7.2 The equation of the perpendicular bisector of DE in the form y = mx + c (3)
3.8 Does this perpendicular bisector pass through A? Justify your answer. (2) [21]
QUESTION 4
The diagram below shows a circle having centre M which intersects the x-axis at A and B and the y-axis at D and C. PCQ is a tangent to the circle at C, the point of contact on the y-axis. P lies on the x-axis.
The equation of the circle is: x2 + y2– 6x – 16 = 0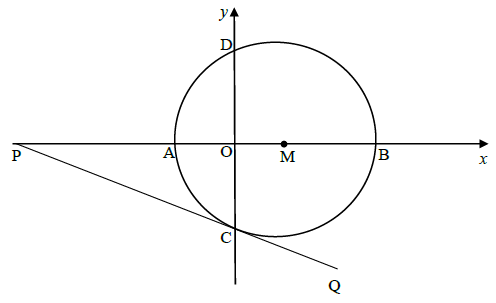
4.1 Show that the coordinates of M are (3; 0) and that the radius is 5 units. (3)
4.2 Determine:
4.2.1 The coordinates of B (3)
4.2.2 The coordinates of C (2)
4.3 If the length of PM is 81/3 units, calculate the length of PC. (3)
4.4 Calculate the angle subtended by the chord DC at B, i.e. find DB̂C. (4)
4.5 If the given circle is moved 2 units right and 1 unit up, determine the equation of the tangent to the circle in its new position passing through point C'. (4) [19]
QUESTION 5
DO NOT USE A CALCULATOR FOR THIS QUESTION.
5.1 Complete the following identities:
5.1.1 cos 2 A + sin 2 A = … (1)
5.1.2 cos 2 A − sin 2 A = … (1)
5.2 P(2 ; k) is a point in the Cartesian plane such that OP = 3 units and reflex angle TÔP = θ, as shown in the diagram below,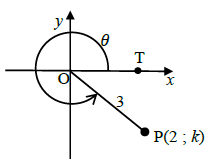
5.2.1 Calculate the value of k (leave your answer in surd form). (2)
5.2.2 Hence, determine the value of the following:
- tan (θ – 180º) (2)
 (4)
(4)
5.3 Determine, without the use of a calculator, the value of:
sin (−200º).cos 310º + tan (−135º).cos 380º.sin 230º (6)
5.4 Prove the following identity:
sin 2θ + cos (2θ – 90º) = 4 sin θ cos θ (3)
5.5 Solve for x if:
10 sin x + 10 sin x + 1 = 110 for − 360º ≤ x ≤ 360º (5) [24]
QUESTION 6
The graph below shows part of the function f (x) = sin 2x for 0º ≤ x ≤ 180º.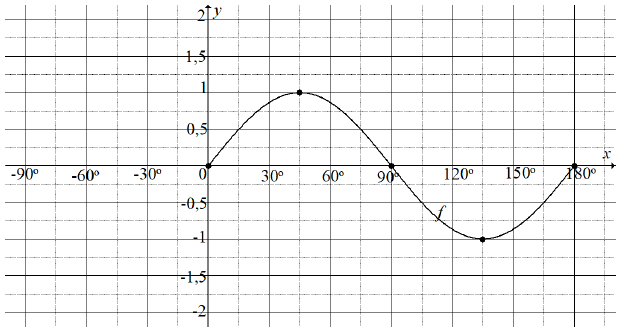
6.1 On the grid provided in the ANSWER BOOK, complete the graph of f for the interval − 90º ≤ x ≤ 180º. (1)
6.2 On the same grid, draw the graph of g (x) = cos (x – 30º) for the interval − 90º ≤ x ≤ 180º. Clearly show the intercepts with the axes, the coordinates of the turning points and the end points of the graph. (4)
6.3 Calculate the solutions to the equation:
sin 2x = cos (x – 30º) for – 90º ≤ x ≤ 90º(6) [11]
QUESTION 7
The diagram below shows a vertical netball pole PB. Player A is standing on the base line of the court and the angle of elevation from A to the top of the pole P is yº. A second player is standing in the court at C, and the angle of elevation from C to P is xº. Points A, B and C are in the same horizontal plane. BA is k metres; AB̂C = 100º.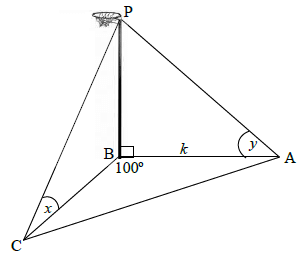
7.1 Show that BC = k.tan y (3)
tan x
7.2 Calculate the length of AC if BC = 4,73 m and k = 3 m. (3) [6]
Give reasons for your statements in QUESTIONS 8, 9, and 10.
QUESTION 8
8.1 In the given diagram, A, B, C, D and E are points on the circle.
BE is a diameter. Ê3 = 62º and B̂1 = 50º.
BD produced meets AE produced at F.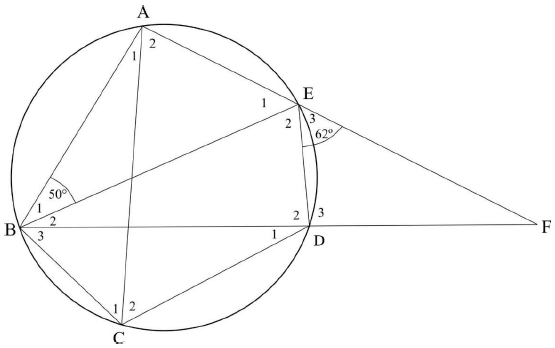
Determine, with reasons:
8.1.1 BÂE (2)
8.1.2 Ê1(2)
8.1.3 Ĉ1(2)
8.1.4 Ĉ2(2)
8.1.5 AB̂D (2)
8.2 Complete the following theorem statement: The angle between the tangent to a circle and the chord drawn from the point of contact is … (1)
8.3 In the diagram below, PRQ is a tangent to the circle SUR at R. SU, SR and UR are drawn. Lines from S and U produced meet at T outside the circle.
R̂1 = x ; Ŝ2 = y and ST̂U = x + y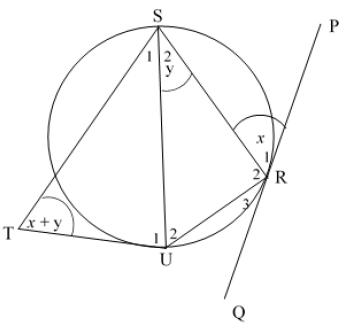
Prove that STUR is a cyclic quadrilateral. (5)
8.4 The diagram below shows a circle centre M passing through the points R, P, Q and T. RT is the diameter. PQ is a chord such that PQ ∥ RT and MN ⊥ PQ.
PQ = 16 units, MN = 6 units.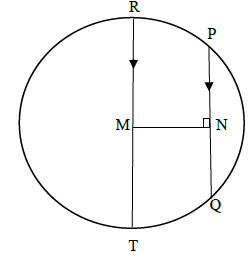
Determine the length of RT. (4) [20]
QUESTION 9
In the diagram below, ABCD is a parallelogram. AD and AC are produced to E and F respectively so that EF ∥ DC. AF and DB intersect at O.
AD = 12 units; DE = 3 units; DC = 14 units; CF = 5 units.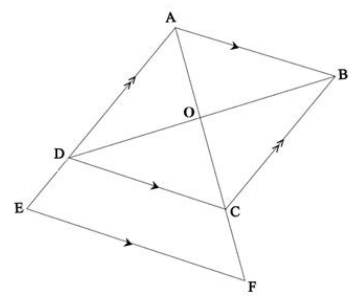
9.1 Calculate, giving reasons, the length of:
9.1.1 AC (3)
9.1.2 AO (1)
9.1.3 EF (3)
9.2 Prove that area 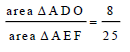 (3) [10]
(3) [10]
QUESTION 10
10.1 For the triangles shown below,
prove that if P̂ = Ŝ and Q̂ = T̂ and R̂ = Û then
ST = SU (6)
PQ PR
10.2 In the diagram below, O is the centre of a semi-circle ACB. S is a point on the circumference and T lies on AC such that STO ⊥ AB. Diameter AB is produced to P, such that PC is a tangent to the semi-circle at C. Let Ĉ1 = x.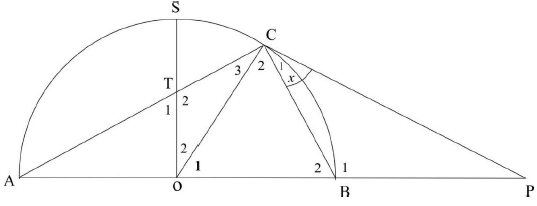
10.2.1 Write down, with reasons, 2 other angles equal to x. (3)
10.2.2 Prove that ∆TOC ⦀ ∆BPC (5)
10.2.3 Prove that TO.PC = OB.BP (2)
10.2.4 If BP = OB, show that 3OC2 = PC2(3) [19]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS

Mathematics P1 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of ELEVEN questions. Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answer.
- You may use an approved scientific calculator (non-programmable and non graphical), unless stated otherwise.
- Answers only will NOT necessarily be awarded full marks.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- Number the answers correctly according to the numbering system used in this question paper.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 x2 - 3x − 4 = 0 (3)
1.1.2 2x2 − x − 7 = 0 (correct to TWO decimal places) (3)
1.1.3 5x+1 − 5x = 2500 (3)
1.1.4 (x − 3)(x + 1) < 12 (4)
1.2 Solve the following equations simultaneously:
2x = y + 1
3x2 − xy − y2 = 1 (6)
1.3 Given that ƒ(x) = x2 − 2px + 8 + 2p has two equal roots and p < 0, determine the coordinates of the turning point of h, if h(x) = f (x) – 3. (5) [24]
QUESTION 2
2.1 Given the quadratic number pattern: 3 ; 1 ; −3 ; −9 ; …
2.1.1 Write down the next 2 terms of the pattern. (1)
2.1.2 Determine Tn, the ntℎ term of the pattern, in the form Tn = an2 + bn + c. (4)
2.1.3 Which term of the pattern has a value of −809? (3)
2.2 Given the arithmetic sequence: −1 ; 1 ; 3 ; 5 ; …
2.2.1 Determine T53, the 53rd term of the sequence. (2)
2.2.2 Determine the sum of the first 29 terms of the sequence. (2)
2.2.3 Hence, write your answer in sigma notation. (2)
2.3 In an arithmetic sequence, T4 = 2x + y and T10 = 8x − 2y. Determine the first term of the sequence in terms of x and y. (5) [19]
QUESTION 3
Given that: 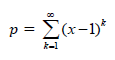
3.1 Determine the values of x for which p converges. (2)
3.2 Calculate the value of p when x = 2/3 (4) [6]
QUESTION 4
Given: ![]()
4.1 Write down the equations of the asymptotes of ƒ. (2)
4.2 Calculate the x and y intercepts of ƒ. (3)
4.3 Draw a neat sketch of ƒ, clearly indicating all intercepts with the axes and any asymptotes. (4)
4.4 Given that h is a reflection of f in the x-axis, determine the equation of the axis of symmetry of h having a positive gradient. (4) [13]
QUESTION 5
The diagram below shows the graphs of ƒ(x) = x2 − 7x − 8 and g(x) = mx + c. P and R are x-intercepts of ƒ, and V is the x-intercept of g. S is the turning point of ƒ. ƒ and g intersect on the y-axis at Q and also at T(9; 10).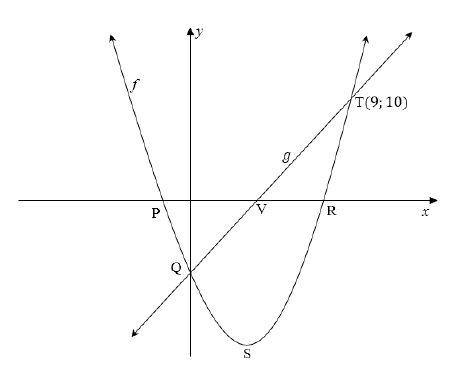
5.1 Write down the coordinates of Q. (1)
5.2 Determine the equation of g. (3)
5.3 Write down the equation of f in the form y = a(x + p)2 + q. (2)
5.4 Hence, or otherwise, determine the coordinates of S, the turning point of f. (2)
5.5 Determine the coordinates of a point W, on f , such that the average gradient between T and W is 1. (5)
5.6 Determine the values of x for which ƒ(x). g(x) < 0. (4) [17]
QUESTION 6
Given: ƒ(x) = logmx
6.1 Determine the value of m, if the point (64;3)lies on ƒ. (2)
6.2 Determine the equation of ƒ−1 in the form y =… (2)
6.3 Draw a neat sketch of ƒ−1, showing all intercepts with the axes. Indicate at least one other point on your graph. (2)
6.4 Write down the range of h if: ℎ(x) = ƒ−1(x) − 2 (1) [7]
QUESTION 7
7.1 Kamva bought a motorbike valued at R40 000. After 5 years the value of the motorbike had depreciated to R26 700, at a rate of r % p.a. on the reducing balance method, compounded annually. Calculate r, the rate of depreciation. (3)
7.2 A bank granted Nathan a loan for R1 200 000 to buy a house. He agreed to repay the loan over a period of 15 years at an interest rate of 11,5% p.a. compounded monthly. He made his first payment at the end of the first month after the loan was granted.
7.2.1 Calculate Nathan’s monthly instalment. (3)
7.2.2 Due to unforeseen circumstances, Nathan could not pay his 76th, 77th, 78th, 79th and 80th instalments. He resumed his payments at the end of the 81st month.
- Calculate the outstanding balance at the end of the 80th month. (5)
- If Nathan continues paying the same monthly instalment, how many months will it take him to pay the balance outstanding at the end of the 80th month? (4) [15]
QUESTION 8
8.1 Determine ƒ′(x) from first principles if ƒ(x) = 3 − 2x2(5)
8.2 Determine:
8.2.1 ![]() (4)
(4)
8.2.2 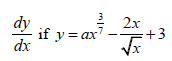 (3) [12]
(3) [12]
QUESTION 9
The diagram below shows the graph of y = g′(x) where g(x) = ax3 + bx2 + cx + d. The graph g′(x) cuts the y-axis at (0; 1) and the x-axis at (−13; 0) and (1; 0).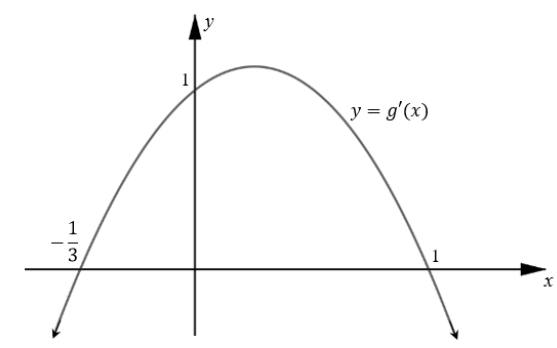
9.1 Write down the x-coordinate(s) of the stationary point(s) of g. (2)
9.2 Determine the x-coordinate of the point of inflection of g. (2)
9.3 Determine the values of x for which g is an increasing function. (2)
9.4 Determine the equation of g′(x) in the form: g′(x) = px2 + qx + r. (4)
9.5 Given that:
- g(x) + 1 passes through (0;0)and
- g′(x) = −3x2 + 2x + 1
Show that for g(x), a = −1, b = 1, c = 1 and d = −1. (5) [15]
QUESTION 10
Two numbers are such that their sum is 18. One of the numbers is multiplied by the square of the other. Calculate the numbers that make this product a maximum. [7]
QUESTION 11
11.1 A school has 530 learners. Each learner is expected to choose his/her summer extra-curricular activity from the following:
- Athletics
- Cricket
- Tennis
The choices for 2019 were recorded in the following partially completed table:
| Athletics | Cricket | Tennis | Total | |
| Girls | 120 | a | 57 | 288 |
| Boys | b | 108 | 28 | 242 |
| Total | 226 | 219 | 85 | 530 |
11.1.1 Determine the values of a and b. (2)
11.1.2 A learner is chosen at random. Determine the probability that:
- It is a boy who plays cricket (2)
- It is a girl or not a tennis player (3)
11.2 Consider the letters of the word: NUMERATOR.
11.2.1 How many 9 letter word-arrangements can be formed, if repetition of letters is allowed? (1)
11.2.2 How many 9 letter word-arrangements can be formed, if all 4 vowels are never together and repetition of letters is not allowed? (3)
11.2.3 An 8 letter word-arrangement is made from the word NUMERATOR. All the vowels must be included in this word-arrangement and repetition of letters is not allowed. What is the probability that all odd-number spaces are occupied by vowels? (4) [15]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS
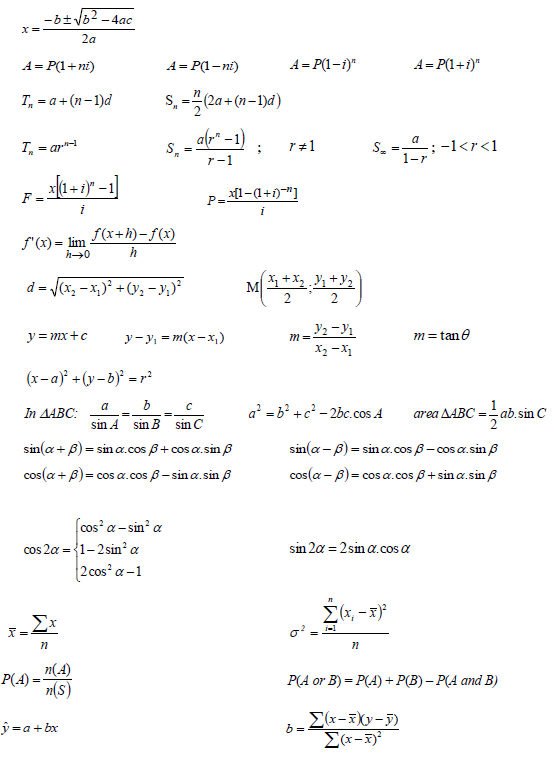
Technical Mathematics P1 Grade 12 Errata - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
The Technical Mathematics P1 Grade 12 September was written on Friday, 23 August 2019. We were made aware of certain amendments and omissions that were discovered during the marking process.
In order to address this and to ensure that learners are not disadvantaged, the following standardised approach to marking must be adopted across the Province. The following guidelines with regard to marking was prepared in conjunction with the examiner and moderator.
ERRATA
QUESTION 9
The driver of a motor car fills the petrol tank of his car to full capacity in a petrol station, to undertake a journey that requires a minimum of 25 ℓ of fuel to drive.
Unfortunately, he knocks his car on the corner of the road pavement as he leaves the petrol station resulting into a leakage from an opening in his petrol tank.
The picture below shows the damaged petrol tank of the car.
The equation, V(t) = t2 - 9t + 35 represents the amount of petrol lost over time in minutes t . ( )
Determine:
9.1 The amount of petrol in the tank before the leakage (2)
9.2 The amount of petrol that leaked out after 1 minute (2)
9.3 The time it took for maximum petrol to leak out of the tank (3)
9.4 The maximum amount of petrol that leaked (2) [9]
The original marking guideline:
| QUESTION 9 | |||
| 9.1 | V(t) = t2 - 9t + 35 V(0) = (0)2 - 9(0) + 35 = 35L | √substitution √V(0) = 35L | (2) |
| 9.2 | v(1) = t2 - 9t + 35 v(1) = (1)2 - 9(1) + 35 = 27L | √ substitution √ v(1) = 27L | (2) |
| 9.3 | v(t) = t2 - 9t + 35 v1(t) = 2t - 9 v1(t) = 2t - 9 = 0 t = 9/2 | √ v1(1) | (3) |
| 9.4 | maximum amount of fuel leaked | √ substitution √ V = 14,75L | (2) |
| [9] | |||
The statement is ambiguous; there are different interpretations of the statement given. The equation given has a minimum value, therefore to ask for the maximum petrol lost is not a possible option which makes Q.9.3 and Q.9.4 not valid. The recommendation is that QUESTION 9 should not be marked; thus the question paper total will be 141 marks when marking.
Technical Mathematics P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
MARKING CODES | |
M | Method |
MA | Method with accuracy |
A | Accuracy |
CA | Consistent accuracy |
S | Simplification or Statement |
R | Reason |
SR | Statement and correct reason |
SF | Substitution correctly in correct formula |
MARKING SCHEME
| QUESTION 1 | |||||||||||||||||||
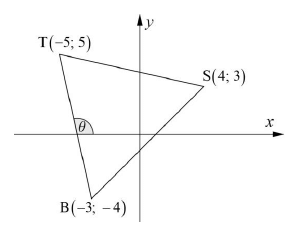 | |||||||||||||||||||
| 1.1 |  | √ SF √ S √ Length as a decimal | (3) | ||||||||||||||||
| 1.2 | mBT = y2 - y1 x2 - x1 = 5 + 4 - 5 + 3 = - 9 2 | √ SF √ S | (2) | ||||||||||||||||
| 1.3 | tan θ = mBT = - 9 2 θ = 180º - tan-1(9/2) =180º - 77,47º = 102,5º | √ SF √ S 180º - √ S 77,47º √ Value of θ | (4) | ||||||||||||||||
| 1.4 | y - y1 = m(x - x1) y - 3 = -9 (x - 4) 2 y = - 9x + 21 2 | √ gradient √ SF CA √ equation | (3) | ||||||||||||||||
| [12] | |||||||||||||||||||
| QUESTION 2 | |||||||||||||||||||
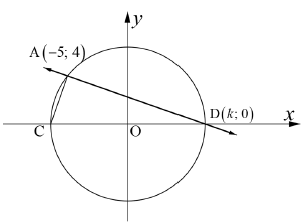 | |||||||||||||||||||
| 2.1 | x2 + y2 = (-5)2 + 42 = 25 + 16 = 41 | √ SF A √ equation | (2) | ||||||||||||||||
| 2.2 | x2 + 02 = 41 x = ± √41 ∴k = √41 | √ S A √ S CA √value of K | |||||||||||||||||
| 2.3 | mOA = 4 -5 | √ S | |||||||||||||||||
| 2.4 | mtangent = 5/4 ∴ equation of tangent y - y1 = m(x - x1) y - 4 = 5/4 (x + 5) y = 5/4 x + 41/4 | √ gradient CA √ SF CA √ equation | |||||||||||||||||
| 2.5 | mAD × mCA = 4 - 0 × 4 - 0 -5 - √41 -5 + √41 = 16 25 - 41 = 16 -16 = -1 ∴AD ⊥ CA (prod of grad = -1) OR AD2 = ( -5 - √41 )2 + (4 - 0)2 =25 + 10√41 + 41 + 16 = 82 + 10√41 C(-√41;0) AC2 = (-5 + √41)2 + (4 - 0)2 = 25 - 10√41 + 41 + 16 = 82 - 10√41 AD2 + AC2 = 82 + 10√41 +82 - 10√41 = 164 CD = CO + OD = √41 + √41 = 2√41 CD2 = 4 × 41 = 164 ∴ AD2 + AC2 = CD2 ∴ DAC = 90º (converse of pythagoras) No marks for angle in semicircle | √ gradients CA √ SF CA √ S CA √ R √ AD2 & AC2 CA √ AD2 + AC2 CA √ CD2 CA √ R | (4) | ||||||||||||||||
| [13] | |||||||||||||||||||
| QUESTION 3 | |||||||||||||||||||
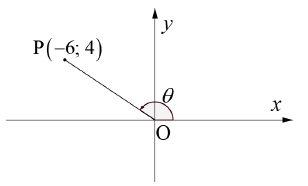 | |||||||||||||||||||
| 3.1.1 | 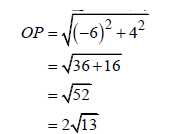 | √ applying pythagoras M √ value of OP | (2) | ||||||||||||||||
| 3.1.2 | 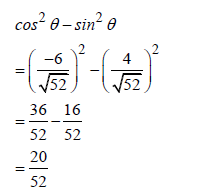 | √ value of cos θ CA | (4) | ||||||||||||||||
| 3.1.3 | cot θ - 2 = 4 - 2 -6 = - 8 3 | √ value of cot θ CA √ S CA | (2) | ||||||||||||||||
| 3.2 | 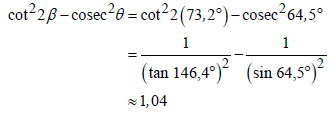 | √ SF A √ S 146,4º A √ 1 M tan 146,4º √ 1 M sin 64,5º √√ value CA | (6) | ||||||||||||||||
| 3.3 | 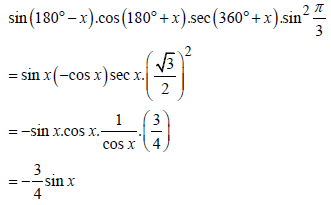 | √ sin x A √ -cos x A √ sec x A √ √3 A 2 √ I 1 A cos x √ ¾ C A √ -¾ sin x CA | (7) | ||||||||||||||||
| 3.4.1 | 4cos(2θ + 20º) = 2,178 cos(2θ + 20º) = 0,5445 2θ + 20º = 57º θ = 18,50º | √ S A √ S only 1st quadrant CA √ value of θ CA | |||||||||||||||||
| 3.4.2 | 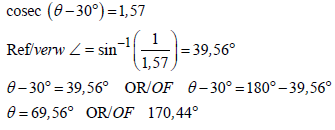 | √√ ref ∠ A √ 1st quad A √ 2nd quad A √ value quad 1 √ value quad 2 | |||||||||||||||||
| QUESTION 4 | |||||||||||||||||||
 | |||||||||||||||||||
| 4.1.1. | A: x = π = 90º 2 | √ S A | (1) | ||||||||||||||||
| 4.1.2 | P = 2 | √ S A | (1) | ||||||||||||||||
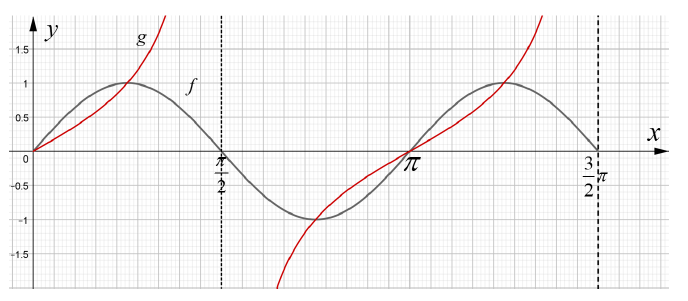
| 4.1.3 | Y = -1 | √ S A | (1) | ||||||||||||||||
| 4.2 | 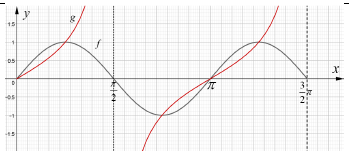 | √ Shape A (intercept at the turning points of f) √ x-intercept A √ asymptotes CA | (3) | ||||||||||||||||
| 4.3.1 | x∈{180º;225º} OR x∈{π; 5π} 4 | √ x= 180º = π CA √ x = 225º = 5π CA 4 | (2) | ||||||||||||||||
| 4.3.2 | x∈[0º;45º] = [0;π] 4 AND x∈(90º;135º) = (π ; 3π) 2 4 | √ critical values CA | (4) | ||||||||||||||||
| [12] | |||||||||||||||||||
| QUESTION 5 | |||||||||||||||||||
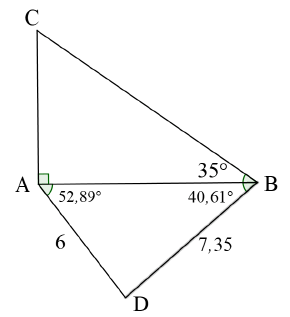 | |||||||||||||||||||
CA = tan 35º | √ S | (6) | |||||||||||||||||
| [6] | |||||||||||||||||||
| QUESTION 6 | |||||||||||||||||||
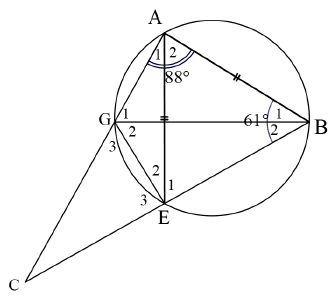 | |||||||||||||||||||
| 6.1 | E1 = 60º (∠s opp = sides) G1 = 61º (∠s in same seg) G3 = 61º (ext ∠ of cyclic quad) | √ SR √S√R √S√R | (5) | ||||||||||||||||
| 6.2.1 | E2 = 180º - 88º - 61º (opp ∠s of cyclic quad) = 31º | √S√R | (2) | ||||||||||||||||
| 6.2.2 | B1 = 31º (∠s in same segm) ∴ B2 = 30º | √S√R √S | (3) | ||||||||||||||||
| [10] | |||||||||||||||||||
| QUESTION 7 | |||||||||||||||||||
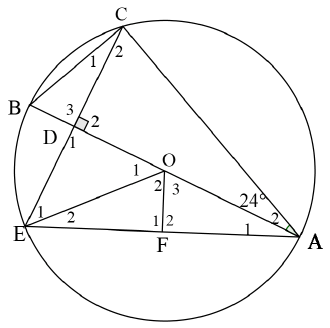 | |||||||||||||||||||
| 7.1 | C = 90º (∠in semi circle) B = 66º (int ∠s of Δ) | √ SR √S√R | (3) | ||||||||||||||||
| 7.2.1 | in ΔADC and ΔADE AD is common (line frm center ⊥ to chord) D1 = 90º = D2 ∴ΔADC = ΔADE (SAS) | √S √SR √ S √ R | (4) | ||||||||||||||||
| 7.2.2 | A1 = A2 (Ξ Δs) ∴ DA bisect | √ S | (1) | ||||||||||||||||
| 7.2.3 | O1 = 48º (∠ at centre = 2 × ∠ at circumf) | √S√R | (2) | ||||||||||||||||
| 7.3 | F2 = 90º (line from centre to midpoint of chord) ∴ DOFE is cyclic (converse ext ∠ of cyclic quad) | √S√R √R | (3) | ||||||||||||||||
| [13] | |||||||||||||||||||
| QUESTION 8 | |||||||||||||||||||
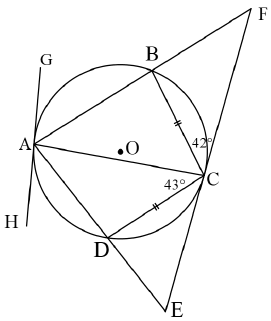 | |||||||||||||||||||
| 8.1.1 | BAC = 42º (tan-chord) DAC = 42º (equal chords; equal ∠s) | √S√R √S√R | (4) | ||||||||||||||||
| 8.1.2 | ADC = 95º (int ∠s of Δ) ABC = 85º (opp ∠s of cyclic quad) F = 43º (ext ∠ of Δ) | √S√R √S√R √S√R | (4) | ||||||||||||||||
| 8.2 | HAD = 43º (tan-chord) F = 43º (proved in 8.1.2) GAH a tangent to AFE (converse tan-chord th) | √S√R √R | (3) | ||||||||||||||||
| [11] | |||||||||||||||||||
| QUESTION 9 | |||||||||||||||||||
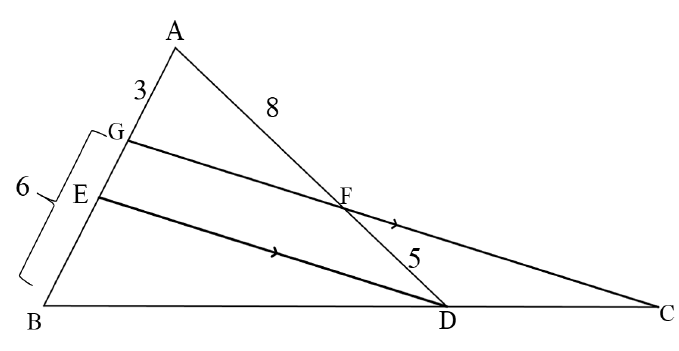 | |||||||||||||||||||
| 9.1 | let GE = x GE = FD (prop th; ED II GF) x = 5 3 8 x = 15 8 x = 1,875 x ≈ 2 | √S√R √S (ratio) √S (value of x) √S (rounding) | (5) | ||||||||||||||||
| 9.2 | In Δ GBC | √S√R √S CA (value of BE) √S value | (3) | ||||||||||||||||
| [8] | |||||||||||||||||||
| QUESTION 10 | |||||||||||||||||||
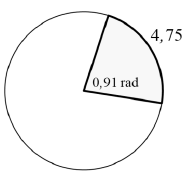 | |||||||||||||||||||
| 10.1.1 | s = rθ r = s θ = 4,75 0,91 = 5,22 cm | √ formula √ r subject √ SF A √ S CA | (4) | ||||||||||||||||
| 10.1.2 | circumference = 2πr = 2π(5,22) ≈ 32, 80 cm | √ formula A √ SF A √ S CA | (3) | ||||||||||||||||
| 10.2 | 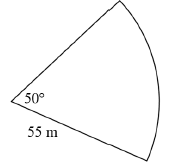 | ||||||||||||||||||
| 10.2.1 | 50º = 50º × π ≈ 0,873 rad 180º | √ M | (3) | ||||||||||||||||
| 10.2.2 | floodlit area = area of sector = ½ r2θ = ½ (55)2(0,873) ≈ 1320m2 | √formula √ SF √ S CA | (3) | ||||||||||||||||
| 10.3 | 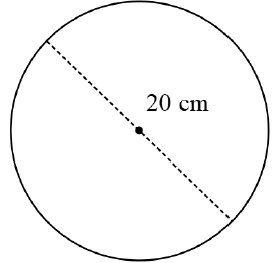 | ||||||||||||||||||
| 10.3.1 | r = 20 = 10 cm 2 | √ A | (1) | ||||||||||||||||
| 10.3.2 | n = 215 rev ϖ = 2πn = 2π (215) = 430 π rad | √ formula A √ SF A √ value of ϖ CA | (3) | ||||||||||||||||
| 10.3.3 | V = ϖr = 430π × 10 = 4300π cm/min | √ formula √ SF A √ value of v CA | (3) | ||||||||||||||||
| 10.3.4 | 4300π cm/min = 4300πcm × 60 min × 1 km 1 min 1 hr 10 000cm = 25,8 π ≈ 81 km/h | √ M × 60 √ M × 1 10 000 √ S CA √ rounding CA | (4) | ||||||||||||||||
| [24] | |||||||||||||||||||
| QUESTION 11 | |||||||||||||||||||
| |||||||||||||||||||
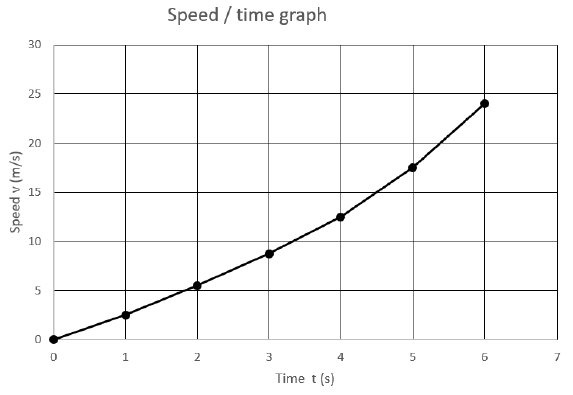 | |||||||||||||||||||
| 11.1 | 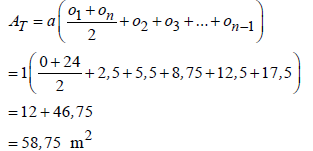 | √ formula A √ value of a A √ SF A √ value of AT CA | (4) | ||||||||||||||||
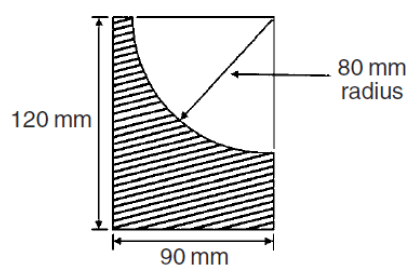 | |||||||||||||||||||
| 11.2 | Area of full rectangle = 1 × b Area of quater circle = 1/4πr2 Area of figure = 10800 - 1600π | ✓formula ✓SF A ✓ value of rectangle ✓formula ✓SF A ✓ value of circle ✓ value of figure | (7) | ||||||||||||||||
| [11] | |||||||||||||||||||
| TOTAL | 150 | ||||||||||||||||||