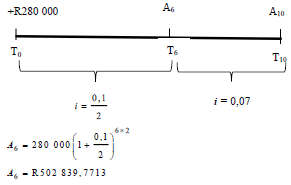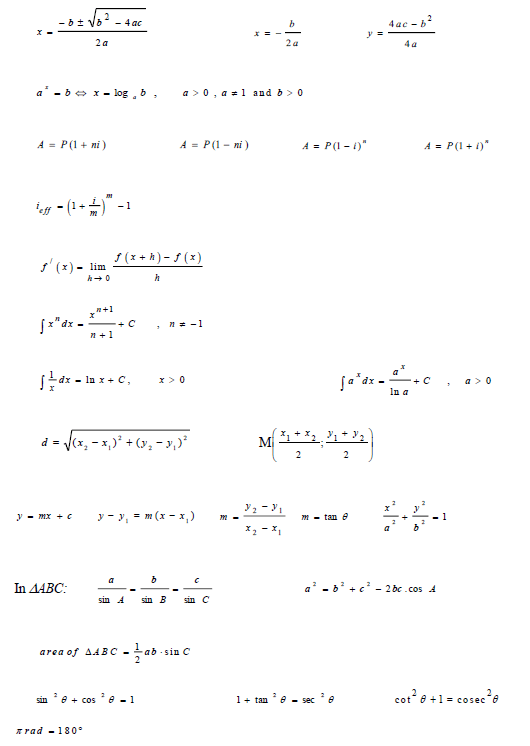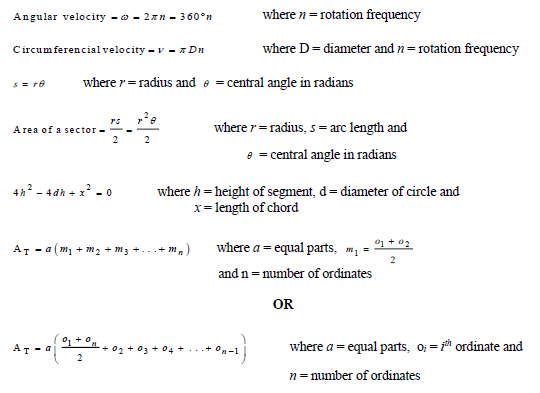Adele
Technical Mathematics P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
Marking Codes | |
A | Accuracy |
CA | Consistent accuracy |
M | Method |
R | Rounding |
NPR | No penalty for rounding |
NPU | No penalty for units omitted |
S | Simplification |
SF | Substitution in the correct formula |
AO | Answer only |
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- If a candidate has crossed out an attempt of a question and not redone the question, mark the crossed-out version.
- Consistent accuracy (CA) applies to ALL aspects of the marking guideline.
- Assuming answers/values to solve a problem is NOT acceptable.
| QUESTION 1 | ||||
| 1.1 | 1.1.1 | x(x - 5) = 6 x2 - 5x = 6 x2 - 5x - 6 = 0 (x - 6)(x + 1) = 0 x = 6 or x = -1 | √ Expansion √standard form √factors √x = 6 or x = -1 | (4) |
| OR | ||||
| x(x - 5) = 6 x2 - 5x = 6 x2 - 5x - 6 = 0 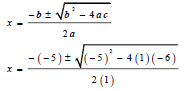 x = 6 or x = -1 | √expansion √standard form √substitution √x = 6 or x = -1 | |||
| 1.1.2 | -2x2 - 4x - 1 = 0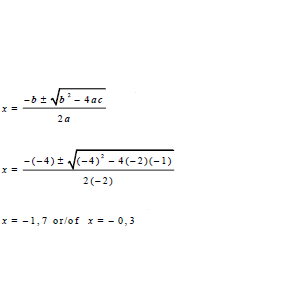 | √ formula √substitution √both values of x | (4) | |
| 1.1.3 | 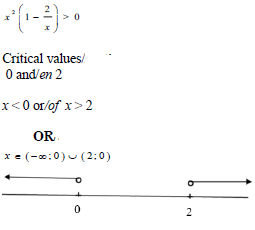 | √ critical values √ correct notation or √ number line | ||
| 1.2 | 1.2.1 | 20 seconds | √ 20 | (1) |
| 1.2.2 | 20 seconds = 20 hours 60 × 60 | √ 20 hours 60 × 60 | (1) | |
| 1.2.3 | 20 hours = 5,55 × 10-3 hours 60 × 60 | √Notation | (1) | |
| 1.3 | x/y = 2 ...............................(1) x2 + xy + y = 2 ..................(2) x = 2y ................................(3) Then (2y)2 + (2y)y + y = 2 4y2 + 2y2 + y - 2 = 0 6y2 + y - 2 = 0 (2y - 1)(3y + 2) = 0 | √ x- the subject √ substitution by √ simplification/std form √factors √ y-values √ x-values | (6) | |
| OR | ||||
| x/y = 2 ...............................(1) x2 + xy + y = 2 ..................(2) x/2 = y ................................(3) Then, x2 + x(x/2) + x/2 = 2 2x2 + x2 + x = 4 3x2 + x - 4 = 0 (3x + 4)(x - 1) = 0 x = -4/3 or x = 1 therefore: y = -2/3 or y = 1/2 | √ y-the subject √ substitute ; x/2 = y √ simplification / std form √factors √ x - values √ y- values | |||
| 1.4 | 1.4.1 | b = 2a = 2 × 2 = 4 | √ b = 4 √ c = 8 | (2) |
| 1.4.2 | b2 - 4ac = (4)2 - 4(2)(8) = 16 - 64 b2 - 4ac = -48 therefore; roots are non-real imaginary | √ Δ = -48 √ imaginary / non-real | (2) | |
| 1.5 | 41 = 1 × 25 + 0 × 24 + 1 × 23 + 0 × 22 + 0 ×21 + 1 × 20 -1 mark if base 2 is omitted | √ method √ 1010012 | (2) | |
| [26] | ||||
| 2.1 | 2.1.1 | 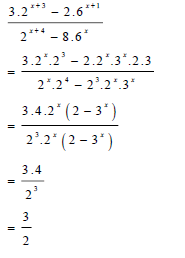 | √ Prime factors √ CF numerator √ CF denominator √ 3/2 | (4) |
| OR | ||||
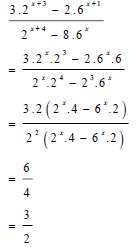 | √ same base √ CF numerator √ CF denominator √ 3/2 | |||
| 2.1.2 | 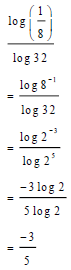 | √ log8-1 √ same base rule √ -3/5 | (3) | |
| OR | ||||
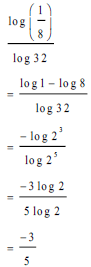 | √ log 1 - log 8 √ same base rule √ -3/5 | |||
| 2.2 | 2(x - y)(x - y) OR 2(x - y)(x + y) | √ substitution √ expansion √ simplification | ||
| 2.3 | 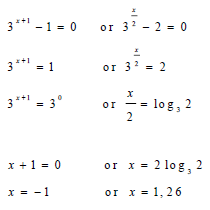 | √ 3x+1 = 1 √ 3x/2 = 2 √ 0 exponent rule √ log form 3x + 1 = 1 √ same base √ x = -1 3x/2 = 2 √ x = 2log32 √ x = 1,26 | ||
| OR | ||||
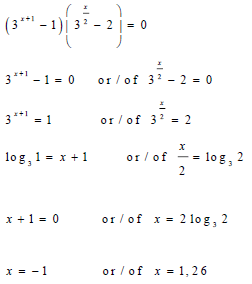 | √ 3x+1 = 1 √ 3x/2 = 2 √ log31 √ log32 √ x + 1 = 0 √ x = 2log32 √ x = -1 √ x = 1,26 | |||
| 2.4 | 3x = -3 and -5y = 0 x = -1 and y = 0 | √ equating parameters √ x = -1 √ y = 0 | ||
| 2.5 | 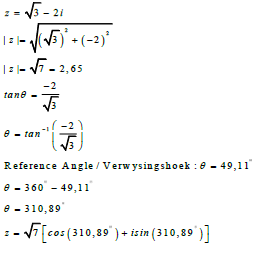 | √ finding r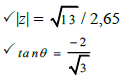 √ reference angle √ θ = 310,88º √ correct form | (6) | |
| [27] | ||||
| QUESTION 3 | ||||
| 3.1 | y = -4 | √ y = -4 | ||
| 3.2 | 3x - 4 = 0 3x = 4 x = log34 x = 1,26 | √ f(x) = 0 √ log form √ x = 1,26 | (3) | |
| 3.3 | f(x) = 3x - 4 f(0) = 3º - 4 y = -3 | √ subst. x = 0 √ y = -3 | (2) | |
| 3.4 | 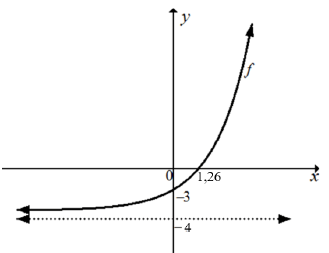 | √ shape √ both intercepts √ asymptote | (3) | |
| 3.5 | y > -4 or y∈(-4;∞) or -4<y<∞ | √ -4 | (1) | |
| [10] | ||||
| QUESTION 4 | ||||
| 4.1 | B(0;2) | √B(2;0) | (1) | |
| 4.2 | √ substitution √ g(x) = √4 - x2 | (2) | ||
| 4.3 | x∈[-2;2] OR -2 ≤ x ≤ 2 OR x ≥ -2 and x ≤ 2 | √ critical values from 4.1 √ notation | (2) | |
| 4.4 | x∈(-2;0) OR -2 < x < 0 | √ critical values from √ notation | (2) | |
| [7] | ||||
| QUESTION 5 | ||||
| 5.1 | h(0) = -(0)2 + 4(0) - 3 = -3 c(0;-3) | √ 0 √ -3 | (2) | |
| 5.2 | m(x) = p/x - 3 -1 = p/1 - 3 p = 2 | √ substitution √ p = 2 | (2) | |
| 5.3 | m(x) = 2/x - 3 | √ substitute 2 and -3 | (1) | |
| 5.4 | x = -b/2a = -4 2(-1) = 2 h(2) = -(2)2 + 4(2) - 3 = 1 D(2;1) | √ substitution √ x = 2 √ h(2) √ D(2;1) | (4) | |
| OR | ||||
| h'(x) = -2x + 4 = 0 therefore x = 2 h(2) = -(2)2 + 4(2) - 3 = 1 D(2;1) | √ h'(x) = -2x + 4 √ x = 2 √ h(2) √ D(2;1) | |||
| OR | ||||
| (-x + 1) (x - 3) = 0 x = 1 or x = 3 therefore axis of symmetry x = 1 + 3 = 2 2 h(2) = - (2)2 + 4(2) - 3 = 1 D(2;1) | √ x-intercepts √ x = 2 √ h(2) √ D(2;1) | |||
| 5.5 | DE = 1 + 3 = 4 units | √ OE + OD √ 4 | ||
| QUESTION 6 | ||||
| 6.1 | 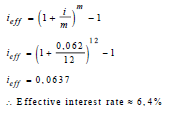 | √ formula √ substitution √ ieff ≈ 6.4% | ||
| 6.2 | A = P (1 - in) 40 000 = P(1 - 0,1 × 3) P = 40000 = R57 142,86 (1 - 0,1 × 3) | √ substitute i and n √ substitution √ P subject √ simplification | ||
| 6.3 |
A10 = R 352 839, 7713 (1 + 0,07)4 | √ values of i and n √ substitute P, i and n √ A6 √ P6 √substitution P6, i and n √ value of A10 | (6) | |
| OR | ||||
| A6 = R502 839, 7713 A6(1) = R 502 839, 7713 (1 + 0,07)4 A6(1) = R 659 120,3659 A7(1) = R 150 000(1 +0,07)4 A7(1) = R 196 619, 4015 A10 = R 659 120, 3659 - R 196 619, 4015 A10 = R 462 500, 96 | √values of i and n √ substitute P, i and n √ A6 √ P6 √ A6 √ P6 √ A 2(1) √ A6 √ P6 √ value of A10 | |||
| [13] | ||||
| QUESTIONS 7 | ||||
| 7.1 | 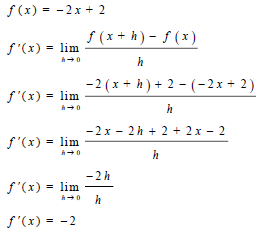 | √ definition √ substitution √ simplification √ simplification √ f'(x) = -2 | (5) | |
| 7.2 | 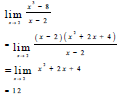 | √ (x - 2)(x2 + 2x + 4) √ simplification √ 12 | (3) | |
| 7.3 | 7.3.1 | y = - 3 - 2x2 + 2x 5x2 y = 3x-2 - 2x2 + 2x 5 dy = 6x-3 - 4x + 2 dx 5 | √ - 3 5x2 √ 6x-3 5 √ - 4x √ 2 | (4) |
| 7.3.2 | 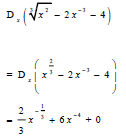 | √ x 2/3 √ 2/3x-1/3 √ 6x-4 | (3) | |
| [15] | ||||
| QUESTION 8 | ||||
| 8.1 | 8.1.1 | y = -4 | √ y = -4 | (1) |
| 8.1.2 | f(x) = (1 - 2x)(x2 - 4) 0 = (1 - 2x) (x2 - 4) x = ½ or x = 2 or x = -2 | √ f(x) = 0 √ x = ½ √ x = ± 2 | (3) | |
| 8.1.3 | f(x) = -2x3 + x2 + 8x - 4 | √ f(x) = -2x3 + x2 + 8x - 4 | (1) | |
| 8.1.4 | f(x) = -2x3 + x2 + 8x - 4 f'(x) = -6x2 + 2x + 8 0 = -6x2 + 2x + 8 0 = 3x2 - x - 4 0 = (x + 1) (3x - 4) x = 4/3 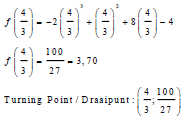 | √ f(x) CA from 8.3 √ f'(x) = 0 √ factors √ x = 4/3 √ [100] [ 27 ] | (5) | |
| 8.1.5 | 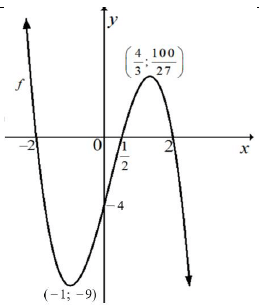 | √ x-intercept √ y-intercept √ turning points √ shape | (4) | |
| 8.2 | Average gradient = g(a) - g(4) = 9 a - 4 (2a2 - a - 3) - 25 = 9 a - 4 2a2 - a - 28 = 9a - 36 2a2 - 10a + 8 = 0 a2 - 5a + 4 = 0 (a - 4) (a - 1) = 0 a = 1 | √ g(a) - g(4) a - 4 √ = 9 √ STD form √ factors √ a = 1 | (5) | |
| [19] | ||||
| QUESTION 9 | ||||
| 9 | 9.1 | V(t) = t2 - 9t + 35 V(0) = (0)2 - 9(0) + 35 = 35L | √ substitution √ V(0) = 35L | (2) |
| 9.2 | V(t) = t2 - 9t + 35 V(1) = (1)2 - 9(1) + 35 = 27L | √ substitution √ V(1) = 27L | (2) | |
| 9.3 | V(t) = t2 - 9t + 35 V'(t) = 2t - 9 V'(t) = 2t - 9 = 0 t = 9/2 | √ V'(t) √ V'(t) = 0 √ t = 9/2 | (2) | |
| 9.4 | maximum amount of fuel leaked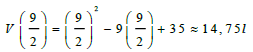 | √ substitution √ V ≈ 14,75L | ||
| QUESTION 10 | ||||
| 10.1 | √ x3 3 √ 3inx √ x √ c | |||
| 10.2 | 10.2.1 | 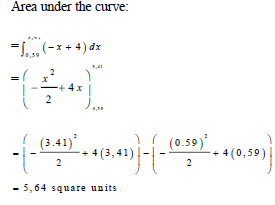 | √ integral function √ correct lower and upper bounds √ simplification √ substitute 3,41 √ substitute 0,59 √ 5,64 | (6) |
| 10.2.2 | Striped A = A under f (x) – A under g(x) Striped area =5,64−3,5 Striped area =2,13 square units | √ difference √ substitution √ 2,13 square units | (3) | |
| [13] | ||||
| TOTAL | 150 | |||
Technical Mathematics P2 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non graphical) unless stated otherwise.
- If necessary, round off your answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The picture below is of two tugboats pulling a ship into the harbour.
The diagram next to it is a representation of the situation, where S represents the ship and T and B, the tugboats.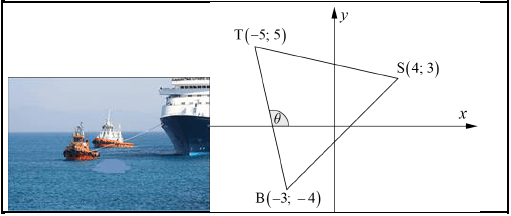
1.1 Calculate the length of ST, rounded off to TWO decimal places. (3)
1.2 Calculate the gradient of BT. (2)
1.3 Hence, calculate the size of θ with the positive x-axis, rounded off to ONE decimal place. (4)
1.4 Determine the equation of the straight line through S parallel to BT. (3) [12]
QUESTION 2
In the diagram below, circle ACD with centre O at the origin, cuts straight line AD at A (-5; 4) and D (k;0). D is on the x-axis.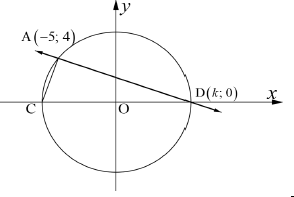
Determine:
2.1 The equation of the circle (2)
2.2 The numerical value of k (3)
2.3 The gradient of OA (1)
2.4 The equation of the tangent to the circle at A (3)
2.5 Analytically that DAC = 90º (4) [13]
QUESTION 3
3.1 In the diagram below, P is the point (−6; 4). θ is the angle between the x-axis and the straight line, OP.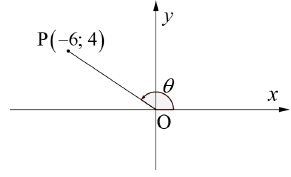
Calculate the numerical value of the following (leave your answer in surd form):
3.1.1 OP (2)
3.1.2 cos2θ - sin2θ (4)
3.1.3 cotθ − 2 (2)
3.2 If θ = 64,5° and β = 73,2°, calculate the following, correct to TWO decimal places (Show all your workings): cot22β - cosec2θ (6)
3.3 Simplify: sin (180º - x).cos(180º + x).sec(360º + x).sin2π/3 (7)
3.4 Solve for θ, give your answer correct to ONE decimal place:
3.4.1 4cos(2θ + 20º) = 2,178 (2θ + 20º)∈[0º;180º](3)
3.4.2cosec (θ - 30º) = 1,57 θ∈[0º; 360°) (6) [30]
QUESTION 4
Given f (x) = sin px and g(x) = tan x for ![]()
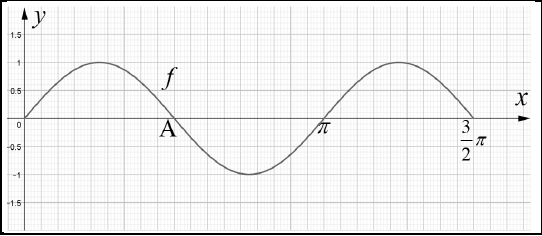
4.1 Write down:
4.1.1 The value of A (1)
4.1.2 The value of p (1)
4.1.3 The minimum value of f (1)
4.2 Draw the graph of g on the same system of axis as provided in your ANSWER BOOK. Clearly indicate ALL critical points. (3)
4.3 Use the graphs to determine for which value(s) of x is:
4.3.1 f(x) - g(x) = 0, where ![]()
4.3.2 f (x) ≥ g(x), where x∈[0; π ] (4) [12]
QUESTION 5
In the diagram below, A, B and D are three points in the horizontal plane. AC is a vertical tower and the angle of elevation from B to C is 35°.
- ABD = 40 61º
- BAD = 52 89º
- AD = 6 m and BD = 7,35 m
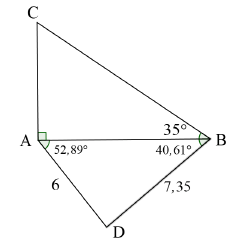
Determine the height of the tower CA, correct to ONE decimal place. (6) [6]
QUESTION 6
In the diagram below, ABEG is a cyclic quadrilateral with AB = AE and ABE 61 AG and BE are produced to meet at C.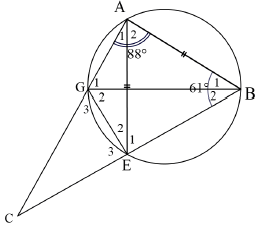
6.1 Name, with reasons, three other angles equal to 61°. (5)
6.2 If BAG = 88º, determine, stating reasons, the size of:
6.2.1 E2 (2)
6.2.2 B2 (3) [10]
QUESTION 7
In the diagram, the vertices of ΔACE lie on the circle with centre O.
- Diameter AB and chord CE intersect at D.
- DO ⊥ CE
- A2 = 24º
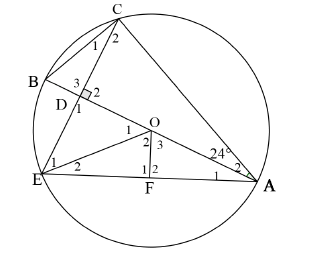
7.1 Determine, stating reasons, the size of Bˆ. (3)
7.2
7.2.1 Show that ΔADC ≡ ΔADE. (4)
7.2.2 Hence, show that DA bisect Aˆ. (1)
7.2.3 Determine, stating reasons, the size of O1ˆ.(2)
7.3 If it is further given that EF = FA, prove that DOFE is a cyclic quadrilateral. (3) [13]
QUESTION 8
In the diagram, ABCD is a cyclic quadrilateral with BC = CD.
- The tangent at C intersect with AB produced in F and AD produced in E.
- GAH is a tangent to the circle at A.
- BCF = 42°
- ACD = 43°
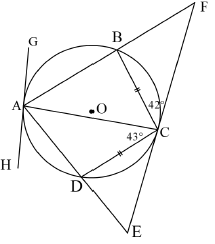
8.1 Determine, stating reasons, the size of: ˆ(4)
8.1.1 DAC (4)
8.1.2 F (4)
8.2 Prove that GAH is a tangent to circle AFE. (3) [11]
QUESTION 9
In the diagram below, side BD of ΔABD is produced to C.
- F is a point on AD so that AF = 8 and FD = 5.
- CF produced cuts AB at G so that AG = 3 and GB = 6.
- E is a point on GB such that ED || GC.
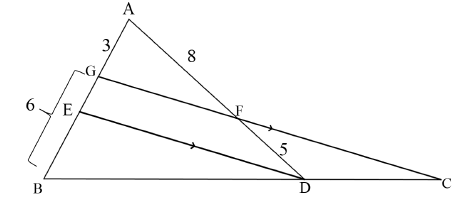
9.1 In ΔAED, determine the value of GE, with reasons, to the nearest integer. (5)
9.2 Determine, with reasons, the numerical value of BC/BD.(3) [8]
QUESTION 10
10.1 In the diagram below, an arc of length 4,75 cm subtends an angle of 0,91 radians.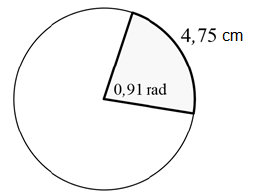
10.1.1 Determine the length of the radius of the circle. (4)
10.1.2 Hence, determine the circumference of the circle. (3)
10.2 A football stadium floodlight can spread its illumination over an angle of 50° to a distance of 55 m. Represented by the pictures and diagram below.
10.2.1 Convert 50° to radians, rounded off to THREE decimals. (3)
10.2.2 Determine the maximum area that is floodlit. (3)
10.3 A desk fan with diameter 20 cm is rotating 215 times every minute.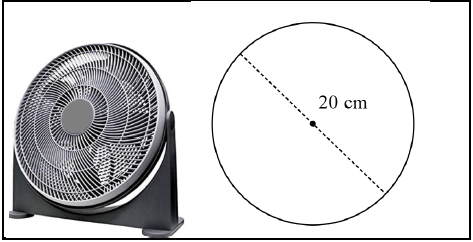
10.3.1 Calculate the length of a fin. (1)
10.3.2 Calculate the angular velocity. (3)
10.3.3 Calculate the linear speed of the fan. (3)
10.3.4 Determine the linear speed to the nearest km/h. (4) [24]
QUESTION 11
11.1 A car starts from rest and its speed is measured every second for 6 s. This data is represented in the table below.
| Time t(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Speed v (m/s) | 0 | 2,5 | 5,5 | 8,75 | 12,5 | 17,5 | 24 |
This data is further represented by a speed-time graph below.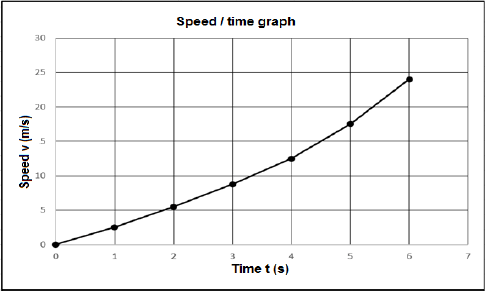
Determine the distance travelled in 6 seconds (i.e. the area under the speed-time graph) by the mid-ordinate rule. (4)
11.2 The picture below is of a Lego brick. The diagram next to it represents the Lego brick with measurements.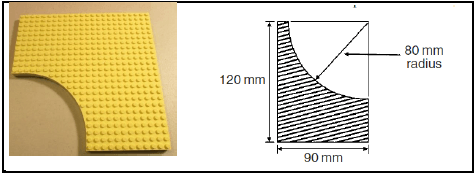
Determine the area of the Lego brick as shown in the diagram. (7) [11]
TOTAL: 150
INFORMATION SHEET
Technical Mathematics P1 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera, that you have used in determining your answers.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, ALL answers should be rounded off to TWO decimal places, unless stated otherwise.
- Number the answers correctly according to the numbering system used in this question paper.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is attached.
- Diagram sheets are attached for QUESTION 3.4 and QUESTION 8.1.5. Write your name in the spaces provided and hand in the diagram sheets with your ANSWER BOOK.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 x (x − 5) = 6 (4)
1.1.2 -2x2 - 4x - 1 = 0 (correct to ONE decimal place) (3)
1.1.3 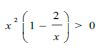 , also represent the solution on a number line.(4)
, also represent the solution on a number line.(4)
1.2 Diagram A below shows a ticker timer, tape and a trolley.
Diagram B shows the top view of the tape with the results recorded by the ticker timer on the tape, as dots.
Diagram A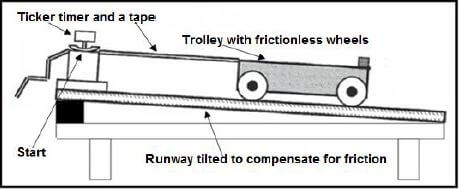
Diagram B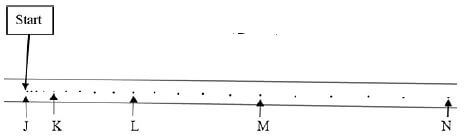
- Each dot on the tape corresponds to ONE second lapse by the timer.
- 5 dot intervals are indicated by points K, L, M and N from start position, J, in Diagram B.
1.2.1 How many seconds were recorded by the timer on the tape from J to N? (1)
1.2.2 Convert the time from J to N into hours. (1)
1.2.3 Hence, express the hours in QUESTION 1.2.2 in scientific notation. (1)
1.3 Solve the following equations simultaneously:
x = 2 and x2 + xy + y = 2 (6)
y
1.4 Given: 2x2 + bx + c = 0
1.4.1 If a = 1/2b and b= 1/2c calculate and evaluate the values of b and c. (2)
1.4.2 Hence, without solving the equation, describe the nature of roots of 2x2 + bx + c = 0 (2)
1.5 Write 41 as a binary number. (2) [26]
QUESTION 2
2.1 Simplify the following WITHOUT using a calculator:
2.1.1 ![]() (4)
(4)
2.1.2 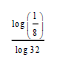 (3)
(3)
2.2 Given: x = √2 and y = √3
Determine, without using a calculator, the numerical value of 2(x - y)(x + y) (3)
2.3 Solve for x if: 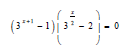 (8)
(8)
2.4 Solve for x and y if 3x - 5yi = -3 (3)
2.5 Write z =√3 - 2i in the form r (cos θ + isin θ) (6) [27]
QUESTION 3
Given: ƒ(x) = 3x - 4
3.1 Write down the equation of the asymptote of ƒ. (1)
3.2 Determine the x-intercept of ƒ. (3)
3.3 Determine the y-intercept of ƒ. (2)
3.4 Sketch the graph of ƒ on the ANSWER SHEET provided. Clearly show all the asymptotes and intercepts with the axes. (3)
3.5 Write down the range of ƒ. (1) [10]
QUESTION 4
In the diagram drawn below, is a linear function defined by f (x) = x + 2 and a semi-circle defined by g(x) = √r2 - x2
ƒ and g intersect at point A and B respectively.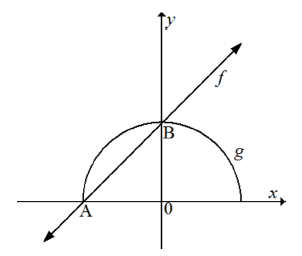
Determine:
4.1 The coordinates of point B (1)
4.2 The equation of the semi-circle, g (2)
4.3 The domain of g (2)
4.4 The value(s) of x for which ƒ(x) < g(x) and ƒ(x) >0 (2) [7]
QUESTION 5
The diagram below shows sketch graphs of functions defined by m(x) = p/x + q ; x # 0 and h(x) = -x2 + 4x - 3
A and B (1; − 1) are points on m(x) and h(x) cut the y-axis at C.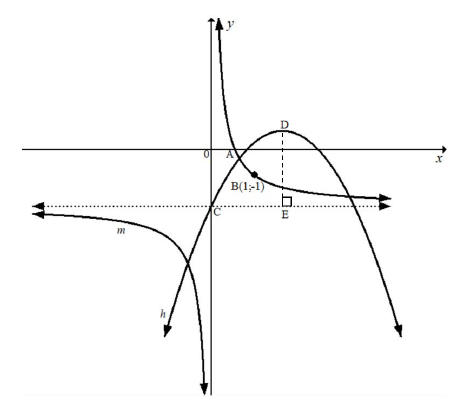
5.1 Determine the coordinates of C, the y-intercept of h. (2)
5.2 Determine the value of p. (2)
5.3 Write down the equation of m(x) (1)
5.4 Determine the coordinates of D, the turning point of h. (4)
5.5 Calculate the length of DE. (2) [11]
QUESTION 6
6.1 Determine the effective interest rate, compounded monthly, if the nominal interest rate is 6,2% per annum. (3)
6.2 A milling machine loses its value on a straight-line depreciation to R40 000 after 3 years. If the depreciation rate is 10% p.a., determine the original cost price of the machine. (4)
6.3 Water Drilling Project invested R280 000 for 10 years in an account to buy cash a borehole drilling machine, as shown in the picture below.
- The investment accumulates interest rate of 10% per annum, compounded half yearly for the first 6 years of the investment.
- After 6 years the company withdrew R150 000 from the investment account.
- The interest rate decreased from 10% to 7% per annum compound interest for the remaining 4 years of investment.
- The cost price of the borehole drilling machine is expected to be approximately R450 000 after 10 years.
Calculate how much money will be in the investment account after 10 years. (6) [13]
QUESTION 7
7.1 Determine the derivative of f(x) = -2x + 2 by using first principles. (5)
7.2 Evaluate: 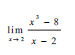 (3)
(3)
7.3 Determine:
7.3.1 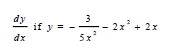 (4)
(4)
7.3.2 ![]() (3) [15]
(3) [15]
QUESTION 8
8.1 G iven : f(x) = (1 - 2x)(x2 - 4)
8.1.1 Write down the y-intercept of ƒ. (1)
8.1.2 Determine the x-intercepts of ƒ. (3)
8.1.3 Write ƒ(x) in the form of ƒ(x) = ax3 + bx2 + cx + d (1)
8.1.4 One of the turning points of ƒ is (−1;−9). Determine the coordinates of the other turning point of ƒ. (5)
8.1.5 On the ANSWER SHEET provided, sketch the graph of f. Clearly show all the coordinates of the turning points and intercepts with the axis. (4)
8.2 Determine the value(s) of a, if the average gradient of g(x) = 2x2 - x - 3 between x = a and x = 4 is 9. (5) [19]
QUESTION 9
The driver of a motor car fills the petrol tank of his car to full capacity in a petrol station, to undertake a journey that requires a minimum of 25 ℓ of fuel to drive.
Unfortunately, he knocks his car on the corner of the road pavement as he leaves the petrol station resulting into a leakage from an opening in his petrol tank.
The picture below shows the damaged petrol tank of the car.
The equation, V(t) = t2 - 9t + 35 represents the amount of petrol lost over time (t) in minutes.
Determine:
9.1 The amount of petrol in the tank before the leakage (2)
9.2 The amount of petrol that leaked out after 1 minute (2)
9.3 The time it took for maximum petrol to leak out of the tank (3)
9.4 The maximum amount of petrol that leaked (2) [9]
QUESTION 10
10.1 Determine the integral:![]()
10.2 The graph of ƒ and g defined by ƒ(x) = -x + 4 and g(x) = 2/x respectively, intersect at x = 0,59 and x = 3,41, as shown in the diagram below.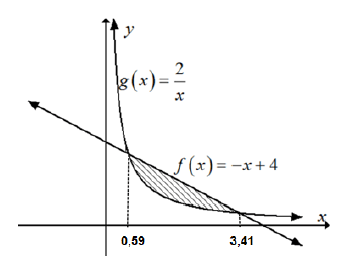
10.2.1 Determine the area bounded by the graph of ƒ(x) = -x + 4 and the x-axis, between x = 0,59 and x = 3,41. (6)
10.2.2 If it is given that the area bounded by the graph of g and the x-axis between x = 0,59 and x = 3,41 is equal to 3,51 square units, calculate the striped area between the graphs of ƒ and g. (3)
[13]
TOTAL: 150
INFORMATION SHEET: TECHNICAL MATHEMATICS


ANSWER SHEETS
NAME: ............................................................
SCHOOL: ............................................................
QUESTION 3.4

ANSWER SHEET
NAME:
SCHOOL:
QUESTION 8.1.5

Technical Sciences P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
MEMORANDUM
QUESTION 1
1.1 A(2)
1.2 A(2)
1.3 B(2)
1.4 C(2)
1.5 A (2)
1.6 B(2)
1.7 A(2)
1.8 C(2)
1.9 A(2)
1.10 B(2) [20]
QUESTION 2
2.1 A series of organic molecules that can be described by the same general formula and where each member differs from the next by a CH2 group. (2)
2.2 2.2.1 Organic molecules with the same molecular formula, but different structural formula. (2)
2.2.2 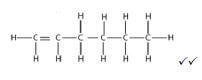 (2)
(2)
2.2.3 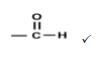 Aldehydes (2)
Aldehydes (2)
2.2.4 3-Chlorobut-1-ene (2)
2.2.5 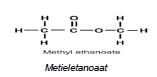
Methyl part | 1 mark |
|
Ethanoate part (functional group) | 1 mark |
|
(2)
2.3
2.3.1 Small organic molecules that can be covalently bonded to each other in a repeating pattern. (2)
2.3.2 2-Ethene (2)
2.3.3
- Manufacturing of plastic bags
- Synthesis of bullet proof vests
- Manufacturing of plastic bottles
- Manufacturing of cling wrap (Any 2) (2)[18]
QUESTION 3
3.1 CnH2n+2 (1)
3.2 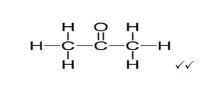 (2)
(2)
3.3 Propanal (2)
3.4
3.4.1 Hydrogen bonds and London forces (1)
3.4.2 Van der Waals forces (London forces) or Induced dipole force (Any one) (1)
3.5 As the strength of the intermolecular forces become stronger (increases) then the vapour pressure will become lower (decrease) OR As the strength of intermolecular forces become weaker, then the vapour pressure will become higher (increase). (2)
3.6 Ethanoic acid.
- Ethanoic acid has stronger intemolecular forces than Propan-1-ol hence a lower vapour pressure thus more energy will be required to overcome the intermolecular forces in ethanoic acid than in Propan-1-ol. The lower the vapour pressure, the higher the boiling point. (4) [13]
QUESTION 4
4.1 Addition (reaction) Hydation (1)
4.2
- Add sodium hydroxide or potassium hydroxide
- Heat the reaction mixture (2)
4.3 2-bromo butane (2)
4.4 
One mark for each reactant and product (3)
4.5 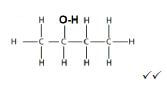
Butan-2-ol (3)
4.6 C4H8 + 6O2 → 4 CO2 + 4 H2O balance (3)
4.7 Hydrolysis (2) [16]
QUESTION 5
5.1
- An electrolyte is a substance of which the aqueous solution contains Ions.
OR
A substance that dissolves in water to give a solution that conducts electricity.
OR
A substance that forms free ions when melted. (2)
5.2 Temperature: 298 K or 25 °C
Concentration : 1 mol.dm-3 (2)
5.3
5.3.1 2 Cl- → Cl2 + 2e- (2)
5.3.2 Cu2+ + 2e- → Cu (2)
5.4 Electrolytic cell – Converts electrical energy to chemical energy. (2)
5.5 Q Reduction takes place (2)
5.6
5.6.1 Cu is a stronger reducing agent than Cl ions. Cu will be oxidised to Cu2+ ions resulting in the plate becoming eroded. (3)
5.6.2 Non-spontaneous (1) [16]
QUESTION 6
6.1 Galvanic Cell: Chemical energy is converted to electrical energy. (2)
6.2 External circuit or through the voltmeter. (2)
6.3 It maintains electrical neutrality OR It separates the two compartments so that they do not mix. (2)
6.4 Zn → Zn2+ + 2e- (2)
6.5 from Zn to Cu (1)
6.6 Zn + Cu2+ → Zn2+ + Cu (3)
6.7
- Eᶿcell = Eᶿcathode - Eᶿanode
= 0,34 – (-0,76)
= 1,1V (4)
6.8 It means they did not take the measurements at standard conditions where temperature is 298 K or 25 °C and concentration of 1 mol.dm-3. (3)
6.9
6.9.1 During solar construction, the following are identified as environmental threats:
- a release of greenhouse gases
- polution of drinking pure water (2)
6.9.2
- Lowers the electricity bill
- Increases home resale value
- Takes advantage of tax credits fom the goverment
- Net metering allows reselling of excess electricity to the utility company
(Any 2) (2) [23]
QUESTION 7
7.1 The incident ray, the reflected ray and the normal to the surface all lie in the same plane and the angle of reflection ᶿr = angle of incidence ᶿi. (2)
7.2
7.2.1 Total internal reflection (1)
7.2.2 Refraction (1)
7.3
- In the medical field
- In telecommunications
- In submarines (Any 2) (2)
7.4
- Light must travel from a more dense optical medium to a less dense optical medium
- The incident angle must be greater than the critical angle(2)
7.5
7.5.1 It is an angle of incidence in the denser medium such that the refracted rays just passes through the surface of separation of the two medium. (2)
7.5.2 24° (2)
7.6 A
- Because of the phenomenon of total internal reflection, the cut will glow brighter than that of B (2)
7.7
7.7.1 Dispersion is when white light spreads into its component colours. (2)
7.7.2 Violet (blue region ) (1)
7.7.3 It has a higher frequency. The higher the frequency, the less the degree of refraction. (2) [19]
QUESTION 8
8.1 Refraction is the bending of light when it passes from one optical medium to another. (2)
8.2
- Incident ray
- Refracted ray (2)
8.3
8.3.1 20° (1)
8.3.2 41° (2)
8.4
8.4.1
- Real Image
- Inverted
- Enlarged Image (3)
8.4.2
- Used in film projectors
- Used in microscopes
- Used in photographic zoom lens (Any 2) (2) [12]
QUESTION 9
9.1 It is a wave with a changing magnetic and electric field perpendicular to each other in the direction of propagation of the wave. (2)
9.2
- Lifting of heavy objects
- In music equipment (loudspeakers)
- In transmission of signals
- In communication systems
(Any 3) (3)
9.3 They have a penetrating ability into the skin that can cause skin cancer. (2)
9.4  (5)
(5)
9.5 SMALLER THAN (1) [13]
TOTAL: 150
Technical Sciences P2 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page in the ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- You may use a non-programmable calculator.
- Leave ONE line between two sub-questions for example between QUESTION 2.1 and QUESTION 2.2.
- You are advised to use the attached DATA SHEETS.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your final numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, et cetera where required. 10. Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question number (1.1–1.10) in the ANSWER BOOK, for example 1.11 E.
1.1 The organic compound below is an example of a …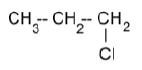
- primary haloalkane.
- secondary haloalkane.
- tertiary haloalkane.
- branched alkane. (2)
1.2 The IUPAC name of the following compound is …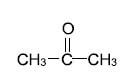
- propanone.
- propanal.
- propanoic acid.
- propanol. (2)
1.3 Ethene can be converted into other carbon-containing compounds using the reactants shown in the following flow chart.
Compounds X and Y are respectively:
X | Y | |
A | bromoethane | methanol |
B | bromoethane | ethanol |
C | bromoethene | ethanoic acid |
D | bromoethene | ethane hydroxide |
(2)
1.4 In which ONE of the following options are the three compounds listed in increasing order of vapour pressure?
- propanoic acid, pentane, butan-1-ol
- propanoic acid, butan-1-ol, pentane
- pentane, butan-1-ol, propanoic acid
- butan-1-ol, propanoic acid, pentane (2)
1.5 An electrochemical cell is to be set up to plate a nickel object with silver. Which ONE of the combinations below CORRECTLY shows the metal used for the positive electrode and the electrolytic solution in the electrochemical cell?
METAL USED FOR POSITIVE ELECTRODE | ELECTROLYTE SOLUTION | |
A | silver | silver nitrate |
B | silver | nickel sulphate |
C | nickel | silver nitrate |
D | nickel | nickel sulphate |
(2)
1.6 The cell notation for a standard Zn–Cu electrochemical cell is:
- Cu2+(aq) / Cu(s) // Zn(s) / Zn2+(aq)
- Zn(s) / Zn2+(aq) // Cu2+(aq) / Cu(s)
- Cu(s) / Zn2+(aq) // Cu2+(aq) / Zn(s)
- Zn(s) / Zn2+(aq) // Cu(s) / Cu2+(aq) (2)
1.7 Which ONE of the following properties demonstrates the wave nature of light?
- Light can be refracted
- Light travels at a speed of 3 x 108 m.s-1
- White light can be separated into a number of different colours
- Light is diffracted after passing through a narrow slit (2)
1.8 A ray of light strikes a rectangular Perspex block so that the angle between the ray and the side of the block is 40°, as shown in the
diagram.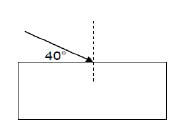
Which ONE of the statements below is correct?
- Angle of incidence is 50°
- Angle of refraction is 40°
- Angle of incidence is 40°
- Angle of refraction is 50° (2)
1.9 A ray of light falls obliquely on the centre of the straight edge of a semi circular glass slab. Which ONE of the following diagrams represents the path of the ray through the slab? 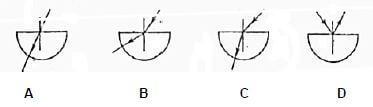 (2)
(2)
1.10 Optical fibres are used in telecommunication because light can be …
- externally reflected.
- internally reflected.
- externally refracted.
- internally refracted. (2) [20]
QUESTION 2 (Start on a NEW page.)
Organic chemistry is the chemistry of organic molecules divided into homologous series which are identified by the functional groups.
2.1 Define the term homologous series. (2)
2.2 Study the organic molecules listed below.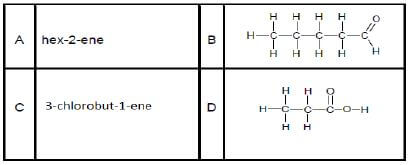
2.2.1 Define the term isomers in words. (2)
2.2.2 Draw the structural formula of a positional isomer of A. (2)
2.2.3 Write down the structural formula of the functional group of B and next to it write down the name of the homologous series to which B belongs. (2)
2.2.4 Draw the structural formula of compound C. (2)
2.2.5 Write down the structural formula of ONE functional isomer of compound D. (2)
2.3 The diagram below shows the structural formula for polyethylene. This is the industrial organic product used in the preparation of plastics.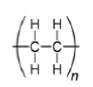
2.3.1 Describe the term monomer. (2)
2.3.2 Write down the IUPAC name of the monomer that formed polyethylene. (2)
2.3.4 Give TWO uses of polyethylene. (2) [18]
QUESTION 3 (Start on a NEW page.)
The table below shows the vapour pressures of various organic compounds at 25 °C.
Compound | Molar mass (g mol-1) | Vapour pressure (X 102 Pa) |
Pentane | 72 | 573,0 |
Hexane | 86 | 160,0 |
Heptane | 100 | 48,0 |
Propan -1-ol | 60 | 21,0 |
Propan -2 ol | 60 | 44,0 |
Butan -1 ol | 74 | 6,2 |
Butan -2 ol | 74 | 18,3 |
Pentan -1-ol | 88 | 2,2 |
Pentan -2- ol | 88 | 8,04 |
Ethanoic acid | 60 | 15,3 |
Propanone | 58 | 240,0 |
3.1 Write down the general formula of the homologous series to which heptane belongs. (1)
3.2 Draw the structural formula of propanone. (2)
3.3 Give the IUPAC name of an isomer of propanone. (2)
3.4 From the table above, write down the name of the intermolecular forces involved in the following:
3.4.1 Alcohols (1)
3.4.2 Alkanes (1)
3.5 State and explain the relationship between vapour pressure and the strength of intermolecular forces. (2)
3.6 Which compound will have the higher boiling point?
Ethanoic acid OR Propan-1-ol
Refer to intermolecular forces and energy in giving reasons for your answer to this difference. (4) [13]
QUESTION 4 (Start on a NEW page.)
The flow diagram below represents a series of organic reactions that took place.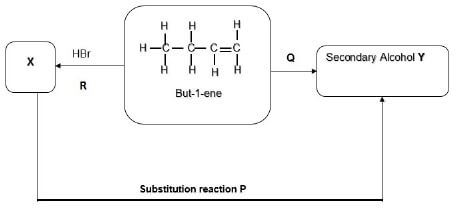
4.1 Name the type of organic reaction represented by reaction Q in the diagram. (1)
4.2 Give the reaction condition(s) required for reaction P which is the hydrohalogenation reaction that forms compound X to take place. (2)
4.3 Write down the IUPAC name of compound X. (2)
4.4 Using structural formulae, write down an equation that represents reaction R which is hydrohalogenation. (3)
4.5 Draw the structural formula of the product Y and give its IUPAC name. (3)
4.6 Write down a balanced equation for the complete combustion of butene (C4H8) in oxygen. (3)
4.7 Give the name of the substitution reaction represented as reaction P. (2) [16]
QUESTION 5 (Start on a NEW page.)
In the electrolytic cell, represented below, two CARBON RODS are used as electrodes and a concentrated copper (II) chloride solution is used as an electrolyte.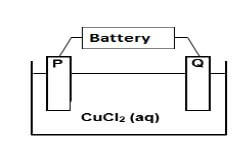
When the cell is functioning, a gas is released at electrode P, whilst electrode Q is coated with a reddish brown layer.
5.1 Define the term electrolyte. (2)
5.2 Give TWO standard conditions for the electrolytic cell when it is in operation. (2)
5.3 Write down a half-reaction to explain the observation made at:
5.3.1 Electrode P (2)
5.3.2 Electrode Q (2)
5.4 What energy conversion is taking place in this cell? (2)
5.5 Which electrode, P or Q, is the cathode? Give a reason for the answer. (2)
5.6 The carbon rods in the above cell are now replaced with COPPER RODS. The following observations are made at electrode P:
- No gas is released
- Its surface appears rough and eroded
5.6.1 Refer to the RELATIVE STRENGTHS OF REDUCING AGENTS to explain this observation. (3)
5.6.2 Will this electrolytic cell operation be a “spontaneous” or “non spontaneous” process? (1) [16]
QUESTION 6 (Start on a NEW page.)
The potential difference of a galvanic cell is measured experimentally by learners. Learners decided to further COMPARE the experimental as well as the calculated potential difference value.
They set up the galvanic cell shown below. 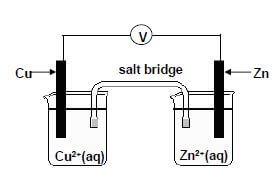
The voltmeter measures an initial reading of 0,9 V.
6.1 Write down the energy conversion that takes place in this cell. (2)
6.2 Which section of the cell will be responsible for electron flow when the cell is in operation? (2)
6.3 State ONE function of the salt bridge other than completing the circuit. (2)
6.4 Write down the half-reaction that takes place at the anode. (2)
6.5 In which direction will the electrons in the external circuit flow when this cell delivers a current? Write down only from Cu to Zn or from Zn to Cu. (1)
6.6 Write down the balanced net (overall) cell reaction. (3)
6.7 Use the Table of Standard Reduction Potential to calculate the initial potential difference (emf) of the above cell at STANDARD CONDITIONS. (4)
6.8 From the results obtained the learners conclude that the measured potential difference differs from the calculated potential difference. Give possible reasons for this difference in values. (3)
6.9 South Africa is experiencing an electricity crisis. There is an alarming shortage of coal which used to be a traditional source of electricity generation in the country. Eskom’s grid is on the law and hence the alternative forms of energy. There are noticeable wind farms in most parts of the country as a form of renewable energy. The most popular type of these forms of renewable energy is photo-voltaic which uses silicon cells that traps radiant energy from the sun hence they are commonly known as solar panels. Global warming is also another universal crisis that can be addressed by use of renewable energies as form of electricity.
6.9.1 Explain TWO environmental threats when solar panels are installed during the construction stage. (2)
6.9.2 What are the economic advantages of using solar panels? (2) [23]
QUESTION 7 (Start on a NEW page.)
‘A diamond is judged by four distinct factors that combine in a number of ways to arrive at its value.’ These are called the 4 C’s and are as follows:
- Carat weight
- Clarity
- Colour
- Cut
Of all the 4 C’s, cut is the one most directly influenced by man. The other three are dictated by nature. The cut or make of a diamond will dramatically influence its fire and sparkle, for it is the cutters skill that releases its beauty.” Geology 306 shows the ray path inside the diamond crystal.
Diagrams A and B below illustrate two different cuts of diamond and the way each cut handles light.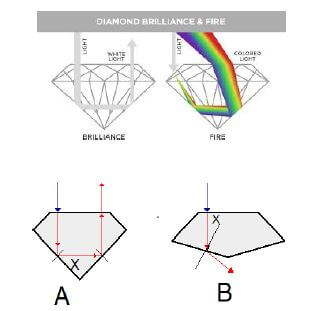
7.1 State the Law of Reflection. (2)
7.2 Identify the following:
7.2.1 Phenomenon illustrated in diagram A (1)
7.2.2 Phenomenon illustrated in diagram B (1)
7.3 Give TWO fundamental applications of the phenomenon illustrated in diagram A above. (2)
7.4 What TWO conditions must be satisfied in order for light to behave as it does in diagram A? (2)
7.5 The critical angle for diamond is 24°.
7.5.1 Define the term critical angle. (2)
7.5.2 Give a possible value for angle X in diagram B. Choose your answer from the values given below.
| 22° | 24° | 26° |
(2)
7.6 Mr I.A.M. Cheap is shopping for a diamond for his wife. Which cut (A or B) do you think his wife would prefer? Give a clear reason for your choice. (2)
7.7 In the diagram “Diamond Brilliance & Fire” above we noticed that white light is changing into the seven primary colours of the spectrum.
7.7.1 Define the phenomenon of these seven colours of the spectrum. (2)
7.7.2 Which colour is refracted the least in the spectrum? (1)
7.7.3 Explain your answer to QUESTION 7.7.2 above in terms of the frequency of light. (2) [19]
QUESTION 8 (Start on a NEW page.)
The diagram below shows the path of a ray of light through one corner of a cube of ice.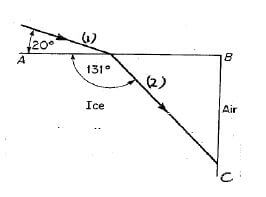
8.1 Define the term refraction. (2)
8.2 Give the names for the rays labelled 1 and 2 in the above diagram. (2)
8.3 Give the value of the following angles:
8.3.1 The angle of incidence on the face AB (1)
8.3.2 The angle of refraction on the face AB (2)
8.4 The diagram below shows an object placed between 2F and F from the lens.
Ray diagrams are used to determine the position and size of images formed.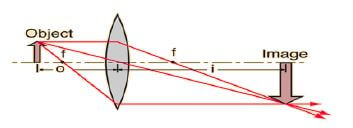
8.4.1 Give THREE characteristics of the image formed in the diagram. (3)
8.4.2 Name TWO practical uses of the above image formation. (2) [12]
QUESTION 9 (Start on a NEW page.)
The diagram below shows the different radiations of the electromagnetic spectrum. They are arranged according to their increasing frequencies.
9.1 Define an electromagnetic wave. (2)
9.2 Give THREE industrial applications of electromagnetic radiation. (3)
9.3 Why are ultraviolet rays considered to be harmful radiations? (2)
9.4 Calculate the energy of a photon of electromagnetic wave with a wavelength of 650 nm. (5)
9.5 Suppose an electromagnetic wave of wavelength 665 nm is available instead. How will the energy of this photon compare with that calculated in QUESTION 9.4? (Write only GREATER THAN, SMALLER THAN or EQUAL TO.) (1) [13]
TOTAL: 150
DATA TABLES FOR TECHNICAL SCIENCE GRADE 12
PAPER 2
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Standard pressure | pθ | 1,01 x 105 Pa |
Standard temperature | Tθ | 273 K |
Speed of light in a vacuum | c | 3,0 x 108 m·s-1 |
Planck's constant | h | 6,63 x 10-34 J·s |
TABLE 2: WAVES, SOUND AND LIGHT
TABLE 3: ELECTROCHEMISTRY
Eθcell = Eθcathode - Eθanode |
TABLE 4A: STANDARD REDUCTION POTENTIALS
TABLE 4B: STANDARD REDUCTION POTENTIALS
TABLE 3: THE PERIODIC TABLE OF ELEMENTS
Technical Sciences P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
MEMORANDUM
QUESTION 1
1.1 B (2)
1.2 B (2)
1.3 B (2)
1.4 B (2)
1.5 A (2)
1.6 A (2)
1.7 B (2)
1.8 B (2)
1.9 D (2)
1.10 B (2) [20]
QUESTION 2
2.1
2.1.1 When a net force acts on an object, the object accelerates in the direction of the force. This acceleration is directly proportional to the net force and inversely proportional to the mass of the object. (2)
2.1.2
- Normal
- Force of gravity
- Tension (3)
2.1.3
- Fnet = ma
T = (10)(0,3)
T = 3 N (3)
2.1.4 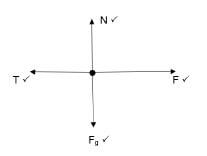 (4)
(4)
2.1.5
- Fnet = ma
F – T = ma
F – 3 = (20)(0,3)
F = 9 N (4)
2.1.6 Increases (1)
2.1.7 Increases (1)
2.2
2.2.1
- Pair 1 – Force exerted by the ring on the wall
Force exerted by the wall on the ring. - Pair 2 – Force exerted by the spring balance A on B
Force exerted by the spring balance B on A - Pair 3 – Force applied by learner on spring balance A
Force exerted by the spring balance A on the learner
(Any TWO sets)(Per set )(4)
2.2.2 3 N (2)
2.2.3
- Newton’s third law/Newton se derde wet.
When object A exerts a force on object B, object B simultaneously
exerts an oppositely directed force of equal magnitude on object A. (3) [27]
QUESTION 3
3.1
3.1.1 Impulse is defined as the product of the net force acting on an object and the time (the net force acts on the object.)(2)
3.1.2 (4)
| OPTION 1 Upward POSITIVE FnetΔt = Δp Fnet(0,01) = [0,06)(8 – (−14)] Fnet = 132 N | OPTION 2 Downward POSITIVE FnetΔt = Δp Fnet(0,01) = [0,06)(−8 – (14)] Fnet = −132 N Fnet = 132 N |
3.1.3 132 N (1)
3.1.4 Decreases (1)
3.2
- Air bags
- Crumple zones
- Arrestor beds (3)
3.3 3.3.1 An isolated system is one on which the net external force acting on the system is zero. (2)
3.3.2
- Σpi = pi(car) + pi(truck)
= 5 000 + 0
= 5 000 kg.m.s-1 (2)
3.3.3 5 000 kg.m.s-1 (1)
3.3.4 The total linear momentum of an isolated system remains constant (is conserved). (2)
3.3.5
- Σpi = Σpf
5000 = pfcar) + pf(truck)
5000 = (−500) + (1500)vf
vf = 3,67 m.s-1 due East (3)
3.3.6
- ΣEki = ½ mcvic 2 + ½ mTviT 2 mcvic = 5000 vic = 5 m.s-1
= ½(1 000)(5)2 + 0
= 12 500 J
ΣEkf = ½ mcvfc 2 + ½ mTvfT 2 mcvfc = −500 vfc = − 0,5 m.s-1
=½(1 000)(−0,5)2 + ½(1 500)(3,67)2
=10 226,68 J
ΣEki ≠ ΣEkf
∴ Collision is inelastic / (7) [28]
QUESTION 4
4.1
4.1.1 The sum of potential energy and kinetic energy. (2)
4.1.2 B (1)
4.1.3 In an isolated system the total mechanical energy remains constant. (2)
4.1.4
- Mechanical energy at A = EP + EK
= 60 + ½mv2
= 60 + ½(0,2)(1,5)2
= 60,23 J
ME at/by A = ME at/by B
60,23 = mgh + ½mv2
60,23 = (0,2)(9,8)(4,5) + ½(0,2)v2
v2 = 514,05
v = 22,67 m.s-1 (6)
4.2
4.2.1
- F3 (1)
- Fgirl (1)
4.2.2(4)
| OPTION 1 Wnet = FnetΔx cosθ Wnet = (42 – 1,2)(3) cos 0° Wnet = 122,4 J |
| OPTION 2 Wnet = Wgirl + WF3 Wnet = Fgirl Δx cos θ + F3 Δx cosθ Wnet = (42)(3) cos 0° + (1,2)(3)(cos180°) Wnet = 122,4 J |
4.2.3 Power (1)
4.2.4
- Power = 400 W
Work done per second = 400 W
∴ Time taken = 1 s (2) [20]
QUESTION 5
5.1
5.1.1 A perfectly plastic body is a body which does not show a tendency to regain its original shape and size when the deforming force is removed. (2)
5.1.2 Modulus of elasticity / K (1)
5.1.3 B (1)
5.1.4 A (1)
5.1.5 C (1)
5.2
5.2.1 Pascal’s law states that in a continuous liquid at equilibrium, the pressure applied at a point is transmitted equally to the other parts of the liquid. (2)
5.2.2
- Area/Oppervlakte = πr2
= π (13 x10-2)2
= 0,053 m2
F1= F2
A1 A2
300 = 18 000
0,053 A2
A2 = 3,18 m2 (6) [14]
QUESTION 6
6.1 Capacitor is a device for storing electrical charge for a short time. (2)
6.2
- Filter circuits in power supplies.
- Separation of frequencies between the woofer (base) speaker.
- Power factor correction/improvement in electrical transmission systems. (ANY TWO )(2)
6.3
- Q = CV
Q = (10 x 10-6)(5)
Q = 50 x 10-6 C (3)
6.4
6.4.1 A semi-conductor is a material that has electrical conductivity between that of a conductor and an insulator. (2)
6.4.2 Silicon and Germanium (2)
6.4.3 p-type (2) [13]
QUESTION 7
7.1 The potential difference across a conductor is directly proportional to the current in the conductor at constant temperature. (2)
7.2 1
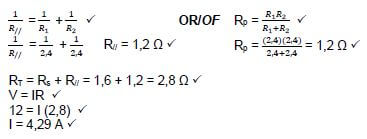 (6)
(6)
7.3
7.3.1 Decreases (1)
7.3.2 Current decreases RT increases when S1 is open (2) [11]
QUESTION 8
8.1
8.1.1 Faraday's law states that when the magnetic flux linked with the coil changes, an emf is induced in the coil. The magnitude of induced emf is directly proportional to the rate of change of magnetic flux. (2)
8.1.2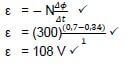 (3)
(3)
8.2
8.2.1
- A transformer that increases the voltage is called a step-up transformer.
A transformer that decreases the voltage is called a step-down transformer. (4)
8.2.2 Step-up transformer/Verhogingstransformator (2) [11]
QUESTION 9
9.1 DC generator. It has split ring commutator. (2)
9.2 Mechanical energy to electrical energy. (2)
9.3 Rectangular coil (1)
9.4 Principle of electromagnetic induction. (1) [6]
TOTAL: 150
Technical Sciences P1 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- Write your FULL NAME and SURNAME in the appropriate spaces on the ANSWER SHEET.
- Answer ALL the questions.
- Start each question on a NEW page in the ANSWER BOOK.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Number the answers correctly according to the numbering system used in this question paper.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions et cetera where required.
- You are advised to use the attached DATA SHEETS.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1–1.10.) in the ANSWER BOOK, for example 1.12 A.
1.1 The Law which states that an object will remain in its state of rest or continue moving with constant velocity unless it is acted upon by an unbalanced force is called …
- Lenz’s law.
- Newton’s first law.
- Newton’s second law
- Newton’s third law. (2)
1.2 An object of mass ‘m’ rests on a rough horizontal surface. A force F is applied causing the object to accelerate with magnitude ‘a’ as shown in the figure.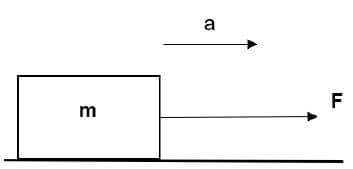
Which ONE of the following changes can be made to decrease the acceleration?
- Increase the magnitude of the applied force.
- Decrease the magnitude of the applied force.
- Decrease the mass of the object.
- Place the object on a smooth surface. (2)
1.3 An object’s velocity increases from v to 2v by applying a force.
The object’s momentum will be …
- halved.
- doubled.
- tripled.
- increased four times. (2)
1.4 Two identical trolleys are held together with a compressed spring as shown in the figure.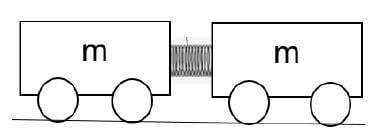
Which ONE of the following statements is TRUE about the magnitude of the momentum and velocity of the trolleys after the spring is released?
- Momentum and velocities of both trolleys are different.
- Momentum and velocities of both trolleys are the same.
- Both trolleys have the same velocity but different momentum.
- Both trolleys have the same momentum but different velocities. (2)
1.5 A constant force F of 50 N acts at an angle 30° with the horizontal and displaces a box by 8 m over a rough horizontal surface where the force of friction is 7 N.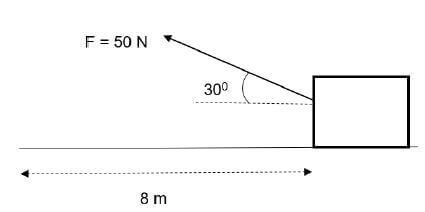
The work done, in Joule, by the vertical component of force F on the box is …
- 0.
- 200.
- 346,4.
- 400. (2)
1.6 In an experiment learners investigate the effect of depth on the pressure of a liquid. The learners allow water to spray out of holes (A, B, C and D) of equal diameter opened along the sides of a container as shown below.
One of the holes sprays out water the furthest, to point P.
From which hole will the water reach the furthest point P?  (2)
(2)
1.7 The maximum force that can be applied to a body so that the body regains its original form completely on removal of the force is called …
- stress.
- elastic limit.
- reforming force.
- deforming force. (2)
1.8 Which ONE of the following factors DOES NOT affect the capacitance of a capacitor?
- Area of the plates
- Time of flow of charge
- Distance between the plates
- Dielectric material used between the plates (2)
1.9 The process of producing electricity from motion is called …
- doping.
- etching.
- electrolysis.
- electromagnetic induction. (2)
1.10 A device that converts electrical energy to mechanical energy is a(n) …
- transistor.
- electric motor.
- electric heater.
- electric generator. (2) [20]
QUESTION 2
2.1 Two trolleys, A and B, are connected by a light string as shown in the diagram below. Force F is applied on trolley A and the trolley system accelerates at 0,3 m.s-2. The mass of trolley A is 20 kg and trolley B is 10 kg.
The trolleys are pulled over a frictionless surface.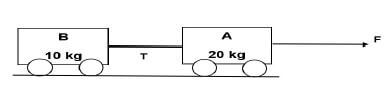
2.1.1 State Newton’s second law in words. (2)
2.1.2 Name all the forces acting on trolley B. (3)
2.1.3 Calculate the tension T on the string. (3)
2.1.4 Draw a free body diagram of all the forces acting on trolley A. (4)
2.1.5 Calculate the magnitude of force F. (4)
2.1.6 How would the tension T on the string change if the applied force F is increased? Write only INCREASE, DECREASE or REMAINS THE SAME. (1)
2.1.7 How would the acceleration of trolley A change if trolley B is detached by breaking the string while keeping the applied force F constant? Write only INCREASE, DECREASE or REMAINS THE SAME. (1)
2.2 The ring of spring balance B is fixed on a wall and spring balance A is attached to the hook of spring balance B. The ring of spring balance A is pulled to the left and it shows a reading of 3 N.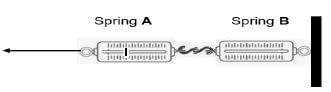
2.2.1 Write down any TWO sets of action-reaction pairs that act in the horizontal plane in the diagram. (4)
2.2.2 What is the reading on spring balance B? (2)
2.2.3 Name and state in words the law used to answer QUESTION 2.2.2. (3) [27]
QUESTION 3
3.1 A rigid ball of mass, 60 g, is dropped from a certain height above the ground. The ball strikes the ground with a velocity of 14 m.s-1.
The ball is in contact with the ground for 0,01 s and rebounds vertically up with a velocity of 8 m.s-1.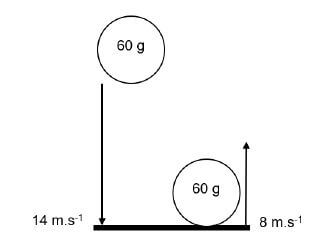
3.1.1 Define the term impulse. (2)
3.1.2 Calculate the magnitude of the force exerted by the ball on the ground. (4)
3.1.3 Write down the magnitude of the force exerted by the ground on the ball. (1)
3.1.4 The contact time is increased by replacing the rigid ball with a soft ball for the same change in momentum. How would the magnitude of the force exerted by the soft ball on the ground compare to the magnitude of the force exerted by the rigid ball? Write down only HIGHER, LOWER or REMAINS THE SAME. (1)
3.2 Give THREE applications of impulse in the context of road safety. (3)
3.3 A car of mass 1 000 kg is moving due east with a momentum of 5000 kg.m.s-1 collides with a stationary truck of mass 1 500 kg.
After the collision the car moves west with a momentum of 500 kg.m.s-1.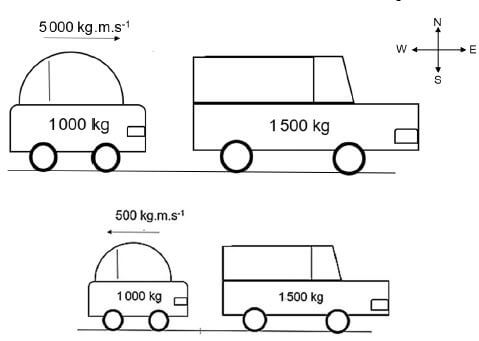
Consider the system as isolated.
3.3.1 Define the term isolated system. (2)
3.3.2 Calculate the magnitude of total momentum before the collision. (2)
3.3.3 What is the magnitude of the total momentum after the collision? (1)
3.3.4 State the principle of conservation of momentum in words. (2)
3.3.5 Calculate the velocity of the truck after the collision. (3)
3.3.6 Determine, by using a calculation, whether this collision is elastic or inelastic. (7) [28]
QUESTION 4
4.1 A block of mass 0,2 kg slides down a frictionless surface past point A at a speed of 1,5 m.s-1. The gravitational potential energy of the block at point A is 60 J. The block reaches point C, which is 4,5 m above the ground.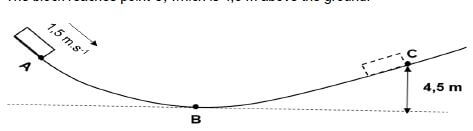
4.1.1 Define mechanical energy. (2)
4.1.2 At which point on the path of the block is its speed the greatest? Write down only A, B or C. (1)
4.1.3 State the principle of conservation of mechanical energy in words. (2)
4.1.4 Calculate the speed of the block at point B. (6)
4.2 The diagram given below shows the force diagram of all the forces acting on a box that is pulled by a girl with a force, Fgirl, of 42 N. The box moves 3 m horizontally to the right across a rough surface. The magnitude of force F3 is equal to 1,8 N.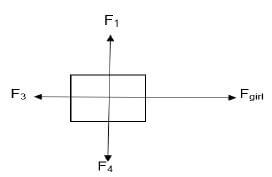
4.2.1 Identify the force that does:
- Negative work on the block (1)
- Positive work on the block (1)
4.2.2 Calculate the net work done on the block. (4)
The rate at which work is done by the girl to move the block 3 m is 400 W.
4.2.3 Give a term for the underlined phrase. (1)
4.2.4 Without using a calculation, how long does the block take to move 3 m? (2) [20]
QUESTION 5
Learners perform an investigation into the relationship between stress and strain and obtain the following graph.
Graph of Stress vs Strain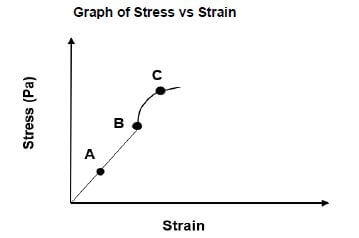
5.1
5.1.1 Define a perfectly plastic body. (2)
5.1.2 What does the gradient of the graph represent? (1)
5.1.3 At which point (A, B or C) is the elastic limit reached? (1)
Which point (A, B or C) lies in the:
5.1.4 Elastic region? (1)
5.1.5 Plastic region? (1)
5.2 The diagram shown below shows a hydraulic lift used to lift cars. A force of 300 N is exerted on a small circular piston of radius 13 cm to lift a car placed on a large piston as shown in the diagram below. Pressure is transmitted through a hydraulic fluid to the large piston.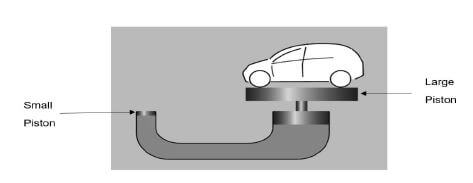
5.2.1 State Pascal’s law in words. (2)
5.2.2 Calculate the area of the large circular piston, if a minimum force of 18 000 N is required to lift the car. (6) [14]
QUESTION 6
6.1 What is the function of a capacitor? (2)
6.2 Give any TWO uses of a capacitor in technology. (2)
6.3 A battery of emf 5 V is connected to the parallel plates of a capacitor with capacitance 10 µF. Calculate the charge stored on the plates. (3)
6.4 An intrinsic semi-conductor is doped with an impurity element boron.
6.4.1 What is a semi-conductor? (2)
6.4.2 Give TWO examples of semi-conductors. (2)
6.4.3 What type (n-type or p-type) of semi-conductor is produced in the above process? (2) [13]
QUESTION 7
In the circuit diagram below the battery has an emf of 12 V. Lamps are connected as shown and Lamp 2 and Lamp 3 are identical.
The resistance of the connecting wires and battery may be ignored.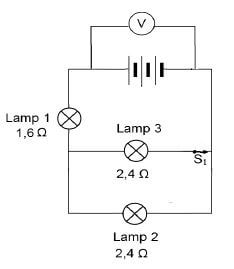
7.1. State Ohm’s law in words. (2)
7.2. Calculate the current that flows through Lamp 1. (6)
7.3 Switch S1 is now open.
7.3.1 How will the current in the circuit be affected by this change? Write only INCREASES, DECREASES, or REMAINS THE SAME. (1)
7.3.2 Explain your answer in QUESTION 7.3.1. above. (2) [11]
QUESTION 8
8.1 A solenoid with 300 turns is subjected to a varying magnetic field that changes the magnetic flux uniformly from 0,34 Wb to 0,7 Wb in an interval of 1 s.
8.1.1 State Faraday’s law of electromagnetic induction in words. (2)
8.1.2 Calculate the magnitude of the induced emf. (3)
8.2 An electrician wants to convert a potential difference of 120 V AC. to 240 V AC.
8.2.1 Differentiate between step-up and step-down transformers. (4)
8.2.2 What type of transformer must be used by the electrician? (2) [11]
QUESTION 9
A simple generator consists of a coil turning in a magnetic field which is produced by permanent magnets as shown in the diagram.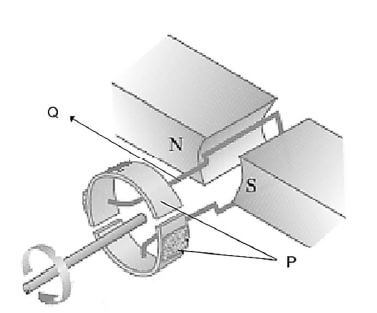
9.1 What type of generator is shown in the diagram? Give a reason for your answer. (2)
9.2 What energy change take place in the generator while it is in operation? (2)
9.3 Name component Q. (1)
9.4 On which principle or law is the working of the generator based? (1) [6]
TOTAL: 150
DATA FOR TECHNICAL SCIENCES GRADE 12
PAPER 1
TABLE 1: PHYSICAL CONSTANTS
| NAME | SYMBOL | VALUE |
| Acceleration due to gravity | g | 9,8 m·s-2 |
| Coulomb's constant | k | 9,0 x 109 N·m2·C-2 |
| Permittivity of free space | ε0 | 8,85 x 10-12 F.m-1 |
TABLE 2: FORMULAE
FORCE
WORK, ENERGY AND POWER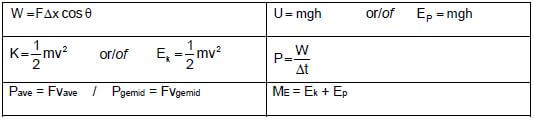
ELASTICITY, VISCOSITY AND HYDRAULICS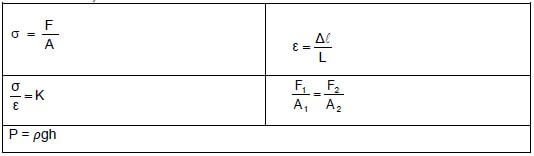
ELECTROSTATICS
CURRENT ELECTRICITY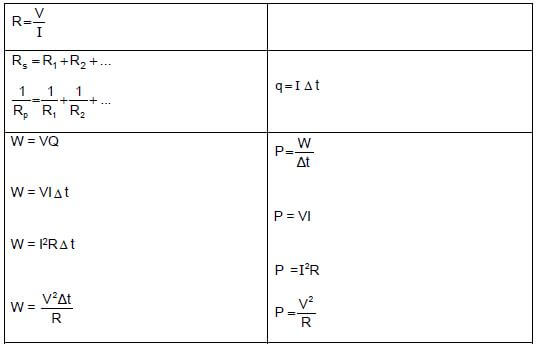
ELECTROMAGNETISM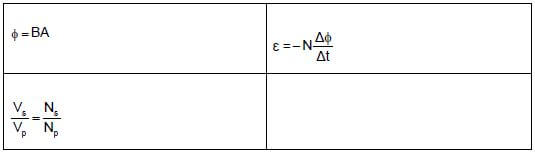
Engineering Graphics and Design P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
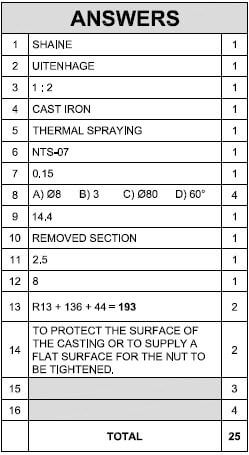
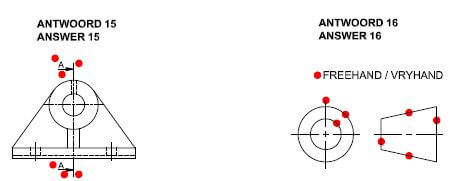
MEMORANDUM
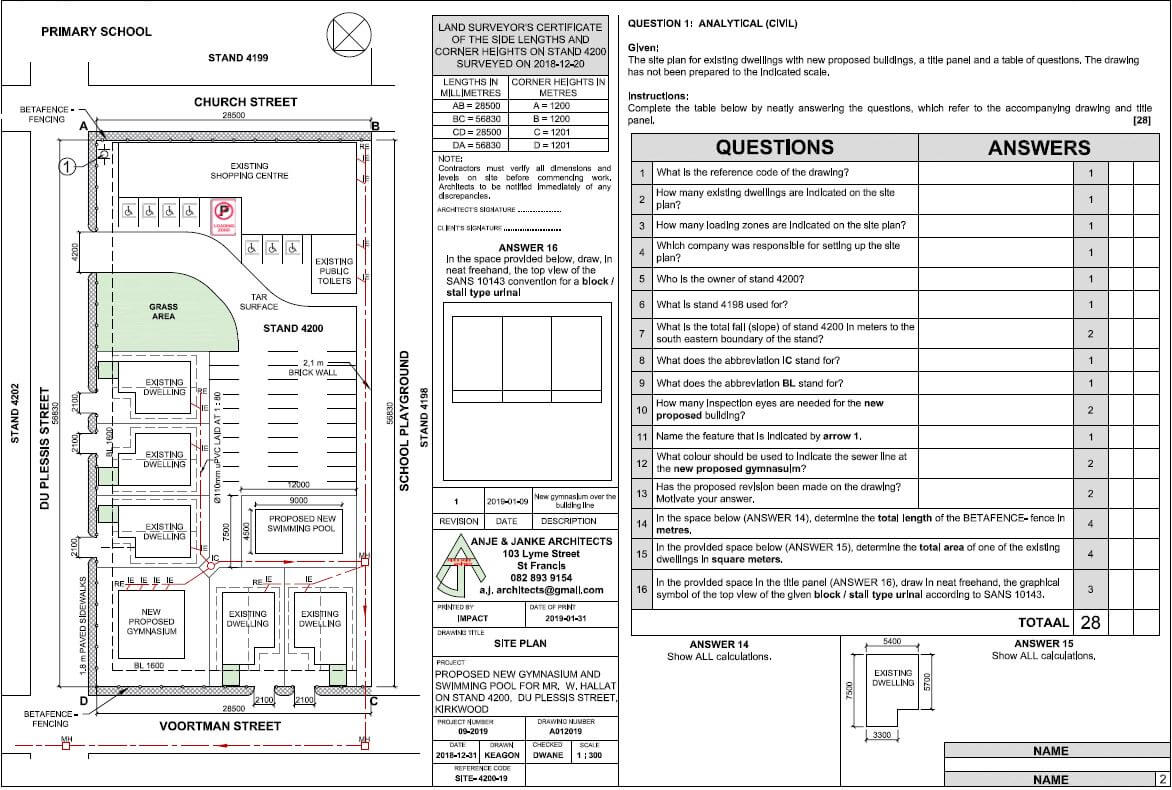
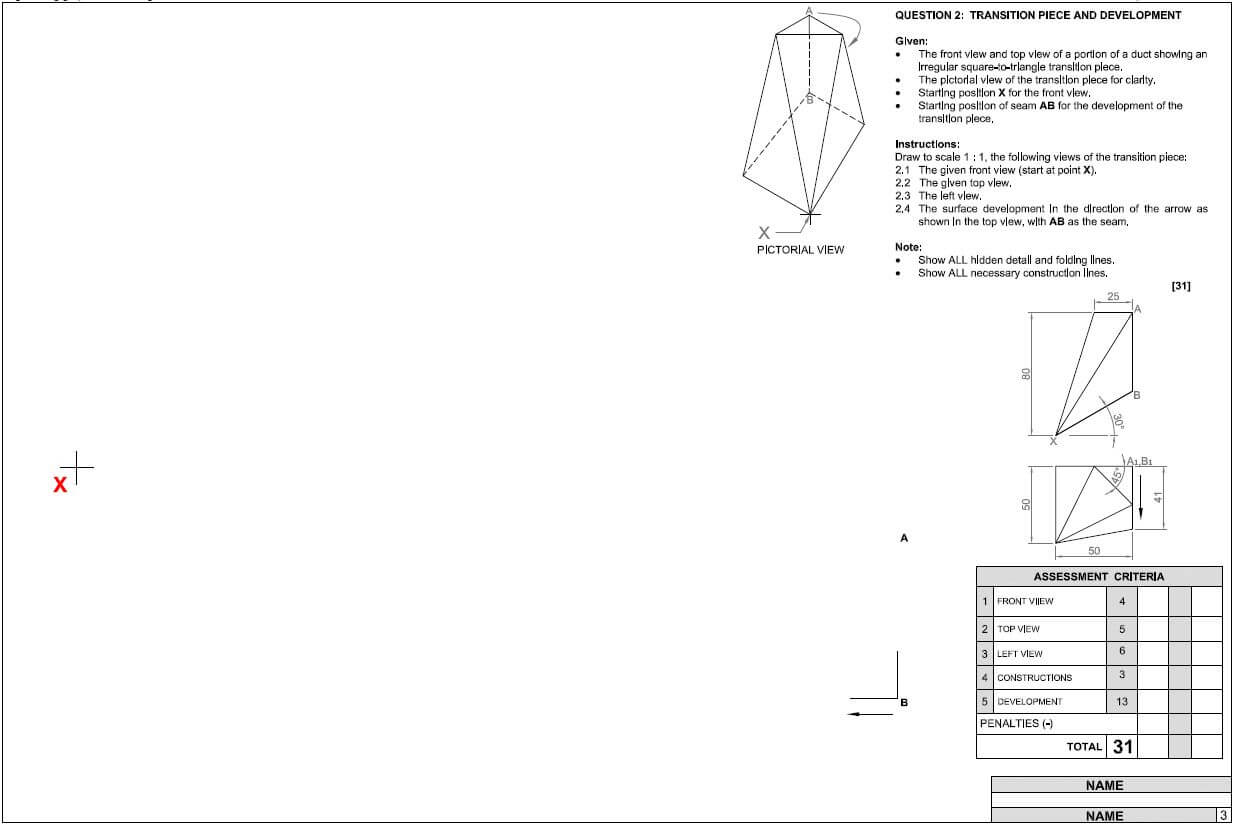
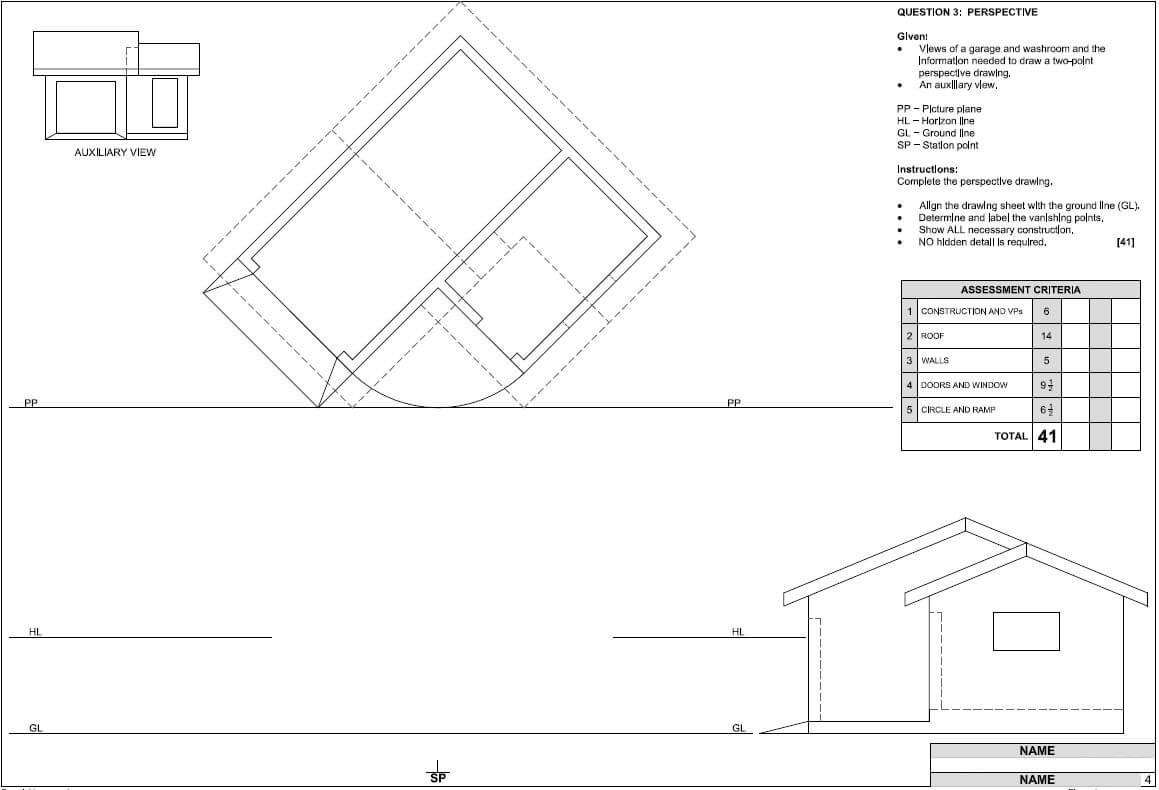
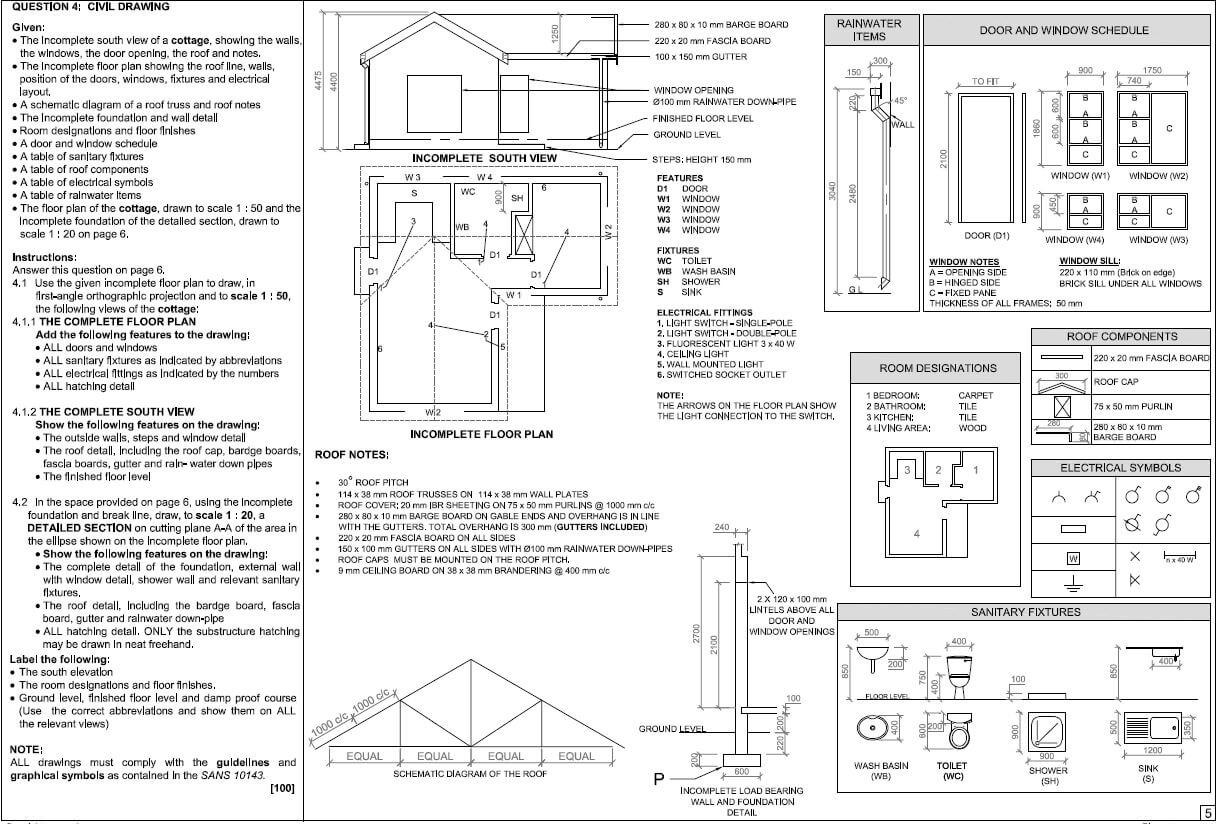
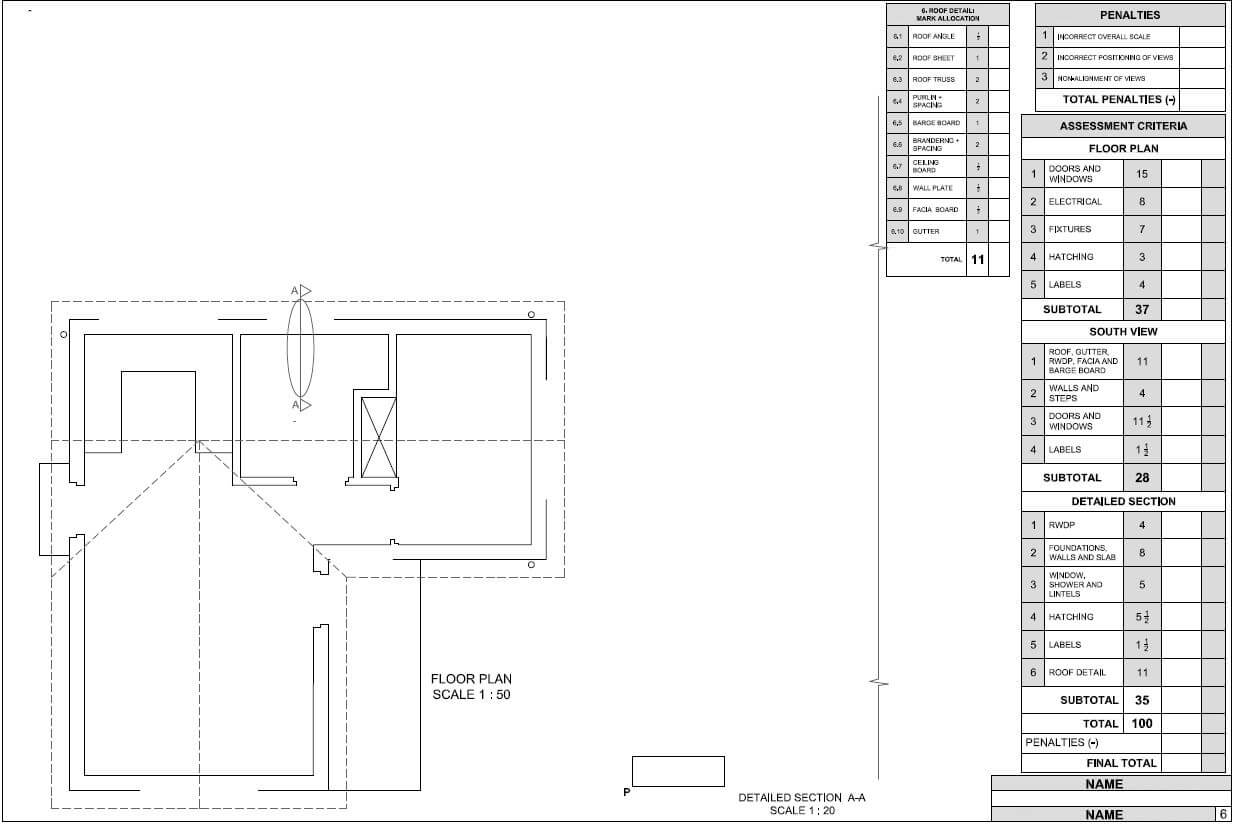
Engineering Graphics and Design P1 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
QUESTIONS

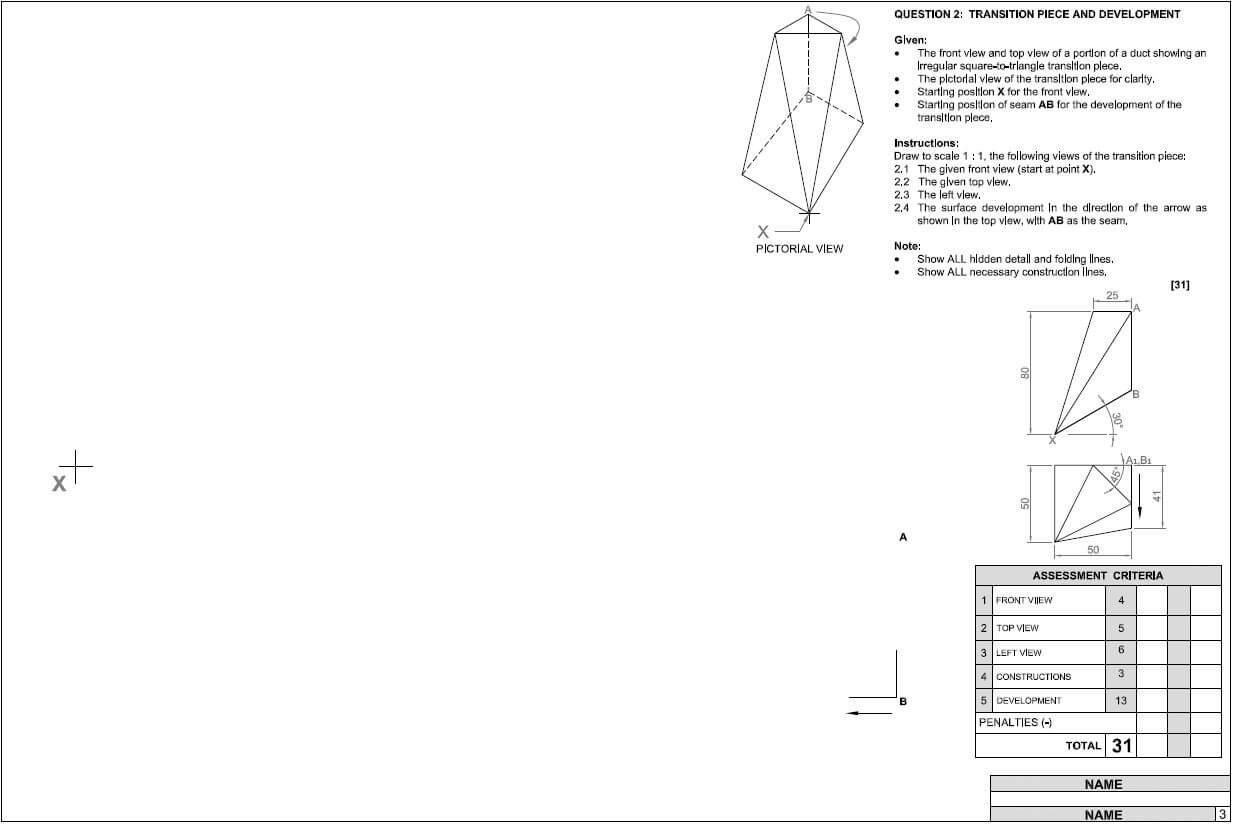
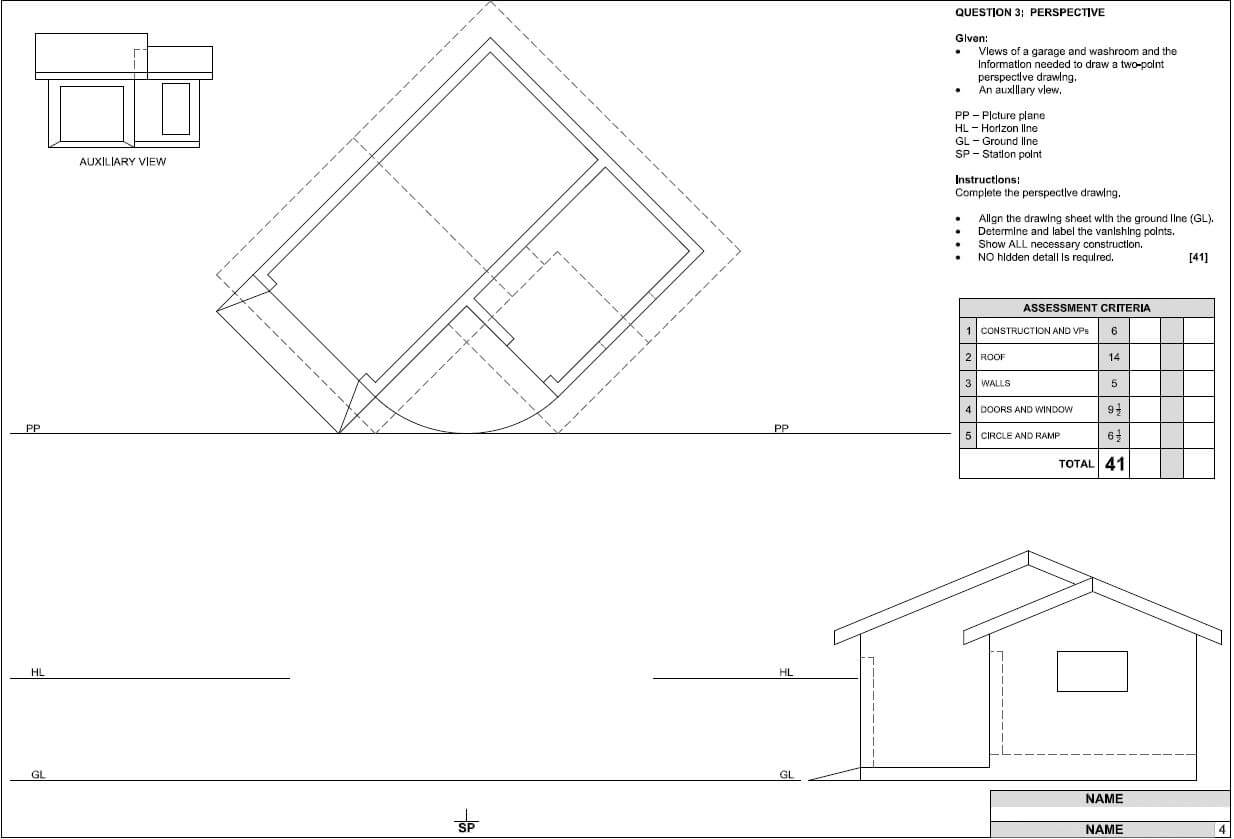
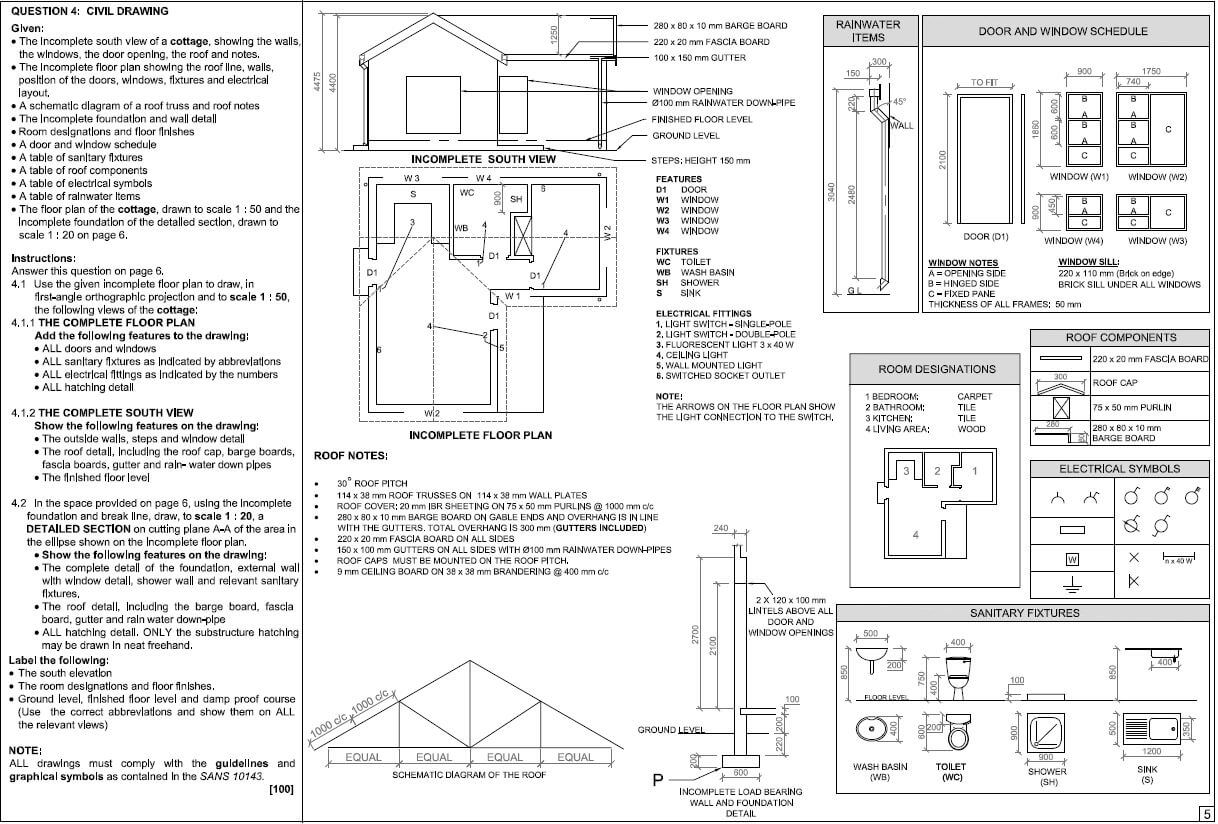
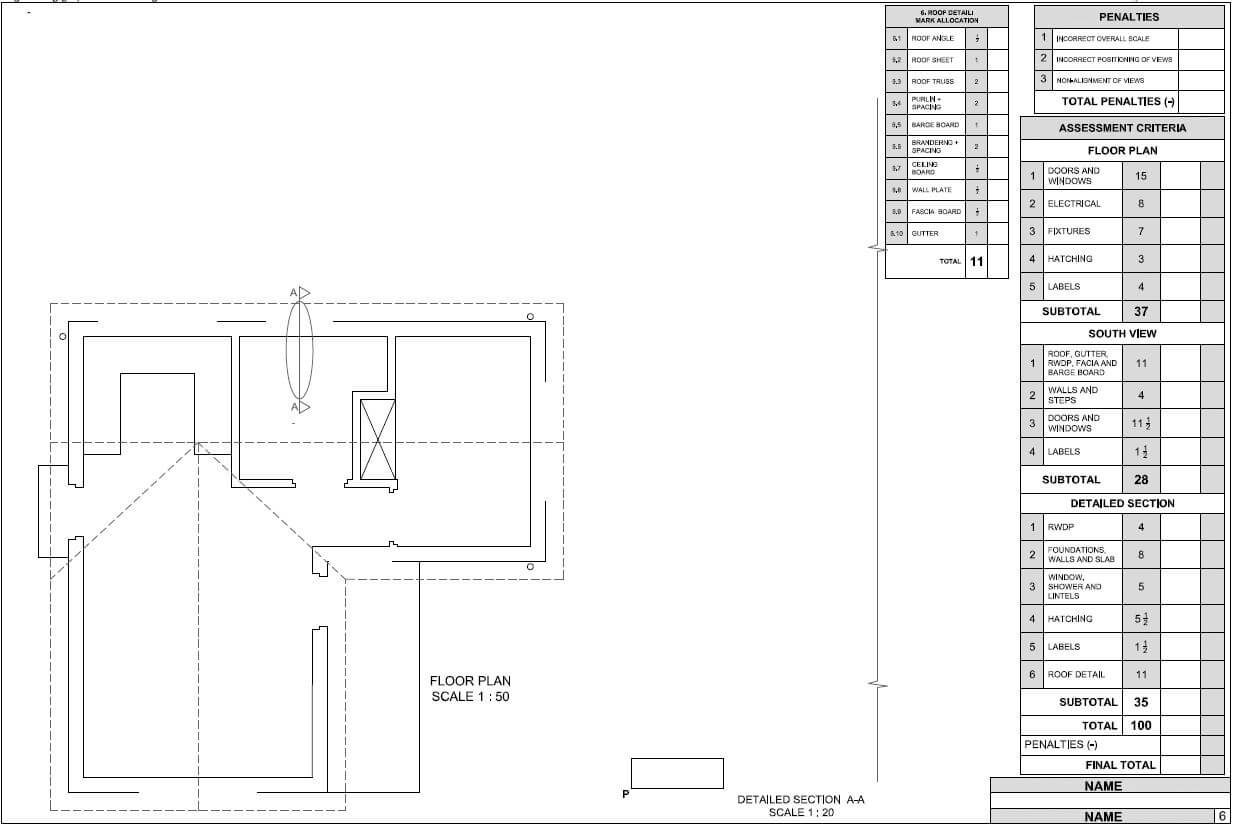
Engineering Graphics and Design P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
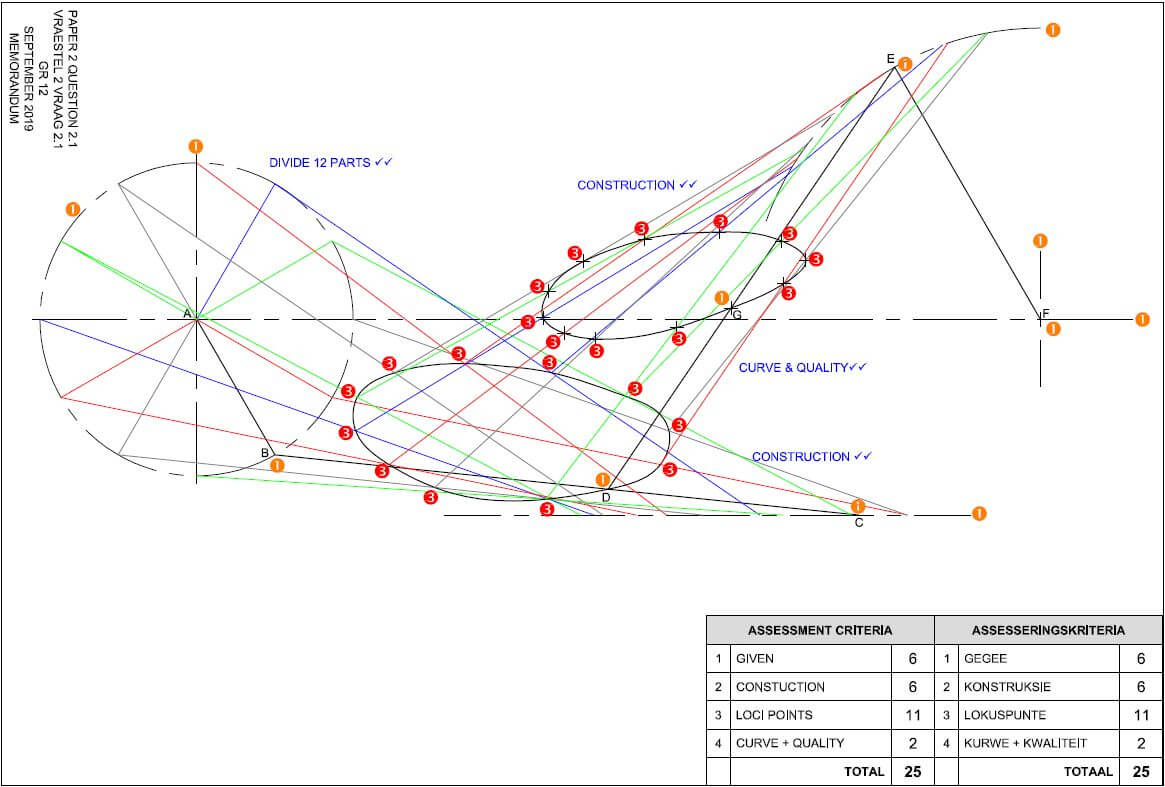
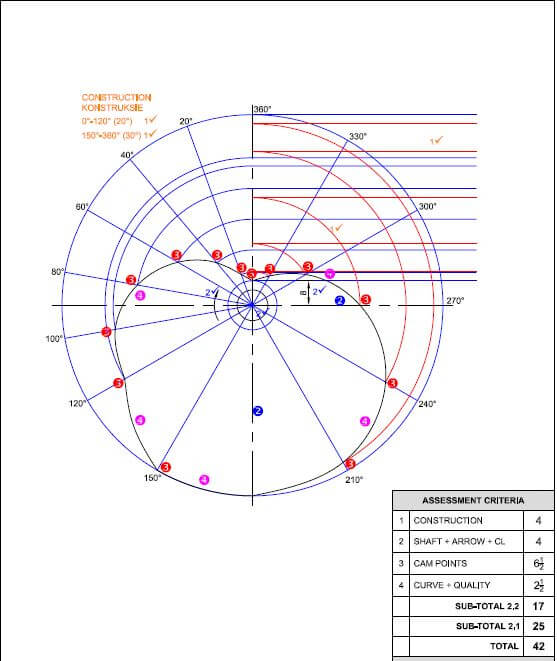
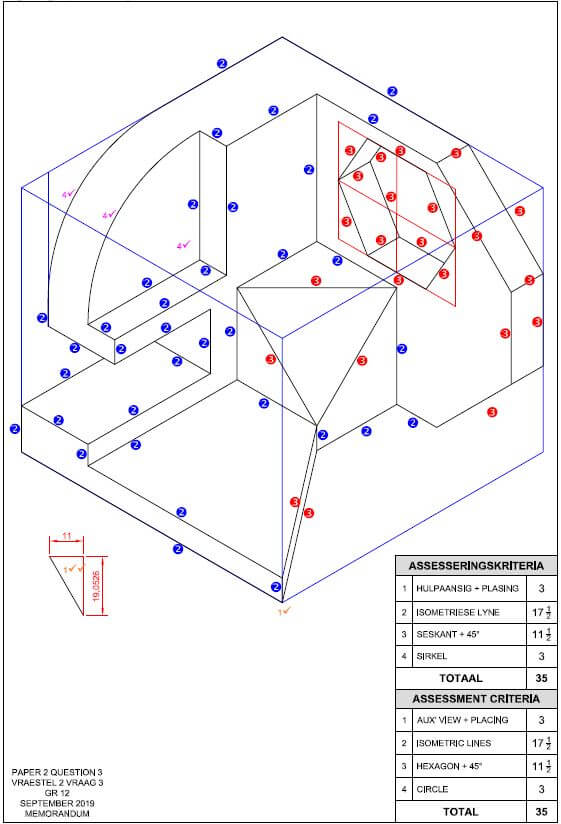
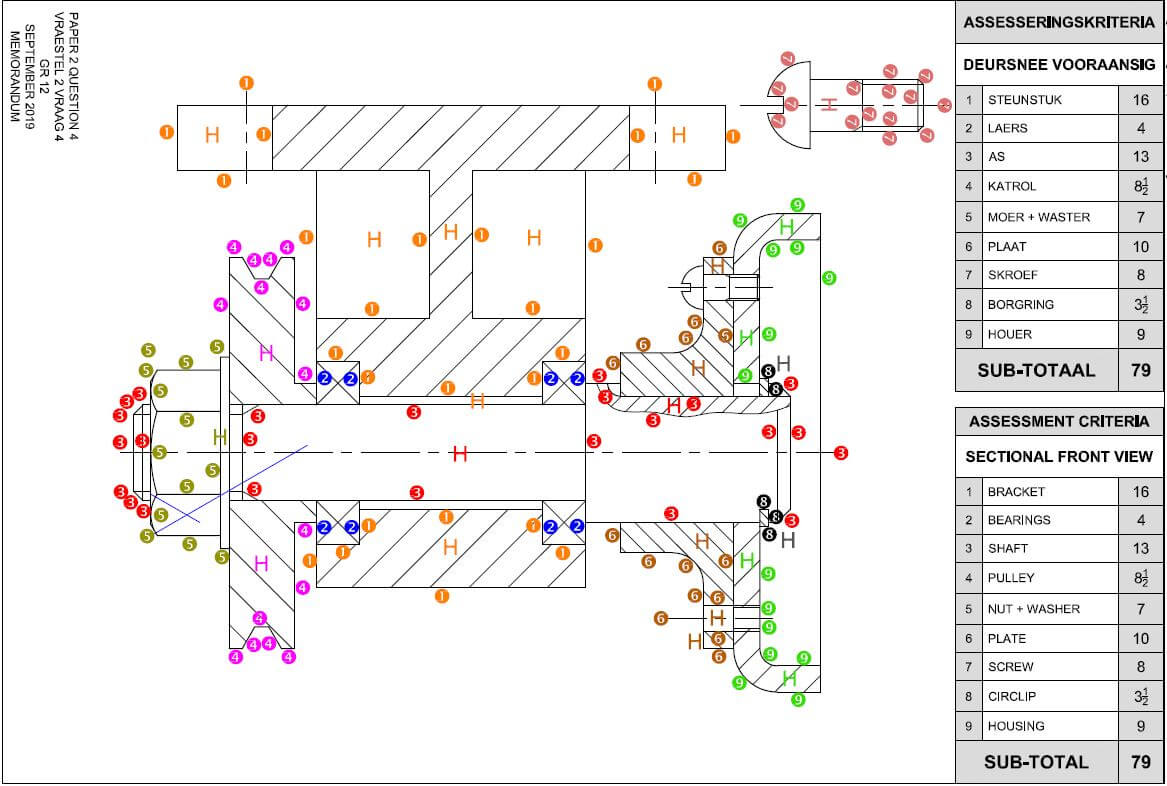
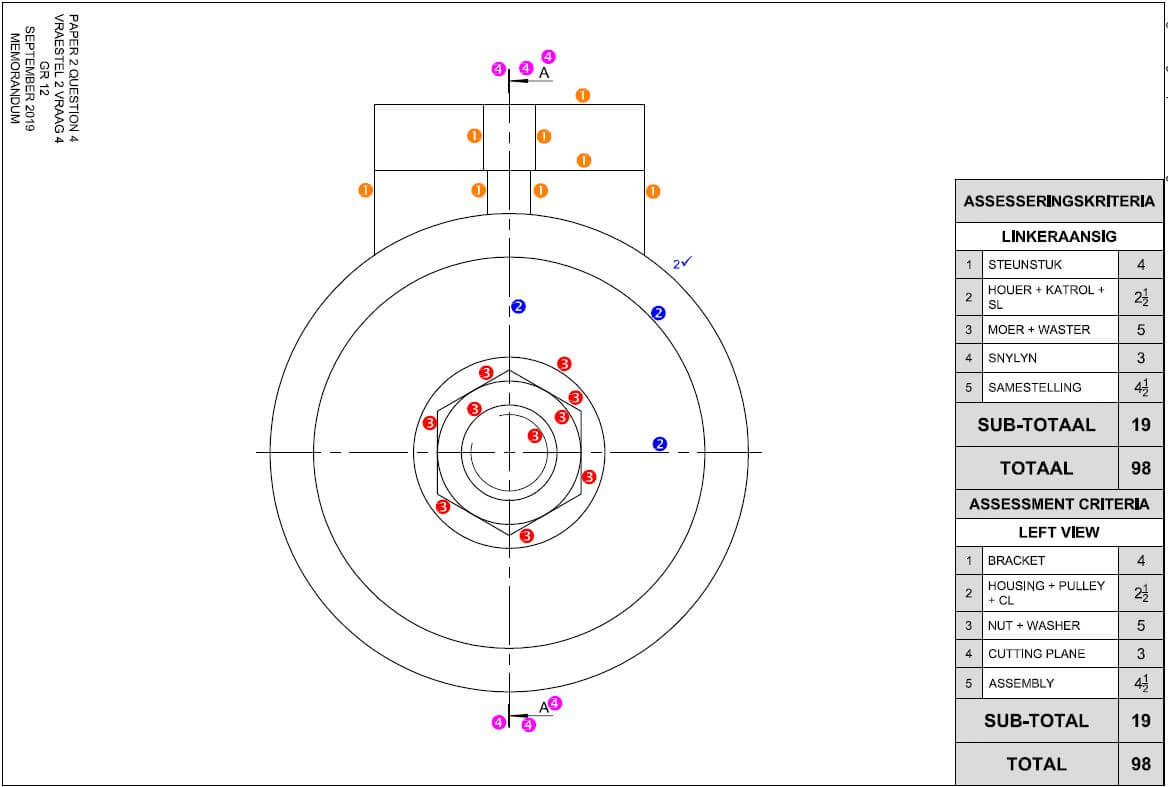
MEMORANDUM