Adele
MATHEMATICS PAPER 1 GRADE 12 QUESTIONS - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICS
PAPER 1
GRADE 12
AMENDED SENIOR CERTIFICATE
EXAMS PAST PAPERS AND MEMOS
MAY/JUNE 2018
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 (3x —1)(x + 4) = 0 (2)
1.1.2 2x2 + 9x —14 = 0 (correct to TWO decimal places) (4)
1.1.3 26x =3x (4)
1.1.4 (x-1)(x-4) > x+11 (5)
1.2 Simplify fully: √16x7 - √25x7
√x
1.3 Solve simultaneously for x and y: xy = 9 and x - 2y - 3 = 0 (5)
1.4 Prove that x2 + 2xy + 2y2 cannot be negative for x, y∈R. (4) [27]
QUESTION 2
2.1 Given the quadratic pattern: 5 ; 10 ; 17 ; 26 ; ....
2.1.1 Write down the next TWO terms of the pattern. (2)
2.1.2 Determine the formula for the nth term of the pattern. (4)
2.1.3 Which term of the pattern will have a value of 1 765? (4)
2.2 The first 24 terms of an arithmetic series are: 35 + 42 + 49 + ...... + 196. Calculate the sum of ALL natural numbers from 35 to 196 that are NOT divisible by 7. (5) [15]
QUESTION 3
Themba is planning a bicycle trip from Cape Town to Pretoria. The total distance covered during the trip will be 1 500 km. He plans to travel 100 km on the first day. For every following day he plans to cover 94% of the distance he covered the previous day.
3.1 What distance will he cover on day 3 of the trip? (2)
3.2 On what day of the trip will Themba pass the halfway point? (4)
3.3 Themba must cover a certain percentage of the previous day's distance to ensure that he will eventually reach Pretoria. Calculate ALL possible value(s) of this percentage. (3) [9]
QUESTION 4
The graph of f (x) = log4 x is drawn below. B (—6;p is a point on f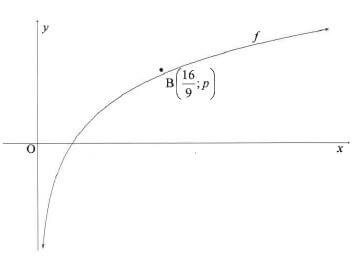
4.1 For which value(s) of x is log 4/3 x ≤ 0? (2)
4.2 Determine the value of p, without the use of a calculator. (3)
4.3 Write down the equation of the inverse of f in the form y = ....... (2)
4.4 Write down the range of y = f -1 (x). (2)
4.5 The function h(x) = (¾) x is obtained after applying two reflections on f . Write down the coordinates of B", the image of B on h. (2) [11]
QUESTION 5
The graphs of f (x) = 2 + 4 and parabola g are drawn below.
x + 1
- C, the turning point of g, lies on the horizontal asymptote of f
- The graph of g passes through the origin.
- B [ k ; 14/3] is a point on f such that BC is parallel to the y-axis.
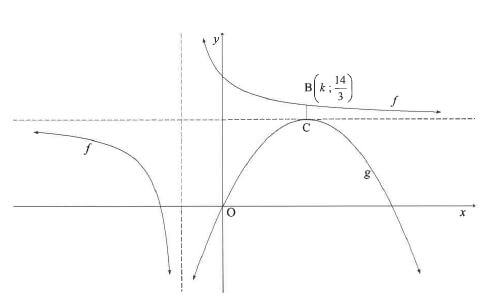
5.1 Write down the domain of f (2)
5.2 Determine the x-intercept of f (2)
5.3 Calculate the value of k (3)
5.4 Write down the coordinates of C. (2)
5.5 Determine the equation of g in the form y = a(x + p)2 + q. (3)
5.6 For which value(s) of x will f (x) < 0? (4)
g(x)
5.7 Use the graphs of f and g to determine the number of real roots of 2/x - 5 = (-x - 3)2 - 5. Give reasons for your answer. (4) [20]
QUESTION 6
6.1 Calculate how many years it will take for the value of a truck to decrease to 50% of its original value if depreciation is calculated at 15% per annum using the reducing-balance method. (4)
6.2 Every month Tshepo deposited R1 500 for his retirement into an account that paid interest at a rate of 9,2% per annum, compounded monthly. Tshepo made his first instalment on his 23rd birthday and the last instalment one month before his 55th birthday. Calculate how much money he had in the account on his 55th birthday. (5)
6.3 Abram has R150 000 to invest in two separate accounts. One account pays interest at a rate of 8,4% per annum, compounded quarterly, and the other account at a rate of 9,6% per annum, compounded monthly. How much money should he invest in each account so that he will collect the same amount from each account at the end of 12 years? (6) [15]
QUESTION 7
7.1 Given: f (x) = 2 - 3x2 Determine fi(x) from first principles. (5)
7.2 Determine:
7.2.1 D x[(4 x + 5)2 ] (3)
7.2.2 dy if y = 4√x + x2 - 8 (4) [12]
dx x2
QUESTION 8
The graph of f (x) = -x3 + 13x +12 is sketched below. A, B and D(-1 ; 0) are the x-intercepts of f. C is the y-intercept of f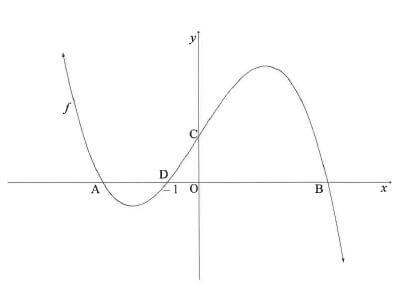
8.1 Write down the coordinates of C. (1)
8.2 Calculate the coordinates of A and B.(5)
8.3 Determine the point of inflection of g if it is given that g(x) = -f(x). (4)
8.4 Calculate the value(s) of x for which the tangent to f is parallel to the line y= -14x + c. (4) [14]
QUESTION 9
A right circular cone with radius p and height t is machined (cut out) from a solid sphere (with centre C) with a radius of 30 cm, as shown in the sketch.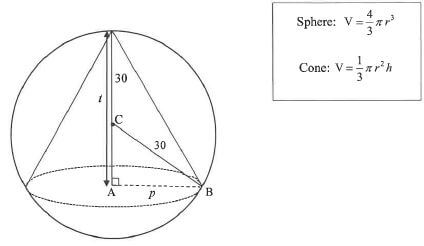
9.1 From the given information, express the following:
9.1.1 AC in terms of t. (1)
9.1.2 p2 in its simplest form, in terms of t . (3)
9.2 Show that the volume of the cone can be written as V(t) = 20πt2 - 1/3πt3 (1)
9.3 Calculate the value of t for which the volume of the cone will be a maximum. (3)
9.4 What percentage of the sphere was used to obtain this cone having maximum volume? (4) [12]
QUESTION 10
Ben, Nhlanhla, Owen, Derick and 6 other athletes take part in a 100 m race. Each athlete will be allocated a lane in which to run. The athletic track has 10 lanes.
10.1 In how many different ways can all the athletes be allocated a lane? (2)
10.2 Four athletes taking part in the event insist on being placed in lanes next to each other. In how many different ways can the lanes be allocated to the athletes now? (3)
10.3 If lanes are randomly allocated to athletes, determine the probability that Ben will be placed in lane 1, Nhlanhla in lane 3, Owen in lane 5 and Derick in lane 7 (2) [7]
QUESTION 11
A survey on their preference of exercise was conducted among 140 people in two age groups. The information is summarised below.
| AGE | TENNIS | RUNNING | GYM | TOTAL |
| 35 years and younger | a | 28 | c | 80 |
| Older than 35 years | b | 21 | d | 60 |
| 21 | 49 | 70 | 140 |
11.1 If it is given that preferring to play tennis and age are independent of each other, determine the value of a. (3)
11.2 If it is given that a = 12, determine the probability that a randomly selected person prefers going to the gym or is in the age group 35 years and younger. (5) [8]
TOTAL: 150

MATHEMATICAL LITERACY PAPER 2 GRADE 12 ADDENDUM - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICAL LITERACY
PAPER 2
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
ADDENDUM
ANNEXURE A QUESTION 3.2
ANNUAL RATES OF TAX FOR INDIVIDUALS
2017/2018 tax year (1 March 2017 to 28 February 2018)
| TAXABLE INCOME (R) | RATES OF TAX (R) |
| 0-189 880 | 18% of taxable income |
| 189 881-296 540 | 34 178 + 26% of taxable income above 189 880 |
| 296 541-410 460 | 61 910 + 31% of taxable income above 296 540 |
| 410 461-555 600 | 97 225 + 36% of taxable income above 410 460 |
| 555 601-708 310 | 149 475 + 39% of taxable income above 555 600 |
| 708 311-1 500 000 | 209 032 + 41% of taxable income above 708 310 |
| 1 500 001 and above | 533 625 + 45% of taxable income above 1 500 000 |
TAX REBATES
| TAX REBATE | TAX YEAR |
| 2017/2018 | |
| Primary | R13 500 |
| Secondary (65 and older) | R7 407 |
| Tertiary (75 and older) | R2 466 |
[Source: SARS Last Updated: 30/06/2017 12:47]
ANNEXURE B
QUESTION 3.3.1
Layout of the parts of toy storage boxes on ONE sheet of plywood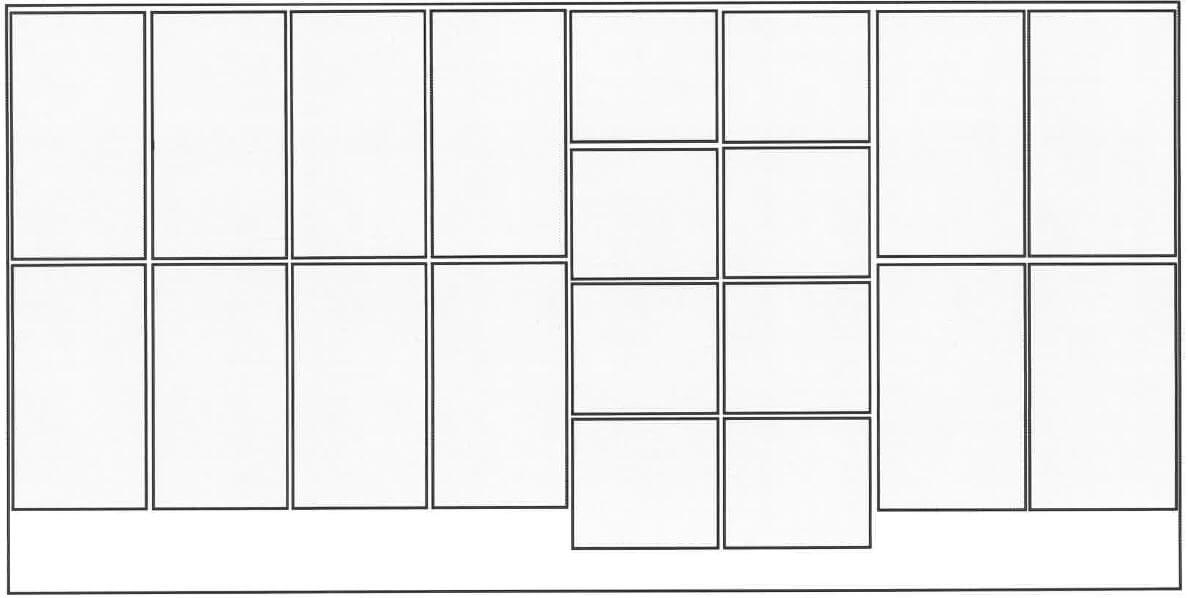
ANNEXURE C
QUESTION 3.3.3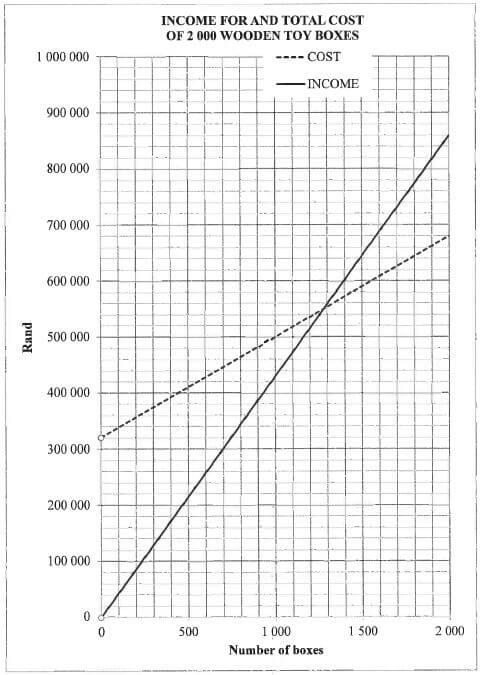
ANNEXURE D
QUESTION 4.1
PART OF THE MAP OF THE KRUGER NATIONAL PARK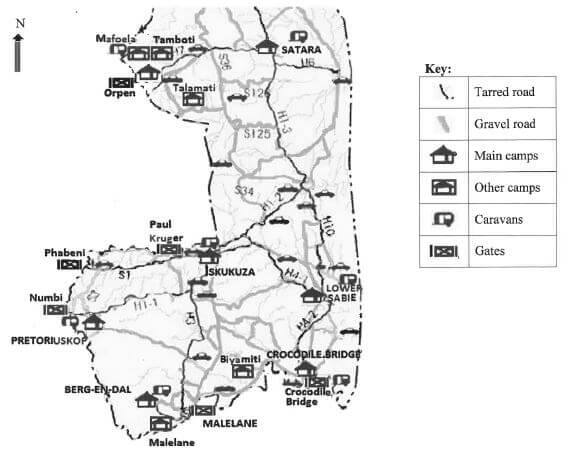
[Adapted from http//krugerrnationalpark.co.za]
TABLE 4: Distances between camps and gates in the Kruger National Park
| Gates and camp distances | Berg-en-dal | Lower Sabie | Malelane | Mopani | Numbi Gate | Orpen | Pafuri Gate | Pretoriuskop | Satara | Skukuza |
| Berg-en-dal | - | 113 | 12 | 281 | 97 | 213 | 453 | 92 | 165 | 172 |
| Lower Sabie | 113 | - | 105 | 209 | 95 | 141 | 380 | 90 | 93 | 43 |
| Malelane | 12 | 105 | - | 272 | 94 | 204 | 444 | 85 | 156 | 64 |
| Mopani | 281 | 209 | 272 | - | 263 | 164 | 172 | 258 | 116 | 209 |
| Numbi Gate | 97 | 95 | 94 | 263 | - | 195 | 434 | 9 | 147 | 54 |
| Orpen | 213 | 141 | 204 | 164 | 195 | - | 335 | 184 | 48 | 137 |
| Pafuri Gate | 453 | 380 | 444 | 172 | 434 | 335 | - | 438 | 287 | 380 |
| Paul Kruger Gate | 83 | 53 | 74 | 220 | 65 | 152 | 392 | 60 | 104 | 12 |
| Pretoriuskop | 92 | 90 | 85 | 258 | 9 | 184 | 438 | - | 140 | 49 |
ANNEXURE E QUESTION 4.3
AVERAGE DAILY RATES AND OCCUPANCY FOR DIFFERENT REGIONS FROM 2010 TO SEP. 2015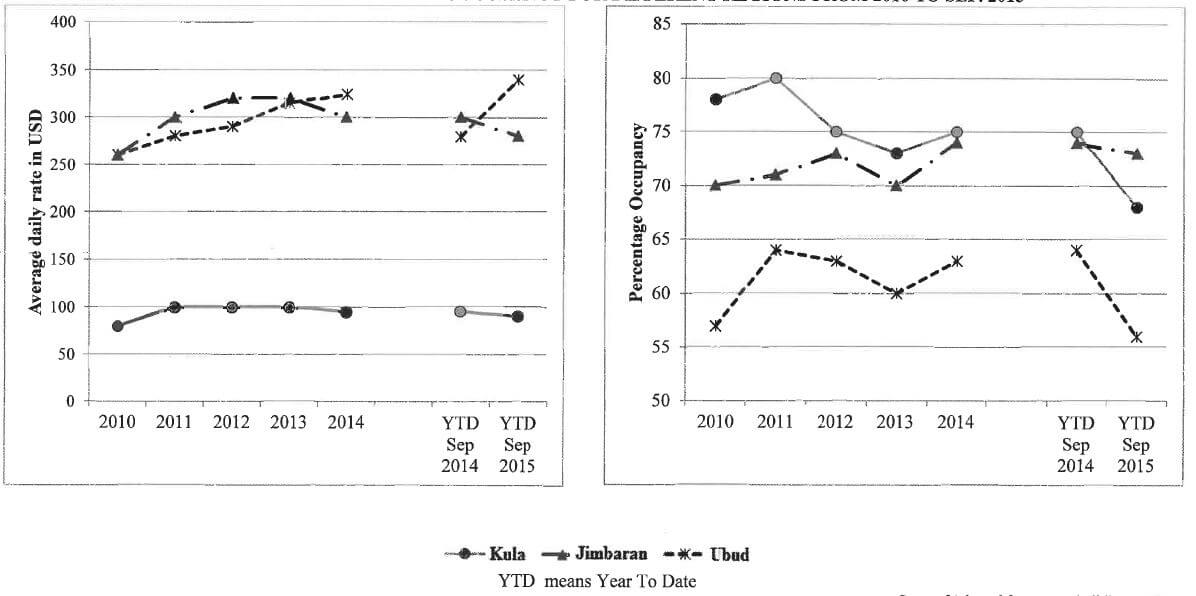
Source:[Adapted from www.balidiscovery.com]
MATHEMATICAL LITERACY PAPER 1 GRADE 12 ADDENDUM - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICAL LITERACY
PAPER 1
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
ADDENDUM
ANNEXURE A
UESTION 2.1
| GEMS | MEMBER - MRS CHAN: 3526178 | STATEMENT REFERENCE: A356748 DOCUMENT REFERENCE: 5109725 | DATE 15/12/17 STATEMENT 187992 | ||||||||||
| Transaction information | Payment information | ||||||||||||
| Date treated | Patient | Tarriff code | Amount claimed | Benefir approved | Scheme paid supplier | Scheme paid member | Member owes scheme | Member paid/ owes supplier | See below | Amount paid in hospital benefit | Amount paid from other limits | Tax claimable amount | |
| DIS-CHEM PHARMACY 098 234 (Chemist) | |||||||||||||
| 08/12/17 | Lee | Acute | 736, 90 | 9505 | |||||||||
| 08/12/17 | Lee | Chronic | 173, 03 | 173, 03 | 173, 03 | 173, 03 | |||||||
| 08/12/17 | Lee | Chronic | 117, 44 | 117, 44 | 117, 44 | 117, 44 | |||||||
| 08/12/17 | Lee | Chronic | 61, 50 | 61, 50 | 61, 50 | 61, 50 | |||||||
| 08/12/17 | Lee | Chronic | 80, 98 | 80, 98 | 80, 98 | 80, 98 | |||||||
| 08/12/17 | Lee | Chronic | 46, 80 | 46, 80 | 46, 80 | 46, 80 | |||||||
| Dhlamini M DR 1627805 (General Practitioner) | |||||||||||||
| 08/12/17 | Lee | 0192 | 343,00 | 343,00 | 870 | 343,00 | |||||||
| 09/12/17 | Lee | 0132 | 102,10 | 102,10 | 870 | 102,10 | |||||||
| Totals: | 1, 661, 75 | 479, 75 | 445, 10 | 445, 10 | |||||||||
| Summary of Financial Information | |
| Payable to Member (Credit) | 0,00 |
| Less owed to Scheme (Debit) | 0,00 |
| Member to pay Supplier(s) (Debit) | 445,10 |
| Tax claimable to date | 5326,66 |
| Summary of codes | |
| 870 | Overall Limit Exceeded |
| 9505 | Pre authorisation required |
ANNEXURE B
QUESTION 4.1
LAYOUT PLAN OF THE SHOPPING MALL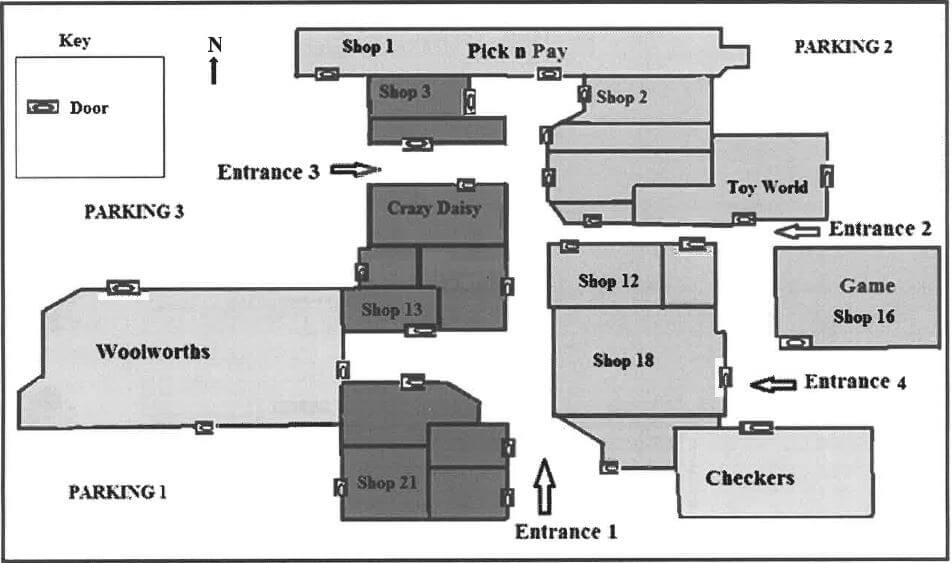
[Adapted from www.thenewoakparkmall.com]
ANNEXURE C
QUESTION 5.2 PIE CHARTS SHOWING THE DIFFEERENT SOURCES OF INCOME FOR TWO PROVINCES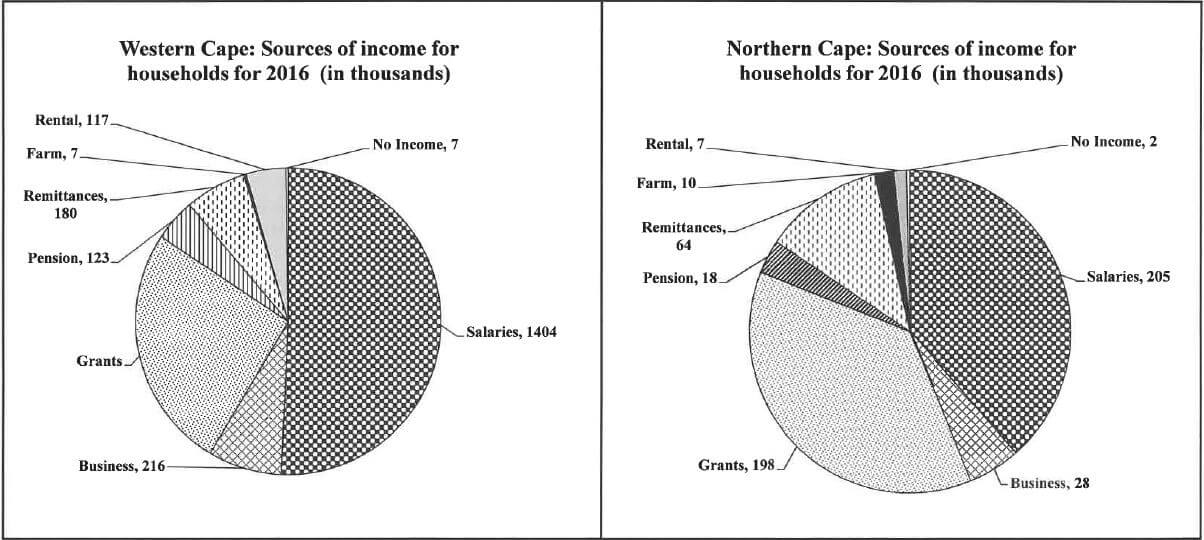
[Adapted from www.statssa.co.za]
MATHEMATICAL LITERACY PAPER 1 GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICAL LITERACY
PAPER 1
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
SYMBOL | EXPLANATION |
M | Method |
MA | Method with accuracy |
MCA | Method with consistent accuracy |
CA | Consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
RT/RG/RP | Reading from a table/graph/plan |
SF | Correct substitution in a formula |
O | Opinion/Example/Definition/Explanation |
P | Penalty, e.g. for no units/incorrect rounding off, etc. |
R | Rounding off |
NPR | No penalty rounding or omitting units |
AO | Answer only, if correct, full marks |
NOTE:
- If there is an additional incorrect answer mark as follows:
- If the solution contains the word “OR”, then penalty of 1 mark
- If the solution contains the word “AND”, then mark only the first solution with a penalty of 1 mark.
MEMORANDUM
Question 1 [31 MARKS]AO Full Marks | |||
Ques | Solution | Explanation | T/L |
1.1.1 | Horizontal/double/compound/multiple ✓O bar graph ✓O | 1O type | D |
1.1.2 | ✓RT | 1RT reading all correct values | D |
1.1.3 | Step 6 ✓✓A | 2A identifying correct Step | F |
1.1.4 | Cape Town ✓✓A | 2A stating Cape Town | F |
1.1.5 | ✓RT | 1RTfor R7,14 | F |
1.1.6 | Numerical ✓✓A | 2A stating numerical | D L1 |
1.2.1 | Selling price minus profit ✓✓A | 2A correct definition
| F L1 |
1.2.2 | ✓RT ✓A | 1RT correct values | F |
Ques | Solution | Explanation | T/L |
1.2.3 | ✓A | 1A correct hours | M |
1.2.4 | ✓MA | 1MA adding all correct values | F |
1.3.1 | Converting scale reading | 1M dividing by 1 000 | M |
1.3.2 | ✓M | 1M subtracting correct values | M |
1.3.3 | ✓M ✓M ✓A OR Plum = 128 g ÷ 2 ✓M | 1M subtraction from 394 OR 1Mdividing pear by 2 | M |
1.3.4 | 0% OR 0 OR0 ✓✓A | 2A solution | P |
1.3.5 | 394g : 128g ✓M | 1M concept of ratio
| M |
[31] |
QUESTION 2 [38MARKS] | |||
Ques | Solution | Explanation | T/L |
2.1.1 | December ✓✓A The last month of the year ✓✓ A | 2A correct month
| F L1 |
2.1.2 | The overall limit exceeded ✓✓A | 2A correct code description
| F L1 |
2.1.3 | Dr Dhlamini ✓✓RT | 2RT name (2) | F |
2.1.4 | ✓MA OR ✓MA | 1MA calculating 6,3% OR 1MA calculating 106,3% | F L2 |
Ques | Solution | Explanation | T/L | ||
2.1.5 | ✓ RT | AO | F L2 | ||
2.1.6 | ✓✓O | 2O for correct definition | F L1 | ||
Accept: Full Marks Amount of money not paid by the scheme. Money owed to the scheme. | |||||
(2) | |||||
2.1.7 | Total amount ✓RT ✓M =R173,03 + R117,44 + R61,50 +R80,98 + R46,80 OR Total amount ✓RT ✓M | 1RT all correct values OR 1RT all correct values | F L1 | ||
2.2.1 | Value Added Tax ✓✓A | 2A acronym written out (2) | F | ||
2.2.2 | ✓RT OR ✓RT OR ✓RT | 1RT using correct value OR 1RT using correct value OR 1RT using correct value 1M dividing by 1,14 and subtracting | F L2 | ||
Ques | Solution | Explanation | T/L |
2.2.3 | Difference = R223 - R13 ✓M | AO
| F L1 |
2.3.1 | Exchange rate | 2RT correct exchange rate (2) | F L1 |
2.3.2 | Rupee✓A | 1A rupee
| L1 F |
2.3.3 a | Cost price = ZAR 13 × 0,797782 ✓M | AO OR 1M dividing correct values | F L2 |
2.3.3 b | Profit = (SP - CP) × number sold | CA from Q2.3.3a | F L3 |
Ques | Solution | Explanation | T/L |
2.3.4 | Number of shares 3+2 =5✓A | AO | F L2 |
2.3.5 | ✓A | 1Anumerator | F L2 |
[38] |
QUESTION 3 [21 MARKS] | |||
Ques | Solution | Explanation | T/L |
3.1.1 | Number of pallets = 12 × 2✓MA | AO | M L1 |
3.1.2 | Height of the table ✓RT | 1RT using correct values
| M L1 |
3.1.3 | Area = length × width | 1RT reading of correct values | M L2 |
3.1.4 | Perimeter of glass top OR ✓M | AO OR 1M correct formula | M L1 |
Ques | Solution | Explanation | T/L |
3.2.1 | Length of ribbon OR Length of ribbon | 1C converting diameter to 11 cm OR 1SF substituting in formula | M L2 |
3.2.2 a | Inner diameter = 110 - 5 - 5 | AO | M L1 |
3.2.2 b | Volume of cylinder | CA from Q3.2.2 a | M L2 |
[21] |
QUESTION 4 [25MARKS] | |||
Ques | Solution | Explanation | T/L |
4.1.1 | 7 ✓✓RP | 2RP correct store number | MP L1 |
4.1.2 | Parking 2 ✓✓RP | 2RP correct parking number | MP L1 |
4.1.3 | Woolworths✓✓RP | 2RP correct shop name
| MP L1 |
4.1.4 | Turn right as you exit the Crazy Daisy Shop✓A OR Turn right as you exit the Crazy Daisy Shop ✓A Turn right towards Entrance 1 ✓A Turn left passing Checkers heading towards Entrance 4 | 1A turn right OR 1A turn right
| MP L2 |
Ques | Solution | Explanation | T/L |
4.1.5 | 27 doors ✓✓A | 2A correct number of doors (2) | MP |
4.1.6 | ✓A | 1A numerator Max 1 mark for 3 (2) | P L2 |
4.1.7 | ✓A | 1A numerator | P L2 |
Ques | Solution | Explanation | T/L |
4.2.1 | Top view of the coffee shop. ✓✓A | 2A explanation
| MP L1 |
4.2.2 | Bathroom OR Wash roomOR Rest room ✓✓RP | 2RP reading from plan
| MP L1 |
4.2.3 | South-East / SE ✓✓RP | 2RP reading from plan (2) | MP L1 |
4.2.4 | 70 mm : 15 m | 1C convert to mm | MP L3 |
[25] |
QUESTION 5 [35 MARKS] | ||||
Ques | Solution | Explanation | T/L | |
5.1.1 | September ✓✓RT | 2RT read from table
| D L1 | |
5.1.2 | Mean income | 1RT correct values | D L2 | |
5.1.3 | ✓RT | 1RT correct values | D L1 | |
5.1.4 | 45 905 000 ✓✓RT | 2RT correct value from table | D L1 | |
5.1.5 | ✓RT | 1RT reading from table as is 1A correct wording with millions (2) | D L1 | |
5.1.6 | ✓MA | AO | D L2 | |
5.1.7 | ✓A P(less than 200 000 000) = 1 | AO | P L2 | |
Ques | Solution | Explanation | T/L | |
5.1.8 | 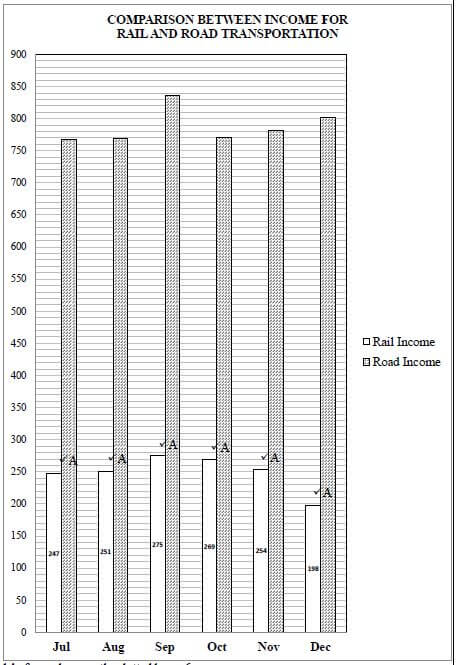 | D L2 | ||
1A for each correctly plotted bar × 6 | ||||
Ques | Solution | Explanation | T/L |
5.2.1 | Total number of households for Grants: | 1M subtracting from 2 768 | D L1 |
5.2.2 | Business ✓✓RG | 2RG correct source (2) | D L1 |
5.2.3 | Difference | AO | D L1 |
5.2.4 | Remittance | 1RT correct values | D L2 |
[35] | |||
TOTAL: 150 MARKS | |||
MATHEMATICAL LITERACY PAPER 2 GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICAL LITERACY
PAPER 2
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
Symbol | Explanation |
M | Method |
MA | Method with accuracy |
CA | Consistent accuracy |
A | Accuracy |
C | Conversion |
S | Simplification |
RT | Reading from a table/a graph/document/diagram |
SF | Correct substitution in a formula |
O | Opinion/Explanation/Opinie |
P | Penalty, e.g. for no units, incorrect rounding off, etc. |
R | Rounding off |
NPR | No penalty for rounding |
AO | Answer only |
MCA | Method with constant accuracy |
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- If a candidate has crossed out (cancelled) an attempt to a question and NOT redone the solution, mark the crossed out (cancelled) version.
- Consistent accuracy (CA) applies in ALL aspects of the marking guideline, however it stops at the second calculation error.
- If the candidate presents any extra solution when reading from a graph, table, layout plan and map, then penalise for every extra item presented.
MEMORANDUM
QUESTON/1 [35 MARKS] | |||
Q/V | Solution | Explanation | T&L |
1.1.1 | A = 367 × 3 ✓M | 1M multiplying OR 1M working with ratio | D L2 |
1.1.2 | 1 Teacher + 3 learners = 4 persons ✓A | 1A total persons | D L2 |
1.2.1 | ✓RT ✓RT | 2RT correct values | D L2 |
1.2.2 | Mean % | 1MA adding correct values | D L2 |
Q/V | Solution | Explanation | T&L |
1.2.3 | IQR = Upper quartile - Lower quartile ✓A | 1A value of Q3 | D L3 |
1.2.4 | ✓✓O The minimum Matuli scored was 48% which is better than Bianca's 36%. | 2O comparing mean marks | D L4 |
1.3.1 | Probability of randomly choosing an Indian | 1A numerator | P L4 |
Q/V | Solution | Explanation | T&L |
1.3.2 | Difference = Rs40 000 ✓A OR ✓MA ✓MA OR R1 ÷ 0,081 = R12,35 ✓A | 1A difference OR 1MA convert to dollars OR 1A rand per dollar ratio | F L3 |
1.3.3 | Change received | 1MA difference 1O not valid (4) | F L4 |
[35] |
QUESTION 2 [38MARKS] | |||
Q/V | Solution | Explanation | T&L |
2.1.1 | Right-hand side OR Western side ✓✓A | 2A correct side(2) | M&P L2 |
2.1.2 (a) | 140 mm : 3 500 mm ✓MA | 1MA values in correct order | M&P L3 |
2.1.2 (b) | Length/Lengte = 6 000 ÷ 25 ✓MCA OR 140 : 3 500 | CA from 2.1.2(a) OR 1M concept of proportion | M&P L3 |
2.1.3 | Side door area | 1SF substitution | M L2 |
Q/V | Solution | Explanation | T&L |
2.1.4 | 41 410 000 mm2 = 41,410 m2 ✓C OR 41 410 000 mm2 = 41,410 m2 ✓C OR ✓C | 1C converting to m2 OR 1C converting to m2 OR 1C converting to mm2 | M L3 |
2.1.5 | Cost | CA from Q2.1.4 | F L4 |
Q/V | Solution | Explanation | T&L |
2.1.6 | SI = Principal amount × interest rate × time in years | 1SF substituting correct values OR 1SF substitution | F L3 |
2.2.1 | 1 foot = 12 inches OR 6 m = 6 000 mm OR ½ inch = 12,7mm✓MA OR ✓A | 1M multiplying OR 1M divide OR 1MA use of proportion | M L4 |
2.2.2 | ✓A | 1A radius | M L3 | ||
[38] | |||||
QUESTION [38MARKS] | |||
Q/V | Solution | Explanation | T&L |
3.1.1 | Local share | 1MA calculating 20,12% | F L2 |
3.1.2 | Percentage increase OR Percentage ✓RT | 1RT reading correct values OR 1RT correct values | F L2 |
3.1.3 | National government sector services the whole country and not just one province. ✓✓O | 2O explanation (2) | F L4 |
Q/V | Solution | Explanation | T&L |
3.1.4 | Total ratio | 1MA adding ratio values | F L3 |
3.2 | Annual taxable income | 1A annual taxable income | F L3 |
Q/V | Solution | Explanation | T&L |
3.3.1 | 4 ✓✓A | 2A number of boxes (2) | MP L2 |
3.3.2 | Number of sheets = 2750 ✓M OR Number of boxes = 687 × 4 ✓M OR Number of boxes per sheet ∴ Not enough ✓O | CA from 3.3.1 OR 1M multiplying OR 1M dividing | MP L4 |
3.3.3 (a) | Income per box | 1RT reading correct value | F L2 |
3.3.3 (b) | ✓✓RT | 2RT estimation | F L3 |
Q/V | Solution/Oplossing | Explanation/Verduideliking | T&L |
3.3.3 (c) | Variable cost per box Income = R430 × 2750 ✓M | 1CA using ANY TWO cost values or from Q3.3.3.(a)/(b) | F L4 |
[38] |
QUESTION 4 [39MARKS] | |||
Q/V | Solution | Explanation | T&L |
4.1.1 | Staff working at the gates need to go home. ✓✓O | 2O 1st reason | D L4 |
4.1.2 | Skukuza ✓✓A | 2A correct camp (2) | MP L2 |
4.1.3 | Orpen to/na Satara 48 k✓RT | 1RT distance to Satara | MP L3 |
4.1.4 | Main camps = 7 ✓RT | 1RT number of both camps | MP L2 |
Q/V | Solution | Explanation | T&L |
4.1.5 | Distance = speed × time | 1RT distance | M L3 |
4.1.6 | The roads are not so busy / people drive slower / more animals are visible. ✓✓O | 2O reason (2) | MP L4 |
4.2.1 | ✓A | 1A numerator | P L2 |
Q/V | Solution/Oplossing | Explanation/Verduideliking | T&L |
4.2.2 | Coloured Employees | 1MA finding the missing value | P L3 |
4.3.1 | ✓RT ✓RT | 1RT Jimbaran (255 - 265) | F L2 |
4.3.2 | ✓O ✓O | 1O decrease | D L4 |
4.3.3 | The average daily rates in Ubud had a increase. ✓✓O | 2O magnitude of the increase | D L4 |
4.3.4 | The first part of the graph represents the years 2010 to 2014/ or number of years. ✓✓O | 2O explanation of the first part | D L4 |
[39] | |||
TOTAL :150 | |||
MATHEMATICAL LITERACY PAPER 2 GRADE 12 QUESTIONS - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICAL LITERACY
PAPER 2
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of FOUR questions. Answer ALL the questions.
- Use the ANNEXURES in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 3.2
- ANNEXURE B for QUESTION 3.3.1
- ANNEXURE C for QUESTION 3.3.3
- ANNEXURE D for QUESTION 4.1
- ANNEXURE E for QUESTION 4.3
- Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Round off ALL final answers appropriately according to the given context, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Maps and diagrams are NOT drawn to scale, unless stated otherwise.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1
In a national science olympiad the rules state that each school may enter a maximumof three learners (participants). TABLE 1 below shows the relationship between the number of schools entering and the maximum number of participants.
|
Use the information above to answer the questions that follow.
1.1.1 Determine the missing values A and B. (4)
1.1.2 Each school must have ONE teacher who invigilates the writing of the olympiad. Calculate the number of schools that entered the olympiad if a total of 32 712 people were involved on the day the olympiad was written. (3)
1.2
Matuli, Bianca and Khotso wrote some practice tests at their school. Their percentage marks are given in the table below.
NOTE:
|
Use the information above to answer the questions that follow.
1.2.1 Calculate Matuli's median percentage mark. (4)
1.2.2 Calculate Bianca's mean percentage mark (3)
1.2.3 The box and whisker diagram below represents the spread of Khotso's percentage marks.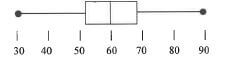
Determine the missing value C, the lower quartile mark, if Khotso's interquartile range (IQR) is 16.
The following formula may be used:
IQR = Upper quartile — Lower quartile (3)
1.2.4 Bianca stated that Matuli performed better than she did in the practice tests. Give TWO possible reasons to support Bianca's statement. (4)
1.3
45 hundred thousand students from 25 different countries participated in an-international mathematics olympiad. There were 171 Indian students who received awards.
NOTE:
[Source: x-rates.com/calculator, 2018/01/04] |
Use the information above to answer the questions that follow.
1.3.1 Vijay stated that the probability (as a percentage) of randomly choosing an Indian student that received an award out of the total number of students was less than 0,004%. Determine, showing ALL calculations, if his statement is correct. (5)
1.3.2 Determine the difference (in South African rand) between the amounts received for 1St position and 3rd position. (5)
1.3.3 Currently bank notes in India are issued in the following denominations:
Rs10; Rs20; Rs50; Rs100; Rs200; Rs500; Rs2 000
Vijay bought a tablet worth Rs2 440. He paid for it with TWO Rs2 000 bank notes. He stated that he would receive a minimum of 6 bank notes as change. Verify whether his statement is valid. (4) [35]
QUESTION 2
2.1 
Use the information above to answer the questions that follow.
2.1.1 Zanele enters the garage through the side door. Determine on which side of Zanele the garage door will be found. (2)
2.1.2 On a scaled drawing of the garage, the width is 140 mm.
Determine:
- The scale of the drawing (3)
- The length (in cm) of the garage on the scaled drawing (3)
2.1.3 Determine the total area (in mm2) of the openings (unbricked sections) of the garage walls. (6)
2.1.4 Calculate the number of brick pallets needed to build this garage if the total area of the bricked section of the garage is 41 410 000 mm`. (6)
2.1.5 Japie states that the bricks, doors and window will cost him approximately R12 500. Verify (showing ALL calculations) whether his statement is valid. (4)
2.1.6 Japie borrowed R35 000 from an uncle to complete the building of the garage. The terms for the loan were to repay the full amount including simple interest at a rate of 8% per annum after 7 months. Calculate how much he must pay back 7 months after the loan was granted. The following formula may be used:
Simple interest = principal amount x interest rate x time in years (3)
2.2
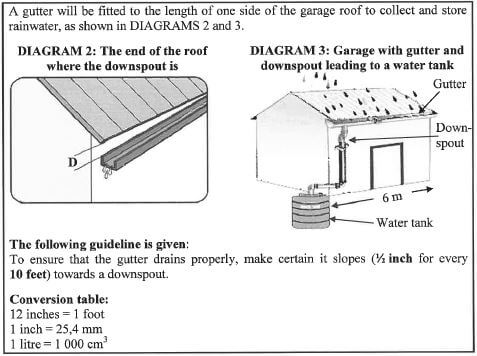
A gutter will be fitted to the length of one side of the garage roof to collect and store rainwater, as shown in DIAGRAMS 2 and 3. |
2.2.1 Calculate how much lower (in mm) the gutter will be at the end where the downspout is, in other words calculate D in DIAGRAM 2. (6)
2.2.2 Calculate the capacity (in litres) of a cylindrical water tank with a diameter of 80 cm and a height of 1,2 m.
The following formula may be used:
Volume of a cylinder = ir x (radius)2 x height using 2t = 3,142 (5) [38]
QUESTION 3
3.1.
TABLE 3 below shows the distribution of revenue among the different government sectors in South Africa for the period 2013/14 to 2017/18. Some values have been omitted
[Adapted from Treasury.gov.za] | |||||||||||||||||||||||||||||||||||||||
Use the information above to answer the questions that follow.
3.1.1 When the revenue of the local government sector was compared to the provincial government sector in 2013/14, it was found to be 20,12% of the provincial sector. Calculate the missing value E, the total revenue for the period 2013/14. (4)
3.1.2 Determine the percentage by which the revenue for the national government sector increased during the period 2014/15 to 2015/16. (3)
3.1.3 Explain why the national government sector received more revenue than the other sectors. (2)
3.1.4 Calculate the revenue allocated to the local government sector for the period 2017/18 if the distribution of revenue among the different sectors was done according to the following ratio:
Local : Provincial : National = 1 : 4,784 : 5,246 (4)
3.2 One of the major sources of revenue for the government is personal income tax. The tax table for 2017/2018 is given on ANNEXURE A. Landy, a 57-year-old lady, received an average monthly taxable income of R46 308,50 for the 2017/2018 tax year and she is not a member of a medical aid scheme. Determine how much tax Landy has to pay every month. (7)
3.3
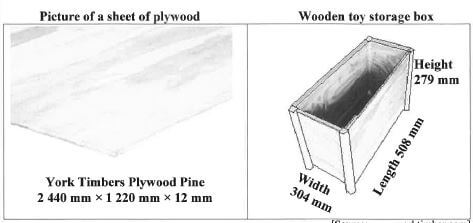
Landy has a contract to deliver 2 750 wooden toy storage boxes without lids. |
Use the information above and ANNEXURE B to answer the questions that follow.
3.3.1 Determine how many complete boxes can be cut from ONE sheet of plywood. (2)
3.3.2 Verify, showing ALL calculations, whether 687 sheets of plywood will be enough to make 2 750 boxes. (3)
3.3.3 Landy employed a carpenter (a person who works with wood) to make the 2 750 boxes for her. Her total cost for the manufacture of the boxes consisted of fixed costs (labour) plus variable costs (plywood, varnish, screws and glue). She drew income and total cost graphs, as shown on ANNEXURE C. ANNEXURE C shows the projected income and total cost for only 2 000 boxes.
- Calculate the income amount per box. (3)
- Estimate the number of boxes required to break even. (2)
- Landy projected the total profit from ALL the boxes to be R367 500. (8) [38]
Verify if her projection is valid.
QUESTION 4
4.1
The Kruger National Park is a popular tourist destination. Some information about the park is given below:
Gate times:
ANNEXURE D shows a part of the map of the Kruger National Park and TABLE 4 shows the distances between the camps and gates. |
Use the information above and ANNEXURE D to answer the questions that follow.
4.1.1 Give TWO possible reasons why there are specific times for the gates to open and close. (4)
4.1.2 Ludwe enters the Park through the gate located northwest of Crocodile Bridge, which has no camp. He travels in as easterly direction until he finally reaches the first camp. Write down Ludwe's final destination. (2)
4.1.3 Show (by calculation) that the distance shown on the distance table from Orpen to Lower Sabie, is the route via Satara. (3)
4.1.4 Determine the difference in the number of main camps and other camps on this part of the map. (2)
4.1.5 Ludwe left Skukuza at 17:03 and had to be out of the park through the Malelane Gate before 18:30 the same day. The distance on the gravel road is the same as the distance on the tarred road. Calculate at what time he would reach the Malelane Gate if he used the gravel road.
The following formula may be used:
Distance = speed X time (6)
4.1.6 Give a possible reason why most people visiting the park prefer to travel on the gravel roads than on the tarred roads. (2)
4.2
| TABLE 5 below shows the number of employees at the South African National Parks (SANP), according to race and employment levels. TABLE 5: NUMBER OF SANP EMPLOYEES ACCORDING TO RACE AND EMPLOYMENT LEVEL
| ||||||||||||||||||||||||||||||||||||
Determine the probability of randomly selecting the following:
4.2.1 An Indian employee from the SANP employees (2)
4.2.2 A Coloured employee from the total employment level B employees (3)
4.3
| Bali is an international tourist destination that consists of different regions. The graphs on ANNEXURE E show the average daily rate and percentage occupancy. [Percentage occupancy is the percentage of all rental units that are rented out at a given time.] |
Use ANNEXURE E to answer the questions that follow.
4.3.1 Calculate the difference between the average daily rates in Jimbaran and Kula during 2010. (3)
4.3.2 The average daily rate in Kula remained almost the same from 2011 to 2014. Explain your observations regarding the percentage occupancy in Kula during the same period. (4)
4.3.3 Compare the relationship between the average daily rates and the percentage occupancy in Ubud for the year to date (YTD) Sep. 2014 to YTD Sep 2015. (4)
4.3.4 Explain why both graphs have a gap between 2014 and YTD September 2014. (4) [39]
TOTAL: 150
MATHEMATICAL LITERACY PAPER 1 GRADE 12 QUESTIONS - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MATHEMATICAL LITERACY
PAPER 1
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions. Answer ALL the questions.
-
- 2.1 Use the ANNEXURES in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 2.1
- ANNEXURE B for QUESTION 4.1
- ANNEXURE C for QUESTION 5.2
- 2.2 Answer QUESTION 5.1.8 on the attached ANSWER SHEET.
- 2.3 Write your centre number and examination number in the spaces on the ANSWER SHEET. Hand in the ANSWER SHEET with your ANSWER BOOK.
- 2.1 Use the ANNEXURES in the ADDENDUM to answer the following questions:
- Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Round off ALL final answers appropriately according to the given context, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise.
- Write neatly and legibly.
QUESTION 1
1.1

[Adapted from www.graphics24.co.za]
1.1.1 State the type of graph used to represent this data. (2)
1.1.2 Arrange Cape Town's percentage increase in descending order. (2)
1.1.3 Identify the step that indicates the largest increase (in rand) in Cape Town's water tariff from 2016/17 to 2017/18. (2)
1.1.4 Determine in which ONE of the two cities water is more expensive. (2)
1.1.5 Calculate the cost of 3,5 kC of water in Johannesburg during 2017/18. (2)
1.1.6 Is the data given categorically or numerically? (2)
1.2 
[Adapted from www.pricecheck.co.za]
1.2.1 Explain the term cost price. (2)
1.2.2 Calculate the cost price of CLOCK A, excluding VAT. (2)
1.2.3 Write down the time on CLOCK B, using the 24-hour format if it represents the time in the evening. (2)
1.2.4 Calculate the total profit made if all four clocks are sold. (2)
1.3
[Adapted from www.pricecheck.co.za]
Use the photograph and information above to answer the questions that follow.
1.3.1 Convert the total mass of the fruit into kg. (2)
1.3.2 The pear is removed from the kitchen scale. Write down the new reading (in grams) shown on the kitchen scale. (2)
1.3.3 Show how the mass of 202 g for the peach was calculated. (3)
1.3.4 Determine the probability of randomly selecting a banana from the fruit placed on the kitchen scale. (2)
1.3.5 Write down the simplified ratio of the total mass of fruit to the total mass of the pear. (2) [31]
QUESTION 2
2.1
| Mrs Chan, a teacher from Brakpan, received a monthly statement from GEMS (Government Employee Medical Scheme), as shown in ANNEXURE A. Mrs Chan has one dependent, her son Lee, on her medical aid. |
Use ANNEXURE A to answer the questions that follow.
2.1.1 Which month is covered by this statement? (2)
2.1.2 State why the member had to pay R445,10 to the supplier. (2)
2.1.3 Write down the name of the general practitioner visited. (2)
2.1.4 Calculate the new price of the acute medication (under the tariff code) if the price increased by 6,3%. (3)
2.1.5 Calculate the total amount of tax claimable in the previous statements if the tax claimable is the amount paid by the member directly to the supplier. (2)
2.1.6 Define the term debit within the context of the statement. (2)
2.1.7 Show how the total amount of R479,75 was calculated. (2)
2.2
[Source: www.wish.com
Study the advertisement above and answer the questions that follow.
2.2.1 What does the acronym VAT stand for? (2)
2.2.2 Calculate the amount of VAT payable on the old price for the PPH. (3)
2.2.3 Calculate the difference between the new price and the old price of the UTM. (2)
2.3
John told his friend Errol, who lives in Botswana, about the profit he made when he sold the ultra-thin mouse (UTM).
[Source: www.x-rates.com] |
Use the table and the information above to answer the questions that follow.
2.3.1 Write down the exchange rate between the Botswana pula (BWP) and the South African rand (ZAR). (2)
2.3.2 List the currencies which are weaker than the ZAR. (3)
2.3.3 Each mouse costs R13,00 and is sold for BWP48.
- Convert R13,00 into BWP (2)
- Calculate the total number of UTMs sold if a total profit of BWP7526 was made. (4)
2.3.4 Calculate the amount (in BWP) that Errol will receive if a total profit of BWP7526 was made. (3)
2.3.5 Show how the Algerian dinar of 0,104747 ZAR per unit was obtained. (2) [38]
QUESTION 3
3.1
[Adapted from www.pintrest.com
Use the information and photographs above to answer the questions that follow. (2)
3.1.1 Calculate the number of pallets needed to produce 12 tables. (3)
3.1.2 Calculate the total height of the table, excluding the glass top, if the leg, including the wheel, is 200 mm high. (3)
3.1.3 Calculate the area (in mm2) of the glass top.
You may use the formula:
Area = length x width (3)
3.1.4 For safety reasons a rubber strip will be placed around the edge of the glass top. Calculate the total length (in mm) of rubber required for this purpose. (3)
3.2
[Adapted from www.pintrest.com]
Use the information above to answer the questions that follow.
3.2.1 The holder will have a decorative ribbon around it. The ribbon will be 2 cm longer than the circumference of the holder so that a bow can be tied in the ribbon. Calculate the total length (in cm) of ribbon needed for one holder. You may use the following formula:
Total length of ribbon = ir x diameter + overlap, and using it = 3,142 (4)
3.2.2
- Write down the inner radius (in mm) of the cylindrical holder. (2)
- Hence, calculate the space needed in the holder to fit exactly 8 coasters.
You may use the following formula:
Volume of cylinder = it x radius2 x height; and using it = 3,142 (4) [21]
QUESTION 4
4.1
| Crazy Daisy Coffee Shop is situated in the north wing of a shopping mall. The layout plan (drawn to scale) of the shopping mall is given in ANNEXURE B. |
Use ANNEXURE B to answer the questions that follow.
4.1.1 Write down the shop number of Crazy Daisy Coffee Shop. (2)
4.1.2 State which parking area is closest to Toy World. (2)
4.1.3 Write down the name of the shop which has the biggest floor area. (2)
4.1.4 The manager of shop 18 ordered a cup of coffee and a slice of cake to be delivered by Crazy Daisy Coffee Shop. Give the delivery man a set of directions from Crazy Daisy Coffee Shop up to the entrance of shop 18. (4)
4.1.5 Calculate the total number of doors shown on this layout plan. (2)
4.1.6 Write down the probability of randomly selecting a shop that has TWO door entrances. (2)
4.1.7 Determine the probability of randomly selecting a shop that is NOT labelled with an even number. (2)
4.2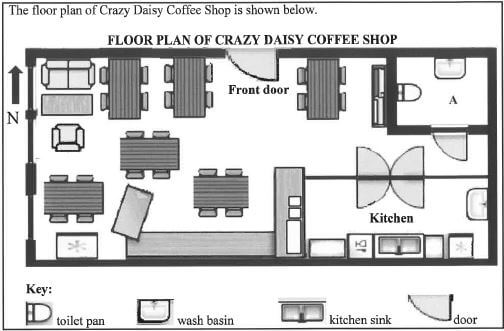
[Adapted from www.shopkeep.com
Use the floor plan above to answer the questions that follow.
4.2.1 Explain the meaning of the term floor plan. (2)
4.2.2 Identify the room labelled A. (2)
4.2.3Give the general direction of the kitchen from the front door. (2)
4.2.4 The measured width of the coffee shop is 70 mm. The actual width is 15 m. Determine the scale (rounded off to the nearest whole number) of the floor plan. (3) [25]
QUESTION 5
5.1
| Statistics South Africa (STATSSA) collects and releases data based on passenger transport annually. TABLE 2 below shows the 2016 data for land passenger transportation. TABLE 2: 2016 DATA FOR LAND PASSENGER TRANSPORT
[Adapted from www.statssa.co.za] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Use the table above to answer the questions that follow.
5.1.1 Write down the month with the highest income for rail transportation. (2)
5.1.2 Calculate the mean monthly income for rail transportation. (3)
5.1.3 Calculate the road transportation income for April as a percentage of the total land income. (3)
5.1.4 Write down the total number of land passenger journeys for December. (2)
5.1.5 Write down (in words) the total number of passenger journeys for September. (2)
5.1.6 Calculate the median total land income. (3)
5.1.7 Write down the probability, as a decimal, of randomly selecting a month when the rail income for passenger transport was less than R200 000 000. (3)
5.1.8 A bar graph showing the monthly income for road transport for the last six months of the year, is drawn on ANSWER SHEET 1. On the same set of axes, draw another bar graph representing the monthly income for rail transport for the last six months of the year. (6)
5.2 The pie charts on ANNEXURE C show the different sources of income for households in the Western Cape and the Northern Cape in 2016.
Use ANNEXURE C to answer the questions that follow.
5.2.1 If the total number of households in the Western Cape was 2 768 000 during 2016, calculate the number of households that depend on grants as a source of income. (3)
5.2.2 Identify the THIRD HIGHEST source of income in the Western Cape. (2)
5.2.3 Calculate the difference between the number of households in the Western Cape and the Northern Cape that depended on business as a source of income for 2016. (3)
5.2.4 Determine the percentage (to TWO decimal places) of remittances in the Northern Cape if there were 532 000 households. (3) [35]
TOTAL: 150
ANSWER SHEET 1
QUESTION 5.1.8
CENTRE NUMBER:
EXAMINATION NUMBER:
VISUAL ARTS PAPER 1 GRADE 12 QUESTIONS - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
VISUAL ARTS
PAPER 1
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
INSTRUCTIONS AND INFORMATION
In this examination you must demonstrate the following skills:
- Using the correct art terminology
- Using and implementing visual analysis and critical thinking
- Writing and researching within a historical and cultural context
- Placing specific examples in a cultural, social, political and historical context
- Understanding distinctive creative styles
Read the following instructions before deciding which questions to answer.
- This question paper consists of EIGHT questions.
- Answer any FIVE questions for a total of 100 marks.
- Number the answers correctly according to the numbering system used in this question paper.
- Questions appear on the left-hand pages, with visual sources on the right-hand pages.
- Ensure that you refer to the visual sources reproduced in colour where required.
- Information discussed in one answer will NOT be credited if repeated in other answers. Cross-referencing of artworks is permissible.
- Name the artist(s) and title of each artwork you discuss in your answers. Underline the title of an artwork or the name of a building.
- Write in a clear, creative and structured manner, using full sentences and paragraphs according to the instructions of each question. The listing of facts/tables is NOT acceptable.
- Use the following guidelines for the length of your answers. Note the mark allocation.
- 6–8 marks: a minimum of ½–¾ page (paragraph)
- 10–14 marks: a minimum of 1–1½ page(s) (short essay)
- 20 marks: a minimum of 2 pages (essay)
- Write neatly and legibly.
QUESTIONS
ANSWER ANY FIVE QUESTIONS.
QUESTION 1: THE VOICE OF EMERGING ARTISTS
Read the poem below and answer the questions.
TRAVEL – Edna St Vincent Millay The railroad track is miles away, All night there isn't a train goes by, My heart is warm with friends I make, |
1.1 Visualise the poem above and select ONE phrase for EACH artwork (FIGURE 1a and FIGURE 1b). Motivate your choice by referring to the imagery, mood and atmosphere of the artwork. (6)
1.2 Compare the imagery in EACH artwork by referring to the focal point, composition and use of colour. (6)
1.3 Interpret the work of ONE artist you have studied, who comments on his/her daily experiences.
Include the following in your answer:
- Influences
- Formal art elements
- Media and technique
- Style
- Possible messages/meanings (8) [20]

FIGURE 1a: Lionel Davis, Train Ride, linocut, 2012.
FIGURE 1b: Ernst Ludwig Kirchner, Königstein Train Station, oil on canvas, 1916.
QUESTION 2: SOUTH AFRICAN ARTISTS INFLUENCED BY AFRICAN AND/OR INDIGENOUS ART FORMS
Pablo Picasso's artwork Les Demoiselles d'Avignon (FIGURE 2b) is regarded as one of the most important artworks of the 20th century and is the first international work to show an extensive African influence, whereas Irma Stern had first-hand experience of Africa due to her extensive travels around this continent. |
2.1 Both artists used the nude body. How do the composition and mood of FIGURE 2a and FIGURE 2b differ? (4)
2.2 Discuss the style with which, and the manner in which, the artists approached their subject matter. (4)
2.3 Discuss TWO artworks by different artists whose work shows evidence of an African/indigenous influence.
Use the following guidelines:
- Influences
- Style and technique
- African signs/symbolism
- Possible messages/meanings (12) [20]

FIGURE 2a: Irma Stern, The Hunt, oil on canvas, 1929.
FIGURE 2b: Pablo Picasso, Les Demoiselles d'Avignon, oil on canvas, 1907.
QUESTION 3: SOCIO-POLITICAL ART, INCLUDING RESISTANCE ART OF THE 1970s AND 1980s
Debris (rubbish/trash) and unwanted objects are used by both Penny Siopis and Fabrice Monteiro to comment strongly on sociopolitical issues in their artworks. |
3.1 Compare FIGURE 3a and FIGURE 3b.
Refer to the following guidelines:
- The placement/positioning and significance of the figure in EACH work
- The purpose of the drapery, or the lack thereof, in FIGURE 3a and FIGURE 3b
- The relevance of the title of EACH artwork
- What social issues has the artist addressed in FIGURE 3a and FIGURE 3b?
- Identify any object(s) that had been thrown away in FIGURE 3a and recycled in FIGURE 3b. Motivate your selection. (8)
3.2 Discuss TWO artworks you have studied which reflects resistance/ sociopolitical issues. (12) [20]
FIGURE 3a: Penny Siopis, Piling Wreckage upon Wreckage, oil on canvas, 1989. (Wreckage: the remains of something that has been badly damaged) 
FIGURE 3b: Fabrice Monteiro, The Prophecy Series, 'Untitled', photograph, 2014. (Prophecy: a prediction of what will happen in the future)
QUESTION 4: ART, CRAFT AND SPIRITUAL WORKS MAINLY FROM RURAL SOUTH AFRICA
Esther Mahlangu comes from a Ndebele background with a rich tradition of arts and crafts (FIGURE 4a). However, she has also become an acclaimed visual artist exhibiting all over the world using her familiar patterns and designs in a contemporary way. |
4.1 What would you see as the characteristics of the work of Esther Mahlangu? Consider the following:
- Art elements
- Materials and techniques
- Style and context
- The 'connection' between the past and the present in her artworks (10)
4.2 Discuss the work of TWO art, craft or spiritual artists who have used traditional methods to create their artworks.
Refer to the following in your discussion:
- Materials and techniques
- Possible influences
- Themes/subject matter
- Possible messages/meanings
- How these works have been influenced by the artists' cultures (10) [20]

FIGURE 4a: Esther Mahlangu in front of her Ndebele homestead, Mpumalanga, 2007. 
FIGURE 4b: Esther Mahlangu photographed at her 80th birthday, solo exhibition, Irma Stern Museum in Cape Town, South Africa, 2015.
QUESTION 5: MULTIMEDIA AND NEW MEDIA – ALTERNATIVE CONTEMPORARY AND POPULAR ART FORMS IN SOUTH AFRICA
The heritage of Surrealism is still being used by contemporary artists through their juxtaposition/contrast of different materials and unrelated images. |
5.1 Discuss the juxtaposition/contrast in FIGURES 5a to 5d by referring to the following:
- Symbolism and imagery
- Materials and textures
- Possible meaning and messages (10) .
5.2 Interpret any TWO artworks by different South African artists who use alternative/new media in search of ways to communicate issues. (10) [20]
FIGURE 5a: Max Ernst, Sacred Conversation, collage photomontage, 1921. 
FIGURE 5b: Edward Kienholz, John Doe, oil paint, metallic paint, resin, plaster and graphite on mannequin parts with wood, metal, plastic, paper, rubber and stroller, 1959. 
FIGURE 5c: Patrick Bongoy, Revenants III, mixed media, recycled rubber and hessian on a fiberglass cast, 2017. 
FIGURE 5d: Nicholas Hlobo, Ndiyafuna (I Am Looking for Something), fibreglass, rubber inner tube, ribbon, jeans, sneakers, lace and wood, 2006.
QUESTION 6: POST-1994 DEMOCRATIC IDENTITY IN SOUTH AFRICA
South Africa's democracy is based on a compromise between diverse political groups and the acceptance of our differences. – William Gumede |
6.1 Discuss how Witbooi in FIGURE 6a sees democracy in South Africa by referring to the following:
- Colour
- Influences
- Meaning and symbolism of the:
- Blindfolded figure
- Scales
- Tightrope
- Images in the background
- Different styles in the artwork
- Comment on the message the artist wanted to convey. (10)
6.2 Analyse the work of any TWO artists you have studied, whose works comment on the post-1994 identity of South Africa.
You may use the following ideas in your answer:
- Content of artworks and images
- Medium, style and techniques
- How the artists reflect their own questioning of the world and the spaces they occupy in South Africa, both physically and emotionally. (10) [20]

FIGURE 6a: Khaya Witbooi, Below the Law, stencilling and paint, 2014.
QUESTION 7: GENDER ISSUES: MASCULINITY AND FEMININITY
| Rather than following traditional gender roles, people interpret it in a personal way. As a result, gender roles and stereotyping are fading and pushing the boundaries of what it means to be feminine or masculine. |
Discuss the statement above and write an essay in which you comment on the way in which these gender boundaries are being questioned/pushed.
Refer to FIGURE 7a and FIGURE 7b, as well as any TWO artists who you have studied who comment on gender to substantiate your answer.
You may use the following as a guideline in your essay:
- Significance of colour
- Imagery and the possible interpretations thereof
- How the artists portray the attributes of masculinity and/or femininity:
- Comment on the word play of 'chic(k)' in the title of FIGURE 7a
- The significance of the clothing
- The mood created through facial expressions
- Relevance of the posture/gesture [20]

FIGURE 7a: Nicholas Allen, L'Hommage à Ingres: African Chic(k): Ms Tshegofatso Phage Seated, oil on canvas, 2013. 
FIGURE 7b: John Kirby, Self-portrait, oil on canvas, 1987.
QUESTION 8: ARCHITECTURE IN SOUTH AFRICA
Each new situation requires a new architecture. – Jean Nouvel |
8.1 Refer to the statement above and the images in FIGURES 8a and 8b and write a short essay in which you comment on how 'new architecture' is being used for shelter and accommodation in South Africa.
Respond to the following in your answer:
- The positive and negative aspects of using shipping containers as the answer to the housing crisis in South Africa
- Compare FIGURES 8a and 8b by discussing the aesthetic appeal of both buildings due to their modification.
- If you had the opportunity to live in a shipping container, what modifications would you suggest to make your home as functional as possible? (8)
8.2 Discuss the work of any architect you have studied whose work reflects a new approach to architecture that could satisfy the needs of a growing South African society.
Use the following guidelines to support your answer:
- Site and positioning
- Use of building materials
- Design and functionality
- Inspiration and influences
- How the architect has specifically addressed/considered the needs of the South African society

FIGURE 8a: Citiq Property Services (Pty) Ltd, Mill Junction, Johannesburg, Newtown, old mill and shipping containers, 2014. 
FIGURE 8b: Espace Mobile designed this retro-looking prefabricated house. It is located in the Austrian countryside, 2007.
TOTAL: 100
VISUAL ARTS PAPER 1 GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
VISUAL ARTS
PAPER 1
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before commencing marking:
- The marking guideline consists of EIGHT answers. Candidates had to answer any FIVE questions for a total of 100 marks.
- It is MOST IMPORTANT that allowance is made for the learners in many instances:
- Candidates must be given credit for providing their own opinions and ideas in their answers.
- Credit must also be given for lateral thinking.
- It is also important that arguments and statements are reasoned and qualified by reference to specific factors.
- Questions and subsections must be numbered clearly and correctly. Bullets usually act as guidelines to help structure learners' answers.
- Information and artworks discussed in one answer must not be credited if repeated in other answers but artworks may be cross-referenced.
- Where applicable, candidates must name the artist and title of each artwork mentioned. Only ONE mark is allocated for the correct artist and title of work.
- Where appropriate candidates may discuss both two-dimensional and three dimensional artworks in any question.
- Remember that many learners will be discussing these examples, never having seen them before. Markers therefore cannot expect factual, academic information. They should draw upon their own experiences, cultures and interpretations of the artworks, within the context of the question. Therefore markers need to be open-minded and flexible in the marking process.
GENERAL INFORMATION FOR MARKERS
- This marking guideline is to serve as a guideline for markers as well as a teaching tool. Therefore, the marking guideline for certain questions is in greater depth, so that the information may be used as learning material. Other parts of the marking guideline may merely be a suggested guideline.
- NOTE: Markers are encouraged to reward candidates for what they know, rather than penalise them for what they don't know.
- Although the information for the questions is given in point form, candidates must use an essay/paragraph format discussing their information in a holistic manner.
- Candidates must answer all the questions in FULL SENTENCES or PARAGRAPHS, according to the requirements of each question. Answers in point form cannot receive full marks. Full marks cannot be given if the title or artist is incorrect.
- Markers must refer to the Visual Arts CAPS document page 45 for a guideline to assess the levels of achievement.
Copyright reserved Please turn over
Visual Arts/P1 3 DBE/2018 SCE – Marking Guidelines
Assessing candidates' ability to analyse and respond to examples of visual culture
ACHIEVEMENT RATING CODE | TOPIC 3: VISUAL CULTURE STUDIES |
7 Outstanding 80–100% |
|
6 Meritorious 70–79% |
|
5 Substantial 60–69% |
|
4 Moderate 50–59% |
|
3 Adequate 40–49% |
|
2 Elementary 30–39% |
|
1 Not achieved 0–29% |
|
MEMORANDUM
CANDIDATE MUST ANSWER ANY FIVE QUESTIONS.
The following mark allocation must be adhered to when only ONE artwork/artist has been discussed instead of TWO.
- 6 marks (max 3)
- 8 marks (max 5)
- 10 marks (max 6)
- 12 marks (max 7)
- 14 marks (max 8)
- 20 marks (max 12)
QUESTION 1: THE VOICE OF EMERGING ARTISTS
The railroad track is miles away, Travel |
1.1 Candidates must visualise the poem above and select ONE phrase for each artwork that motivates their choice by referring to the imagery, mood and atmosphere of the artwork.
Candidates can select any phrase, however, the selection needs to be motivated
- FIGURE 1a: 'And the day is loud with voices speaking' OR 'My heart is warm with friends I make'.
The figures are represented in a standing position on a train. The black and white figures can be seen speaking and engaging with friends. - FIGURE 1 b: 'But I hear its whistle shrieking' OR 'Yet there isn't a train I wouldn't take, No matter where it's going'. The train is seen moving through the town/landscape with steam billowing from the chimney. The brightly coloured painting implies a happy and joyful mood. (6)
1.2 Compare the imagery in each artwork by referring to the focal point, composition and use of colour.
- FIGURE 1a: The figure with the handbag is the focal point; however, the candidate can mention that there is no definite focal point as the eye moves all over the picture plane. The composition is very claustrophobic, overcrowded and cramped by the overlapping of the figures in the middle ground. The artwork has a dramatic contrast of black and white with flat tones (no tonal effect in the colour). The figures are large in comparison to the train and dominate the composition.
- FIGURE 1b: The smoke and train form the focal point in the middle of the composition. The train is very small in relation to the rest of the composition. The artist uses bold, vibrant and non- representative (arbitrary) colour which can be seen in the blue roofs and red/pink grass.
One mark for a comparison/discussion. One mark of composition, one mark for discussion of colour and one mark for focal point per artwork. (6)
1.3 Candidates must interpret the work of ONE artist they have studied, who comments on their daily experiences.
They can include the following in their answer:
- Influences
- Formal art elements
- Media and technique
- Style
- Possible messages/meanings (8) [20]
QUESTION 2: SOUTH AFRICAN ARTISTS INFLUENCED BY AFRICAN AND/OR INDIGENOUS ART FORMS
Pablo Picasso's artwork Les Demoiselles d'Avignon (FIGURE 2b) is regarded as one of the most important artworks of the 20th century and is the first international work to show an extensive African influence, whereas Irma Stern had first-hand experience of Africa due to her extensive travels around this continent. |
2.1 Although both artists have made use of the nude body, how does the composition and mood differ between FIGURE 2a and FIGURE 2b?
- TEACHERS TOOL: Many of Stern's paintings of people are concerned primarily with the culture rather than the individual. The Hunt was a product of her journey to Swaziland and Natal during the 1920's. Picasso was influenced by African sculpture and the main point of Les Demoiselles d'Avignon was to challenge the viewer's normal assumptions.
- FIGURE 2a: The composition is very cramped. The smaller figures in the background create a feeling of depth in the painting, the perspective is distorted as there is little difference between foreground and background space.
The colours don't become less vibrant in the background and some figures in the background are out of proportion in relationship with each other on the particular plane of depth. The area of focus appears to be the three figures in the foreground. The figures are either naked or just wearing a loin cloth making them vulnerable. A feeling of activity is created by the use of angular lines often intersecting with each other. The use of bold colour gives a feeling of joy. The figures seem to be caught off guard which is evident in their facial expressions and body language. - FIGURE 2b: Les Demoiselles d'Avignon has a flatness and two dimensional approach with an absence of perspective. There is an uncomfortable mosaic of angular and overlapping fragments of five gigantic intrusive female nudes. The two central women are provocative as they stare expressionlessly at the viewer, aggressively flaunting their nudity. The overall impression of the painting is one of vibrant colours and pattern, but one does not feel any emotions in the subjects and they almost appear like bored models posing for a fashion shoot. (4)
2.2 Discuss the style and manner in which the artists have approached their subject matter.
- FIGURE 2a: Irma Stern used expressive brushstrokes, thick paint and bright colours to show her idealised, view of the world, rather than the suffering of Africa. The thick paint applied with a palette knife creates a sense of emotional intensity. She uses decorative curves, lines and S-shapes. She uses both arbitrary colour and real colour with loosely applied gestural marks.
The figures are stylised resembling the angularity found in African sculpture. - FIGURE 2b: Picasso uses flat, splintered imagery, together with patterns of light and dark (as opposed to rounded volumes), in order to create a sense of space and form. The figure (bottom right) is made up of a collage of different viewpoints of herself, while the others are depicted in a flattened geometric form. The painting's sharp, almost shard-like pictorial components imbue it with a disturbing sense of violence and sexual power. (4)
2.3 Candidates must discuss TWO artworks by different artists whose work shows evidence of an African/Indigenous influence.
They may use the following guidelines:
- Influences
- Style and technique
- African signs/symbolism
- Possible messages/meanings (12) [20]
QUESTION 3: SOCIO-POLITICAL ART, INCLUDING RESISTANCE ART OF THE 1970s AND 1980s
Debris (rubbish/trash) and unwanted objects are used by both Penny Siopis and Fabrice Monteiro to comment strongly on sociopolitical issues in their artworks. |
3.1 Candidates must compare FIGURE 3a with FIGURE 3b by referring to the following guidelines:
The placement/positioning and significance of the figure in each work
- FIGURE 3a: A mysterious female figure is positioned in the background of the landscape of an overabundant layered composition. Her figure is shrouded with white fabric in a classical Greek style. She holds the draping up in both her hands covering some of the objects in the composition. Perspective has been accentuated by the extremely small figure on a heap of debris and objects compacted into a waste-disposable site. The crowded objects raise questions about relationships of power as well as notions of self, identity and knowledge. The objects that Siopis uses have their own past that have once played a role in someone's life. Possessions embody people's personal memories and experiences but have also become a part of the wider social history and symbolism. Siopis uses random objects in her painting which comments on colonialism, gender and other discriminatory practices. She also comments on the misrepresentation of history by patriarchal Western society.
- FIGURE 3b: The large ghostly figure appears in a surreal composition of a jinn (an ancient supernatural genie) experiencing the ravages of modern man and placed as focal point on a dumping site. The figure is rising from the debris wearing a skirt made of waste and plastic bags. Her headpiece and jewellery have also been made from recycled materials. The figure is moving towards a vast open landscape. Grey smoke is seen emerging from the dump site creating an eerie atmosphere.
The purpose of the drapery/lack thereof in FIGURE 3a and 3b
She is holding a large piece of drapery/fabric in both hands which cascades towards the bottom of the composition. The fabric is used as a metaphor to reveal or conceal the compacted and heaped rubbish dump of objects being thrown away by society.
- The relevance of the titles of each artwork FIGURE 3a: 'Piling wreckage upon wreckage' The title indicates that the random objects are seen as wreckage of our society and are piled up. Our attention is focused on the idea that our society is built up on the debris of our past history. It could also refer to the misrepresentation of history by Western patriarchal society.
FIGURE 3b: 'The prophecy'
The title refers to the figure as a prophet. The prophet's function will be to deliver a message to the people that if they don't look after the planet and their surroundings there will be nothing left for the future generations.
- What social issues has the artist addressed in FIGURE 3b and 3b? Fabrice Monteiro wanted to create awareness about the risk of modern man's pollution in Africa, highlighting the negative use of plastic bags and other serious environmental problems.
- Identify any object/s that have been thrown away in FIGURE 3a and recycled in FIGURE 3b. Motivate your selection.
Candidates can mention any object seen in FIGURE 3a such as vase, picture frame, paper scroll, flowers, Venus statuette, candelabra, plastic bags, bottles etc. We live in a consumer society where items are discarded easily and new things bought just to continue the cycle. (8)
3.2 Candidates must discuss TWO artworks they have studied, which reflects resistance/socio- political issues. (12) [20]
QUESTION 4: ART, CRAFT AND SPIRITUAL WORKS MAINLY FROM RURAL SOUTH AFRICA
Esther Mahlangu comes from a Ndebele background with a rich tradition of arts and crafts (FIGURE 4a). She has, however, also become an acclaimed visual artist exhibiting all over the world using her familiar patterns and designs in a contemporary way. |
4.1 By discussing FIGURE 4a and FIGURE 4b, candidates must discuss the characteristics of Esther Mahlangu by referring to the following:
- Art elements
FIGURE 4a: Vertical, horizontal and diagonal lines are used in her artworks. She creates brightly coloured (red, blue, yellow, green and purple) geometric shapes which are outlined in black. She also makes use of white in the background of her works. The repetition of the lines, shapes and colours create a decorative pattern. The blankets that the women are wearing are divided up into bands of red, brown, yellow and blue colour. They are also wearing brightly coloured jewellery around their necks and legs which are made from glass beads.
FIGURE 4b: Vertical, horizontal and diagonal lines are seen in her artwork on the walls of the gallery and interior of the car. She creates brightly coloured geometric shapes that cover the surface of the artwork or specific part of the car's interior. Her shapes are outlined in black and/or white lines. She uses bright colours e.g. yellow, blue, green and pink.
- Materials and techniques
FIGURE 4a and FIGURE 4b: Mahlangu applies paint to the plastered surface of the wall of the house. Black lines are used to outline the different brightly coloured geometrical shapes. The traditional beadwork is made by hand stringing different colours of glass beads in different patterns. The vessel is made from a calabash.
- Style and context
FIGURE 4a: Mahlangu is influenced by her Ndebele traditional culture which she inherited from her mother and grandmother. The houses have been painted in the traditional Ndebele geometric design. The figures wear traditional jewellery made from beads and copper rings. The vessels used for storage of water etc. are known as calabashes and these are also used and transformed into works of art and functional everyday items.
FIGURE 4b: Mhlangu honours her traditional Ndebele culture by still wearing a traditional Ndebele outfit although she is standing in a contemporary art gallery. She wears a traditional brightly coloured Ndebele blanket with a headpiece and jewellery around her neck and ankles made from coloured glass and brass. Brightly coloured geometric shapes and patterns are painted on the interior panels of the 7 series BMW car. Paintings/artworks with the same designs can be seen hanging on the gallery walls.
- The candidate's understanding of what is meant by the 'connection' between the past and the present in her artworks Her traditional decorative painting has been reused and applied to many different surfaces e.g. clothing, shoes/sneakers, skateboards, walls, glass bottles and cars.
FIGURE 4a: Mahlangu is photographed in front of her traditional Ndebele homestead wearing an Ndebele outfit. She pours water from a calabash. The Ndebele clothing and the use of the calabash is evident of her past/traditions and she still has a connection with the past as she still uses these items in a modern society.
FIGURE 4b: Mahlangu is photographed in a contemporary art gallery where her traditional artworks are exhibited on the walls and on the interior panels of the BMW. The 'connection' here is made with the present. She communicates and informs us on the practices and importance of her culture and the preservation thereof for future generations. (10)
4.2 Candidates must discuss the work of TWO art, craft or spiritual artists who have used traditional methods to create their artworks. They can refer to the following in their discussion:
- Materials and techniques
- Possible influences
- Themes/subject matter
- Possible messages/meanings
- How these works have been influenced by the artist's culture (10) [20]
QUESTION 5: MULTIMEDIA AND NEW MEDIA – ALTERNATIVE CONTEMPORARY AND POPULAR ART FORMS IN SOUTH AFRICA
The heritage of Surrealism is still being used by contemporary artists through their juxtaposition/contrast of different materials and unrelated images. |
5.1 Candidates must discuss the juxtaposition/contrast in FIGURES 5a-5d by referring to the following:
- Symbolism and imagery:
FIGURE 5a: Two female figures are seen facing the viewer in an enclosed space. The dressed figure on the right is headless while the posing central figure is nude. The central figure, which is the focal point, is divided into different juxtaposed, unrelated parts. Some body parts appear to be frayed or x- rayed exposing the nerves and bone. The body parts give the idea of drawings from a medical/anatomical journal. The oval disk around the legs, mathematical images in the abdomen and mechanical object placed on the left side of the face refer to technology, industrialisation or the horrors of WW1. Two birds/doves are superimposed over the two figures which could symbolise purity, spirituality or even have a religious connotation. The image becomes dreamlike/fantasy like.
- Materials and textures:
FIGURE 5a: The combination and juxtapositioning of different mechanical, industrial and anatomical parts is distressing and creates a mood of discomfort. The use of anatomical/x-rayed images makes the viewer uncomfortable.
FIGURE 5b: The artist created a 3- dimensional sculpture using unrelated/ discarded found objects. The mannequin's head and torso have been splattered with paint and placed within a baby pram creating a shocking and haunting effect. The chest cavity of the torso has been hollowed out and a cross has been placed where the heart should be The mannequin is propped up against a wooden log.
FIGURE 5c: Revenants III represents a pregnant figure with a head emerging from a hessian sack. The hessian sack is a coarsely woven fabric and is worn as a garment. The sack, disused rubber and mannequin, imply that people are treated like trash. It de-humanises the human form, and creates a disturbing work. The rubber flaps extruding from her frame indicate that she is falling apart or changing shape. Pieces of rubber protrude from the legs and arms of the mannequin. It seems like spikes have been driven through the skin. It invites the viewer to touch the textures as if to soothe the skin. The rubber chain around her waist extends to the floor also create a tactile texture. It invites the viewer to feel and identify the material. Hessian, a coarse woven fabric, is wrapped around the head of the female figure almost suffocating her. Smooth gold antennae are seen protruding from her ears
FIGURE 5d: This 3-dimensional sculpture represents a figure bending over with his/her upper torso concealed in a large bag as if he/she is looking for something. It almost takes on the resemblance of a caterpillar. The figure is made from rubber tubing as well as his underwear. The figure which is made predominately from black rubber tubing wears a pair of blue jeans halfway down his buttocks with his boxers revealed- making reference to certain fashion trends.
- Possible meaning and messages:
FIGURE 5a: The juxtaposition of different images to create a fantasy, dreamlike Surrealist artwork.
FIGURE 5b: A powerful and haunting image that reminds us of death.
FIGURE 5c: The human form appears to be de-humanised. The hessian fabric is wrapped around the head almost suffocating the sculpture. The rubber chain is also an indication of her being contained and imprisoned. The chain could represent an umbilical cord. The texturised rubber pieces protruding from her legs and arms could refer to her being tortured and distressed.
FIGURE 5d: The artists' interpretation of the artwork is that of a creature swallowing a person. The idea of searching for or concealing one's identity is created. The idea of the known and unknown, being ejected or consumed, inside-outside, comfort, shelter, contrast, perfection, sacred space, pleasure, fantasy, duality are created. The sculpture makes the viewer feel uncomfortable and claustrophobic. The meaning is ambiguous and might refer to sextuality and cultural practices. (10)
5.2 Candidates must interpret any TWO artworks by different South African artist/s who use alternative/new media in search of ways of communicating pressing issues. (10) [20]
QUESTION 6: POST-1994 DEMOCRATIC IDENTITY IN SOUTH AFRICA
South Africa's democracy is based on a compromise between diverse political groups and the acceptance of our differences. – William Gumede |
6.1 Candidates must discuss how Witbooi sees South Africa's democracy by referring to the following:
- Colour: The monochromatic greys and blacks of the figure, create an eerie mood. It can also imply the classical heritage and the symbolism of Lady Justice. The grey tones of the figure contrast sharply with the vibrant pink of the graffiti in the background. The grey and khaki squares forming the background of the graffiti create a rhythmic pattern. Black is used in the typography/text of the graffiti and the masked figures.
- Influences: The artist could be influenced by collage-style paintings/artworks, graffiti, pop art, and hip-hop culture.
- Meaning and symbolism of:
- The blindfolded figure: The blindfolded female figure (representing Lady Justice) walks on a tight rope attempting to balance the scales she is carrying. Being blindfolded makes it dangerous to walk on a suspended tight rope. She could represent the strength of South African women walking blindly into a new democracy. She is fully clothes and her dress is made of soft fabric, and draped in a classical Roman fashion. The blindfolded woman represents all men and women of society who were handcuffed by a discriminating law. A shackle on her right wrist could symbolise that she has broken free, being above the law but still on a tight rope of uncertainties.
TEACHING TOOL: The blindfold represents impartiality, the ideal that justice should be applied without regard to wealth, power, or other status. The Roman inspired garment symbolises the status of the philosophical attitude that embodies justice.
- The scales: The figure carrying the scales is a metaphor of the men and women in South Africa trying to balance knowledge and ignorance in the social and racial hierarchies of contemporary South Africa. The scales could also symbolise the balance between good and bad.
- The tight rope: The Justice system in South Africa is sometimes seen as unfair and unjust. The blindfolded figure that walks on the rope represents the people of South Africa who are trying to create a balance in their lives.
- Images in the background: There is a mosaic of graffiti images in the background of the artwork. Bushman images, forgotten people, a naval officer, a hand grenade representing violence, clenched fists and a repetitive mask of a Star Wars character is visible in the background. They could represent the diversity of society. There are definite spray-painted words all over the artwork.
- Different styles in the artwork: The female figure is portrayed in a naturalistic manner; however, it has stylistic characteristics like simplification and pop/cartoon like imagery. Stencilling has been used in the background.
TEACHING TOOL: Witbooi is renowned for his 'Afro-pop' collage style paintings. Witbooi lists Picasso and Asha Zero as his influences. He coined the word 'pap-art' – being 'pap' the traditional poor staple food in Southern Africa – to define his personal approach to contemporary art as a self-taught artist.
- Comment on the message the artist wanted to convey:
Lady Justice is an allegorical personification of the moral force in judicial systems The message could represent women fighting for equality in South Africa. The blindfolded female figure represents women in today's society who are handcuffed by the law/man. She is portrayed breaking free from discrimination be it the law or prejudice/bias/stereotyping. She is blindfolded while trying to find her voice in society and is expected to abide by the law. She is balancing all the roles that are expected from women in today's society. It can also represent the balance between good and evil. (10)
6.2 Candidates must analyse the work of any TWO artists they have studied whose works comment on the post 1994 identity of South Africa.
They may use the following ideas in their answer:
- Content of artworks and images
- Medium, style and techniques
- How the artists reflect their own questioning of the world and the spaces they occupy in South Africa, both physically and emotionally. (10) [20]
QUESTION 7: GENDER ISSUES: MASCULINITY AND FEMININITY
Rather than following traditional gender roles, people interpret it in a personal way. As a result, gender roles and stereotyping are fading and pushing the boundaries of what it means to be feminine or masculine. |
7.1 Candidates must discuss the above statement and write an essay in which you comment on the manner in which these gender boundaries are being questioned/pushed. You must refer to FIGURE 7a and b as well as any TWO artists they have studied, who comment on gender. Answers must be Substantiated.
They may use the following as a guideline in their essay:
- Significance of colour :
FIGURE 7a: Contrasting colours have been used in the clothing of the female figure e.g. oranges and turquoise. The burnt orange/brown panels of interior and her dress are very similar in terms of colour. The colour of turquoise ribbons is repeated in the vase on the left hand side of the painting. The white blouse becomes the focal point of the painting. The figure is sitting on a pink coloured cushion which represents and symbolises femininity
FIGURE 7b: The intense dark background (chiaroscuro) contrasts with the light skin of the figure. The figure is portrayed in ladies garment however the colour blue traditionally refers to masculinity. A red rose is attached to the garment, usually representative or symbolic of love and virginity.
- Imagery and the possible interpretations thereof:
FIGURE 7a: It is a portrait of a seated lady dressed in a white top and wide red patterned skirt. Her reflection indicates that she has a cell phone in her left hand; however, the seated figure is not painted with a cell-phone but rather a broom in the opposite hand. There is a contrast between the past and present technology. The use of mirrors creates an illusion of space and perspective. She is also adorned with jewellery that is a combination of both modern and traditional. Her hair is neatly tied back with fabric/ ribbon. In her left hand she holds a small handmade grass broom symbolic of domestication. A woven traditional basket is placed next to the vase which is usually used as a storage item. A slaughtered chicken is seen hanging in the background of painting which still needs to be cooked and served. She is represented in an ornate interior with gilded frames and a decorated mantelpiece which suggests wealth. The porcelain vase on the left has turquoise bands and images of cattle. Cattle, which represent wealth, are often used as lobola payment in African wedding ceremonies. The portrait can be compared to those portraits painted by the Neo Classical artists.
FIGURE 7b: It is a self-portrait by the artist who is dressed in ladies' slip/undergarment. He has a tattoo on his left arm, which looks like a bird symbolic of freedom. Tattooed men are often regarded as being masculine, brave and daring. The red rose which is attached to the blue garment symbolising virginity or femininity. The gesture of the figure is very similar to that of Leonardo Da Vinci's ' St. John the Baptist'.
- How the artists portray the attributes of masculinity and/or femininity
- Comment on the play of word 'chic(k)' in the title of FIGURE 7a:
In the title the 'k' in Chick is inverted and can refer to the chicken in the background that still has to be cooked and served. 'Chick' is a word commonly used by males to address women. She looks 'chic' meaning that she is smartly dressed with an elegant flair. Although women can be chic, they are still expected to complete their daily domestic tasks.
- Significance of the clothing:
FIGURE 7a: The female figure is dressed in a white blouse and red/burnt orange skirt. She has turquoise ribbons draped around her which contributes to her femininity. She wears a bangle on each wrist and a ring on her left hand. The jewellery contributes to making her feminine.
FIGURE 7b: Although this man wears ladies' underwear he is still portrayed as masculine. It is as if the artist wants to emphasise the fact that clothing does not determine gender. The shoulder strap on the left shoulder is falling off symbolising sensuality. The rose is also a middle aged symbol of virginity. It seems as if he is posing for a photo or performing on stage.
- Mood created through facial expressions:
FIGURE 7a: The female figure is looking at the viewer seeming to pose for a photograph. She is comfortable and looks as if she is used to being the lady of the house. A soft, feminine mood is created by her eye contact with the viewer.
FIGURE 7b: The male figure has a slight drooping mouth which makes him look self- conscious. A sad and melancholy mood is created. The subject matter is very similar to Picasso's paintings of circus people.
- Relevance of the posture/gesture:
FIGURE 7a: The figure has a very relaxed, yet sensual pose. Her right hand frames her face as if she is posing for a photograph.
FIGURE 7b: The figure is in a standing position and his hands show/portray feminine gestures. [20]
QUESTION 8: ARCHITECTURE IN SOUTH AFRICA
Each new situation requires a new architecture. – Jean Nouvel |
8.1 By referring to the above statement and the images in FIGURE 8a and 8b, candidates must write a short essay in which they comment on how 'new architecture' is being used for shelter and accommodation in South Africa.
They must respond to the following in their answer:
- The positive and negative aspects of using shipping containers as the answer to the South African housing crisis.
Positive aspects: In South Africa, the housing crisis can be solved by using strong, safe, shipping containers in townships/rural areas. Squatter camps can be upgraded by replacing the unsustainable cardboard and plastic with a stronger structure like a steel container. On site construction is eliminated as these containers can be modified and the interior be completed beforehand. The containers are stable and solid and can be piled on top of one another. Due to their strength containers provide safe housing solutions.
Negative aspects: The steel containers are very heavy and therefore difficult to transport. The modifications of the units are also expensive. Once the container has been delivered it cannot be dismantled.
- Compare FIGURE 8a and 8b by discussing the aesthetic appeal of both buildings due to their modification.
FIGURE 8a: The building in FIGURE 8a was created by modifying shipping containers and stacking them on an old unused mill. The containers are equipped with windows and extended balconies. The roof is accessible and a circular structure can be seen which could be used as extra living space.
Painting them in various colours create a Neo- Modernistic feel. Suspended balconies form a contrast to the flat façade and create extra space. The round cement mills contrast sharply with the angular, brightly coloured shipping containers.
FIGURE 8b: It is a minimalistic house propped up on grey concrete beams. The building has a free façade, ribbon windows, an extended balcony/veranda. The panels of glass allow light to enter the building as well as the integration of the interior and exterior. The building has a flat roof.
- If you had the opportunity to live in a shipping container what modifications would you suggest in making your home as functional as possible?
Shipping containers are versatile and can be modified to suit all individual preferences. The containers can be painted in numerous colours or left as is. A roof garden can be added to the top levels for growing greeneries as well as solar panels to generate electricity. Units can be added on when needed. For safety, smaller windows can be used. Alternatively, large glass walls can replace a steel wall to integrate the interior and exterior.
The candidate's own response will be considered. (8)
8.2 Candidates must discuss the work of any architect they have studied whose work reflects a new approach to architecture that could satisfy the needs of an ever growing South African society.
They may use the following guidelines to support their answer:
- Site and positioning
- Use of building materials
- Design and functionality
- Inspiration and influences
- How the architect has specifically addressed/considered the needs of South African society. (12) [20]
TOTAL: 100
MECHANICAL TECHNOLOGY GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2018
MECHANICAL TECHNOLOGY
GRADE 12
AMENDED SENIOR CERTIFICATE EXAMS
PAST PAPERS AND MEMOS
MAY/JUNE 2018
MEMORANDUM
QUESTION 1: MULTIPLE-CHOICE
1.1 A ✔ (1)
1.2 D ✔ (1)
1.3 B ✔ (1)
1.4 A ✔ (1)
1.5 A ✔ (1)
1.6 B ✔ (1)
1.7 D ✔ (1)
1.8 A ✔ (1)
1.9 B ✔ (1)
1.10 D ✔ (1)
1.11 D ✔ (1)
1.12 B ✔ (1)
1.13 C ✔ (1)
1.14 A ✔ (1)
1.15 A ✔ (1)
1.16 C ✔ (1)
1.17 D ✔ (1)
1.18 D ✔ (1)
1.19 C ✔ (1)
1.20 A ✔ (1) [20]
QUESTION 2: SAFETY
2.1 Angle grinder safety attire:
- Wear eye protection ✔
- Wear ear plugs or muffs ✔
- Wear safety boots ✔
- Wear overalls/leather apron ✔
- Wear safety gloves ✔
(Any 2 x 1) (2)
2.2 Hydraulic press safety:
- The prescribed pressure must not be exceeded ✔
- Ensure the pressure gauge is in a working order ✔
- The platform on which the work piece rests must be rigid and square with the cylinder of the press ✔
- Only prescribed equipment must be used ✔
- Check that the securing pins for the platform are properly in place ✔
- Check on hydraulic pipes for leaks and/or oil on the floor ✔
- Bearing need to be placed in a suitable jig ✔
- The apparatus should be checked regularly if all bolts and nuts are tightened ✔
- The level of the hydraulic fluid in the reservoir should be checked regularly. If fluid has to be added frequently, it is an indication that there may be an internal leak. ✔
- Regularly inspect the apparatus for rigidity and tighten all nuts and bolts. ✔
- Pins and/or other equipment that keep the platform at a desired height on the frame must be inspected regularly for damage. ✔
- When the apparatus is equipped with cables to alter the working height of the platform, the cable and pulleys must be inspected for damage and lubricated with grease.
✔ (Any 3 x 1) (3)
2.3 Arc welding helmet/-shield:
- To protect your skin and eyes against the dangerous ultra-violet Rays and sparks ✔
- To protect your face when chipping the slag ✔ (1)
2.4 Milling Machine:
- Always clamp work pieces and clamping devices properly. ✔
- Know where the ON/OFF switch is located. ✔
- Make sure that all guards are in place. ✔
- Wear all necessary safety equipment. ✔
- Do not use machine without permission. ✔
- Make sure that the machine is in working order. ✔
- Make sure the area around the machine is free of oil or scrap metal. ✔
- Do not wear loose clothing ✔
- Keep any cleaning material such as waste and rags away from rotating parts ✔
- Make sure that all guards are in place. ✔
- Spanners or keys must never be left on rotary parts. ✔
- Select the correct tool for the job. ✔
- Do not lean on a machine at any time. ✔
- Give attention to cutting-fluid control before switching the machine on. ✔
(Any 2 x 1) (2)
2.5 Safety aspect:
- Switch the machine off. ✔ (1)
2.6 Spring compressor safety :
- Make sure that the jaws/clamp of the spring compressor will not slip.✔
- Make sure that the compressor bolts are strong enough. ✔
- Do not over load the compressor. ✔
- Be careful when compressing or releasing the coil spring. ✔
- Do not use a hammer to remove the coil spring from the compressor. ✔
- Do not use wire to tie spring✔
(Any 1 x 1) (1) [10]
QUESTION 3: TOOLS AND EQUIPMENT
3.1 Testers
3.1.1
- The purpose of the fuel pressure tester is to test the fuel operating pressure in the system ✔ and fuel pressure in the fuel line that runs to the direct injection system. ✔ (2)
3.1.2 The purpose of the torsion tester is to investigate the relationship between torque ✔ applied to material and the influence of material length on torsional deflection. ✔ (2)
3.1.3 A cylinder leakage tester is used to check whether gases/compressed air leak ✔ from the cylinder in the engine during compression stroke. ✔ (2)
3.2 Reasons to perform a cylinder leakage test:
- To determine the percentage of leaking ✔
- To identify the location of the leak ✔ (2)
3.3 MIGS/MAGS – Welding
3.3.1 Advantages of MIGS/MAGS welding :
- Less cleaning of weld required ✔
- Thinner material can be welded ✔
- Less skill needed ✔
- Continuous welding is possible ✔
- Less defects occur ✔
- Can weld in any position ✔
- Causes less deformation ✔
- Gives a better finish ✔
- Faster than arc welding ✔
(Any 2 x 1) (2)
3.3.2 MIGS/MAGS gases:
- Argon ✔
- Helium ✔
- Teral ✔
- CO2 (Carbon di-oxide) ✔
(Any 2 x 1) (2) [12]
QUESTION 4: MATERIALS
4.1 Higher critical temperature:
- This is the highest temperature to which steel can be heated to obtain maximum hardness. ✔✔ (2)
4.2 Iron-carbon Structures
4.2.1
- Soft ✔
- Coarse grain structure ✔
- Non-magnetic ✔
(Any 2 x 1)(2)
4.2.2
- A- Ferrite + Pearlite ✔
- B. Ferrite ✔
- C. Ferrite + Austenite ✔
- D. Austenite ✔
- E. Austenite + Cementite ✔
- F. Pearlite + Cementite ✔
- G. 100% Pearlite ✔ (7)
4.2.3 900 °C ✔✔ OR 900-920 °C ✔✔ (2) [13]
QUESTION 5: TERMONOLOGY
5.1 Parallel key
5.1.1
- Width = D
4
= 84
4
= 21 mm ✔ ✔ (2)
5.1.2
- Thickness = D
6
= 84
6
= 14 mm ✔ ✔ (2)
5.1.3
- Length = D × 1.5
= 84 × 1.5
= 126 mm ✔ (2)
5.2 Indexing:
- Indexing = 40
n
= 40 ÷ 2
106 2
= 20 ✔
53
No full turns and 20 holes onthe 53 -hole circle (3)
5.3 Depth of the screw thread:
- Height = 0.866P
= 0.866 × 2 ✔
= 1.73 mm ✔ (2)
5.4 Spur gear
5.4.1 Addendum
- = m
= 3 mm ✔ (1)
5.4.2 Dedendum
- = 1,157 m or 1,25 m
= 1,157 x 3 ✔ 1,25 x 3 ✔
= 3,47 mm ✔ 3,75 mm ✔ (2)
5.4.3 Clearance
- = 0,157 m or 0,25m
= 0,157 x 3 ✔ 0,25 x 3 ✔
= 0,47 mm ✔ 0,75 mm ✔ (2)
5.4.4
- Module = PCD
T
PCD = m × T
= 3 × 48
= 144 mm ✔ (2)
5.4.5
- OD = PCD + 2m
= 144 + 2(3)
= 144 + 6 ✔
= 150 mm ✔ (2)
5.4.6 Cutting depth
- = 2,157 m or 2,25 m
= 2,157 x 3 ✔ 2,25 x 3 ✔
= 6,47 mm ✔ 6,75 mm ✔ (2)
5.4.7 Circular pitch
- = m x π
= 3 x π ✔
= 9,43 mm ✔ or 9,42 mm ✔ (2)
5.5 Type of key shown in FIGURE 5.5
- Parallel key ✔✔ OR Pratt and Whitney key✔✔ OR Feather key✔✔
(Any 1 x 2) (2)
5.6 Type of milling process shown in FIGURE 5.6
- Straddle milling ✔✔ (2)
5.7 Type of engineering equipment shown in FIGURE 5.7
- Milling machine ✔✔ (universal or vertical or horizontal milling machine) (2) [30]
QUESTION 6: JOINING METHODS
6.1 Causes of welding defects
6.1.1 Porosity:
- Atmospheric contamination ✔
- Surface contamination ✔
- Dirty or wet electrodes with arc welding ✔
- Rusted wire with MIGS/MAGS ✔
- Lack of shielding gas ✔
(Any 1 x 1) (1)
6.1.2 Undercutting:
- Improper settings of equipment ✔
- Welding speed to fast ✔
- Current too high ✔
(Any 1 x 1) (1)
6.1.3 Slag inclusion:
- Current to low ✔
- Included angle too narrow ✔
- Rapid chilling ✔
- High viscosity of molten metal ✔
- The previous weld slag has not been removed ✔
- Defective consumables/wet welding rods ✔
- Inadequate shielding gas flow ✔
- Welder’s negligence ✔
- Joint contamination ✔
(Any 1 x 1) (1)
6.2 Destructive tests:
- Nick break test ✔
- Bend test ✔
- Machinability test ✔
- Tensile test ✔
(Any 3 x 1) (3)
6.3 Dye penetration test:
- Clean the weld that needs to be tested. ✔
- Spray dye onto the surface and leave to penetrate. ✔
- Excess dye is cleaned away with a cleaning agent.✔
- Allow surface to dry. ✔
- Spray a developer onto the surface to bring out the dye trapped in the crack. ✔
- The dye will show all the surface defects. ✔ (6)
6.4 Inert gas:
- Stabilizes the arc. ✔
- Prevent atmospheric contamination. ✔
- Minimises weld spatter. ✔
- Prevent porosity. ✔
- Ensure proper fusion. ✔
- Shield weld pool from atmosphere ✔
(Any 3 x 1) (3)
6.5 MIGS/MAGS welding:
- Amount of penetration and fusion ✔
- Rate of weld wire feed ✔
- Rate of weld wire burning ✔
- The way the weld metal flows ✔
- The sound of the welding process ✔
(Any 3 x 1) (3)
6.6 MIGS/MAGS welding process:
- Parent metal ✔/Work piece ✔
- Weld pool ✔
- Electrode wire ✔
- Gas shroud ✔
- Contact tube ✔
- Shielding gas ✔
- Earth cable ✔/terminal/ground wire/skelm ✔ (7) [25]
QUESTION 7: FORCES
7.1 Resultant: 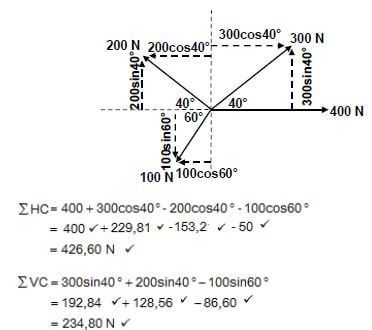
OR
Horizontal components | Magnitudes | Vertical components | Magnitudes |
300NCos40° | 229,81 N ✔ | 300NSin40° | 192,84 N ✔ |
-200NCos40° | -153,21 N✔ | 200NSin40° | 128,56 N✔ |
400 N | 400 N ✔ | 0 N | 0 N |
-100NCos60° | -50 N ✔ | -100Sin60° | -86,60 N ✔ |
TOTAL | 426,6 N ✔ | TOTAL | 234,80 N ✔ |
NB: 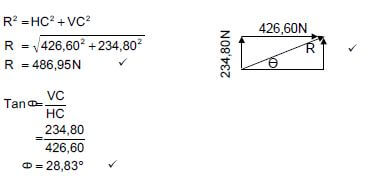
Resultant = 486,95 N 28,83° North from East ✔ (13)
7.2 Stress and Strain
7.2.1 Stress:
 (5)
(5)
7.2.2 Strain:
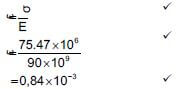 (3)
(3)
7.2.3 Change in length:
 (3)
(3)
7.3 Moments 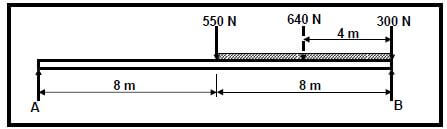
Calculate A. Moments about B:
- ∑RHM =∑ LHM
(A × 16) = (550 × 8) + (640 × 4) + (300 × 0)
16A = 6960
16 16
A = 435 N
Calculate B. Moments about A:
- ∑LHM =∑ RHM
(B × 16) = (300 × 16) + (640 × 12) + (550 × 8)
16B = 16880
16 16
B = 1055 N ✔ (6) [30]
QUESTION 8: MAINTENANCE
8.1 Viscosity:
- Due to higher pressure ✔between surfaces, it must ensure that the gears are well coated with oil and do not lose the lubrication barrier between them. ✔ (2)
8.2 Reason using SAE 20W50:
- This is to ensure that the oil is able to satisfy the operational requirements over a range of temperatures from start-up to running temperature. ✔✔ (2)
8.3 Pour point:
- Pour point is the lowest temperature at which a liquid remains pourable. ✔ (1)
8.4 Properties of grease:
- It must be water resistant/it must not mix with water. ✔
- Low freezing point. ✔
- Prevents rust/corrosion. ✔
- Good for load pressures. ✔
- High melting point. ✔
(Any 2 x 1) (2)
8.5 Maintain cutting fluid:
- Avoid contamination of the cutting fluid by draining and regularly replacing it. ✔
- Remove metal cutting from the machine's splash tray. ✔
- Ensure that the sump is topped up from time to time. ✔
- Check that there is sufficient flow of cutting fluid to the cutting tool. ✔
(Any 3 x 1) (3)
8.6 Viscosity of engine oil:
- The oil will not stay between the surfaces in contact, it will just flow through. ✔
- The oil will not have enough time to carry away the heat generated by the friction of the moving parts. ✔
- Increase of wear and tear will occur ✔ (2)
8.7 Reason for skimming flywheel:
- To obtain efficient contact between the flywheel and clutch✔
- To remove grooves caused by wear✔
- To remove hot spots on flywheel. ✔ (3) [15]
QUESTION 9: SYSTEM AND CONTROLS
9.1 Gear drives
9.1.1 Rotation frequency of the output shaft:
- ND = TA × TC
NA TB × TD
ND = TA ×TC × NA
TB × TD
NA = 40 × 30 × 1440
60 × 80
=360 r/min (3)
9.1.2 Velocity Ratio: N VR
- VR = NINPUT
NOUTPUT
= 1440
360
= 4:1 (2)
9.2 Belt Drives
9.2.1 Rotation frequency of the driver pulley: 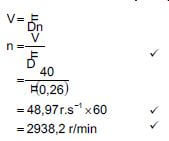 (3)
(3)
9.2.2 Power transmitted:
- T1 = 2,5
T2
T1 = 2,5 × T2
= 2,5 × 140
= 350 N
P = (T1 - T2)V
P = (350 - 140)40
= 8400 Watt
= 8, 4 kW (5)
9.3 Hydraulics
9.3.1 Fluid pressure: 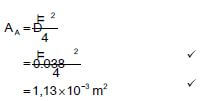
PA × F
AA
= 250 PA
1,13 × 10-3
= 221,24 × 10-3 Pa
= 221,24 kPa (4)
9.3.2 Distance moved by piston B in 10 strokes: 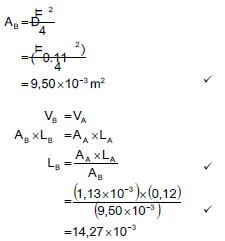
Movement = 14,27mm × 10 strokes
= 142,7 mm (4)
9.4 Advantage of ABS:
- ABS system prevents wheels from locking and skidding ✔ when braking during extreme conditions. ✔ (2)
9.5 Air Bags:
- It is seen as a passive safety feature because the driver and passengers in the vehicle do not need to activate the air bags ✔ or do anything to be protected by air bags. ✔ (2) [25]
QUESTION 10: TURBINES
10.1 Reaction Turbine:
- Francis ✔
- Kaplan ✔
- Tyson ✔
- Gorlov ✔
(Any 2 x 1) (2)
10.2 Impulse Turbine:
- Impulse turbine changes the velocity of a water jet. ✔
- The jet pushes on the turbine's curved blades which changes the direction of the flow. ✔
- The resulting change in momentum (impulse) causes a force on the turbine blades. ✔
- Since the turbine is spinning the force acts through a distance and the diverted water flow is left with diminished energy. ✔
- Prior to hitting the turbine blades the water's pressure is converted to kinetic energy by a nozzle and focused on the turbine. ✔
- No pressure change occurs at the turbine blades. ✔ (6)
10.3 Control of speed of steam turbine:
- To prevent ✔ the turbine rotor to reach an uncontrollable speed. ✔ (2)
10.4 Advantages of gas turbine:
- Smooth running due to absence of reciprocating parts. ✔
- Few moving parts causes less friction and wear. ✔
- Easy starting. ✔
- Can use wide range of fuels. ✔
- No water cooling system required. ✔
- Non-poisonous gasses emitted. ✔
- Require little routine maintenance. ✔
- Higher power-to-weight ratio, compared to reciprocating engines. ✔
- Moves in one direction only, with far less vibration than a reciprocating engine. ✔
- Low operating pressures. ✔
- High operation speeds. ✔
- Low lubricating oil cost and consumption. ✔
(Any 3 x 1) (3)
10.5 Waste gate:
- A waste gate diverts exhaust gases away from the turbine wheel. ✔
- It regulates the turbine speed to obtain maximum boost pressure. ✔ (2)
10.6 High altitude:
- Performance will decrease ✔ because of less oxygen at higher altitude levels. ✔
- Decreases volumetric efficiency ✔✔ (2)
10.7 Advantage turbocharger:
- Uses the exhaust gases and not power from the engine, to operate. ✔ (1)
10.8 Blower:
- Roots blower ✔✔ (2) [20]
TOTAL [200]