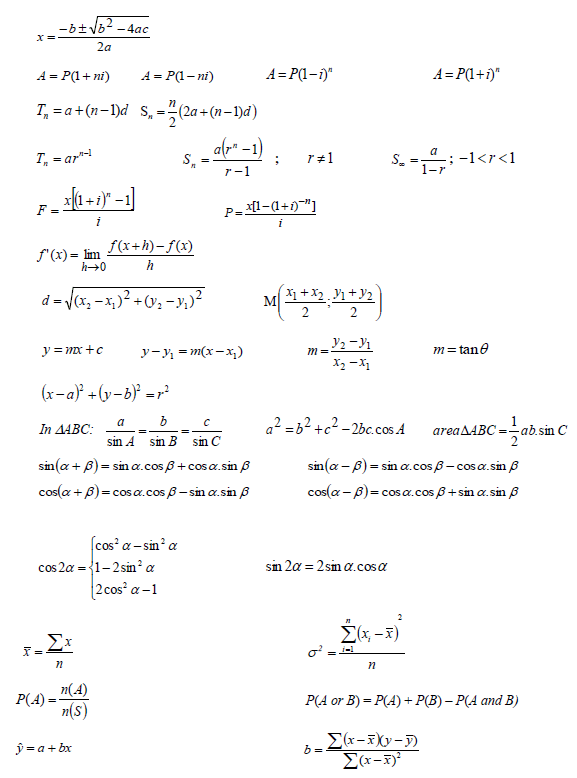MATHEMATICS PAPER 1 QUESTIONS GRADE 12 - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
NATIONAL SENIOR CERTIFICATE
GRADE 12
SEPTEMBER 2018
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of ELEVEN questions. Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answer.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- Answers only will not necessarily be awarded full marks.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- Number the answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
- An information sheet with formulae is included at the end of the question paper.
QUESTION 1
1.1 Solve for ?:
1.1.1 ½?2 − ? − 4 = 0 (3)
1.1.2 −3(?2 + 3?) + 7 = 0 (correct to two decimal places) (4)
1.1.3 2?2 − 3? < 0 (4)
1.2 Solve for ? and ? simultaneously in the following equations:
? − 2? = 3 and 4?2 − 3 = −6? + 5?? (6)
1.3 Prove that the roots of 2?2 − (? − 1)? + ? − 3 = 0 are real for all real values of ?. (5)
1.4 Given: 32m = 3p , where ? ≠ 3.
3 - p
1.4.1 Calculate the value of ? if ? = 1,5 (2)
1.4.2 Calculate the value of ? if ? = 0 (2)
[26]
QUESTION 2
2.1 7? + 1 ; 2? + 2 ; ? − 1 are the first three terms of a geometric sequence.
Determine the values of ?. (5)
2.2 A car that has been moving at a constant speed begins to slow down at a constant rate. It travels 25 m in the first second, 20 m in the second second,
16 m in the third second and so on. Show that the total distance covered, before it stops, does not exceed 125 metres. (4)
2.3 In an arithmetic sequence the first term is 2, the last term is 29 and the sum of all the terms is 155. Calculate the common difference. (5)
[14]
QUESTION 3
A quadratic number pattern, ??=??2+??+? , has the following information: ?1=?5=24 and it has a constant second difference of 4.
Determine the equation of the general term of the quadratic pattern. (8)
[8]
QUESTION 4
See given diagram below: ?(?)=?? ; where ?>0 and (2 ;36) is a point on ?.
4.1 Determine the value of ?. (2)
4.2 Determine the equation of ?−1 (?) in the form ?= …… (2)
4.3 For which values of ? is ?−1 (?)≤0 ? (2)
4.4 Write down the range of ℎ if ℎ(?)= ?(?−3)+2 (2)
[8]
QUESTION 5
Sketched below are the graphs of ?(?)=??2+??+? and ?(?)=−?+5. A and B are the ?-intercepts of ?. ?(3/2;49/4) is the turning point of ? . B and S are the points of intersection of ? and ?.
5.1 Calculate the coordinates of B. (2)
5.2 Determine the equation of ? in the form ?=??2+??+? (4)
5.3 If ?(?)=−?2+3?+10, calculate the coordinates of S. (4)
5.4 Use the graphs to solve for ? where:
5.4.1 ?(?)≥?(?) (2)
5.4.2 −?2+3?−2¼<0 (3)
[15]
QUESTION 6
Given: ?(?)=2/?−1
6.1 Draw a neat sketch of ? indicating all intercepts and asymptotes. (4)
6.2 Determine ?′(?) . (2)
6.3 Determine the equation of ℎ , the axis of symmetry of ? that has a negative gradient. (2)
6.4 A constant value ? is added to ℎ so that the straight line becomes a tangent to the graph of ? with ?>0. Determine the value of ?. (5)
[13]
QUESTION 7
7.1 Jack and Jill invest R2 000 each at different banks. Jack invests his R2 000 at 8% interest per annum compounded monthly and Jill invests her R2 000 at ? % interest per annum compounded semi-annually. Their investment is worth the same after 12 months. Calculate Jill’s investment rate. (3)
7.2 Anne bought a notebook laptop for R9 500. If the annual rate of depreciation was 7,7% per annum, how many years did it take for the notebook to depreciate to R4 500? (5)
7.3 Raeez buys a car for R170 500. He pays 25% deposit and takes out a loan for the balance. The bank charges interest at 13,2% per annum compounded monthly.
7.3.1 Determine the value of his loan. (2)
7.3.2 Calculate the monthly repayment if the loan is to be repaid over 5 years and the first instalment is made one month after the loan has been granted. (5)
[15]
QUESTION 8
8.1 Given: ?(?) = ? − 2?2
Determine ?′(?) from first principles. (6)
8.2 Determine dy/dx if:
8.2.1 ? = 1/9?−3 + 9? (2)
8.2.2 ? =− 1 + ?3 (4)
2?√?
[12]
QUESTION 9
The sketch below shows the graph of ℎ(?) = ?3 − 9?2 + 23? − 15. C and E are the turning points of ℎ. B , D and F are the x-intercepts of ℎ and A is the ?-intercept.
9.1 Determine the x-coordinate of the turning point C, correct to two decimal places. (4)
9.2 If the ?-coordinate of B is 1 , determine the coordinates of F. (4)
9.3 The graph of ℎ is concave down for ? < ?. Calculate the value of ?. (3)
9.4 Determine the equation of the tangent at D in the form ? = . . . … (3)
[14]
QUESTION 10
In a home industry, the total cost (in rand) of producing ? number of cakes per day is ?(¼?2+35?+25). The price at which they are sold is ?(50−½?) each.
10.1 Show that the profit made is given by the formula: ?=−3/4?2+15?−25. (2)
10.2 Calculate the daily output of cakes to obtain maximum profit. (3)
10.3 Show that the cost of baking is a minimum at ?=10. (5)
[10]
QUESTION 11
11.1 In a survey done at a local traffic department, the following information was obtained.
| Failed | Passed | Total | |
| Male | A | B | 1200 |
| Female | C | D | 400 |
| Total | 200 | 1400 | 1600 |
11.1.1 Calculate the probability that a person selected at random will be male. (1)
11.1.2 Calculate the probability that a person selected at random failed the test. (1)
11.1.3 If being male and failing the test are independent events, show that the value of A = 150. (3)
11.1.4 Use the value of A to determine the values of B, C and D. (3)
11.1.5 Calculate the probability of choosing a female that has failed. (2)
11.2 9 cars of different makes of which 4 are black are to be parked in a straight line.
11.2.1 In how many different ways can all the cars be parked? (2)
11.2.2 If the 4 black cars must be parked next to each other, determine in how many different ways the cars can be parked. (3)
[15]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS