GRADE 12 MATHEMATICS SCHOOL BASED ASSESSMENT EXEMPLARS - CAPS LEARNER'S GUIDE
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupGRADE 12 MATHEMATICS
SCHOOL BASED ASSESSMENT EXEMPLARS - CAPS
LEARNER'S GUIDE
| Table of Contents | ||
| Contents | Page | |
| 1 | ASSIGNMENT Sequences and series | 4 |
| 2 | INVESTIGATION 1 | 6 |
| 3 | INVESTIGATION 2 | 12 |
| 4 | PROJECT A practical application of differential calculus | 14 |
INTRODUCTION
One of the aims of our curriculum is to ensure that learners acquire and apply knowledge and skills in ways that are meaningful to their own lives. In this regard, and where applicable, the assessment tasks in this document seek to test practical knowledge in context.
The table below shows the school-based assessment requirements for the year. Please note that although the project/ investigation is indicated in the first term, it may be scheduled in the second term.
SCHOOL-BASED ASSESSMENT | ||
TASK | WEIGHT (%) | |
Term 1 | Test | 10 |
Term 2 | Test | 10 |
Term 3 | Test | 10 |
School-based assessment as a % of the promotion mark | 25% | |
1. ASSIGNMENT: SEQUENCES AND SERIES TOTAL: 60 INSTRUCTIONS
- Answer all the questions.
- Clearly show all calculations you have used in determining your answers.
- Round answers off to TWO decimal places, unless stated otherwise.
- Number your answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
QUESTION 1
Lucy is arranging 1-cent and 5-cent coins in rows. The pattern of the coins in each row is shown below.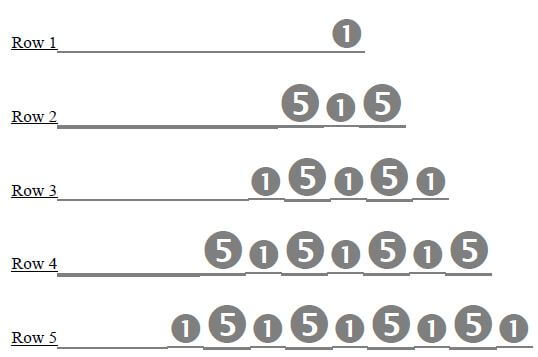
1.1 Calculate the total number of coins in the 40th row. (3)
1.2 Calculate the total value of the coins in the 40th row. (4)
1.3 Which row has coins with a total value of 337 cents? (6)
1.4 Show that the total value of the coins in the first 40 rows is 4 800 cents. (6)
[19]
QUESTION 2
The sum of the first n terms of a sequence is given by: Sn = n(23 – 3n)
2.1 Write down the first THREE terms of the sequence. (5)
2.2 Calculate the 15th term of the sequence. (3)
[8]
QUESTION 3
The sum of the second and third terms of a geometric sequence is 280, and the sum of the fifth and the sixth terms is 4 375. Determine:
3.1 The common ratio AND the first term (6)
3.2 The sum of the first 10 terms (2)
[8]
QUESTION 4
Determine the value of k if: ![]() [6]
[6]
QUESTION 5
Given the series: 2(5)5 + 2(5)4 + 2(5)3 + ...
Show that this series converges.
[2]
QUESTION 6
If 2; x; 18; ... are the first three terms of a geometric sequence, determine the value(s) of x.
[4]
QUESTION 7
Given Tn = 3n+1 . Which term is the first to exceed 20 000?
[4]
QUESTION 8
The sequence 3; 9; 17; 27; ... is a quadratic sequence.
8.1 Write down the next term of the sequence. (1)
8.2 Determine an expression for the nth term of the sequence. (4)
8.3 What is the value of the first term of the sequence that is greater than 269? (4)
[9]
TOTAL: 60
2. INVESTIGATION 1: FUNCTIONS AND INVERSES TOTAL: 50
INSTRUCTIONS
- Answer all the questions.
- Clearly show all calculations you have used in determining your answers.
- Round answers off to TWO decimal places, unless stated otherwise.
- Number your answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
PART 1: WHICH RELATIONS CONSTITUTE FUNCTIONS?
One-to-one relation: A relation is one-to-one if for every input value there is only one output value.
Many-to-one relation: A relation is many-to-one if for more than one input value there is one output value.
One-to-many relation: A relation is one-to-many if for one input value there is more than one output value.
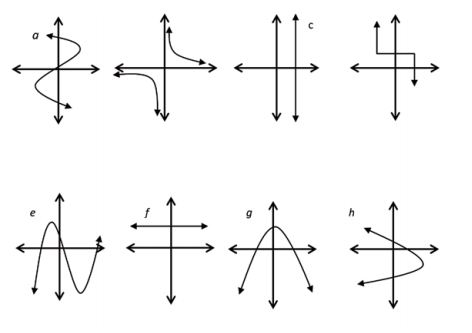
1.1 Determine the type of relation in each case and give a reason.
1.1. 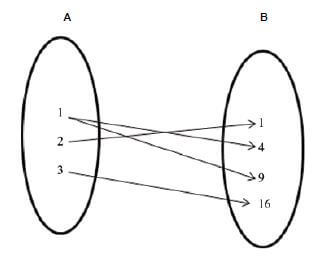 (1)
(1)
1.1.2 {(1 ; 3), (2 ; 5), (6 ; 13), (7 ; 15)} (1)
1.1.3 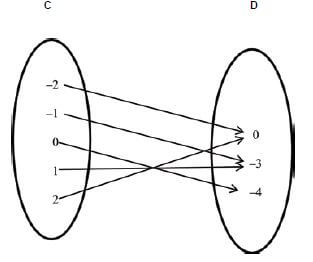 (1)
(1)
A function is a set of ordered number pairs where no two ordered pairs have the same x-coordinate, or put differently: a function is a set of ordered pairs where, for every value of x there is one and only one value for y. However, for the same value of y there may be different values for x.
1.2 Which of the relations (in QUESTIONS 1.1.1 to 1.1.3) are functions? Why?
- _______________________________________________________________ (2)
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
The vertical-line test is used to determine whether or not a given graph is a function.
To determine whether a graph is a function, do the vertical-line test. If any vertical line intersects the graph of f only once, then f is a function; and if any vertical line intersects the graph of f more than once, then f is not a function.
1.3 Determine whether or not the following graphs are functions. Give a reason for your answer.
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
- _______________________________________________________________ (1)
- ______________________________________________________________ (1)
PART 2: THE INVERSE OF AN EXPONENTIAL FUNCTION
2.1 Consider the equation g(x) = 2x. Now complete the following table:
x | – 3 | – 2 | – 1 | 0 | 1 | 2 |
y |
(1)
2.2 Sketch the graph of g. 
2.3 Sketch the graph of f(x) = x as a dotted line on the same set of axes as g. (1)
2.4 Complete the table below for h, if h is g when the x and y values are interchanged.
x | ||||||
y |
Draw h on the same set of axes as g. (4)
2.5 Hence, write down the x-intercept of each graph.
y = 2x x = 2y
2.5.1___________________________________________________________
2.5.2___________________________________________________________ (2)
2.6 Write down the domain and range of:
2.6.1 y = 2x
Domain: ___________________
Range: ____________________ (2)
2.6.2 x = 2y
Domain:____________________
Range:______________________ (2)
2.6.3 What is the relationship between the domain and the range of the two graphs? (1)
2.6.4 Are both graphs functions? Give reasons. (2)
2.6.5 Write the equation of x = 2y in the form y = (1)
2.6.6 Do you notice any line of symmetry in your sketch? What is the equation of this line? (1)
2.6.7 In mathematics we call h the inverse of g. Make a conjecture about the graph and its inverse. (3)
PART 3: WHEN IS THE INVERSE OF A QUADRATIC FUNCTION ALSO A FUNCTION?
3.1 Given: f (x) = 2x2, for
3.1.1 Write down the equation of the inverse of f. (1)
3.1.2 Write down the turning points of both f and its inverse. (2)
3.1.3 Sketch the graphs of f and its inverse on the same set of axes. (2)
3.1.4 Decide whether or not the inverse of f is a function, and give a reason for your answer. (2)
3.1.5 Explain how you would restrict the domain of f such that its inverse is a function. (2)
3.1.6 Hence, write down the corresponding range of the inverse of f if:
- x ≤ 0 _______________________________________________ (1)
- x ≥ 0 _______________________________________________ (1)
3.1.7 On separate sets of axes, sketch the graphs of the inverse of f with restricted domains as in QUESTION 3.1.6. Indicate the domain and range of each. (2)
3.1.8 Are the two graphs in QUESTION 3.1.7 functions? Give a reason or reasons for your answer. (2)
TOTAL: 50
3. INVESTIGATION 2: APPLICATION OF DIFFERENTIAL CALCULUS TOTAL: 50
INSTRUCTIONS
- Answer all the questions.
- Clearly show all calculations you have used in determining your answers.
- Round answers off to TWO decimal places, unless stated otherwise.
- Number your answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly.
OBJECTIVE: Investigating the point of inflection of a cubic graph and its relationship with the graphs of the first and the second derivatives.
CASE 1
Given: f (x) = x3 – 7x2 + 36
1.1 Draw the graph of f neatly on graph paper. Clearly indicate all intercepts and coordinates of turning points. (8)
1.2 Determine the first derivative of f, and name it g. (1)
1.3 Draw the graph of g on the same set of axes as f. Clearly show all intercepts and the turning point. (3)
1.4 Determine the second derivative of f and name it h. Then sketch the graph of h on the same set of axes as f and g. Clearly show all intercepts of the graph with the axes. (3)
1.5 What do you notice regarding the x-intercepts of the quadratic function and the x-coordinates of the turning points of the cubic function? (1)
1.6 The point of inflection can be determined by solving f “(x) = 0. It can also be determined by calculating the midpoint of the turning points of the cubic graph.
Hence, determine the point of inflection of f. (3)
1.7 What do you notice regarding the axis of symmetry of g, the x-intercept of h and the x-coordinate of the point of inflection of f ? (1)
[20]
CASE 2
Given: f (x) = – x3 – 2x2 + 4x + 8
2.1 Draw the graph of f neatly on graph paper. Clearly indicate all intercepts and coordinates of turning points. (7)
2.2 Determine the first derivative of f, and name it g. (1)
2.3 Draw the graph of g on the same set of axes as f, and clearly show all intercepts and the turning point. (4)
2.4 Determine the second derivative of f and name it h, then sketch the graph of h on the same set of axes as f and g. Clearly show all intercepts of the graph with the axes. (3)
2.5 What do you notice regarding the x-intercepts of the quadratic function and the x-coordinates of the turning points of the cubic function? (1)
2.6 The point of inflection can be determined by solving f “ (x) = 0. It can also be determined by calculating the mid point of the turning points of the cubic graph.
Hence, determine the point of inflection of f. (3)
2.7 What do you notice regarding the axis of symmetry of g, the x-intercept of h and the x-coordinate of the point of inflection of f ? (1)
[20]
3. CONCLUSION
Based on the two cases, what conclusion can you draw about the point of inflection of a cubic function in relation to the graphs of the first and second derivatives? [2]
4. APPLICATION
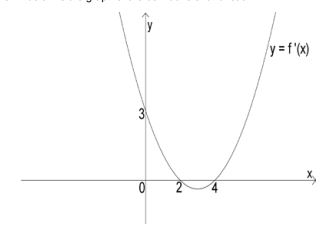
The parabola shown below is the graph of the derivative of a function f.
4.1 For what value(s) of x is f :
4.1.1 Increasing (2)
4.1.2 Decreasing (2)
4.2 Give the abscissae of the turning point(s) of y = f (x). (2)
4.3 Classify the stationary point(s). (2)
[8]
TOTAL: 50
4. PROJECT: A PRACTICAL APPLICATION OF DIFFERENTIAL CALCULUS TOTAL: 50
INSTRUCTIONS
- Answer all the questions.
- Clearly show all calculations you have used in determining your answers.
- Round answers off to TWO decimal places, unless stated otherwise.
- Number your answers correctly according to the numbering system used in this question paper.
- Write neatly and legibly,
- Sketch the containers according to the given specifications.
- Mathematical methods and formulae need to be used to plan and sketch the containers.
- All calculations and planning of the side lengths and surface areas must be neatly and clearly presented in writ ing and sketches.
CONTAINERS
- : A container with a rectangular base
- : A container with a circular base
- : A container with a triangular base
SPECIFICATIONS
- Each container must hold exactly one litre of liquid.
- Each container must have a minimum surface area.
- The surface area of each container must include the lid.
- The length of the rectangular base must be twice the breadth.
- The triangular container must have an equilateral base.
FURTHER COMPARISON
Apart from your conclusion based on the three options, what other shape of soft drink container would you use in the manufacturing of soft drink cans? Give a reason for your answer.
HINT: The shape in question would be the most economical to manufacture but may not be the most practical choice.
RUBRIC
CRITERIA | MAXIMUM MARK | MARKS AWARDED | ||
A | B | C | ||
Correct mathematical formulae | 3 x 3 | |||
Correct calculations: | ||||
Measurements of bases | 4 x 3 | |||
Height of the containers | 2 x 3 | |||
Logical reasoning and presentation | 3 x 3 | |||
Submitting on time | 2 | |||
Conclusion of the least material needed | 1 x 3 | |||
Final, further comparison | 1 x 3 | |||
Sketches | 2 x 3 | |||
TOTAL | 50 | |||