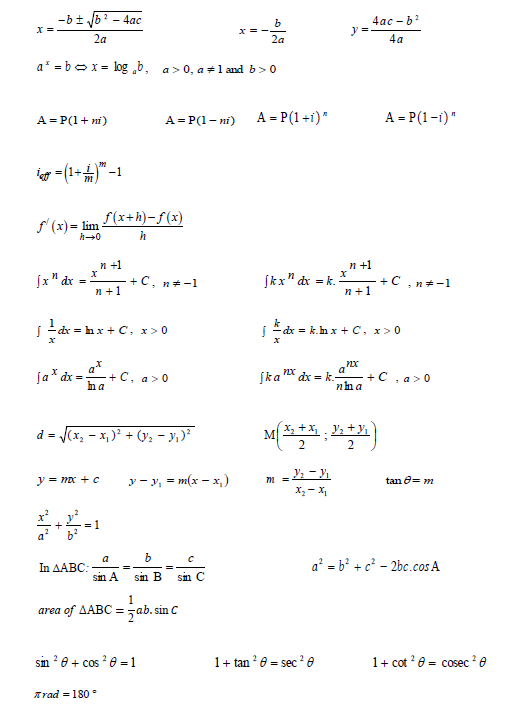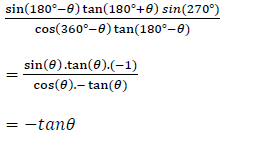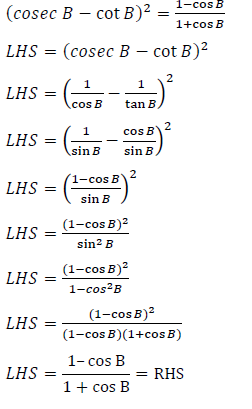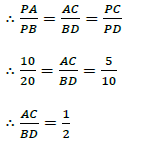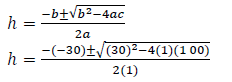TECHNICAL MATHEMATICS P2 with Memorandum - 2024 Grade 12 June Common Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMARKS: 150
TIME: 3 hours
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
1. This question paper consists of ELEVEN questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
4. Answers only will NOT necessarily be awarded full marks.
5. You may use an approved scientific calculator (non-programmable and non graphical) unless stated otherwise.
6. If necessary, round off your answers to TWO decimal places, unless stated otherwise.
7. Diagrams are NOT necessarily drawn to scale.
8. An information sheet with formulae is included at the end of the question paper.
9. Write neatly and legibly.
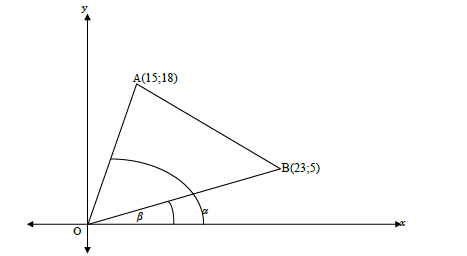
QUESTION 1
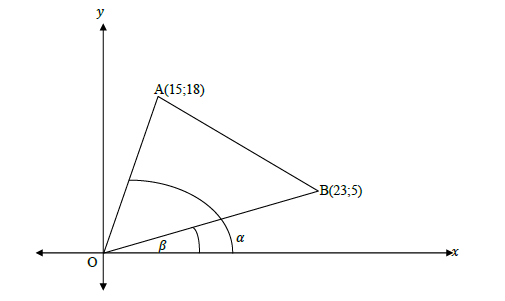
In the diagram below, AOB is a triangle with vertices A(15 ; 18); O(0 ; 0) and B(23 ; 5). β is the angle of inclination of line OB and α is the angle of inclination of line OA.
1.1 Determine the gradients of OA and OB. (4)
1.2 Determine the angle of inclination of line OB. (3)
1.3 Find the size of AOB, correct to the nearest whole number. (4)
1.4 AOBM is a parallelogram. Find the coordinates of M. (5) [16]
QUESTION 2
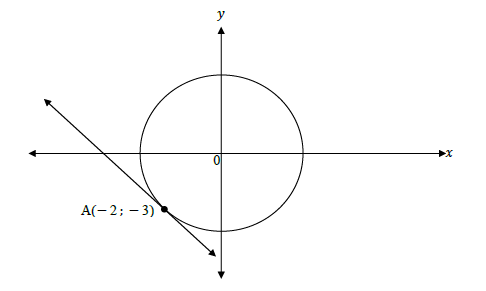
2.1 The diagram below shows the circle with equation x2 + y2 = 13. The contact point of a tangent to the circle is at A(− 2 ; − 3).
2.1.1 Write down the radius of the circle in simplified surd form. (1)
2.1.2 Determine the equation of the tangent to the circle at point A in the form y = . .. (4)
2.1.3 Write down the coordinates of another point where the line AO intersects with the circle. (2)
2.2 Sketch the graph of 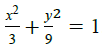
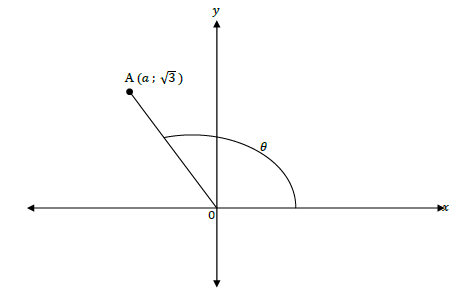
QUESTION 3
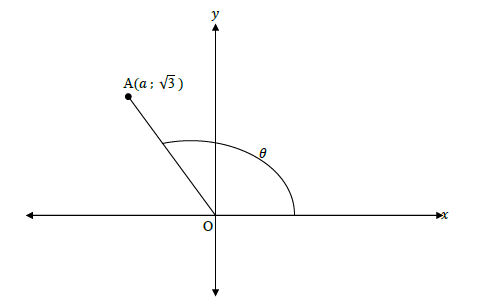
3.1 In the diagram below A(a ; √3 ) and OA = 3.
Determine the value of the following, without using a calculator:
3.1.1 a (3)
3.1.2 sec θ (1)
3.1.3 cosec (θ + 360°) (3)
3.2 Determine the values of x, if tan(x − 30°) = −0,982 and 0° ≤ x − 30° ≤ 360°. (4) [11]
QUESTION 4
4.1 Simplify: [sin(180°− θ )tan(180° + θ)sin(270°)] ÷ cos(360°− θ)tan(180°− θ) (6)
4.2 Prove that: (cosec B − cot B )2 = (1 + cos B) ÷ (1 − cos B) (6) [12]
QUESTION 5
Given the functions defined by f(x) = cos(x − 30) and g(x) = 2 sin x for x ∈ (0° ;360°).
5.1 Write down the period of f. (1)
5.2 Write down the amplitude of g. (1)
5.3 On the same axes, given in your SPECIAL ANSWER BOOK, draw the graphs of f and g. Clearly show the turning points, endpoints and the intercepts with the axes. (8)
5.4 Use your graphs to determine for which values of x is:
5.4.1 g(x) ≥ 0 (2)
5.4.2 f(x). g(x) <0 in the second quadrant (2) [14]
QUESTION 6
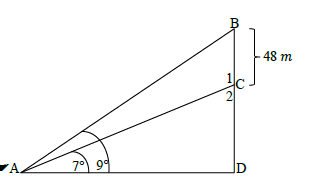
6.1 Write down the sine rule for ΔABD. (1)
6.2 A ship at sea, observes that the angles of elevation to the top and bottom of a lighthouse on a cliff are 7° and 9° respectively. It is known that the height of the lighthouse is 48 m.
6.2.1 The size of BAC, stating a reason (2)
6.2.2 The size of ABD, stating a reason (2)
6.2.3 The length of AC (4)
6.2.4 The distance between the ship and the bottom of the cliff (2)
6.2.5 The height of the cliff (3) [14]
QUESTION 7
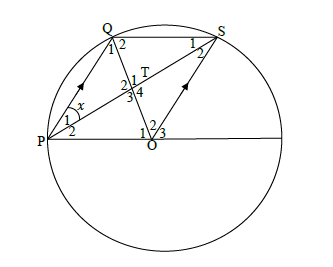
In the diagram below, O is the centre of the circle. OS ∥ PQ and PS meet OQ at T. Q S
7.1 If P1 = X, express T1 in terms of x. Give reasons. (6)
7.2 If x = 30°, calculate the sizes of the angles in ΔQST. Give reasons where necessary. (5)
7.3 Show that ΔPQS ≡ ΔSOP. (3) [14]
QUESTION 8
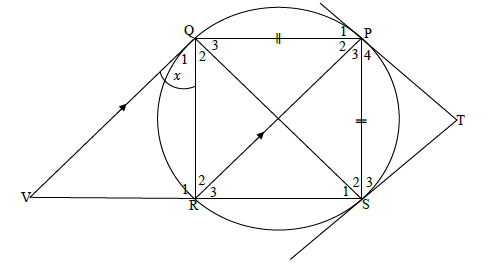
PQRS is a cyclic quadrilateral with PS = PQ. SR is produced to meet V such that PR ∥ QV. TP and TS are tangents to the circle. Q1 = x .
8.1 Name, with reasons, four other angles equal to x. (8)
8.2 Give a reason for P4 = S3. (1)
8.3 Prove, with reasons, that T = QPS. (5) [14]
QUESTION 9
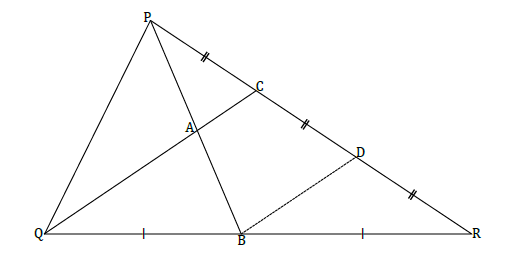
In the diagram below, B is the midpoint of side QR. C and D are points on PR such that PC = CD = DR. PR = 15 cm.
9.1 Show that BD ∥ QC. (3)
9.2 Prove that PA = AB. (3)
9.3 Determine the length of QR, if PD : DR = 2 : 1. (6) [12]
QUESTION 10
A fan in a jet engine has a diameter of 340 cm and a circumferential velocity of 568 metres per second.
10.1 Convert 568 m/s to km/h. (2)
10.2 Determine the rotational frequency of the wheel in hours. (5)
10.3 Determine the angular velocity of the wheel in seconds. (3)
10.4 Determine the distance, in km, a point on the fan will cover in 15 seconds. (3)
10.5 Determine how long it will take the fan to make half a revolution. (2) [15]
QUESTION 11
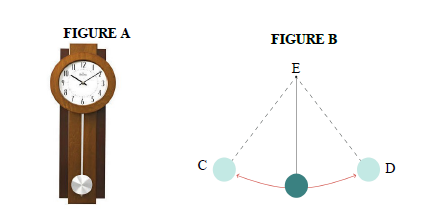
11.1 A pendulum in a clock, FIGURE A, follows the path as depicted in the diagram below, FIGURE B. There is a radius of 30 cm and the angle formed is 60°.
11.1.1 Determine the length of arc CD, that the pendulum follows. (3)
11.1.2 Determine the area of sector ECD. (3)
11.1.3 Calculate the length of the pendulum. (3)
11.2 An analogue clock has a diameter of 30 cm, and a chord length of 20 cm.
Determine the length of the hour hand. (5)
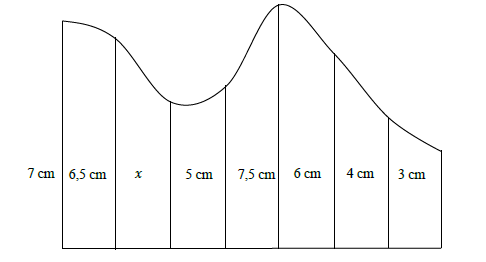
11.3 The ordinates in the irregular figure are: 7 cm, 6,5 cm, x , 5 cm; 7,5 cm, 6 cm, 4 cm and 3 cm respectively as indicated in the diagram below. The width of the irregular figure is 11,55 cm and the area is 63,525 cm2.
Determine the length of the unknown ordinate x. (4) [18]
TOTAL: 150
INFORMATION SHEET: TECHNICAL MATHEMATICS
Angular velocity = ω = 2 π n where n = rotation frequency
Angular velocity = ω = 360° n where n = rotation frequency
Circumferential velocity= v = π Dn where D = diameter and n = rotation frequency
Circumferential velocity= ν = ωr where ω= Angular velocity and r = radius
Arc length s = rθ where r = radius and θ = central angle in radians
Area of a sector 2r/s = where r = radius, s = arc length
MARKING GUIDELINE
NOTE:
- Continuous accuracy (CA) applies only where indicated in this marking guideline.
- Assuming values/answers in order to solve a problem is unacceptable.
MARKING CODES / NASIENKODES | |
M | Method/Metode |
A | Accuracy/Akkuraatheid |
AO | Answer only/Slegs antwoord |
CA | Consistent accuracy/Deurlopende akkuraatheid |
F | Formula/Formule |
I | Identity/Identiteit |
R | Rounding/Afronding |
S | Simplification/Vereenvoudiging |
ST | Statement/Bewering |
RE | Reason/Rede |
ST RE | Statement and correct reason/Bewering en korrekte rede |
SF | Substitution correctly in correct formula/Korrekte vervanging in die korrekte formule |
NPU | No penalty for omitting units/Geen penalisering vir eenhede uitgelaat |
| ||
1.1 | mOA = (18 − 0) ÷ (15 − 0) mOA =6/5 mOB = (5 − 0) ÷ (23 − 0) mOB =5/23 AO: Full marks / Volpunte | ✓ M ✓ S A ✓ M ✓ S A (4) |
1.2 | tan β = mOB tan β =5/23 ∴ β = 12,26° | ✓ M ✓ Subst./Vervang A ✓ S CA n(3) |
1.3 | tan α = mOB tan α =65 ∴ α = 50,19° ∴ AOB = 50,19° − 12,26° = 37,93° ≈ 38° | ✓ M ✓ Subst. A ✓ S CA ✓ Answer/Antwoord CA (4) |
1.4 | 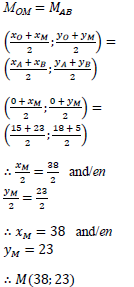 | x-coordinate of /koördinate van M =23+15 =38 y-coordinate of /koördinate M = 23 + 15 =38 M(38;23) (If learner used this method award full marks/Indien leerling hierdie metode gebruik ken volpunte toe.) | ✓ M ✓ Subst. A ✓ M CA ✓ S CA ✓ Answer/Antwoord CA (5) |
[16] | |||
2.1 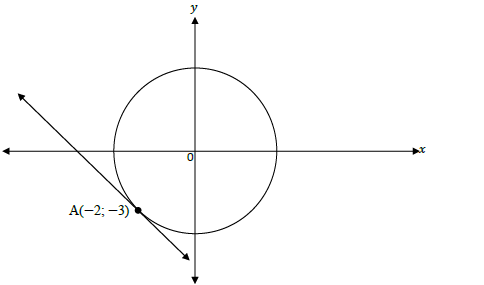 | ||
2.1.1 | r = √13 | ✓ A (1) |
2.1.2 | 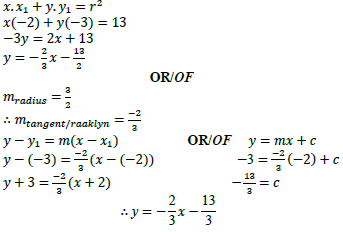 | ✓ F ✓ SF A ✓ S ✓ equation / vergelyking CA OR/OF ✓ grad. radius A ✓ grad. tan / raaklyn CA ✓ SF A ✓ equation / verglyking CA (4) |
2.1.3 | (3 ; 2) | ✓ x-value/waarde A ✓ y-value/ waarde A (2) |
2.2 | ✓ elliptical shape / elliptiese vorm A ✓ x-intercepts / afsnitte A ✓ y-intercepts / afsnitte A (3) | |
[10] |
3.1 | ||
3.1.1 | a2 + (√3)2= (3)2 a2 = 9 − 3 a2 = 6 a = ±√6 ∴ a = −√6 | ✓ M ✓ S ✓ value of / waarde van a (3) |
3.1.2 | −√6 / 3 | ✓ Answer/Antwoord (1) |
3.1.3 | cosec (θ + 360°) = cosec θ ∴ cosec θ =3 / √3 | ✓ Reduction/ Reduksie A ✓✓ cosec ratio / verh. CA (3) |
3.2 | tan (x − 30°) = −0,982 Ref. /Verw. < = tan-1(0,982) Ref. /Verw. < = 44,48° ∴ I: x − 30° = 180° − 44,48° ∴ x = 165,52° AND/EN ∴ IV: x − 30° = 360° − 44,48° ∴ x = 345,52° | ✓ Ref. / Verw. ∠ CA ✓ Quadrants / kwadrante A ✓✓ values of x / waardes van x CA (4) |
[11] | ||
4.1 | ✓ sin(θ) A | |
4.2 | 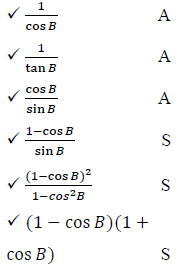 | |
[12] |
QUESTION/VRAAG 5
f(x) = cos(x − 30) and /en g(x) = 2 sin x for/ vir x ∈ (0° ; 360°) | ||
5.1 | periodf = 360° | ✓ A (1) |
5.2 | Amplitudeg = 2 | ✓ A (1) |
5.3 | 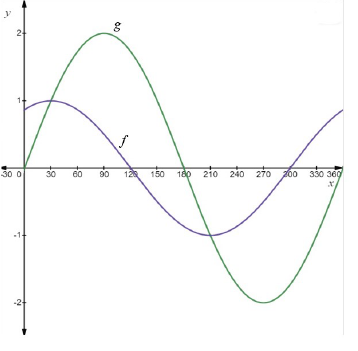 | f: ✓ y-intercept at / y-afsnit by 0,87 ✓ x-intercepts at 120° and 300° x-afsnitte by 120° en 300° ✓✓ turning point at / draaipunt by (30°; 1) and/en (210° ; -1) g: ✓ y-intercept at / y-afsnit by 0 ✓ x-intercept at 180° and 360° / x-afsnit by 180° en 360° ✓✓ turning point at / draaipunt by (90°; 1) and/en (270° ; -1) (8) |
5.4.1 | 0° ≤ x ≤ 180° | ✓0° ≤ x CA ✓x ≤ 180° CA (2) |
5.4.2 | 120° < x < 180° and /en 300° < x < 360° | ✓120° < x < 180° CA ✓300° < x < 360° CA (2) |
[14] | ||
QUESTION/VRAAG 6
6.1 | a/sin A = b/sinB = d/sinD | ✓ A (1) |
6.2 | 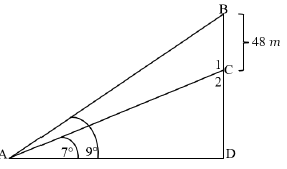 | |
6.2.1 | BAC = 9° − 7° = 2° (given/gegee) | ✓ ST A ✓ RE (2) |
6.2.2 | ABD = 180° − 9° − 90° = 81° (int. <’s of Δ / binne <’e van Δ) | ✓ ST A ✓ RE (2) |
6.2.3 | 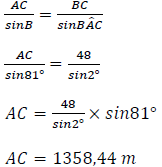 | ✓ F |
6.2.4 | 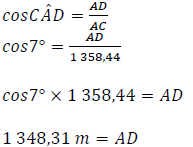 | ✓ ratio / verh. A ✓ value / waarde CA (2) |
6.2.5 | AC2 = AD2 + CD2 (1 358,44)2 = (1 348,31)2 + CD2 27419,3775 = CD2 165,59 m = CD | ✓ F ✓ SF CA ✓ height / hoogte CA (3) |
[14] | ||
QUESTION/VRAAG 7
7.1 | S2 = X (alt. <’s = / verw. <’e =; PQ∥SO) O2 = 2x (< at centre = 2×< at circumf. /midpts< = 2× omtreks<) T1 = 3x (ext. < of Δ / buite < van Δ) | ✓ ST |
7.2 | T1 = 3x T1 = 3(30°) = 90° O2 = 2x O2 = 2(30°) = 60° ∴ Q2 = 60° (OQ = OS; Radii) ∴ S1 = 30° | ✓ T1 CA ✓ O2 CA ✓ Q2 ✓RE CA ✓ S1 CA(5) |
7.3 | In Δ PQS and/en Δ SOP: 1. S2 = S1 (proven / bewys) 2. QS = PO (given / gegee) 3. P1 = P2 (given / gegee) ∴ Δ PQS ≡ Δ SOP (<<S) | ✓ ST A ✓ ST A ✓ ST A (3) |
[14] |
QUESTION/VRAAG 8
8.1 | S1 = x (tan-chord thm / stelling) P2 = x (<’s in same segment / <’e in dieselfde segment) R2 = x (alt. <’s = / verw. <’e =; VQ∥RP) S2 = x (<’s in same segment / <’e in dieselfde segment) | ✓ ST ✓ RE A ✓ ST ✓ RE A ✓ ST ✓ RE A ✓ ST ✓ RE A (8) |
8.2 | Tangents from same point / Raaklyne vanuit dieselfde punt | ✓ RE A (1) |
8.3 | P4 = R3 = x (tan-chord thm / stelling) ∴ T = 180° − 2x (int. <’s of Δ / binne <’e van Δ) P2 + P3 = 180° − 2x (int. <’s of Δ / binne <’e van Δ) ∴ T= QPS | ✓ ST ✓ RE A ✓ ST ✓ RE A ✓ ST A (5) |
[14] | ||
QUESTION/VRAAG 9
| ||
9.1 | In ΔCRQ: RD = DC (given / gegee) RB = BQ (given / gegee) ∴ BD ∥ CQ and/en BD = ½ CQ (midpt thm / stelling) | ✓ ST A ✓ ST A ✓ RE A (3) |
9.2 | In ΔPBD: PC = CD (given / gegee) BD ∥ CQ (given / gegee) ∴ PA = AB and/en AC = ½ BD (midpt thm / stelling) | ✓ ST A ✓ ST A ✓ RE A (3) |
9.3 | Δ PAC and/en Δ PBD: 1. P = P (common < / gemene <) 2. PAC = PBD (Corresp. <’s = / ooreenk. <’e =; AC∥BD) 3. PCA = PDB (3rd < of Δ / 3de < van Δ) ∴ Δ PAC lll Δ PBD (<<<) ∴ BD : AC = 2 : 1 | ✓ ST A ✓ ST A ✓ ST A ✓ ST A ✓ Subst./Vervang A ✓ Answer/Antwoord A (6) |
[12] | ||
QUESTION/VRAAG 10
10.1 | ✓ conversion factors / herleidingsfaktore ✓ answer / antwoord (2) | |
10.2 | 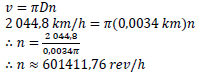 | ✓F ✓ conversion / herleiding ✓ SF A ✓ S ✓ answer / antwoord (5) |
10.3 | ω π = 2 n = × 2 38,20 π ≈ 240,02 rad/s | ✓F ✓ SF CA ✓ answer / antwoord (3) |
10.4 | s = vt OR / OF D = ST s = 0,568 × 15 s = 8,52 km | ✓F ✓ SF CA ✓ answer / antwoord (3) |
10.5 | n = number of revolutions / time 53,18 =1/2 ⁄ t ∴ t ≈ 0,009 sec/sek | ✓ SF CA ✓ answer / antwoord (2) |
[15] |
QUESTION/VRAAG 11
 | ||
11.1.1 | s = rθ s = (30) (60° ×π/180°) ∴ CD = 10π ≈ 31,42 cm | ✓F ✓ SF A ✓ RT length / lengte (3) |
11.1.2 | 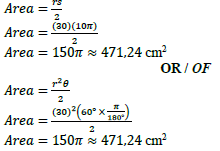 | ✓F ✓ SF A ✓ Area OR / OF ✓F ✓ SF A ✓ Area (3) |
11.1.3 | D = 2r D = 2(30) ∴ D = 60 cm | ✓M ✓Subst./Vervang ✓ Answer/Antwoord (3) |
11.2 |  | |
4ℎ2 − 4dℎ + x2 = 0 4ℎ2 − 4(30)ℎ + (20)2 = 0 4ℎ2 − 120ℎ + 400 = 0 ℎ2 − 30ℎ + 100 = 0 ∴ ℎ = 3,82 cm ∴ h hour hand length/lengte van uur aanwyser = radius−height of minor segment/hoogte van kleiner segment ∴ hour hand length/lengte van uur aanwyser = (30/2) − 3,82 ∴ hour hand length/lengte van uuraanwyser = 11,2 cm | ✓F ✓SF A ✓S ✓ value of / van ℎ ✓ length/lengte (5) | |
11.3 | 3 cm | |
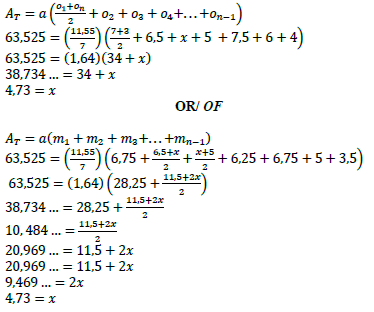 | ✓F ✓SF A ✓S ✓ value of/waarde van a OR/ OF ✓F ✓SF A ✓S ✓ value of/ waarde van a (4) | |
[18] | ||
TOTAL/TOTAAL: | 150 |