MATHEMATICS INVESTIGATION: 2023
GRADE 12
NATIONAL SENIOR CERTIFICATE

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This task paper consists of 2 questions.
2. Answer ALL the questions.
3. Number the answers correctly according to the numbering system used in this question paper
4. Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining your answers.
5. Answers only will not necessarily be awarded full marks.
6. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
7. If necessary, answers should be rounded off to TWO decimal places, unless stated otherwise.
8. Diagrams are NOT necessarily drawn to scale.
9. Write neatly and legibly.

INVESTIGATING COMPOUND ANGLES
QUESTION 1
1.1. In the following diagrams, 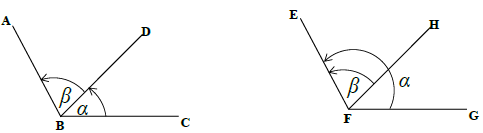𝐴𝐵𝐷 = 𝛽, 𝐷𝐵𝐶 = 𝛼, 𝐸𝐹𝐻 = 𝛽, 𝐸𝐹 𝐺 = 𝛼

Write each of the following in terms of α and β
1.1.1 𝐴𝐵 # 𝐶 _________________________ (1)
1.1.2 𝐻𝐹 # 𝐺 _________________________ (1)
1.2 Use your calculator to complete the table below. There is no need to show your working out.

(10)
1.2.2 What do you notice concerning the values of 𝑐𝑜𝑠(𝛼 − 𝛽) 𝑎𝑛𝑑 𝑐𝑜𝑠𝛼 − 𝑐𝑜𝑠𝛽 ?
(Hint – are the values the same or different?) (1)
1.2.3 What do you notice concerning the values of cos(𝛼 − β) and 𝑐𝑜𝑠𝛼𝑐𝑜𝑠𝛽 + 𝑠𝑖𝑛𝛼𝑠𝑖𝑛𝛽 (1)
1.2.4 What do you notice concerning the values of cos(𝛼 − β) and 𝑐𝑜𝑠𝛼𝑐𝑜𝑠𝛽 − 𝑠𝑖𝑛𝛼𝑠𝑖𝑛𝛽? (1)
1.2.5 Hence deduce a formula to expand cos(𝛼 − β) (2)
[17]

SECTION B
QUESTION 2
2.1 Now let us investigate whether the identity of cos(𝛼 − β) = 𝑐𝑜𝑠𝛼𝑐𝑜𝑠𝛽 + 𝑠𝑖𝑛𝛼𝑠𝑖𝑛𝛽 is true for all values of α and β.
Let P (cos𝛼; 𝑠𝑖𝑛𝛼) and Q (cos𝛽; 𝑠𝑖𝑛𝛽) be any two points on the circle O with radius 1. If 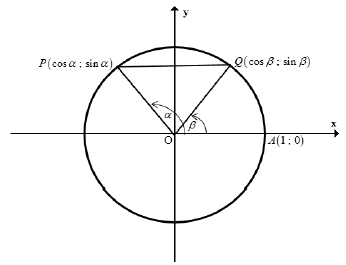𝑃𝑂𝐴 = 𝛼 and 𝑄𝑂𝐴 = 𝛽 then 𝑃𝑂𝑄 = 𝛼 − 𝛽

2.1.1 Make use of the cosine rule to determine the length of PQ. (4)
2.1.2 Make use of the distance formula to determine the length of PQ  (5)
2.1.3 Hence, compare number 2.1.1 and 2.1.2 and write a conclusion about cos(a – b). (3)
2.1.4 Use 2.1.3 [cos(𝛼 − 𝛽) = 𝑐𝑜𝑠𝛼. 𝑐𝑜𝑠𝛽 + 𝑠𝑖𝑛𝛼. 𝑠𝑖𝑛𝛽 ] to derive a formula for cos(𝛼 + 𝛽)
(Hint: use suitable reduction formula) (4)
2.1.5 Use cos(a – b) to derive a formula for sin(a – b).
(Hint: use co-function) (3)
2.1.6 Use cos(a – b) to derive a formula for sin(a + b).
(Hint: use co-function) (3)
[22]

QUESTION 3
Applications
3.1 Express the following as single trigonometry ratio:
3.1.1 𝑐𝑜𝑠2𝑥. 𝑐𝑜𝑠3𝑥 − 𝑠𝑖𝑛2𝑥. 𝑠𝑖𝑛3𝑥 (2)
3.1.2 𝑠𝑖𝑛2𝑥. 𝑐𝑜𝑠𝑥 + 𝑐𝑜𝑠2𝑥. 𝑠𝑖𝑛𝑥  (2)
3.2 Determine the values of the following without using a calculator.
3.2.1 𝑠𝑖𝑛85°. 𝑐𝑜𝑠25° − 𝑐𝑜𝑠85°. 𝑠𝑖𝑛25° (3)
3.2.2 𝑐𝑜𝑠160°. 𝑐𝑜𝑠10° + 𝑠𝑖𝑛160°. 𝑠𝑖𝑛10° (4)
[11]