INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of 11 questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, etc. that you used to determine your answers.
4. Answers only will NOT necessarily be awarded full marks.
5. If necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
8. An information sheet with formulae is included at the end of the question paper.
9. Write neatly and legibly.

QUESTION 1

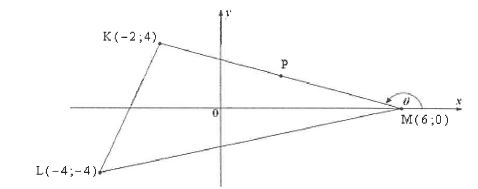
In the diagram below, A KLM with vertices K(-2; 4), L(-4;-4) and M(6; 0) is given. The angle of inclination formed by the positive x-axis and KM is 0.
P is the midpoint of KM.

Determine:
1.1 The gradient of KM (2)
1.2 θ (give your answer to the nearest degree) (2)
1.3 The coordinates of P (2)
1.4 The length of LM (in simplified surd form) (2)
1.5 The equation of the line parallel to KL passing through P in the form y= (3)
[11]

QUESTION 2

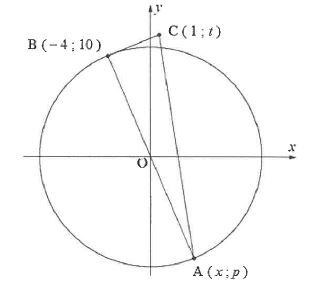
2.1 In the diagram below, O is the centre of the circle with points A(x; p) and B(-4; 10) on the circumference.
AOB is the diameter of the circle.
BC is a tangent to the circle at point B(-4; 10).
Point C(1;) is on both BC and AC.

2.1.1 Determine the equation of the circle. (2)
2.1.2 Write down the coordinates of A. (2)
2.1.3 Show that the gradient of BC is 2/5 (2)
2.1.4 Hence, determine the equation of BC in the form y=... (2)
2.1.5 Calculate the value of t. (2)

2.2 Sketch the graph defined by: 
  x² +   y² = 1
 49     4
(3)
[13]

QUESTION 3

3.1 Given: R 15,8° and K = 74,1°
Determine the following using a calculator:

3.1.1 cos R - cos 2K (2)
3.1.2 3 cosec (R/4 +84°) (3)

3.2 If sin 43° =t, express the following trigonometric ratios in terms of t:

3.2.1 cos 43° (3)
3.2.2 sec 47° (1)
3.2.3 tan 317° (3)

3.3 Solve for x:
7 cosx – tan 56 = 0 for xe[180°; 360°]
[16]

QUESTION 4

4.1 Complete: tan B- sec2 B = .... (1)
4.2 Simplify the following to one trigonometric ratio:
cos (360°+x) tan (180°+x) + cos(180° - x) sec2 (360°-x) (7)
4.3 Show that: cot (+0) sec2 0 cote-tan (4)
[12]

QUESTION 5

Given: f(x)= sin x+1 and g(x) = cos x for x [0°; 360°]
5.1 Draw sketch graphs of ƒ and g on the same set of axes on the grid provided in the ANSWER BOOK. Clearly indicate ALL turning points, end points and intercepts with the axes. (7)
5.2 Write down the range of f (2)
5.3 Write down the period of g. (1)
5.4 Determine the values of x for which:

5.4.1 g(x) f(x)= 0 for x =[180°; 360°] (2)
5.4.2 f(x).g(x) <0 (2)

[14]

QUESTION 6
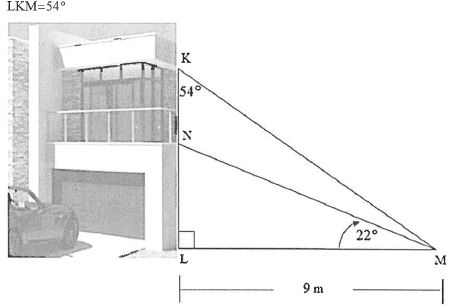
6.1 The picture and diagram below show a double-storey building with L, the foot of the building.

Two security cameras are to be installed on the side (KL) of the double-storey building at points K and N. The cameras are to focus at the gate at M, 9 m from the building. M and L lie on the same horizontal plane. The angle of elevation of N from M is 22°
LKM=54°


Determine, correct to ONE decimal place if necessary:
6.1.1 The length of LN (2)
6.1.2 KN, the distance between the two cameras (3)

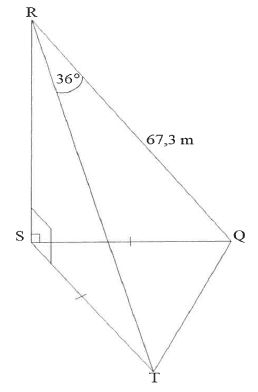
6.2 In the diagram below, RS represents a vertical tower. A man is standing on top of the tower observing two cars, T and Q.

The two cars are equidistant from S.
S, T and Q are on the same horizontal plane
TRQ = 36°
RQ = 67,3 m

Determine QT, the distance between the two cars.
(4)

[9]

QUESTION 7
7.1 Complete the following theorem:

Two tangents drawn to a circle from the same point outside the circle... (1)

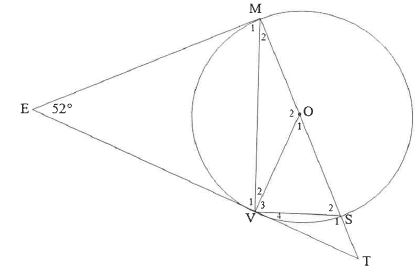
7.2 In the diagram below, O is the centre of circle MVS.

EM and EV are tangents at M and V respectively. MOS is a diameter. Tangent EV and diameter MS are produced to T.
E=52°

7.2.1 Give a reason why EMO = 90°
7.2.2 Determine, stating reasons, the size of EACH of the following angles:

1. ∧
   V₁(2)
2. ∧
   S₂(2)
3. ∧
   O₁(3)
4. ∧
   V₄(3)
5. ∧
   T

[14]

QUESTION 8

8.1 Complete the following theorem:

The exterior angle of a cyclic quadrilateral is equal to ...(1)

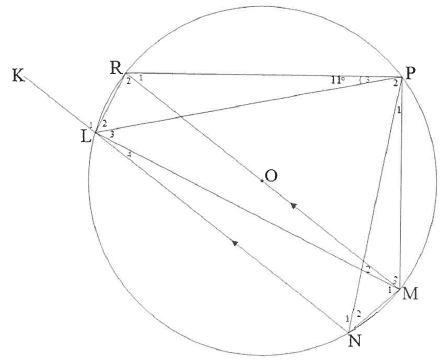
8.2 The diagram below shows a circle PRLNM with centre O. ROM is a diameter and NL is produced to K.
LN || RM
  ∧
P3 =11°

8.2.1 Give a reason why MPR=90° (1)
8.2.2 Determine, giving reasons, THREE other angles each equal to 11°. (4)
8.2.3 Give a reason why LR=NM (2)
8.2.4 Determine the size of M.. (4)
8.2.5 Determine the size of L. (2)

[14]

QUESTION 9
9.1 Complete the following theorem:

A line parallel to one side of a triangle... (1)

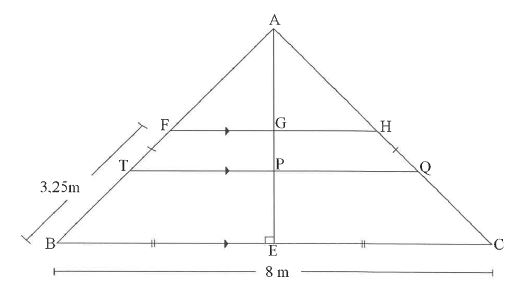
9.2 In the diagram below, AABC is drawn with AEL BC

F and T are on AB and H and Q are on AC.
FH || TQ || BC
ABAC and BE EC
BC 8 m and FB = 3,25 m
3,25m


9.2.1 Give a reason why A ABE = AACE (1)
9.2.2 Write down the length of BE. (1)
9.2.3 If it is further given that AE= 3 m and AP/AE = 2/3 determine, stating reasons:
(a) The length of AB (2)
(b) The length of AT (3)
9.2.4Hence, determine the length of FT. (3)

[11]

QUESTION 10

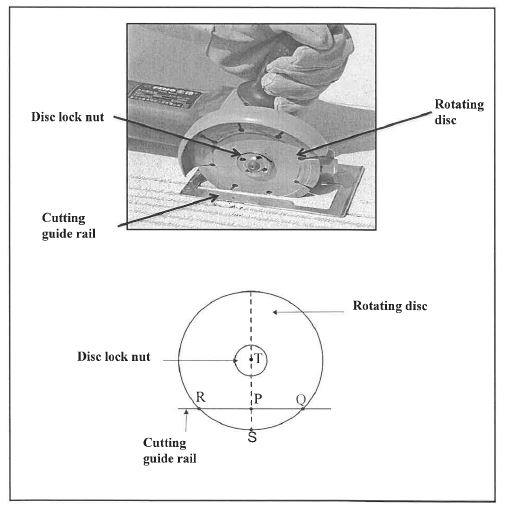
10.1 The picture below shows an angle grinder cutting through a granite slab. The diameter of the rotating disc is 115 mm and it is set at a rotational frequency of 2 700 revolutions per minute. The diagram below the picture models the situation. T is the centre of both circles which represent the rotating disc and the disc lock nut respectively.

Determine:

10.1.1 The angular velocity (in radians per second) of the rotating disc (4)
10.1.2 The length of PS (the height of the minor segment of chord RQ) if the length of chord RQ is 55 mm (round off your answer to the nearest millimetre). (4)

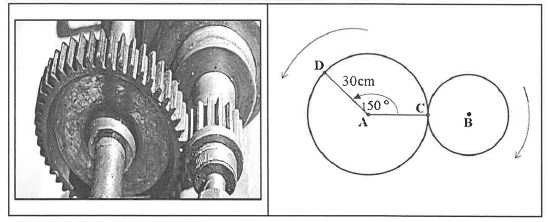
10.2 The picture below shows two gears meshed together. The diagram alongside the picture models the two meshed gears. As the larger gear (centre A), with a radius of 30 cm rotates, it causes the smaller gear (centre B) to rotate in the opposite direction. The two gears are in contact at point C after a 150° rotation of the larger gear.

10.2.1 Convert 150° to radians.(1)
10.2.2 Calculate the area of the minor sector, DAC.(3)
10.2.3 Determine the length of the minor arc, DC.(3)
10.2.4 Determine the length of the radius of the smaller gear if a 150° rotation of the larger gear causes the smaller gear to make 1- revolutions. (4)

[19]

QUESTION 11

11.1 The diagram below shows a rectangular garden with an irregularly shaded patch to be covered with grass.
Grass is sold in the form of rectangular pieces with breadth of 0,4 m and length of
2,3 m.
The straight side of the irregular patch is divided into 4 equal parts of length 0,4 m and the ordinates are 2,3 m; 1,6 m; 1,8 m; 1,4 m and 1,3 m.

11.1.1 Calculate the area of the irregular patch that must be covered with grass by using the mid-ordinate rule. (4)
11.1.2 The grass is sold at R106,80 per square metre. Determine the money that will be wasted if the cut-offs are thrown away. (4

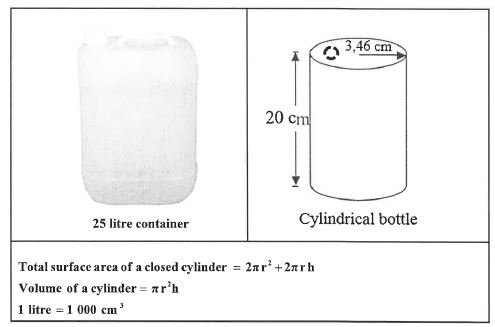
11.2 A 25 litre container of hand sanitiser is allocated to a classroom. A cylindrical bottle is then filled from this 25 litre container.

• The height of the cylindrical bottle is 20 cm and the radius is 3,46 cm.
• The cylindrical bottle has an opening at the top with a surface area of 0,45 cm².
  

11.2.1 Calculate the total surface area of the cylindrical bottle. (4)
11.2.2 If one cylindrical bottle is used until it is empty, determine how many times the bottle can be filled with sanitiser. (5)

[17]
TOTAL: 150