TECHNICAL MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupTECHNICAL MATHEMATICS PAPER 1
GRADE 12
NOVEMBER 2021
NSC EXAMINATIONS
QUESTION 1
1.1.1
2x(x + 3) = 0
x=0 or x= -3
(2)
1.1.2
x(x+9) = 12
x2 + 9x - 12 = 0
x = -b ± √b2 - 4ac
2a
= -(9) ± √(9)2 - 4(1)(-12)
2(1)
= -9±√129
2
x ≈ 1,1,8 or x ≈ -10,18
(4)
1.1.3
x(6 - x) ≥ 0
Critical values: 0 and 6
0 ≤ x ≤ 6 OR x ∈ [0;6] OR
x ≥ 0 and x ≤ 6
- both critical values
- notation/notasie A
- number line representation CA (3)
Note: Award full marks if ONLY the correct number line representation is shown.
1.2
x = 1 - 2y and 3x2 = 3 + x + y
3(1 - 2y) = 3+(1 - 2y) + y
3 - 12y + 12y2 = 4 - y
12y2 -11 - 1 = 0
(12y + 1)(y - 1) = 0 OR
y = -(11)±√(11)2 - 4(12)(-1)
2(12)
y = -1/12 -0.08 or y = 1
x = 1 -2(-1/12) or x = 1 - 2(1)
x = 7/6 ≈ 1,17 or x = -1
- substitution A
- S CA
- correct standard form CA
- factors/formula CA
- both y-values CA
- both x-values CA
OR
y = 1 - x and 3x2 = 3 + x + y
2
3x2 = 3 + x + 1 - x
2
6x2 = 6 + 2x + 1 - x
6x2 - x - 7 = 0
(6x - 7)(x + 1) = 0 OR
x = -(-1)±√(-1)2 - 4(6)(-7)
2(6)
x = 7/6 ≈ 1,17 or x = -1
y = 1 - 7/6 or y = 1-(-1)
2 2
y = -1/12 ≈ -0.08 or y = 1
- substitution A
- S CA
- correct standard form CA
- factors/form CA
- both x-values CA
- both y-valuesCA
OR
x = 1 - 2y(1) and 3x2 - 3 - x = y(2)
Sub(2) into (1)
x = 1 - 2(3x2 - 3 - x)
x = 1 - 6x2 + 6 - 2x
6x2 - x - 7 = 0
(6x - 7)(x + 1) = 0
x = 7/6 ≈ 1,17 or
x = -(-1)±√(-1)2 - 4(6)(-7)
2(6)
y = -1/12 ≈ -0.08 or y = 1
- substitution A
- S CA
- correct standard form CA
- factors/form CA
- both x-valuesCA
- both y-valuesCA
NPR
(6)
1.3.1
T = 2π√L/g
T/2π = √L/g
(T/2π)2 = (L/g)2
L = g.(T/2π)2
M squaring both sides A
L subject A
OR
T = 2π√L/g
T2 = (2π√L/g)2
T2 = 4π2L/g
L = gT2
4π2
M squaring both sides A
L subject A
(2)
1.3.2
L = g.(T/2π)2
L = 9.8.(1.74/2π)2
L = 0.75m
- SF CA
- value of L CA
OR
L = gT2
4π2
L = (9.8)(1.74)2
4π2
L = 0,75m
- SF CA
- value of L CA
OR
T = 2π√L/g
1.74 = 2π√L/9.8
L = 9.8.(1.74/2π)2
- SF A
- value of L CA
NPR NPU
(2)
1.4.1
11011002 - 111002 = 10100002
(1)
Note: No penalty if base 2 is omitted.
1.4.2
| 26 | 25 | 24 | 23 | 22 | 21 | 20 | |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | =108 |
| 1 | 1 | 1 | 0 | 0 | =28 |
= 108 - 28 = 80
- M CA
- decimal value CA
OR - M A
- decimal value CA (2)
AO: full marks
[22]
QUESTION 2
2.1.1 Non-real (1)
2.1.2 Real, rational, equal(1)
2.2
-x2 + 2qx - 4 = 0 OR x2 - 2qx + 4 = 0
b2 - 4ac < 0
(2q)2 - 4(-1)(-4) < 0 OR (-2q)2 - 4(1)(4) < 0
4q2 - 16 < 0
q2 - 4 < 0
(q - 2)(q + 2) < 0
-2 < q < 2 OR q (-2; 2) OR q > -2 and q < 2
- SF A
- end points and correct notation CA (3)
[5]
QUESTION 3
3.1.1
(81a-8) -¾
= (34a-8)-¾
= 3-3a6 OR 1/27a6 OR a6/27
Prime base or exponential property(3)
3.1.2
log216 + log34º
= log224 + log31
= 4log22 + log31
= 4(1) + 0
= 4
OR
log216 + log34º
= log224 + 0log34
= 4log22 + 0log34
= 4(1) + 0
= 4
OR
log216 + log34º
= log16 + log4º
log2 log 3
= log24 + log1
log2 log3
= 4log2 + 0
log2 log 3
= 4 + 0
= 4
(4)
3.1.3
√50x10 x √18x-4
= √900x6
= 30x3
- Product of the surds
- 30 CA
- 3 x CA
OR
√50x10 x √18x-4
= √25 x 2x10 x √9 x 2x-4
= √52x5 x 3√2x-2
= 30x3
- Product of perfect squares and prime number
- 30 CA
- 3 x CA
(3)
3.2
log3 (x + 2) = 2 +log3x
log3 (x + 2) - log3x = 2
log3x + 2 = 2
x
x + 2 = 32 OR log3x + 2 = 2log33
x x
x + 2 = 9x
x = ¼ OR x = 0.25
- log property A
- exponential CA
- S CA
- x – value CA
OR
log3 (x + 2) = 2 + log3x
log3 (x + 2) = 2log33 + log3x
log3 (x + 2) = log39 + log3x
log3 (x + 2) = log39x
x + 2 = 9x
x = ¼ OR x = 0.25
- log property A
- log property A
- S CA
- x – value CA
(4)
3.3.1
IzI = r = √x2 + y2
2√5 = √(p)2 + (4)2
20 = p2 + 16
p2 = 4 OR (p + 2)(p - 2) = 0 OR p ±√4
p = ±2
p = -2 , θ ∈(90º;180º)
(4)
3.3.2
tanθ = y/x OR cosθ = x/r
tanθ = 4/-2 OR cosθ =-2/2√5
ref .angle = 63,43º
θ =180º - 63,43º =116,57 OR 2.03rad
z = 2√5 cis 116,57º OR
z = 2√5 cis 2,03 rad
- ref. angle CA
- value of CA
- z in polar form CA
OR
sinθ = y/r
sinθ = 4/2√5
ref .angle = 63,43º
θ = 180º - 63,43 = 116,57 OR 2,03 rad
z = 2√5 cis 116,57º OR
z = 2√5 cis 2,03 rad
- ref. angle A
- value of CA
- z in polar form CA (3)
3.4
2m - ni - 6i = -3i (4i + 5)
2m - ni = 12i2 - 15i + 6i
2m - ni = 12(-1) - 9i
2m - ni =12 - 9i
2m = 12
m = 6
-ni = -9i
n = 9
- Product
- substituting i2 with – 1
- value of m
- value of n
OR
2m - ni - 6i = -3i (4i + 5)
2m - (n + 6)i = 12i2 - 15i
2m -(n + 6)i = 12(-1) - 15i
2m - (n + 6)i =12 - 15i
2m = 12
m = 6
-(n + 6)i = 15i
n = 9
- Product
- substituting i2 with – 1
- value of m
- value of n
OR
2m - ni - 6i = -3i (4i + 5)
2m - (n + 6)i = 12i2 - 15i
2m - ni - 6i = 12(-1) - 15i
2m - ni - 6i =12 - 15i
2m - 12 = ni + 6i - 15i
2m - 12 = 0 and ni-9i = 0
2m = 12
m = 6
ni = 9i
n = 9
- Product
- substituting i2 with – 1
- value of m
- value of n (4)
[25]
QUESTION 4
4.1.1
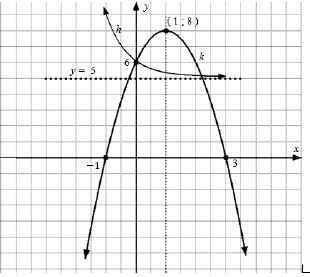
- y = 6 OR (0;6) (1)
- y = 5 (1)
- k(x) = -2x2 + 4x + 6
y-int: y = 6
x-ints..:
2x2 + 4x + 6 = 0
x2 - 2x - 3 = 0
(x + 1)(x - 3) = 0 OR x = -(-2)±√(-2)2 -4(1)(-3)
2(1)- y-int
- factors/form
- both values of x (3)
- TP
x = -b/2a = -(4)/2(-2)
=1
y = -2(1)2 + 4(1) + 6 = 8
=(1;8)
SF
x-value
y-value
OR
TP
x = -1 + 3 = 1
2
y =-2(1)2 + 4(1) + 6 = 8
= (1;8)
M
x-value
y-value
OR
k(x) = -2x2 + 4x + 6
k/(x) = -4x + 4 = 0
x = 1
y = -2(1)2 + 4(1) + 6 = 8
= (1;8)
M
x-value
y-value
OR
( -b ; 4ac - b2)
2a 4a
[ -(4) ; 4(-2)(6) - (4)2]
2(-2) 4(-2)
= (1;8)
SF A
x-value
y-value (3)
4.1.2
h :
- shape
- y- int.
- asymptote
k:
- shape
- x & y int..
- urning point(6)
4.1.3
p(x) = a/x + q and (1; 8)
q = 5
8 = a/-1 + 5
a = -3
value of q
SF
value of a (3)
4.2.1
C(5 ;0)
x-value of C
y-value at C (2)
4.2.2
D(0; -10) and B(0; -5)
BD = -5 -(-10) = 5 units
coordinates of B & D
length of BD (2)
4.2.3
f (x) = -√25 - x2 OR f (x) = -√52 - x2
equation(1)
4.2.4
3< x <5 OR x ∈( 3;5) OR x > 3 and x < 5
critical values
correct notation (2)
[24]
QUESTION 5
5.1.1
4/23 ≈ 17,39 % (1)
5.1.2
A = P(1 + in)
A = R63 150(1 + 4/23 x 7) OR R63 150 (1 + 17,39 % x 7)
= R140028, 26
≈R140022,50
OR
SI = P × i × n
= R63 150 x 4/23 x 7
OR
=R63150 x 17,39% x7
= R76 878,26
≈R76 872,50
A ≈ R63 150 + R76 878,26
OR
R63150 + R76 872,50
»R140 028,26 ≈R140 022,50
(2)
5.2
A = P(1 + i)n
R274 000 = R726 900 (1 - 15,8%)n
2 740 = (1 - 15%)n
7 269
n = log(2740/7269)
log(0.842)
n ≈ 5.67
n > 5.67 years
log form
value of (4)
5.3.1
A = P(1 + i)n
= R25 000(1 + 2,8%)4
= R27 919,81
(2)
5.3.2
Value of investment after 27 months
A = P(1 + i)n
= R15 000 (1 + 5.98%)27
12
= R17154,59482
Value of investment after 21 months
P = R17154,59482 + R6823,54 ≈ R23978, 13482
Value of investment after 7 quarters
= R23 978, 13482( 1 + 7,78%)7
4
= R27439, 55
R27439, 55 < R27 919,81
He will not have enough money
OR
27
5,98%
A =R15 000(1 + 5.98%)27 (1 + 7.78%)7
12 4
+R6 823,54( 1 + 7,78%)7
4
= R27439, 55
R27439, 55 < R27 919,81
He will not have enough money
OR
A = [R15 000 (1 + 5.98%)27 + R6 823,54 (1 + 7.78%)7]
12 4
≈ R27439, 55 < R27 919,81
He will not have enough money
Conclusion without calculation: 0 marks (6)
[15]
QUESTION 6
6.1
f(x) = -3x
f/(x) = limf(x + h) - f(x)
h
= lim -3 (x + h) - (-3x)
h
= lim -3x - 3h + 3x
h
lim -3h
h
= lim(-3)
f/(x) = -3
definition
Penalty of one mark for incorrect notation (5)
6.2.1
Dx[p3x2 - 7x + 10]
= 2p3x - 7 (2)
6.2.2
y = x - 3x2
x7
y = x-6 - 3x-5
dy/dx = -6x-7 + 15x-6
(3)
6.2.3
f(x) = 3√x2 + 5x4
f(x) = x2/3 + 5x4
f/(x) =2/3x-1/3 + 20x3 (3)
6.3.1
m = - 9
value of m (1)
6.3.2
y = x2 + 3x - 2
dy/dx = 2x + 3
2x + 3 = -9
2x = -12
x = -6
y = (-6)2 + 3(-6) - 2
y = 16
(-6 ; 16)
- derivative of y
- equat.deriv
- – 9
- value of x
- value of y (4)
6.3.3
g(x) = x2 + 3x - 2
g(x) = (-2)2 + 3(-2) -2 = -4
g(x) = (3)2 + 3(3) - 2 = 16
Ave. grad. = y2 - y1
x2 - x1
= 16 - (-4)
3-(-2)
= 20/5
= 4
both values of y
M subst. into Ave. gradient Formula/verv in gem gra
mave value
OR
Ave. grad. = g(x2) - g(x1)
x2 - x1
= [(3)2 + 3(3) - 2] - [(-2)2 + 3(-2) -2]
3-(-2)
= 16-(-4)
3-(-2)
= 20/5
= 4
OR/OF
both values of y
M subst. into Ave. gradient Formula/verv in gem gra
mave value (3)
[21]
QUESTION 7
7.1
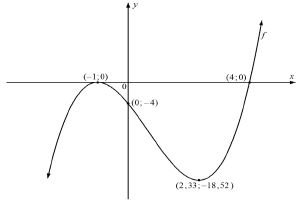
f(x) = x3 - 2x2 - 7x - 4
y = -4 OR (0;-4) (1)
7.2
f(4) = (4)3 - 2(4) - 7(4)
= 0
(x - 4) is a factor of f (x) (2)
7.3
x-intercepts; y = 0
(x - 4)(x2 + 2x + 1) = 0
( x - 4) ( x + 1) ( x + 1) = 0
x = -1 or x = 4
- quadratic factor
- factors
- x-intercepts
OR
(x + 1)(x2 - 3x - 4) = 0
( x + 1) ( x - 4) ( x + 1) = 0
x = -1 or x = 4
- quadratic factor
- factors
- x-intercepts
7.4
f/(x) = 3x2 - 4x - 7 = 0
(3x - 7)(x + 1) = 0 OR x = -(-4)±√(-4)2 -4(3)(-7)
2(3)
x = 7/3 or x = -1
f(7/3) = (7/3)3 - 2(7/3)2 - 7(7/3) - 4 = -500/27 ≈ -18.52
(7/3 ; -500/27) and(-1 ; 0)
- derivative
- quating derivative to 0
- factors/formula
- both values of x
- both values of y (5)
7.5
- shape
- y-intercept
- both x-intercepts
- both turning points(4)
AO: Full marks/Volpunte
7.6
-1 < x < 7/3 OR -1 < x < 2,33
crit. values
correct notation
OR
x ∈ (-1 ; 7/3) OR x ∈ (-1 ; 2,33)
crit. values
correct notation
OR
x > -1 and x < 7/3 OR x > -1 and x < 2,33
crit. values
correct notation(2 )
[17]
QUESTION 8
8.1
V = l x b x h
4000 = x2h 2
∴ h = 4000
x2
✔ SF A (1)
8.2
Tot. Surface Area = length × breadth + 2 × length × height +2 × breadth × height
Tot .Surface Area = x2 + 2xh + 2xh
x2 + 4x (4000/x2)
= x2 + 16 000
x
OR/OF
∴ Tot. Surface Area = Area of base + (perimeter of base × height)
Tot. Surface Area = x2 + 4xh
x2 + 4x (4000/x2)
x2 + 16 000 =
x
8.3
∴ Tot = x2 + 16 000
x
= x2 + 16 000x-1
d(Surface Area) = 2x - 16000x-2
dx
= 2x - 16000
x2
2x3 - 16000 = 0
x3 = 8000
x = 20cm
h = 4000 = 10
(20)2
QUESTION 9
9.1.1
∫x (x2 x 6x)dx
= ∫(x3 + 6x2 )dx
= x4/4 + 2x3 + C
✔ S A
✔
(4)
9.1.2
∫ (3x + 1/x)dx
= 3x /ln3 + ln x + C
9.2
A = ∫4k g(x)dx
= ∫4k 3x2 dx
= x3]4k
= (4)3 - (k)3
∴(4)3 - (k)3 = 56
∴k3 = 8
∴k= 2
OR
A= ∫410 g(x)dx
= ∫410 3x2 dx
= x3]40
= (4)3 - (0)3 = 64
A = ∫20 g(x)dx
= x3]20
= (2)3 - (0)3 =8
∴ 64 - 8 = 56
∴ k= 2
OR
Trial & Error Method
A= ∫4k g(x)dx
= ∫4k 3x2 dx
= x3]4k
Let k = 1
= x3]41
= (4)3 - (1)3
= 63
Let k = 2
= x3]42
=(4)3 - (2)3
= 56
∴ k = 2
[13]
TOTAL/TOTAAL: 150