INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of NINE questions.
2. Answer ALL the questions.
3. Answer QUESTIONS 4.1.2 and 7.5 on the ANSWER SHEETS provided. Write your centre number and examination number in the spaces provided on the ANSWER SHEETS and hand in the ANSWER SHEETS with your ANSWER BOOK.
4. Number the answers correctly according to the numbering system used in this question paper.
5. Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
6. Answers only will NOT necessarily be awarded full marks.
7. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
8. If necessary, round off answers to TWO decimal places, unless stated otherwise.
9. Diagrams are NOT necessarily drawn to scale.
10. An information sheet with formulae is included at the end of the question paper.
11. Write neatly and legibly.

QUESTION 1

1.1 Solve for x:

1.1.1 2x(x+3)=0
1.1.2 x(x+9)=12 (correct to TWO decimal places) (4)
1.1.3 x(6-x)≥ 0 and then represent the solution on a number line (3)

1.2 Solve for x and y if:

x=1-2y and 3x²=3+x+y

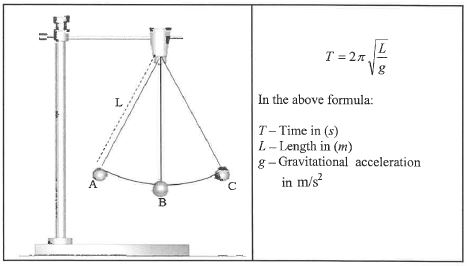
1.3 The diagram below shows a simple pendulum swinging from point A to point C. Alongside the picture is the formula for calculating the time (7) taken for the pendulum to swing from point A to point C, where (L) represents the length of the string and (g) the gravitational acceleration.

1.3.1 Make L the subject of the formula. (2)
1.3.2 Hence, calculate the numerical value of L if g=9,8 m/s² and the time taken T = 1,74s (2)

1.4 Given binary numbers:

A=1101100, and B = 11100,

1.4.1 Evaluate AB (leave your answer in binary form). (1)
1.4.2 Hence, convert your answer in QUESTION 1.4.1 to a decimal number. (2)

[22]

QUESTION 2

2.1 Given the roots: x=5±√k-9

Describe the nature of the roots if:
2.1.1 k<9 (1)
2.1.2 k=9 (1)

2.2 Determine the value(s) of q for which the equation -x² + 2qx - 4=0 will have non-real roots. (3)

[5]

QUESTION 3

3.1 Simplify the following WITHOUT using a calculator:

3.1.1 (8la^-8)^-¾  (3)
3.1.2 log₂ 16+ log₃ 4° (4)
3.1.3 √50x¹⁰ x √18x^-4 (3)

3.2 Solve for x: log, (x+2)=2 + log₃ x (4)

3.3 Given the complex number z=p+4i with the modulus 2√5 and the argument θ ∈ (90°: 180°)
0 = (90°; 180°)

3.3.1  Determine the value of p. (4)
3.3.2 Hence, express z in the polar form z  = r cis 0 (3)

3.4 Solve for m and n if 2m-ni-6i--3i (4i+5). (4)
[25]

QUESTION 4
4.1 Given: h(x)= +5 and k(x) = -2x2+4x+6
4.1.1 Determine:

1. The y-intercept of h (1)
2. The equation of the asymptote of h (1)
3. The x- and y-intercept(s) of k (3)
4. The turning point of k (3)

4.1.2 Hence, sketch the graphs of h and k on the same set of axes on the ANSWER SHEET provided. Clearly show the intercepts with the axes, turning points and any asymptote(s). (6)
4.1.3  If p(x)= a/x + q, determine the numerical value of a if p is the graph passing through (-1; 8) and has the same horizontal asymptote as h. (3)

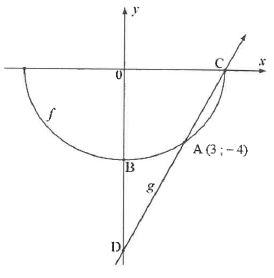
4.2 Sketched below are the graphs of ƒ and g defined by f(x)=-√(r² - x²) and g(x)=2x-10 respectively.

A(3; -4) and C are the points of intersection of ƒ and g.
B and D are the y-intercepts of ƒ and g respectively.

Determine:

4.2.1 The coordinates of C (2)
4.2.2 The length of DB (2)
4.2.3 The equation of ƒ (1)
4.2.4 The value(s) of x for which g(x)-f(x)>0 (2)
[24]

QUESTION 5

5.1 An electrician purchased equipment worth R63 150 and was charged a simple interest rate of ⁴/₂₃ on the purchase amount each year. He will repay the equipment over a period of 7 years.
5.1.1 Express ⁴/₂₃ in percentage. (1)
5.1.2 Determine the total payment at the end of the 7^th year. (2)

5.2 A newly bought machine, costing R726 900, depreciates at a rate of 15,8% per annum according to the reducing-balance method.
 

Determine the number of years (n) it will take for the value of the machine to be less than R274 000.

5.3 Four years ago, Sizwe opened a savings account to pay for his studies at a technical college.

• He immediately made a deposit of R15 000 into the account at an interest rate of 5,98% p.a., compounded monthly.
• At the end of 27 months, he added R6 823,54 to the same account and the interest rate then changed to 7,78% per annum, compounded quarterly.
• The year when he started his savings, the fees at the college were R25 000 for the course. The fees increased at a compound rate of 2,8% per annum.

5.3.1 Determine the college fees at the end of the 4th year, if the fees continue to increase at the same rate.(2)
5.3.2 Determine whether Sizwe would have saved enough money to pay for the fees at the end of the 4-year investment period. (6)

[15]

QUESTION 6

6.1 Determine f'(x) using FIRST PRINCIPLES if f(x)=-3x (5)
6.2 Determine:

6.2.1 D_x[p³x² - 7x + 10] (2)
6.2.2 dy/dx if y= x - 3x²   (3)
                             x⁷
6.2.3 f'(x) if f(x)= ³√x² +5x⁴ (3)

6.3 The equation of the tangent defined by f(x)=mx+c to the curve g(x) = x² + 3x-2, is perpendicular to the line p(x) = ¹/₉x - 4

6.3.1 Write down the value of m. (1)
6.3.2 Hence, determine the coordinates of the point of contact of the tangent to the curve g. (4)
6.3.3 Determine the average gradient of g between the points where x=3 and x = -2. (3)

[21]

QUESTION 7

Given: f(x)= x³ - 2x² - 7x - 4

7.1 Write down the y-intercept of f (1)
7.2 Show that x-4 is a factor of f. (2)
7.3 Determine the x-intercepts of f (3)
7.4 Determine the coordinates of the turning points of f (5)
7.5 Sketch the graph of ƒ on the ANSWER SHEET provided. Clearly show ALL the intercepts with the axes and the turning points. (4)
7.6 Determine the value(s) of x for which the graph of ƒ is decreasing. (2)

[17]

QUESTION 8

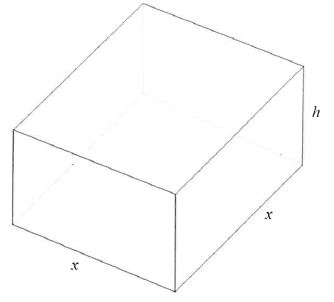
A steel manufacturing company wants to manufacture an open square-based stainless steel container with a volume of 4 000 cm3.
The dimensions of the square-based container will be length = x cm, width= x cm and height = h cm.

8.1 Show that the height of the container can be expressed as: h=4000
8.2 Hence, show that the surface area of the container can be expressed as:

Surface area = x²  +  16 000
                                        x

8.3 Determine the numerical value of the height of the container if the surface area is minimised. (1) [8]

QUESTION 9

9.1 Determine the following integrals:

9.1.1 ∫x(x² + 6x) dx} (4)
9.1.2 √(3^x + 1/x)dx

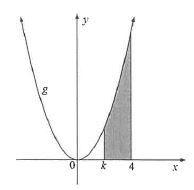
9.2 The sketch below represents the area bounded by the function g defined by g(x)=3x² and the points where x=k and x=4. (2)

Determine the value of k if the bounded area is 56 square units. (7)

[13]

TOTAL: 150

INFORMATION SHEET: TECHNICAL MATHEMATICS