MATHEMATICAL LITERACY PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY PAPER 2
GRADE 12
NSC EXAMINATIONS
NOVEMBER 2021
QUESTION 1
1.1 Gadibolae bought Pringles (chips in a cylindrical container) on promotion at a shop. The promotion advertisement is shown below, together with a diagram of the Pringles container with dimensions.
| PROMOTION ADVERTISEMENT FOR PRINGLES | DIMENSIONS OF THE CYLINDRICAL PRINGLES CONTAINER |
 Promotion available: From 11 Jan. 2021 to 31 Mar. 2021 | 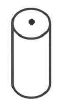 Diameter = 64 mm Height = 230 mm |
Use the information above to answer the questions that follow.
1.1.1 Determine (in grams) the total mass of the Pringles promotion bought for R100.
1.1.2 Write down the radius of a single Pringles container.
1.1.3 Choose the letter of the answer that will make the following statement TRUE.
The unit to calculate the inner volume of a Pringles container is:
- mm3
- mm2
- 64 x 23mm2
1.1.4 Determine the total number of days this promotion is available.
1.1.5 Calculate the price of two 110 g Pringles containers in this promotion.
1.2 Paul has entered a motorcycle race. The digital clock in QUESTION 1.2.1 shows the time he finished the race.
The odometer in QUESTION 1.2.2 shows the reading as the motorcycle crossed the finishing line.
Choose an item from COLUMN B to complete the statements in COLUMN A. Write only the letter (A-E) next to the question numbers (1.2.1 and 1.2.2), e.g. 1.2.3 F.
| COLUMN A | COLUMN B |
1.2.1 The analogue clock that shows the same time as the digital clock below, is ... | |
| 1.2.2 Given the following odometer: Paul's speed is ...  |
|
1.3 A wooden L-shaped flower bed is filled with soil. Below is the L-shaped flower bed with dimensions, with D as a missing length.
| DIMENSIONS OF THE L-SHAPED FLOWER BED | PICTURE:L-SHAPED FLOWER BED |
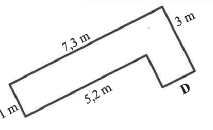 |  |
NOTE: All corners are right angles.
Use the information above to answer the questions that follow.
1.3.1 Convert the longest dimension of the L-shaped flower bed to cm.
1.3.2 Calculate the missing length, D.
1.3.3 The volume of the flower bed with materials can be calculated as follows:
Volume = (2,1m x 3m x 0,5 m) + (5,2m x 1m x 0,5 m)
= 3,15 m3 +2,6m3 - 5,75m3
State which value in the above calculation represents the height of the flower bed.
1.4 Below is the layout plan of the inside cabin of a small aeroplane. All the passenger seats face the front except the seat of the airhostess. On all flights there will be an airhostess.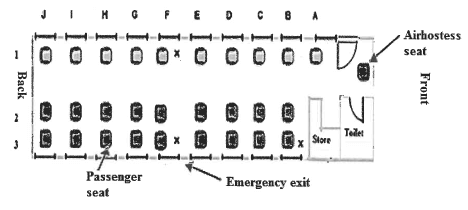
Use the information above to answer the questions that follow,
1.4.1 Explain the meaning of a layout plan.
1.4.2 Calculate the maximum number of passenger seats available in this aeroplane.
1.4.3 Stofile is seated in Dl. He gets out of his seat and walks past his seat and two more seats towards the back to talk to his friend who is seated on Stofile's right-hand side.
Using the same notation as Stofile's seat, write down the seat number of his friend. (2)
1.4.4 During the flight, passengers are allowed to choose a light snack and a drink. The choices are as follows: a muffin or a sandwich with a cola, a juice or bottled water.
Write down the number of options they can choose from.
QUESTION 2
ANNEXURE A shows the floor plan of Jan's house, with a veranda*, in South Africa,
A veranda, also known as a porch or 'stoep', is an open area with a roof over it.
The following is an artist's drawing of one of the elevations of Jan's house.
Use ANNEXURE A and the information above to answer the questions that follow.
2.1 Write down the number of bedrooms on the floor plan.
2.2 Which room will be the first room you will enter from the veranda?
2.3 In which general direction does the master bedroom window face?
2.4 One of the door locks needs to be changed.
Write down the probability, in simplified fractional form, that it is NOT one of the interior doors.
2.5 Jan remarked that the kitchen gets a lot of sunlight.
Critically comment on his remark.
2.6 Give ONE reason why the windows shown in the above drawing do NOT represent the windows of the kitchen and the dining room.
2.7 The scale used for the floor plan is 1 cm representing 1 000 mm in real life.
2.7.1 Write the given scale in number scale format.
2.7.2 Measure the inner length of bedroom 2 and use the given scale to calculate the actual length (in m) of bedroom 2.
2.7.3 Jan stated that the given scale is NOT very accurate to use if photocopies were going to be made of the plan.
Critically comment on his statement and give a reason for your answer. (24)
QUESTION 3
Tsidi needs a bookshelf to store her files. She decides to buy a second-hand wooden bookshelf with two shelves, as illustrated below.
Top Shelf
DIMENSIONS:
Inside width 162 cm
Total outside height 80 cm
Inside height of the bottom shelf 40 cm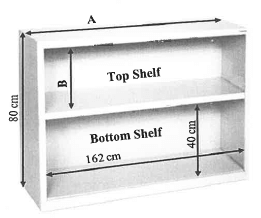
NOTE: Area of a rectangle = length x width
Use the information above to answer the questions that follow.
3.1 The top shelf has a thickness of 1,5 cm all around.
3.1.1 Determine A, the outside length of the bookshelf.
3.1.2 The base of the bottom shelf is 4,5 cm thick.
Determine B, the inside height of the top shelf.
3.2 The total outside height of the bookshelf is 31,496 inches.
Determine (rounded to TWO decimal places) the conversion factor for the height in the form 1 inch = ... cm.
3.3 Tsidi bought the bookshelf at a discounted price because the backboard which covers the entire width and height of the bookshelf, needed painting. She decides to do the following:
- Remove the backboard.
- Paint the back of the backboard with a single coat of paint.
- Paint the front of the backboard with two coats of paint.
- Nail the backboard to the bookshelf.
3.3.1 Calculate (in cm) the area of one side of the backboard.
3.3.2 Convert the answer in QUESTION 3.3.1 to m’
3.3.3 One litre of paint covers 6,9 m2
Determine (rounded to TWO decimal places) the number of litres of paint required to paint the backboard completely.
3.3.4 Tsidi stated that one 500 ml can of paint is sufficient to paint the backboard completely.
Verify, with calculations, whether her statement is valid.
3.4 Tsidi wants to organise her documents in files. She was informed that you can store files separately (single files) or in a filing box as shown in the picture below.
PICTURE OF A FILING BOX WITH FILES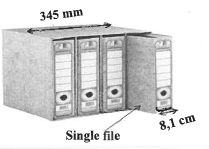 | MEASUREMENTS A single file has a width of 8,1 cm. The width of the filing box is 345 mm |
Use the information above to answer the following questions.
3.4.1 Determine the maximum number of filing boxes that could fit on one shelf, which is 162 cm wide.
3.4.2 Calculate the difference in the number of files that she can place on one shelf if she packs the shelf with single files rather than the filing boxes.
3.4.3 Give a possible reason why Tsidi would prefer the filing boxes.
3.4.4 Tsidi bought filing boxes to pack the top shelf completely. She could not remember in which file she placed a document. She randomly chooses one of the files out of the filing boxes. Determine, as a percentage to TWO decimal places, the probability that the file she chooses will contain the document she is looking for.
[35]
QUESTION 4
4.1 Mr Venter bought a farm in order to sell chickens and vegetables. On ANNEXURE B is the layout plan of the farmyard.
Use ANNEXURE B to answer the questions that follow.
4.1.1 Name the feature on the layout plan which has an irregular shape.
4.1.2 The letter J on the map represents Jojo tanks.
Give a reason why it is important to have a water tank at one's house.
4.1.3 Jojo tanks are usually filled with rainwater. Write down TWO structures where the water to fill a Jojo tank could possibly come from.
4.1.4 Calculate (in m?) the area of the garden expansion. You may use the following formula: Area of a triangle =½ x base x height
4.1.5 Mr Venter decides to replace the fence around the circular chicken site. The circumference of the circular site is 18,852 m.
| TWO COST OPTIONS FOR THE WIRE MESH | |
| OPTION A R1 154 for a 10 m roll | OPTION B R127,30 per running metre |
Picture of wire mesh | |
By means of calculations, advise Mr Venter which option is more economical. (5)
4.2 One of the Jojo tanks on his farm has a 5 000 t capacity. The height of the tank is 220 cm.
NOTE: 1 000 cm = 14
Calculate (in cm) the radius of the tank.
You may use the following formula: Volume of a cylindrical tank = 3,142 x (radius)2 x height
4.3 Mr Venter bought a chair which still has to be assembled. Below is a picture of the assembled chair showing different parts with some dimensions (in inches).
Picture of assembled chair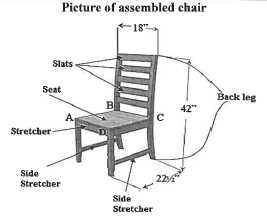
NOTE: 18" = 18 inches
Use the information above to answer the questions that follow,
4.3.1 Write the following as a simplified ratio:
Width of the chair : height of the chair
4.3.2 Convert the height of the chair to mm.
You may use the following conversions: 1 000 mm= 3,28084 feet and 12 inches = 1 foot
4.3.3 ANNEXURE C shows pictures and written instructions for the first steps to assemble the chair. Choose an assembly instruction from COLUMN B that matches a picture in COLUMN A. Write only the letter ((i) to (iii)) next to the question numbers (4.3.3(a) to 4.3.3c)) in the ANSWER BOOK.
4.3.4 State whether Por Q represents the side stretcher.![]()
4.3.5 The seat is shown in the sketch below.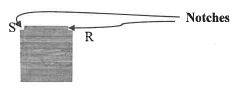 Describe how you would position the seat so that it is attached to the rest of the structure. (Use the given letters A, B, C, D on the picture and S, R on the sketch). (3)
Describe how you would position the seat so that it is attached to the rest of the structure. (Use the given letters A, B, C, D on the picture and S, R on the sketch). (3)
[33]
QUESTION 5
5.1 Noah is a travelling salesman who lives in the United States of America (USA). He uses a map to estimate his travelling time between cities.
On ANNEXURE D is a partial map which shows the following:
- Various cities
- Distances in miles) between cities
- Average travelling times (in hours and minutes) between these cities
Use ANNEXURE D to answer the questions that follow.
5.1.1 Choose ONE letter (W, X, Y or 2) that will make EACH of the following statements below TRUE.
The average time (in hours) to travel between Lee and Springfield
W 50/100
X 50/100
Y 0,5
Z 41
Which city lies southeast of Boston?
W Providence
X Lowell
Y Gloucester
Z Plymouth
5.1.2 Noah found that the same time 01:05 is estimated for travelling from Providence to Boston and from Springfield to Worcester.
- Write down the actual distances (in miles) from Providence to Boston and from Springfield to Worcester.
- Give ONE possible reason why the map indicates the same travelling time for these two different distances.
5.1.3 Noah travelled from Portland passing three cities (A, B and C in the table) to reach his destination city, D.
TABLE 1 below shows the time taken to travel between various unknown cities indicated by A, B, C and D.
TABLE 1: TIME TAKEN BETWEEN CITIES
| START CITY | DESTINATION CITY | TIME TAKEN BETWEEN CITIES |
| Portland | A | 01:35 |
| A | B | ½ hour |
| B | C | 00:35 |
| C | D | 1 hour |
Name cities A, B, C and D.
5.1.4 The fuel tank of Noah's car has a capacity of 23 gallons. Noah claims that in South Africa it will cost him less than R1 400 to fill up his fuel tank to capacity.
NOTE:
- 1 gallon= 3,785 litres
- Fuel cost R15,977 €
Verify, with calculations, whether his claim is valid,
5.1.5 Noah stays in Greenfield and travels to Fitchburg and back, from Monday to Friday. He fills his car's fuel tank on Monday morning. The fuel consumption of his car is 18 miles per gallon. He refuels his car to capacity as soon as he does not have enough fuel to complete a trip between the two cities.
Determine the number of gallons of fuel left in his car's tank on arrival in Greenfield on Friday afternoon.
(8)
5.2 A temperature reading of -7°C was displayed on the screen on the dashboard of Noah's car. Determine (to the nearest ten) the temperature in degrees Fahrenheit.
Use the formula: 'C = 5/9 x ('F-32)
[29]
TOTAL: 150

