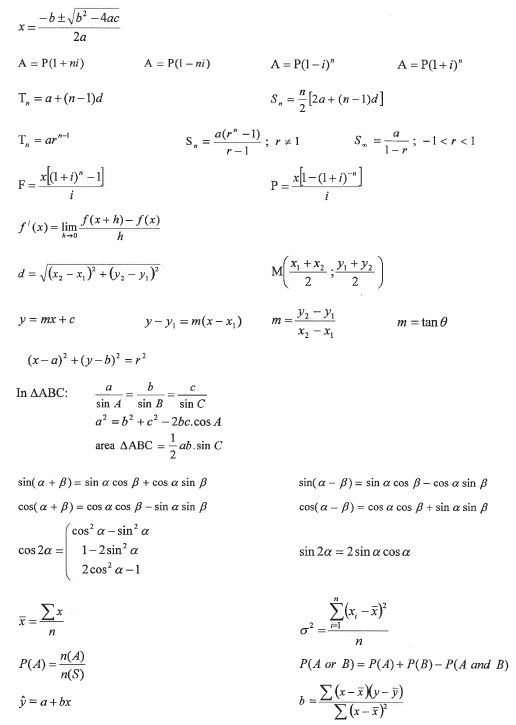MATHEMATICS PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 2
GRADE 12
NSC PAST PAPERS AND MEMOS
NOVEMBER 2021
QUESTION 1
A bakery kept a record of the number of loaves of bread a tuck-shop ordered daily over the last 18 days. The information is shown in the table below.
| 10 | 11 | 13 | 14 | 14 | 15 | 16 | 18 | 18 |
| 19 | 19 | 20 | 21 | 35 | 35 | 37 | 40 | 41 |
Calculate the:
1.1.1 Mean number of loaves of bread ordered daily
1.1.2 Standard deviation of the data
1.1.3 Number of days on which the number of loaves of bread ordered was more than one standard deviation above the mean
1.2 The tuck-shop owner was not able to sell all the loaves of bread delivered daily. He calculated the mean number of loaves sold over the 18 days to be 20. Calculate the number of loaves of bread which were NOT sold over the 18 days.
1.3 One of the two box and whisker diagrams drawn below represents the data given in the table above.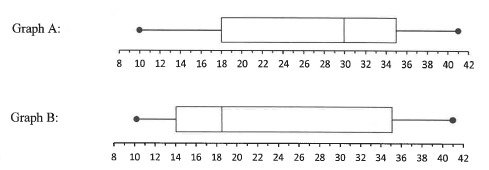
1.3.1 Which ONE of the two box and whisker diagrams, drawn above, correctly represents the data? Write down a reason for your answer. (2)
1.3.2 Describe the skewness of the data.
[10]
QUESTION 2
A farm stall sells milk in 5-litre containers to the local community. The price varies according to the availability of milk at the farm stall. The price of milk, in rands per 5-litre container, and the number of 5-litre containers of milk sold, are recorded in the table below.
| Price of milk in rands per 5-litre container (x) | 26 | 32 | 36 | 28 | 40 | 33 | 29 | 34 | 27 | 30 |
| Number of 5-litre containers of milk sold | 48 | 30 | 26 | 44 | 23 | 32 | 39 | 29 | 42 | 33 |
2.1 On the grid provided in the ANSWER BOOK, draw the scatter plot to represent the data.
2.2 Determine the equation of the least squares regression line for the data.
2.3 If the farmer sells a 5-litre container of milk for R38, predict the number of 5-litre containers of milk he will sell.
2.4 Refer to the correlation between the price of 5-litre containers of milk and the number of 5-litre containers of milk sold, and comment on the accuracy of your answer to QUESTION 2.3.
[10]
QUESTION 3
In the diagram, A(-2; 10), B(k; k) and C(4 ; -2) are the vertices of AABC. Line BC is produced to H and cuts the x-axis at E(12;0). AB and AC intersects the x-axis at F and G respectively. The angle of inclination of line AB is 81,87º.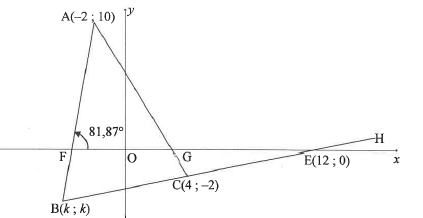
3.1 Calculate the gradient of:
3.1.1 BE
3.1.2 AB
3.2 Determine the equation of BE in the form y = mx + c
3.3 Calculate the:
3.3.1 Coordinates of B, where k<0
3.3.2 Size of A
3.3.3 Coordinates of the point of intersection of the diagonals of parallelogram ACES, where S is a point in the first quadrant
3.4 Another point T(p:p), where p>0, is plotted such that ET-BE-417 units.
3.4.1 Calculate the coordinates of T.
3.4.2 Determine the equation of the:
- Circle with centre at E and passing through B and T in the form (x -a)2 +(y-b)2 = r2
- Tangent to the circle at point B(k; k)
QUESTION 4
In the diagram, the circle centred at N(-1; 3) passes through A(-1,-1) and C. B(4:2), C, D and E are joined to form a parallelogram such that BE is parallel to the x-axis. CD is a tangent to the circle at C and CD=6 units.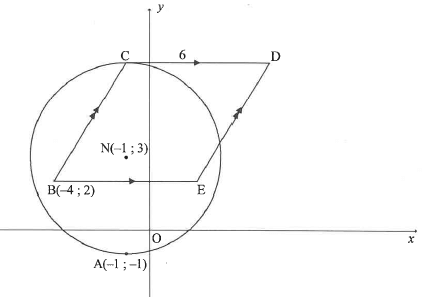
4.1 Write down the length of the radius of the circle.
4.2 Calculate the:
4.2.1 Coordinates of C
4.2.2 Coordinates of D
4.2.3 Area of ABCD
4.3 The circle, centred at N, is reflected about the line y x. M is the centre of the new circle which is formed. The two circles intersect at A and F.
Calculate the:
4.3.1 Length of NM
4.3.2 Midpoint of AF
QUESTION 5
5.1 Without using a calculator, simplify the following expression to ONE trigonometric ratio:
sin 140°.sin(360° - x)
cos 50°. tan(-x)
5.2 Prove the identity: - 2 sin* x + cos x +1 = 2cosx-1
1- cos(540° - x)
5.3 Given: sin 36° = √1-p2
Without using a calculator, determine EACH of the following in terms of p:
5.3.1 tan 36°
5.3.2 cos108°
QUESTION 6
6.1 Given: cos(a - β) = cos a cos + sin a sin β
6.1.1 Use the given identity to derive a formula for cos(a+β)
6.1.2 Simplify completely: 2cosbxcos 4x - cos 10x + 2sin2x
6.2 Determine the general solution of tan x = 2 sin 2x where cos x<0.
QUESTION 7
In the diagram below, the graph of f(x) = -2 sinx is drawn for the interval X∈ [-180° ; 180°).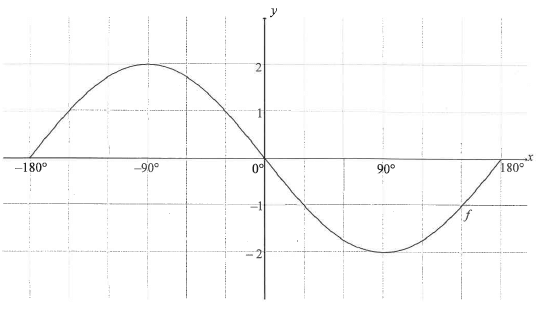
7.1 On the grid provided in the ANSWER BOOK, draw the graph of g(x) = cos(x - 60°) for x ∈ (-180°; 180°). Clearly show ALL intercepts with the axes and turning points of the graph.
7.2 Write down the period of f(3x).
73. Use the graphs to determine the value of x in the interval x ∈ [-180° ; 180°] for which f(x)-g(x)=1.
7.4 Write down the range of k, if k = ½g(x) + 1
QUESTION 8
In the diagram below, T is a hook on the ceiling of an art gallery. Points , S and R are on the same horizontal plane from where three people are observing the hook T. The angle of elevation from Q to T is x.
QSR = 90° + x, QRS = x, QR = 5 units and TS=SQ.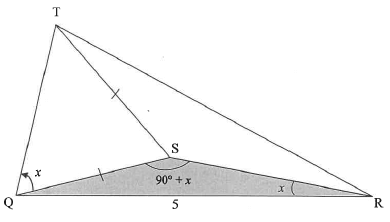
8.1 Prove that QS - 5 tan x
8.2 Prove that the length of QT=10 sinx
8.3 Calculate the area of ATQR if TOR = 70° and x=25°.
QUESTION 9
In the diagram, PQRS is a cyclic quadrilateral. PS is produced to W. TR and TS are tangents to the circle at R and S respectively. T=78° and =93°.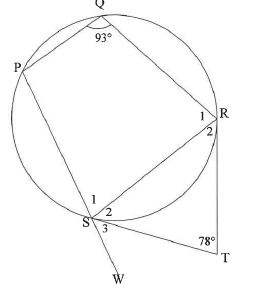
9.1 Give a reason why ST = TR.
9.2 Calculate, giving reasons, the size of:
9.2.1 S2
9.2.2 S3
QUESTION 10
In the diagram, BE and CD are diameters of a circle having M as centre. Chord AE is drawn to cut CD at F. AEI CD. Let C=x.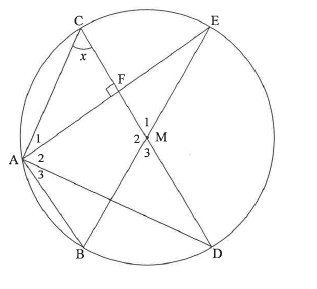
10.1 Give a reason why AF= FE.
10.2 Determine, giving reasons, the size of M1 in terms of x.
10.3 Prove, giving reasons, that AD is a tangent to the circle passing through A, C and F.
10.4 Given that CF = 6 units and AB = 24 units, calculate, giving reasons, the length of AE.
QUESTION 11
11.1 In the diagram, chords DE, EF and DF are drawn in the circle with centre O. KFC is a tangent to the circle at F.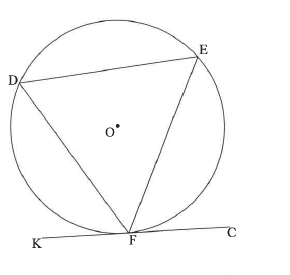
Prove the theorem which states that DFK = Ê.
11.2 In the diagram, PK is a tangent to the circle at K. Chord LS is produced to P. N and M are points on KP and SP respectively such that MN | SK. Chord KS and LN intersect at T.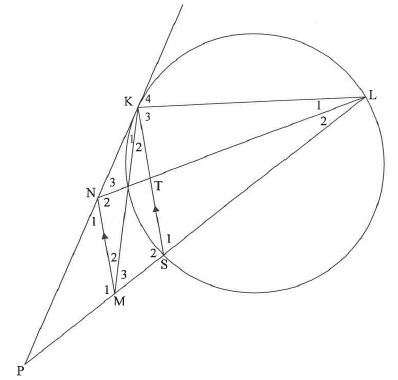
11.2.1 Prove, giving reasons, that:
- K4 = NML
- KLMN is a cyclic quadrilateral
11.2.2 Prove, giving reasons, that ALKN | AKSM.
11.2.3 If LK = 12 units and 3KN = 4SM, determine the length of KS.
11.2.4 If it is further given that NL = 16 units, LS - 13 units and KN - 8 units, determine, with reasons, the length of LT.
TOTAL: 150
INFORMATION SHEET