MATHEMATICS PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
GRADE 12
NSC EXAMINATIONS
NOVEMBER 2021
QUESTION 1
1.1 Solve forx:
1.1.1 x2 - 2x - 24 = 0
1.1.2 2x2 - 3x - 3 = 0 (correct to TWO decimal places)
1.1.3 x2 + 5x ≤ - 4
1.1.4 √x + 28 = 2 - x
1.2 Solve simultaneously for x and y in: 2y = 3 + x and 2xy +7= x2 +4y2
1.3 The roots of an equation are
x = - n ±√n2 - 4mp
2m
where m, n and p are positive real numbers. The numbers m, n and p, in that order, form a geometric sequence. Prove that x is a non-real number.
QUESTION 2
Given the geometric series: X+ 90 + 81 +...
2.1 Calculate the value of x.
2.2 Show that the sum of the first n terms is S. = 1 000(1-(0.9)n).
2.3 Hence, or otherwise, calculate the sum to infinity
QUESTION 3
Consider the quadratic number pattern: -145; -122 ;-101 ;...
3.1 Write down the value of T4
3.2 Show that the general term of this number pattern is Tn = -n2 +26n - 170
Between which TWO terms of the quadratic number pattern will there be a difference of -121?
3.4 What value must be added to each term in the number pattern so that the value of the maximum term in the new number pattern formed will be 1?
QUESTION 4
Consider the linear pattern: 5:7:9;...
4.1 Determine T51
4.2 Calculate the sum of the first 51 terms.
4.3 Write down the expansion of ![]() . Show only the first 3 terms and the last term of the expansion.
. Show only the first 3 terms and the last term of the expansion.
4.4 Hence, or otherwise, calculate ![]() . ALL working details must be shown.
. ALL working details must be shown.
QUESTION 5
Given: f(x) = -1/x-3 +2
5.1 Write down the equations of the asymptotes of f.
5.2 Write down the domain of f.
5.3 Determine the coordinates of the x-intercept of f.
5.4 Write down the coordinates of the y-intercept of f.
5.5Draw the graph of f. Clearly show ALL the asymptotes and intercepts with the axes.
QUESTION 6
The graph of f(x) = log4x is drawn below. B(k; 2) is a point on f.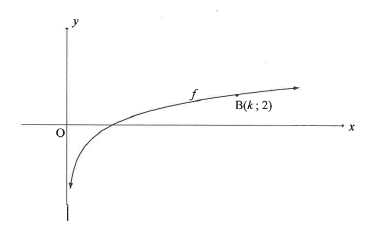
6.1 Calculate the value of k.
6.2 Determine the values of x for which -15 f(x) < 2.
6.3 Write down the equation of f -1, the inverse off, in the form y=...
6.4 For which values of x will x.f -1(x) <0?
QUESTION 7
The graph of f(x) = (x+4)(x-6) is drawn below.
The parabola cuts the x-axis at B and D and the y-axis at G.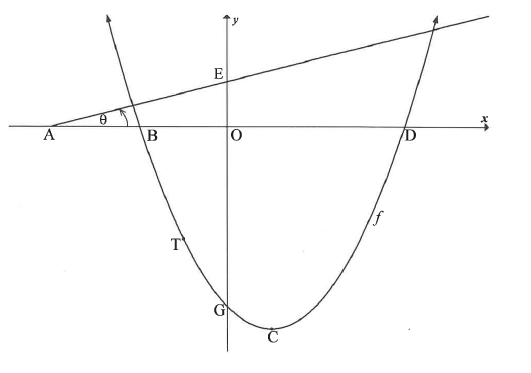
C is the turning point of f.
Line AE has an angle of inclination of θ and cuts the x-axis and y-axis at A and E respectively.
T is a point on f between B and G.
7.1 Write down the coordinates of B and D.
7.2 Calculate the coordinates of C.
7.3 Write down the range of f.
7.4 Given that θ =14,04º and the tangent to f at T is perpendicular to AE.
7.4.1 Calculate the gradient of AE, correct to TWO decimal places.
7.4.2 Calculate the coordinates of T.
7.5 A straight line, 8, parallel to AE, cuts f at K(-3; -9) and R. Calculate the x-coordinate of R.
QUESTION 8
8.1 A farmer bought a tractor for R980 000. The value of the tractor depreciates annually at a rate of 9,2% p.a. on the reducing-balance method. Calculate the book value of the tractor after 7 years.
8.2 How many years will it take for an amount of R75 000 to accrue to R116 253,50 in an account earning interest of 6,8% p.a., compounded quarterly?
8.3 Thabo wanted to save R450 000 as a deposit to buy a house on 30 June 2018.
8.3.1 He deposited a fixed amount of money at the end of every month into an account earning interest of 8,35% p.a., compounded monthly. His first deposit was made on 31 July 2013 and his 60th deposit on 30 June 2018. Calculate the amount he deposited monthly. (3)
8.3.2 Thabo bought a house costing R1 500 000 and used his savings as the deposit. He obtained a home loan for the balance of the purchase price at an interest of 12% p.a., compounded monthly over 25 years. He made his first monthly instalment of R11 058,85 towards the loan on 31 July 2018.
- What will the balance outstanding on the loan be on 30 June 2039, 21 years after the loan was granted?
- Calculate the interest Thabo will have paid over the first 21 years of the loan.
QUESTION 9
9.1 Determine f '(x) from first principles if it is given that f(x) = 2x2 – 3x. :
9.2 Determine
9.2.1 dy/dx if y=4x5 - 6x4 + 3x
9.2.2 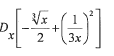
QUESTION 10
The graph of h(x) = ax3 + bx2 is drawn.
The graph has turning points at the origin, O(0; 0) and B(4:32).
A is an x-intercept of h.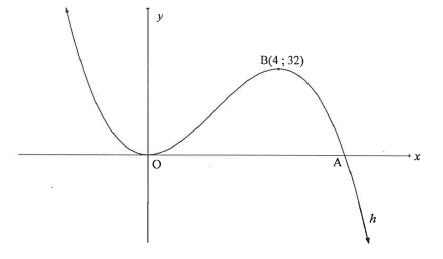
10.1 Show that a=-1 and b=6.
10.2 Calculate the coordinates of A.
10.3 Write down the values of x for which h is:
10.3.1 Increasing
10.3.2 Concave down
10.4 For which values of k will -(x-1)3 + 6(x-1)2 - k=0 have one negative and two distinct positive roots?
QUESTION 11
After travelling a distance of 20 km from home, a person suddenly remembers that he did not close a tap in his garden. He decides to turn around immediately and retum home to close the tap
The cost of the water, at the rate at which water is flowing out of the tap, is R1,60 per hour.
The cost of petrol is (1,2 + x/4000) rands per km, where x is the average speed in km/h.
Calculate the average speed at which the person must travel home to keep his cost as low as possible.
QUESTION 12
12.1 A and B are independent events. It is further given that: A and B are independent
P(A and B) -0,3 and Ponly B) -0,2
12.1.1 Are A and B mutually exclusive? Motivate your answer.
12.1.2 Determine:
- P (only A)
- P(not A or not B)
12.2 A teacher has 5 different poetry books, 4 different dramas and 3 different novels. She must arrange these 12 books from left to right on a shelf. 12.2.1 Write down the probability that a novel will be the first book placed on
the shelf.
12.2.2 Calculate the number of different ways these 12 books can be placed on the shelf if any book can be placed in any position.
12.2.3 Calculate the probability that a poetry book is placed in the first position, the three novels are placed next to each other and a drama is placed in the last position.
TOTAL: 150
INFORMATION SHEET
