MATHEMATICS INVESTIGATION GRADE 12 - 2022 ASSIGNMENTS
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS (INVESTIGATION: 2022)
GRADE 12
NATIONAL SENIOR CERTIFICATE
23 FEBRUARY 2022
INSTRUCTIONS
- The question paper consists of 5 questions.
- Answer ALL the questions on the spaces provided on the question paper.
- Clearly show ALL calculations.
- Write neatly and legibly.
QUESTION 1: TRANSPORT
Mr Dlamini transports people between Butterworth and East London using a bus which has a capacity of 100 people. The transport charge starts with a minimum charge of R8 and thereafter it was increased by R2 for each kilometre.
On a particular day the bus was full with passengers from Butterworth. In each and every kilometre there was a passenger getting off while no new passenger entered in the bus.
Mr Dlamini was calculating total money in his hand after each passenger was getting out.
The total amount he has after each stop can be written as a series as follows:
Sn = 8 + 10 + 12 + 14 +...
Use the series to calculate the following questions:
1.1
- Term 2 (T2) =……………..
Sum of first two terms (S2) =…………………(2) - Express T2 in terms of S1 and S2.
………………………………… (1)
1.2
- Term 3 (T3) =……………..
Sum of first three terms (S3) =…………………(2) - Express T3 in terms of S3 and S2.
………………………………… (1)
1.3
- Term 4 (T4) =……………..
Sum of first four terms (S4) =…………………(2) - Express T4 in terms of S3 and S4.
………………………………… (1)
1.4 Write the general formula to find the sum of the above series
………………………………………………… (2)
1.5 Did you observe any pattern from the answers in question 1.1, 1.2 and 1.3.
Explain your observation with respect to relation between term and sum of the terms.
……………………………………………………………………………………...
……………………………………………………………………………………… (2)
1.6 Use your deduction in activity question 1.5 to develop a formula between Tn, Sn and
Sn-1 where n > 1 and n ∈ ℕ.
………………………………………………………………………………………... (2)
1.7 Calculate T70 using formula identified in question 1.6.
………………………………………………………………………………………… (2)
[17]
QUESTION 2: MYSTIC ROSE
Following shape is called Mystic Rose.
This shape is formed by drawing chords between all points plotted on the circumference of
circle. The points in the circle in equal distance.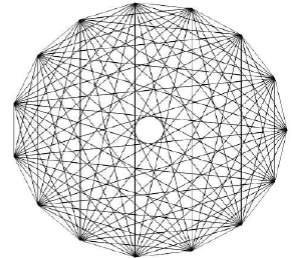
2.1 Consider the following circles:
- Draw a pattern of roses by means of chords connecting the points given in the circles provided.
- Connect each point to each other point on the circle by a chord and write the sequence you identified by counting the number of chords (3)
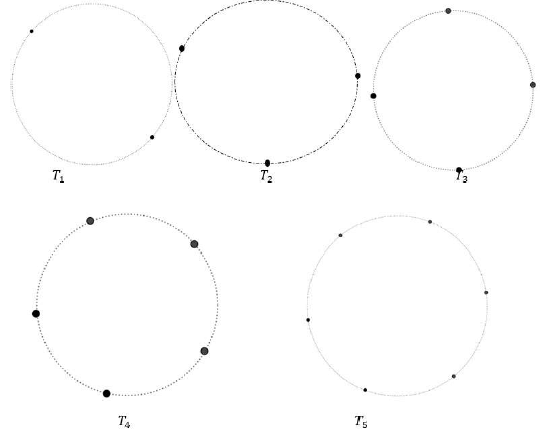
2.2 Write down the general formula for the nth term of sequence.
…………………………………………………………………………………………..
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………. (3)
2.3 Hence find the number of lines in the circle with 10 dots
…………………………………………………………………………………………..
………………………………………………………………………………………….. (2)
2.4 Calculate the value of T9 using the formula identified question 1.6
T9=………………………………………………………………………………………
………………………………………………………………………………….............. (3)
2.5 Describe your findings from activity question 2.3 and 2.4
…………………………………………………………………………………………..
………………………………………………………………………………………….. (1)
[12]
QUESTION 3: POCKET MONEY
Mr Reyan made an agreement with his son Smith who is studying in grade 12 as follows. Smith will get pocket money after he finishes all his homework every day. The amount of pocket money will be double the amount previous day. He will start first day with R1. He can use this saving for his matric dance.
3.1 Write the information as a sequence
…………………………………………………………………………………………. (1)
3.2 Write the formula for the nth term of above sequence
Tn = …………………………………………………………………………………….. (2)
3.3 Write the formula for the sum of n terms of the above series
Sn= ……………………………………………………………………………………... (2)
3.4 How much will Smith get on the 20th day if he successfully completed his homework.
…………………………………………………………………………………………..
…………………………………………………………………………………………. (2)
3.5 Calculate T20 using the formula identified in question 1.6
T20=……………………………………………………………………………………..
…………………………………………………………………………………………. (2)
3.5 Describe your findings from activity question 3.4 and 3.5
…………………………………………………………………………………………..
…………………………………………………………………………………………. (1)
[10]
QUESTION 4: EXPANSION QUESTION: Application
4. Given Sum of an arithmetic series is Sn = ?2 − 2? .
Determine the equation of Tn of this arithmetic sequence using the findings from previous
activities
Tn= ……………………………………………………………………………………………
……………………………………………………………………………………………….. (3)
[3]
QUESTION 5 : EXPANSION QUESTION : Sum Of Series
t is an even number in the series 1/t + 3/t + 5/t + ...t-1/t
5.1 Determine the number of terms in the series in terms of t.
…………………………………………………………………………………………..
…………………………………………………………………………………………..
…………………………………………………………………………………………..
………………………………………………………………………………………….. (2)
5.2 Determine the sum of the series in terms of t.
…………………………………………………………………………………………..
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………. (2)
5.3 Hence, or otherwise, evaluate:
(¼ + 3/4) + (1/6 + 3/6 + 5/6) + (1/8 + 3/8 + 5/8 + 7/8)+ ... +(1/50 + 3/50 + 5/50 + ... + 49/50 )
…………………………………………………………………………………………..
………………………………………………………………………………………….
………………………………………………………………………….........................
………………………………………………………………………………………….
…………………………………………………………………………………………
………………………………………………………………………………………… (4)
[8]
TOTAL: 50