TECHNICAL MATHEMATICS PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2019
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupTECHNICAL MATHEMATICS PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2019
INSTRUCTIONS AND INFORMATION
- Read the following instructions carefully before answering the questions.
- This question paper consists of NINE questions.
- Answer ALL the questions.
- Answer QUESTION 4.1.5 on the ANSWER SHEET provided. Write your centre number and examination number in the spaces provided on the ANSWER SHEET and hand in the ANSWER SHEET with your ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is attached at the back of the question paper.
QUESTION 1
The picture below shows the curved flight path of an aircraft. The flight path, as indicated by the arrows, is parabolic in shape and is defined by the equation:
P(x) = 2x2 - 8/81 
1.1.1 Factorise p(x) completely.
1.1.2 Hence, solve for x if p(x) = 0
1.2 Solve for x in EACH of the following:
1.2.1 (3x - 5)(x+2)=-13 where xe (Complex numbers)
1.2.2 (4 - x)(x+3) <0
1.3 Solve for x and y if:
y = 3x - 8 and x2 - xy + y2 = 39
1.4 The following formula represents the relationship between the voltage, the current and the impedance in an alternating current circuit: V = I x Z
Where:
V-Voltage (in volts)
I -Current (in amperes)
Z-Impedance (in ohms)
1.4.1 Express I as the subject of the formula.
1.4.2 Hence, determine in simplified form the value of I (in amperes) if:
V = 7i and Z=3-i
1.5 Simplify: 1012 x 112
QUESTION 2
2.1 Given: G = √p + 1
2p - 1
Determine the value(s) of p such that G will be as follows:
2.1.1 Undefined
2.1.2 Equal to zero
2.2 Determine for which value(s) of k the equation x2 - k + 4 = 5x will have real roots.
QUESTION 3
3.1 Simplify: (-2 4√a3)8
3.2 Solve for x: log,(3x - 2)+log2 0,5 = 3
3.3 If log 2-a and log 3.b, determine the value of log√0,6 in terms of a and b.
3.4 The voltage (V) in an alternating current circuit is represented by the Argand diagram below.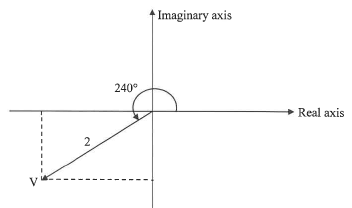
3.4.1 Use the Argand diagram above to write down the voltage in the form V=r(cosθ + i sinθ)
3.4.2 Hence, or otherwise, express V in rectangular form. Leave your answer in simplified surd form.
3.5 Determine the numerical values of m and n if m+ni =2(6-4i)-(-7i)
QUESTION 4
4.1 Given functions k and q defined by k(x) = (x - 5)(x + 3) and q(x)12/x -2 respectively.
4.1.1 Write down the x-intercepts of k.
4.1.2 Determine the x-intercept of q.
4.1.3 Determine the coordinates of the turning point of k.
4.1.4 Write down the equations of the asymptotes of q.
4.1.5 Sketch the graphs of k and q on the same set of axes provided on the ANSWER SHEET. Clearly show the asymptotes, the intercepts with the axes, as well as the coordinates of any turning points.
4.2 Sketched below are the graphs of p and h defined by p(x)=-√r2 - x2 and h(x) = ax + d respectively.
T is the point of intersection of p and h.
A(-1:- 2) is a point on h.
The asymptote of h is indicated by the dotted line.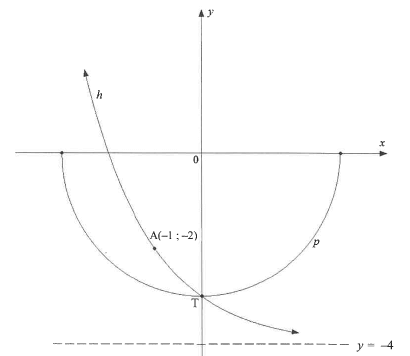
4.2.1 Write down the numerical value of d.
4.2.2 Show that h(x)= (½)x - 4
4.2.3 Hence, determine the coordinates of T.
4.2.4 Write down the range of p.
4.2.5 Hence, determine the defining equation w(x) of function w, such that w is the reflection of p in the x-axis.
4.2.6 Determine for which values of x will h(x) <p(x)
QUESTION 5
5.1 A small engineering business purchased a new welding machine. The value of the welding machine depreciated annually over a period of 5 years, as shown in the graph below.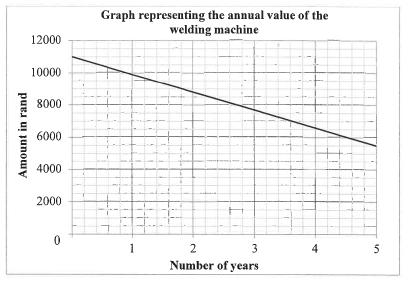
Use the graph above to answer the following questions:
5.1.1 Write down the value of the welding machine when it was new.
5.1.2 Calculate the annual constant percentage rate of depreciation.
5.2 A mechanic of Model X cars found a data sheet showing that 200 Model X cars had been serviced by the workshop during 2009. The annual compound growth rate of the number of Model X cars serviced by this workshop is 3,5% per annum.
Determine, showing ALL calculations, the year during which 273 Model X cars were serviced by this workshop. (5)
5.3 Anita planned to purchase a truck for her company in 8 years' time and decided to open an investment account to provide for the purchase of the truck. She deposited an initial amount of R293 000 into the account.
At the end of 2 years, Anita made a further deposit of R95 000 into the account. The interest rate for the first 4 years was 6,7% per annum, compounded quarterly, and for the remaining period the interest rate was 7,5% per annum, compounded monthly. The projected value of the truck at the end of 8 years will be R660 580.
Determine, showing ALL calculations, whether her investment would accumulate enough funds for her to purchase the truck at the end of the 8-year investment period. (8)
[17]
QUESTION 6
6.1 Determine f'(x) using FIRST PRINCIPLES if f(x) = 5 - ½x
6.2 Determine the following:
6.2.1 f'(x) if f(x)=a3 -0,5x3 - x-1
6.2.2 Dx[x(√x + 2)]
6.3 Given: xy + 2x3 = 7x6
6.3.1 Make y the subject of the equation.
6.3.2 Hence, determine dy/dx
6.4 A factory producing light bulbs makes a daily profit P(x) in rands for x number of light bulbs produced. The formula to calculate the factory's daily profit is given by P(x) = 0,8x2 - 200x, where x > 0.
Calculate:
6.4.1 The daily profit if 300 light bulbs are produced in one day
6.4.2 The number of light bulbs produced that will yield a zero daily profit
6.4.3 The rate of change of the daily profit with respect to the number of light bulbs produced, if 200 light bulbs are produced
[22]
QUESTION 7
The sketch below represents the graphs of functions g and f defined by g(x) - 9x + 18 and f(x)= x3 + bx2 + cx + d respectively.
S(3:0) and R are the turning points of f.
T is the y-intercept of both / and g.
Q is the x-intercept of both and g.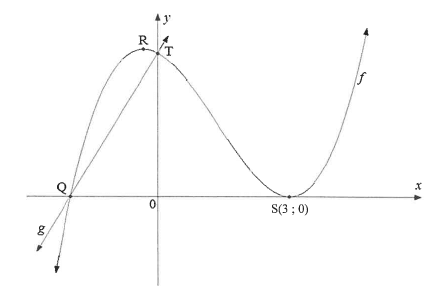
7.1 Determine the coordinates of Q and T.
7.2 Show that b=-4, C=-3 and d=18.
7.3 Hence, determine the coordinates of R.
7.4 Determine:
7.4.1 The equation of the tangent to the curve of functions at point R
7.4.2 The values of x for which g(x) > 0
7.4.3 The values of x for which f'(x)<0
QUESTION 8
A container consists of a right cylindrical part and a hemispherical part at the top, as shown in the picture and diagram below. The radius of both shapes is x cm and the total height of the container is (66-2x) cm.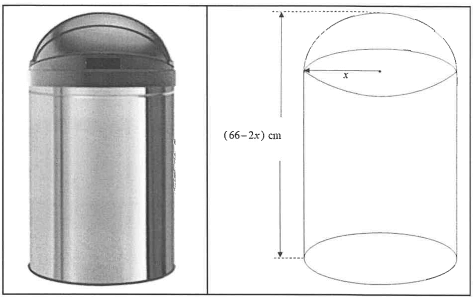
The following formulae may be used:
Volume of a right cylinder = πr2h
Volume of a sphere = 4/3 πr3
8.1 Write down, in terms of the height of the cylindrical part of the container.
8.2 Show that the formula for the total volume (in cm3) of the container is given by:
V = 66πx2 - 7/3 πx3
8.3 Hence, calculate the value of x that will maximise the total volume of the container,
8.4 Hence, determine the maximum total volume of the container.
QUESTION 9
9.1 Determine the following integrals:
9.1.1 ∫mxpdx where p≠ - 1
9.12 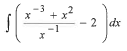
9.2 The sketch below shows the shaded bounded area of the curve of the function defined by g(x) =- 4/xwhere x>0.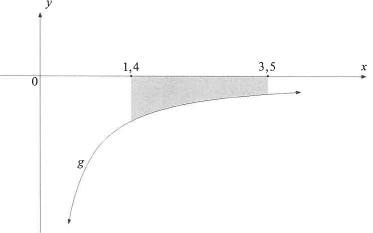
Determine (showing ALL calculations) the shaded area bounded by the curve and the x-axis between the points where x = 1,4 and x = 3,5.
TOTAL:150