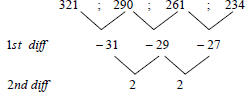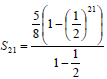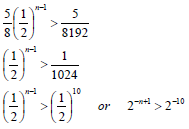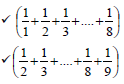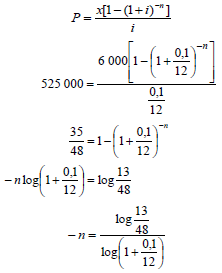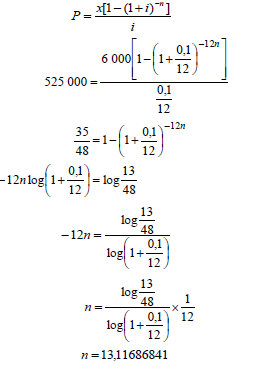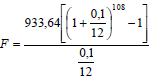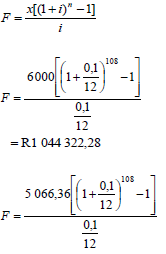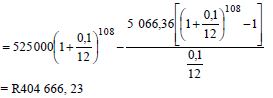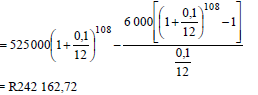MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2019
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
NOVEMBER 2019
MARKING GUIDELINES
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- Consistent Accuracy applies in all aspects of the marking memorandum.
QUESTION 1
1.1.1 | x2 + 5x - 6 = 0 | factors |
1.1.2 | 4x 2 + 3x - 5 = 0 |
substitution into the correct formula x = -1,55 |
1.1.3 | 4x 2 -1 < 0 | factors |
1.1.4 | (√√32 + x)( √√32 - x) = x | √32 - x2 |
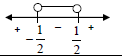
| 1.2 | y + x = 12 OR y + x = 12 | y subject of the formula substitution both values of x OR x subject of the formula |
| 1.3 | 3 6 9 12 15 18 21 24 27 30 3 3 32 3 3 32 3 3 33 3 k = 14 | identifying multiples of 3 |
| [22] |
QUESTION 2
2.1.1 | 209 ; 186 | 209 |
2.1.2 |
2a = 2 3a + b = -31 a + b + c = 321 | 2nd diff = 2 |
2.1.3 | n2 - 34n + 354 = 74 | equating Tn to 74 |
2.1.4 | f /(n) = 0 2n - 34 = 0 OR OR | 2n - 34 = 0 OR substitution OR substitution |
| 2.2.1 | a = 5/8 ; r = ½; n = 21 | r |
| 2.2.2 | Tn > 5 8 ; 16 ; 32 ; … ; 8192 | substitution into the correct formula calculating n answer (4) OR substitution into the correct formula method calculating n answer (4) |
| [19] |
QUESTION 3
3.1 |
|
|
3.2 | 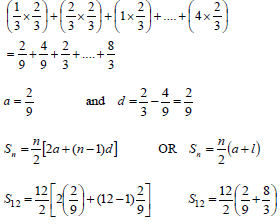 = 52 m2 = 52 m2 OR OR | a answer for both sides (6) OR a OR |
[9] |
QUESTION 4
4.1 | p = -1 | p = –1 (1) |
4.2 | y = a | coordinates D(0 ; –3) (3) |
4.3 | y = x 2 + 2x - 3 OR dy = 0 | substitution x = -1 substitution y = –4 OR derivative |
4.4 | y ∈ [-4;∞) or y ≥ -4 | - 4 |
4.5 | m = tan45° = 1 | gradient |
4.6 | No, the line passes through C and D OR | No OR |
| 4.7 | f (m - x) = f [-(x - m)] OR | value of m [19] |
QUESTION 5
5.1 | f (x) = k x | substitution (4 ; 16) | |||||
5.2 | f : y = 2 x | x = 2y | |||||
5.3 | 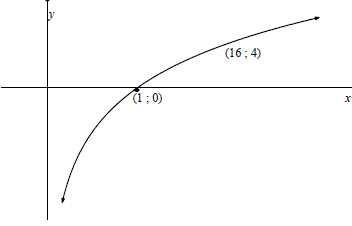 | asymptote | |||||
5.4.1 | x ∈ (1 ; ∞) or x > 1 | 1 | |||||
5.4.2 | 0 < x ≤ ½ or x ∈ [0; ½] | ½ | |||||
| 5.5 | 2x - 2-x = 15 22x -1 = 15 x 2x OR
| 2x - 2-x = 15 standard form OR 2x - 2-x = 15 answer | |||||
QUESTION 6
6.1 | Kuda : A = P(1+ in) = 5 000(1+ 0,083´ 4) = R6 660,00 Final Answer: R6 660,00 + R266,40 = R6 926,40 OR Kuda : A = P(1+ in) x 1,04 = 5 000(1+ 0,083´ 4) x 1,04 = R6 926,40 Thabo : A = P(1 + i)n = 5 000 (1 + 0.081 )12 x 4 Kuda will have a better investment | substitution into the correct formula OR substitution into the correct formula final answer substitution into the correct formula answer conclusion |
6.2.1 |
OR Number of payments = 13,11686841 x 12=157,40 | 0,1 substitution into the correct formula answer (5) OR substitution into the correct formula simplification 0,1 substitution into the correct formula
|
| 6.2.2 | Difference: R6 000 – R5 066,36 = R933,64 F = x[(1 + i)n - 1] OR OR Outstanding balance with monthly repayment of R5 066,35 | R933,64 OR n = 108 OR n = 108 |
QUESTION 7
7.1 | f (x) = 4 - 7x = lim 4 - 7(x + h) - (4 - 7x) = lim h(-7) = –7 | 4 - 7(x + h) substitution simplification answer |
7.2 | y = 4x8 + √x3 dy = 32x7 + 3 x½ | x3/2 32x7 3 x½ |
7.3.1 | y = ax2 + a | 2ax |
7.3.2 | y = ax2 + a | answer (2) |
| 7.4 | Substitute (2 ; b) in y = x + 12 Equation of perpendicular line: | value of b dy = 1 - 12 dx x2 gradient of perpendicular line equation (4) |
QUESTION 8
8.1 | 36cm | answer (1) |
8.2 | \t = 6 (-2t2 + 3t - 6) have no real roots | only once (3) |
8.3 | h(t) = -2t3 +15t 2 - 24t + 36 | expansion both values |
[8] |
QUESTION 9
9.1 | f /(x) = 9x2 | f /(x) = 9x2 |
9.2.1 | For f and f / | answer (1) |
9.2.2 | The point (0 ; 0) is : | f : inflection point |
9.3 | f // (x) = 18x | f // (x) = 18x |
9.4 | 3x3 - 9x2 < 0 | 3x3 - 9x2 < 0 x < 3 |
[13] |
QUESTION 10
10.1 | P(same day) = 4 or 1 | 4 numerator |
(2) | |
10.2 | P(2 consecutive days) = 3 x 2 = 3 | 3 x 2 | (3) | |
[5] | ||||
QUESTION 11
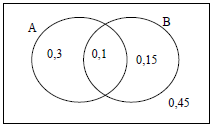
11.1.1 | P( A) x P(B) independent events | 0,1 0,15 and 0,3 0,45 (3) |
11.1.2 | P(A or not B) = P(A) + P(not B)- P(A and not B) OR P(A or not B) = 1 - P(only B) OR | substitution OR 1 – 0,15 OR |
11.2 | (5 × 1 × 5) + (5 × 1 × 6 )+ (5 × 1 × 6) + (5 × 1 × 5) =110 OR (5 × 2 × 5) + (5 × 2 × 6) = 110 OR 5 x 4 x 6 = 120 | 5 × 1 × 5 OR OR 5 x 4 x 6 = 120 |
| [11] |
TOTAL : 150