MATHEMATICAL LITERACY PAPER 1 GRADE 12 QUESTIONS - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
SEPTEMBER 2018
INSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions. Answer ALL the questions.
- 2.1 Use the addendum with ANNEXURE A for QUESTIONS 1.6.1 to 1.6.3.
2.2 Write your NAME and GRADE in the spaces provided on the ANSWER SHEET FOR QUESTION 4.6
Hand in the ANSWER SHEET with your ANSWER BOOK. - Number the answers correctly according to the numbering system used in this question paper.
- Diagrams are not necessarily drawn to scale, unless stated otherwise.
- Round off ALL final answers according to the context used, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Start EACH question on a NEW page.
- Show ALL calculations clearly.
- Write neatly and legibly.
QUESTION 1
1.1 The cost price of a shirt imported from China was R120 in June 2016 and R125 in June 2017.
1.1.1 Define the term inflation based on the above context. (2)
1.1.2 Write down the difference between the prices in cents (2)
1.1.3 Calculate the selling price of the shirt in 2017 with a 12,5% mark-up. (2)
1.2 John bought a pack of 60 eggs at a cost of R90. He sold half of the eggs at a price of R60 and the remaining eggs at a price of R75.
1.2.1 Calculate the cost of a dozen eggs. (2)
1.2.2 Calculate the total percentage profit made from the sale of 90 eggs. (3)
1.3 A bus left Pretoria for Queenstown on Thursday 4/01/2018 at 4:25 pm. It arrived in Queenstown on Friday 5/01/2018 at 3:30 am.
Calculate the total time taken for the journey from Pretoria to Queenstown. (3)
1.4 Determine the number of 275 mℓ plastic cups that can be filled with Coca-Cola from a 2 litre Coca-Cola bottle. (2)
1.5 A scale statement is shown as 100 cm : 75 m.
1.5.1 Calculate the actual length of a picture that has a length of 2 cm on the diagram. (3)
1.5.2 Write down the above scale as a unit ratio. (3)
1.6 The map in ANNEXURE A shows the school results per district in the Eastern Cape for the 2017 National Senior Certificate.
Use ANNEXURE A to answer the questions that follow.
1.6.1 Identify the best performing district. (2)
1.6.2 List the districts that performed poorer than Alfred Nzo East. (2)
1.6.3 Determine the district in the middle position from the seven best performing districts according to the results. (2)
1.6.4 The 2017 National Senior Certificate results for Mathematical Literacy showed that 73,9% out of 313 030 candidates passed. Determine the number of candidates that failed. (2)
[30]
QUESTION 2
2.1 TABLE 1 below shows an income and expenditure statement of John’s Vegetable Stall in a small town in the Eastern Cape.
The statement shows a comparison of budgeted and actual values for the year 2017.
TABLE 1
| John’s Vegetable Stall Budgeted and Actual values for the year 2017 (Values in Rand) | |||
| ITEM | INCOME | BUDGET | DIFFERENCE |
| Vegetables (Type S) sales | 3 250 | 2 750 | 500 |
| Vegetables (Type T) sales | 4 500 | 4 200 | 300 |
| Additional income from air time sales | 1200 | 1000 | 200 |
| Total Income | A | 7950 | 1000 |
| EXPENSES | BUDGET | VARIANCE | |
| Vegetables (Type S) costs | 1 440 | 1 500 | B |
| Vegetables (Type T) costs. | 2 600 | C | 200 |
| Airtime | 1 000 | 1 000 | 0 |
| Delivery | 800 | 880 | (80) |
| Total Expenses | 5 840 | 5 780 | 60 |
| Net profit (Loss) | 3 110 | 2 170 | 940 |
2.1.1 Calculate the value of A. (2)
2.1.2 Determine the value of B. (2)
2.1.3 Calculate the budgeted value C for the Vegetables type T. (2)
2.1.4 Identify the item within the ‘Expenses’ which could have been the main cause for the business to declare less profit. (2)
2.2 Mrs John, 68 years old, is a consultant at ABC company and earns a monthly gross salary of R65 000. She earns a performance bonus of 75 % of her monthly salary in December. Her pension contribution is 7,5% of her monthly gross salary and she pays R1 050 per month to the medical aid fund.
2.2.1 Calculate Mrs John’s annual gross salary. (2)
2.2.2 Calculate Mrs John’s annual pension fund contribution. (2)
2.2.3 Calculate Mrs John’s annual medical aid fund contribution. (2)
2.2.4 Show that Mrs John’s performance bonus is R48 750. (2)
2.2.5 Determine Mrs John’s annual taxable income. (4)
2.3 TABLE 2 below shows the income tax brackets for the 2016/2017 financial year.
| INCOME TAX FOR 2016/2017 FINANCIAL YEAR | |
| Taxable Income (Rand) | Rates of tax (Rand) |
| R0–R188 000 | 18% of each R1 |
| R188 001–R293 600 | R33 840 + 26% of the amount above R188 000 |
| R293 601–R406 400 | R61 296 + 31% of the amount above R293 600 |
| R406 401– R550 100 | R96 264 +36% of the amount above R406 400 |
| R550 101– R701 300 | R147 996+ 39% of the amount above R550 100 |
| R701 301 and above | R206 964 +41% of the amount above R701 300 |
| REBATES | TAX THRESHOLD |
| Primary: R13 500 | Below age 65: R75 000 |
| Secondary: R7 407 | Age 65 and over: R116 150 |
| Tertiary: R2 466 | Age 75 and over: R129 850 |
Use TABLE 2 and the information in QUESTION 2.2 to answer the questions that follow.
2.3.1 Identify the taxable income group in which Mrs John’s income falls. (2)
2.3.2 Calculate the rebate Mrs John will receive. (2)
2.3.3 Calculate the actual tax to the nearest rand that Mrs John will pay for the 2016/2017 financial year.
You may use the formula:
Actual tax = Income tax calculated on taxable income – Rebate (4)
2.3.4 Hence, calculate Mrs John’s net annual salary.
You may use the formula:
Net annual salary = Annual taxable income – Actual tax (3)
2.4 Mr Mana took out a loan of R400 000 from DFK Bank to fund his phone business. The loan was offered at an interest rate of 15,5% per annum compounded annually.
2.4.1 Calculate, without the use of a formula, the interest Mr Mana will have to pay for two years. (4)
2.4.2 Mr Mana specialises in two types of phones: Phone D and Phone E, that are imported from China at a cost price of R1 750 and R2 000 respectively. The prices include VAT of 15% (Value Added Tax).
Calculate the VAT amount on Phone D. (3)
2.4.3 He buys the phones in a ratio Phone D : Phone E = 3 : 2.
Determine the number of Phone E’s on an invoice with an order of 60 Phone D’s. (2)
2.4.4 Calculate the total cost of Phone D’s and Phone E’s he bought. (3)
2.4.5 Convert the total cost of the phones in Chinese Yuan.
Use the exchange rate: R1 = 0,52709 Chinese Yuan (CNY) (3)
[46]
QUESTION 3
3.1 The diagram below shows the minimum opening sizes of a double door garage, surrounded by a wall built of a single layer of bricks.
Study the diagram and answer the questions that follow.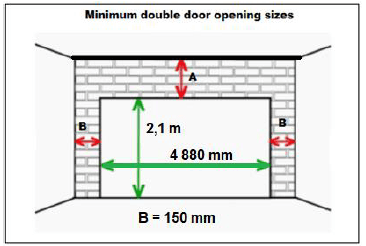
3.1.1 Identify the length of the minimum double door opening. Give your answer in metres. (2)
3.1.2 A is triple the distance marked B. Write down the distance marked A. (2)
3.1.3 Write down the height of the wall in metres. (3)
3.1.4 Determine the area of the single garage door opening if length is half the length of the double door garage opening and the height remains the same.
You may use the formula: ????=?????? ? ????? (4)
3.1.5 Calculate the area covered by bricks in m2.
You may use the formula: ????=?????? ? ????? (5)
3.2 Asange plans to increase the height of the wall behind her house by 2,5 m because of burglaries.
The standard size of the brick to be used is 230 mm by 110 mm by 76 mm.
3.2.1 Calculate the height of the brick and cement, if cement of 12 mm thickness is used around the bricks when laying them. (2)
3.2.2 Determine the number of rows (layers) of bricks needed to increase the height of the wall, if the bricks are lengthwise along the wall. (3)
3.2.3 Calculate the volume of the standard size brick in cm3.
You may use the formula:
Volume =?????? × ?????×?????? (4)
[25]
QUESTION 4
Needo Angling Club had two club competitions, an overnight at Bridal Drift Dam in August and a day competition at Nahoon Dam in September 2017.
| AUGUST COMPETITION BRIDAL DRIFT DAM | Hours worked for both competitions | SEPTEMBER COMPETITION NAHOON DAM | ||
| Weight (kg) | Number of fish | Weight (kg) | Number of fish | |
| 1,26 | 2 | 1st | 0,182 | 3 |
| 1,371 | 9 | 2nd | 0,309 | 1 |
| 1,668 | 8 | 3rd | 0,729 | 3 |
| 1,746 | 4 | 4th | 0,856 | 4 |
| 1,849 | 8 | 5th | 0,936 | 1 |
| 2,163 | 1 | 6th | 2,448 | 2 |
| 2,333 | 1 | 7th | 2,449 | 1 |
| 3,128 | 2 | 8th | 3,038 | 1 |
| 9th | 3,316 | 6 | ||
4.1 Determine the range for the weights in the September competition. (3)
4.2 Write down the median weight for the August competition. (2)
4.3 Calculate the average weight for all the fish caught during the August competition. Give your answer to the nearest kilogram. (3)
4.4 Calculate the total number of fish that were caught during the day competition. (2)
4.5 Express as a percentage the probability of randomly selecting a fish that weighs 1,849 kg from the August competition. (3)
4.6 Use the information from the August competition to draw a bar graph on the ANSWER SHEET. (6)
4.7 Determine the third (upper) quartile for the September competition. (3)
4.8 Determine the modal weight for the September competition. (2)
4.9 Express the number of fish with a weight of 1,668 kg as a percentage of the total fish caught during the competitions. (3)
4.10 Identify the hour at which the most number of fish was caught. (2)
4.11 Arrange the number of fish caught during the September competition, in ascending order. (2)
[31]
QUESTION 5
Study the cinema seating plan below and answer the questions that follow.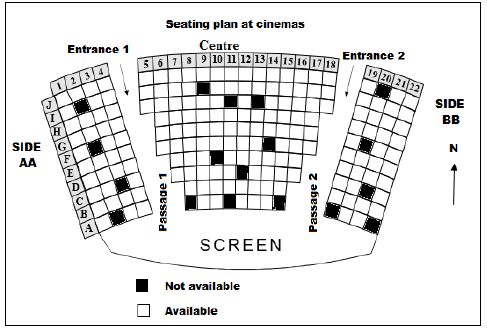
5.1 Lundi holds a ticket numbered K4 and enters the cinema using entrance 2. Assist Lundi to find his seat. (2)
5.2 In which general direction does seat J5 face? (2)
5.3 Allocate seat numbers for the seats that are not available on the front row at the centre of the cinema. (3)
5.4 Write down the total number of available seats on the north-eastern side of the screen. (2)
5.5 Asi gets into the cinema through entrance 1. She goes down the passage, enters the second front row on her left and takes the second last seat.
Write down Asi’s seat number. (2)
5.6 Identify the row furthest from the screen. (2)
5.7 Write down the side with the least number of available seats. (2)
5.8 Write down the probability of randomly selecting a seat with letter G from the total seats. Give your answer as a decimal fraction. (3)
[18]
TOTAL: 150
GRAPH FOR QUESTION 4.6