TECHNICAL MATHEMATICS PAPER 2 GRADE 12 MEMORANDUM - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS

More in this category: « ACCOUNTING GRADE 12 QUESTIONS - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS TECHNICAL MATHEMATICS PAPER 2 GRADE 12 ERRATA - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS »
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

TECHNICAL MATHEMATICS PAPER 2
GRADE 12
NATIONAL SENIOR CERTIFICATE 
MEMORANDUM
SEPTEMBER 2018

NOTE:

  • Continuous accuracy (CA) applies in ALL aspects of the marking guideline.
  • After two mistakes, do not apply CA marking.
  • Assuming values/answers in order to solve a problem is unacceptable.
Symbol Explanation
M Method
MA Method with accuracy
A Accuracy
CA Consistent accuracy
S Simplification or Statement
R Reason

 

QUESTION 1  
1  
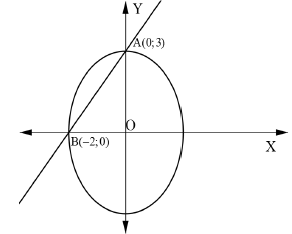1.1 AB = √( x2 - x1 )2  + ( y2  - y1)2
= √(0 + 2)2  + (3 - 0)2
= √4 + 9
≈ 3, 61		 ✓MA formula & substitution
✓S Simplification
✓CA Answer in decimal format		 (3)
  OR    
AB2 = OB2 + OA2 (Pyth)
=22 + 32
= 4 + 9
AB =√13
≈ 3, 61
 ✓MA Pythagoras
✓S Simplification
✓CA Answer in decimal format		 (3)
1.2 mAB = y2 - y1
            x2 - x1
= 3 - 0
   0 + 2
= 3/2
Equation of the line:
y - y1 = m ( x - x1 )
y - 0 = 3/2 ( x + 2)
y = 3/2 x + 3		 ✓MA formula & substitution
✓M Formula equation of line
✓A Substitute pt A or B
✓CA Answer in standard form		 (4)
1.3 tanOBA = mBA
tan OBA = 3/2
OBA = 56, 31°
OAB= 90°- 56, 31°= 33, 69°		 ✓A subst. into correct formula
✓CA value of OBA 
✓CA value of OAB		 (3)
1.4 Scalene triangle OR Right angled triangle ✓A (1)
1.5 a = 2
b = 3
Equation of ellipse
x 2 + y 2 =1
4      9		 ✓A value of
✓A value of
✓CA Equation of ellipse		 (3)
      [14]

 

QUESTION 2
2
2.1

r 2 = x2 + y2
= (-8)2  + 62
= 64 + 36
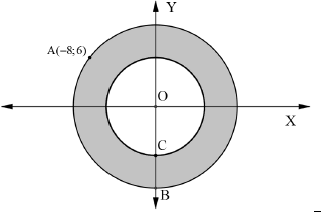= 100
r = 10
B(0 ; – 10)

 ✓M Calculating
✓CA Value of r
✓A x = 0
✓CA y = – 10 (neg. value)
(4)
2.2 Radius of smaller circle
= 10 – 4 = 6
equation of smaller circle
x2 + y2 = 36		 ✓M radius of smaller circle
✓CA Equation of smaller circle
(2)
2.3 Bigger circle
mradius= y2 - y1           
              x2 - x1 
= 6 - 0
  -8 - 0
=- 3/4
mtangent = 4/3
equation of tangfent:
y - y1 = m ( x - x1 )
y - 6 = 4/3( x + 8)
y = 4/3 x + 32/3 + 6        3=4/3 x + 50/3		 ✓MA gradient of radius of bigger circle
✓CA Gradient of tangent
✓A Subst. A into equation
✓CA Standard form of equation
(4)
    [10]

  

QUESTION 3  
3  
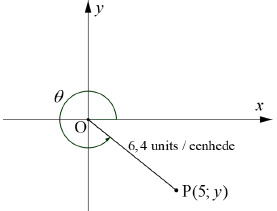3.1 3.1.1 x2 + y2 = r 2(Pyth)
52 + y2 = 6, 42
y = - √40, 96 - 25
=-√15, 96
= -3, 99...
≈-4 units
 ✓A Pythagoras
✓A Substitution
✓CA Simplification
✓CA Rounded answer		 (4)
  3.1.2 cotθ- cos ecθ x sin2 θ
= 5/-4 - 6,4/-4 x (-4/6,4) 2
= -5/4 + 6,4/4 x 16/40,96
= 5		 ✓CA cot θ
✓CA cosec θ
✓CA Sin θ
✓CA Simplification of sin2 θ
✓CA Answer		 (5)
  3.1.3 cosθ = 5/6.4
θ = 360° - cos-1 (5/6.4)
= 360° - 38, 624...°
= 321, 4°		 ✓A Ratio
✓CA Reference ∠
✓A 4th Quadrant
✓CA Answer, rounded		 (4)
3.2 sin (180° + x) tan (360° + x)cos(180° - x)
= (-sin x)(tan x)(-cos x)
= (-sin x) sin x (-cos x)
              cos x
= sin2 x		 ✓A sin x
✓A tan x
✓A -cos x
✓A sin x
     tan x
✓CA answer
 (5)
3.3 tan 2 5x ✓A tan 2 5x (1)
3.4 2 tan ( x - 23°) + 5 = 0
tan ( x - 23°) = -5/2
Ref ∠ = tan-1 (2,5) = 68,19...°
x - 23° = 180° - 68,19...° OR 360°- 68,19...°
x = 111,8...° + 23° OR 291,80...° + 23°
= 134,8° or 314,8°		 ✓A RHS = -2,5 
✓CA Ref ∠
✓CA 2nd quadrant
✓CA 3rd quadrant
✓A Adding 23° by
✓CA Answers		 (6)
      [25]

 

QUESTION 4 
4
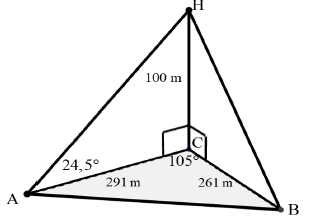4.1 In ∆AHC:
AH =cosec24,5°
HC
AH= 100 
     sin24,5°
≈241 m		 ✓A Ratio
✓A Substitution
✓CA Rounded answer		 (3)
4.2

In ∆BHC:
tan B = HC
            BC
= 100
   261
= 0, 383141...
B = tan-1(0, 383141...)
≈ 21°

 ✓A Ratio
✓A Substitution
✓CA Rounded answer

 (3)
4.3 AB2 = AC 2 + BC 2 - 2AC x BC cos ACB
= 2192 + 2612 - 2´ 219´ 261´cos105°
= 145669, 6756
AB = 381, 6669...
≈ 382 m

✓A cos rule
✓CA substitution
✓CA simplification
✓CA answer

 (4)
4.4 Area DABC = 1 ab sin C2
= 1 ´ 261´ 219 ´sin105° 2
= 3000847, 5
» 3 000 848 m2		 ✓A Area rule
✓CA Substitution
✓CA value of Area		 (3)
      [13]

QUESTION 5 
 5
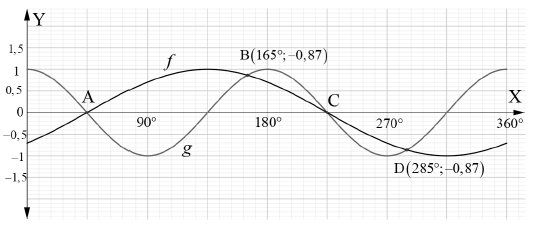5.1 Period = 360° = 180°
                2		 ✓A Answer (1)
5.2 A(45°; 0) & C(225°; 0) ✓A A(45°; 0)
✓A C(225°; 0)		 (2)
5.3 90° < x < 180°

✓A End points
✓A Notation

 (2)
5.4 45° < x < 165° and/en 225° < x < 285° ✓A✓ A first
✓A✓ A second		 (4)
5.5 y ∈ [-3;3] or - 3 ≤ y ≤  3 ✓A critical values
✓A notation		  (2)
      [11]

 

QUESTION 6  
6.1 SupplementaryOR Add up to 180° completed (1)
6.2 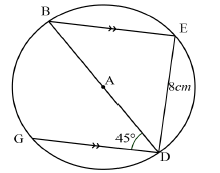6
  6.2.1 E = 90°   (∠ in semi-circle) ✓S ✓R (2)
  6.2.2 BDE = 45°   (co-int∠s ;BE//GD) ✓S ✓R (2)
  6.2.3 BE = ED = 8 cm (sides opp. = angles) ✓S ✓R (2)
  6.2.4 BGD = 90°   (∠ in semi-circle)
BGDE is a rectangle (All Ðs = 90°)
BGDE is a square (diagonals bisect at 45°)
GD = 8 cm (all sides=)		 ✓SR
✓SR
✓SR
✓S		 (4)
6.3 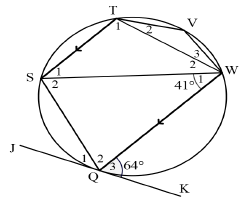7
  6.3.1 S1 = 41° (alt ∠s ; TS // WQ) ✓S ✓R (2)
  6.3.2 V = 139° (opp ∠s of cyclic quad) ✓S ✓R (2)
  6.3.3 S2 = 64°      (tan-chord) ✓S ✓R (2)
        [17]

 

QUESTION 7
7.1 Divides the other two sides proportionally ✓ completed statement   (1)
8
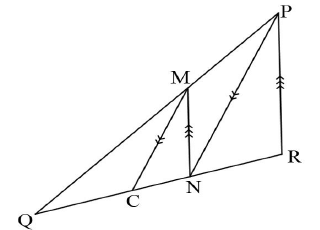7.2 7.2.1 Let QC = x.
QC = QM  (prop th; MC // PN)
CN     MP   
  x   = 3 
2,86   2
x = 3 x 2,86
          2
= 4, 3 cm		 ✓ S
✓R Proportionality
✓S Set up proportion
✓S Simplification
✓S Answer		 (5)
  7.2.2 Let NR = y.
QN = QM (prop th/ewer. st; MN // PR)
NR    MP
7,15 = 3 
  y       2
y = 2 x 7,15
            3
= 4,8 cm		 ✓R Proportionality MN // PR
✓S Set up proportion
✓S Simplification
✓S Answer		 (4)
7.3  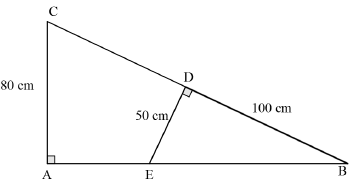9
  7.3.1  Bˆ  is common
BDE = 90° = A
DBDE /// DBAC (AAA)		 ✓S
✓S
✓R		 (3)
  7.3.2  BE =    502 +1002    (Pyth)
≈112 cm
Let AE = x cm
BD = DE    (/// Δs)
BA    AC
  100    = 50 
x +112     80
x +112 = 80 x100
                   50
x = 48 cm		 ✓S BE = 112
✓S Proportionality
✓S setup proportion
✓S value of AE

 (4)
  7.3.3 

Area DBDE = ½ x DE x DB
Area DBAC    ½ x AC x AB
= 50´10080´160
= 0, 39

 ✓S formulae
✓S substitution
✓S value of ratio		 (3)
  7.3.4  Area AEDC = Area ABC – Area DBE
= 6400 – 2500
= 3900 cm2		 ✓MA
✓CA value of area 		 (2)
        [22]

 

QUESTION 8  
8.1 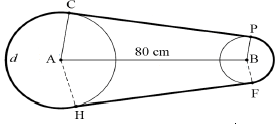10  
  8.1.1 reflex CAE = 2/3 x 360°
= 240°		 ✓A Multiply by
2/3 x 360°		 (1)
  8.1.2 obtuse CAE = 360° - 240°
= 120°CAB
= 60°		 ✓S
✓S		 (2)
  8.1.3 d = s = rθ
= 50 x 240° x  π  
                     180
= 200π
      3
≈ 209 cm		 ✓A Formula
✓A Multiply 180°
✓A Substitution
✓CA Answer
✓CA Rounding		 (5) 
  8.1.4 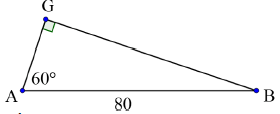11
ACP = 90° (tan ⊥ radius)
G = 90°(corrsp ∠s; BG || CP)
GB = sin 60°
80
GB = √3 x 80
          2
= 40√3
≈69 cm
CP = GB = 69 cm		 ✓A G  = 90°  Ratio
✓A Ratio
✓CA Simplification
✓CA Answer
✓A CP = GB		 (5)
    OR 
GA = AC – BP (opp sides of rectangle)
= 50 – 10 = 40 cm
GB » 69 cm (Pyth)
CP = GB = 69 cm		 OR
✓A G = 90°  Ratio
✓A GA = 40 cm
✓CA Pythagoras
✓CA Answer
✓A CP = GB
 (5)
  8.1.5 Length of belt
= CH + HF + FP + CP
= 209 +69 + 21 + 69
= 368 cm		 ✓A HF = CP
✓CA Answer		 (2)
8.2 d = 19
x = 13
4h2 - 4dh + x2= 0
4h2 - 4 (19) h +132 = 0
4h2 - 76h +169 = 0
h = -b ± √b2 - 4ac
               2a
= 76 ± √(-76)2 - 4 (4)(169)
                    2(4)
= 76 ± √3072
         8
3 cm and 16 cm		 ✓A Formula
✓A Substitusie
✓M Standard form
✓A Quadratic formula
✓CA Subsitutisie
✓CA Answers
✓A Rounding		 (7)
        [22]

 

QUESTION 9

9.1

9.1.1

w = 2πn
= 2π(35)
= 70p » 219, 9 rad/s

✓A Formula
✓A Substitution
✓CA Answer / antwoord

(3)
 

9.1.2

D = 40 cm = 0, 4 m
v = πDn
= π(0, 4)(35)
= 14π
= 43, 98 m/s

✓A Convert to m
✓A Formula
✓CA Substitution
✓CA Answer

 (4)

9.2

Vrectangluar = l x b x h
= 5 x 7 x 12
= 420 cm3
Vcylinder = πr 2h
420 = πr 2 (60)
r 2 = 420  = 2,228...
        60π
r = 1,492...
diameter = 2r
≈ 2,99 cm

✓A Subst. into formula 
✓CA Answer
✓A Formula
✓CA Substitution
✓ CA Value of diameter

 (5)
       

[12]

 

QUESTION 10 
Ar = a(o1 + on + o2 + o3 + o4 + ... + on-1)
               2
= 5(8 + 3 + 10 + 9 + 9 +4)
         2
= 187.5cm2 OR
AT = a(m1 + m2 + m3 + ... + mn)
= 5(8 + 10 + 10 + 9 + 9 + 9 + 9 + 4 + 4 + 3)
           2           2            2          2          2
= 187.5cm2		 ?formula
?value of a
?substitution
?Area
OR
?formula
?value of a
?substitution
?Area		 (4)
TOTAL   150
Last modified on Wednesday, 08 September 2021 09:42
Published in Grade 12 September 2018 Preparatory Examinations

Related items

More in this category: « ACCOUNTING GRADE 12 QUESTIONS - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS TECHNICAL MATHEMATICS PAPER 2 GRADE 12 ERRATA - 2018 SEPTEMBER PREPARATORY EXAM PAPERS AND MEMOS »
back to top