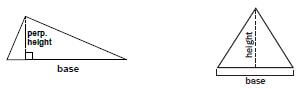MEASUREMENT GRADE 12 NOTES - MATHEMATICAL LITERACY STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Converting between different units of measurement
- Metric conversions
- Activity 1: Converting units
- Cooking conversions and temperature
- Measuring length
- Activity 2: Measuring length
- Measuring mass or weight
- Activity 3: Measuring weight
- Activity 4: Cost and weight
- Measuring volume and capacity
- Activity 5: Measuring volume
- Activity 6: Cost and volume
- Perimeter, area and volume
- Estimation and direct measurement of perimeter
- Activity 7: Measuring perimeter
- Activity 8: Combining shapes
- Using formulae to calculate area
- Activity 9: Combining areas
- Using formulae to calculate volume
- Activity 10: Calculating volume
- Activity 11: Multi-step volume problem
- Calculating elapsed time
- Activity 12: Calculating elapsed time
- Calendars
- Timetables
- Activity 13: Drawing up a timetable
- Activity 14: Reading a time table
Measurement
In this chapter learners need to apply some of the skills from Chapter 3, such as changing the subject of a formula and correctly substituting values into a formula. Remember that the units are important when you work with measurements.
4.1 Converting between different units of measurement
You need to memorise the conversions between metric units.
Length
Conversion factors for length |
10 millimetres (mm) = 1 centimetre (cm) |
1 000 millimetres (mm) = 1 metre (m) |
100 centimetres (cm) = 1 metre (m) |
1 000 metres (m) = 1 kilometre (km) |
Note:
- To convert to a smaller unit, we multiply. To convert to a larger unit, we divide.
Here is a visual representation of converting between units of length: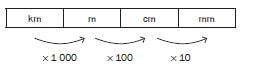
We can also reverse it to find lengths in larger units: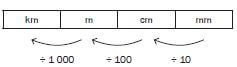
Volume
Conversion factors for volume |
1 000 millilitres (mℓ) = 1 litre (ℓ) |
1 000 litres (ℓ) = 1 kilolitre (kℓ) |
Here is a visual representation of converting between units of volume: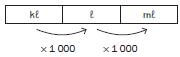
And you can also reverse it: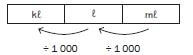
Weight
Conversion factors for weight |
1 000 mg (mg) = 1 gram (g) |
1 000 grams (g) = 1 kilogram (kg) |
1 000 kilograms (kg) = 1 tonne (t) |
Here is a visual representation of converting between units of weight: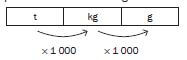
And one can also reverse it: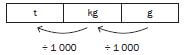
e.g. Worked example 1
Convert the following units. Remember to show all of your calculations.
- A leaf is 25 mm long. How long is it in cm?
- A sofa is 187 cm How long is it in metres?
- Harry’s household uses 1 023 ℓ of water per How much water do they use in kℓ?
- A tin contains 3,5 ℓ of How many millilitres of paint is in the tin?
- The cover of a book is 16,2 cm long. How long is the book in mm?
- A medicine tablet weighs 50 How much does the tablet weigh in grams?
- A shopping bag weighs 2 850 How heavy is the bag in kg?
Solutions
- Converting to a larger unit, divide by 10: 25 mm = 2,5
- Converting to a larger unit, divide by 100: 187 cm = 1,87
- Converting to a larger unit, divide by 1 000: 1 023 ℓ ÷ 1 000 = 1,023 kℓ.
- Converting to a smaller unit, multiply by 1 000: 3,5 × 1 000 = 3 500 mℓ.
- Converting to a smaller unit, multiply by 10: 16,2 cm × 10 = 162
- Converting to a larger unit, divide by 1 000: 50 mg ÷ 1 000 = 0,05
- Converting to a larger unit, divide by 1 000: 2 850 ÷ 1 000 = 2,85
Do the conversions.
- A tennis court is 23,78 m long. Convert to cm. (1)
- Thabiso fills a bath with 23,7 ℓ of water. How much water is this in mℓ? (1)
- The distance between Cape Town and Betty’s Bay is 90,25 km.How far is this in metres? (1)
- The distance from Phumza’s house to the shop is 1 890 000 mm.How far is this in kilometres? (1)
- A can of cola has a capacity of 330 mℓ. How many litres of cola is this? (1)
- A boulder weighs 2,35 t. Convert the weight of the boulder into grams. (1)
- A book weighs 0,85 kg. Convert the weight of the book into grams. (1)
- Jack and Thembile live 6 473 m apart. Convert this distance to km. (1)
- The dam on Cara’s farm contains 6,025 kℓ of water. How much is this in litres? (1)
- A playground is 4,02 m wide. How wide is the playground in cm? (1)
- A car weighs 1 250 000 g. What is the mass in tonnes? (1)
- A long workbench is 295 cm long. How long is it in metres? (1) [12]
Solutions | ||
1. A tennis court is 23,78 m long. | 23,78 × 100 = 2 378 cm ✓ | (1) |
2. Thabiso fills a bath with 23,7 ℓ of water. | 23,7 × 1 000 = 23 700 mℓ ✓ | (1) |
3. The distance between Cape Town and Betty’s Bay is 90,25 km. | 90,25 × 1 000 = 90 250 m ✓ | (1) |
4. The distance from Phumza’s house to the shop is 1 890 000 mm. | 1 890 000 ÷ 1 000 000 = 1,89 km ✓ | (1) |
5. A can of cola has a capacity of 330 mℓ. | 330 mℓ ÷ 1 000 = 0,33 ℓ ✓ | (1) |
6. A boulder weighs 2,35 t. | 2,35 t × 1 000 000 = 2 350 000 g ✓ | (1) |
7. A book weighs 0,85 kg. | 0,85 × 1 000 = 850 g ✓ | (1) |
8. Jack and Thembile live 6 473 m apart. | 6 473 ÷ 1 000 = 6,473 km ✓ | (1) |
9. The dam on Cara’s farm contains 6,025 kℓ of water. | 6,025 × 1 000 = 6 025 ℓ ✓ | (1) |
10. A playground is 4,02 m wide. | 4,02 × 100 = 402 cm ✓ | (1) |
11. A car weighs 1 250 000 g. | 1 250 000 ÷ 1 000 000 = 1,25 t ✓ | (1) |
12. A long workbench is 295 cm long. | 295 ÷ 100 = 2,95 m ✓ | (1) |
[12] | ||
4.1.2 Cooking conversions and temperature
In recipes used for cooking and baking we often find the measurements for the ingredients required in cups, teaspoons and tablespoons. Measuring cups and spoons come in standard sizes, and are common in the kitchen and in recipes because they are quick and simple to use.
If you don’t have measuring spoons and cups, you can use everyday household objects to approximate the same quantity of ingredients. For example, a small tea cup is roughly the same size as a measuring cup and a heaped, normal-sized spoon is about the same quantity as a measuring tablespoon. When following a recipe though, it is important to be as accurate as possible with your measurements, so using these rough approximations is often not suitable.
The following table shows some of the conversions used in cooking:
Conversions for cooking and baking |
1 cup = 250 mℓ |
1 tablespoon (tbsp) = 15 mℓ |
1 teaspoon (tsp) = 5 mℓ |
Note: you will be given these conversions in assessments
Estimation is used to find approximate values for measurements. For example, one metre is approximately the length from your shoulder to your fingertips, if you stand with your arm outstretched. A metre is also approximately the distance of one large step or jump.
e.g. Worked example 2
Carl needs to measure the width of a window, to find out how much material he must buy to make a curtain. The curtain material costs R55 per metre on sale, sold only in full metres.
- Carl estimates the width of the window to be 1,9 metres wide (using his arm). If Carl goes to the shop with this estimate:
- How many metres of material should he buy?
- How much would the material cost?
- Carl decides to double-check his estimated measurement before he buys the material and so he uses his tape measure to accurately measure the width of the He determines that the window is actually 2,2 m wide.
- How many metres of material does he need to buy?
- How much will the material cost?
Solutions
- (i) 2 m
(ii) 2 × R55 = R110 - (i) 3 m (as the material is only available in units of 1 metre)
(ii) 3 × R55 = R165
e.g. Worked example 3
Liz sews dresses for children. The material costs R89,50 per metre and she needs 2 metres of material to make a dress for a 4 year old; 2,5 metres to make a dress for a 7 year old and 3 metres to make a dress for 10 year old. The embroidery cotton costs R12,55 for a roll of 3 metres. She uses 2 rolls of cotton per dress.
- How many metres of material will she need to make the following four dresses:
1 dress for a 7 year old, 2 dresses for four year olds, and 1 dress for a 10 year old? - What will the material cost for the four dresses?
- What is the length of embroidery cotton that Liz is going to use when sewing one dress, in metres and centimetres?
- What is the total amount that she will pay for the embroidery cotton?
- What is the total cost of a dress for a 10 year old?
Solutions
- 2,5 m + 2 m + 2 m + 3 m = 9,5 m
- Length of material × price
= 9,5 m × R89,50
= R850,25 - Length of one roll of cotton × 2 = 3 m × 2
= 6 m, or 600 cm per dress - Number of dresses × 2 rolls of cotton per dress × price
= 4 × 2 × R12,55
= R100,40 - (Length of material × price) + (2 rolls of cotton × price)
= (3 m × R89,50) + (2 × R12,55)
= R268,50 + R25,10
= R293,60
Jenny has started a decorating business and has a contract to provide decor at a wedding reception.
- The tables used at this wedding are rectangular with a length of 3 m and a width of 1 m as shown The fabric she plans to use for the tablecloth costs R75 per metre (but can be bought in lengths smaller than a metre) and is sold in rolls that are 1,4 m wide. The bride and groom want the tablecloths to hang at least 20 cm over the edges of the tables. Calculate the cost of the cloth for each table. (2)
- If there are 15 tables at the wedding, calculate how much she is going to spend on tablecloths (1) [3]

Solutions
- 3,4 × 1,4 × 75 = (3,4 × 75) ✓ in 1,4 m width = R255,00 ✓
- R3 825,00 ✓
- The scientific word for how much an object weighs on a scale is “mass”.
- In this book we will use the words “weight” and “mass” interchangeably, because both are used in everyday language.
Worked example 4
- A lift in a shopping mall has a notice that indicates that it can carry 2,2 tonnes or a maximum of 20 Convert the tonnes measurement to kilograms and work out what the engineer who built the lift estimated the average weight of a person to be.
- A long distance bus seats 50 passengers and allows each passenger to each have luggage of up to 30
- If 50 people, with average weight of 80 kg per person, each have one piece of luggage that weighs an average of 29 kg, what would be the total load carried by the bus, in tonnes?
- If the bus weighs 4 tonnes, how much does it weigh in total (in kg) including all the passengers and the luggage?
- Sweet Jam can be bought in bulk from a warehouse in boxes that contain 25 tins of 250 g
- Calculate the total weight of the jam in each box, in
- If a trader orders 15 boxes of Sweet Jam, calculate the total weight of his order in
Solutions
- 2,2 t = 2 200 kg. 2 200 kg ÷ 20 people = 110 kg each
- (i) (50 × 80 kg) + (50 × 29 kg)
= 4 000 kg + 1 450 kg
= 5 450 kg
= 5,45 t
(ii) 4 t = 4 000 kg. 4 000 kg + 5 450 kg = 9 450 kg - (i) 250 g × 25
= 6 250 g
= 6,25 kg
(ii)15 boxes × 6,25 kg = 93,75 kg
You should never carry more than 15% of your body weight. Elias weighs 66 kg and his backpack, with school books, weighs 12 kg. Elizabeth weighs 72 kg and her school bag, with school books, weighs 8 kg.
- Determine 15% of Elias’s Is his bag too heavy for him? (1)
- Determine 15% of Elizabeth’s Is her bag too heavy for her? (1)
Solution
- 9,9 The bag is too heavy for him because it weighs more than 9,9 kg. ✓ (1)
- 10,8 kg. The bag is not too heavy for her because it weighs less than 15% of her body ✓ (1) [2]
e.g. Worked example 5
Khuthele School has two soccer fields. The grass needs to be covered with fertiliser. A 30 kg bag of fertiliser costs R42,60. The school needs to buy 96 bags.
- How much will they pay for the fertiliser?
- How many kg of fertilizer will they buy in total?
Solutions
- Number of bags × price
= 96 × R42,60
= R4 089,60 - Number of bags × weight of one bag
= 96 × 30 kg
= 2 880 kg
e.g. Worked example 6
Mr Booysens needs to buy sand to build a new room onto his house. Sand is sold for R23 per kg. Mr Booysens needs to buy 0,8 tonnes of sand in order to build the room.
- Write the amount of sand needed in
- Calculate the total amount of money he will have to spend to buy enough sand for the
- If sand is only sold in 50 kg bags, how many bags will Mr Booysens need to buy?
Solution
- Remember that 1 tonne = 1 000 kg
so he needs 0,8 tonnes × 1 000 kg = 800 kg - Quantity of sand needed × Cost per kg
= 800 × 23
= R18 400 - He will need: 800 kg ÷ 50 kg
= 16 bags of sand
A chef is preparing a meal that needs 3,75 kg of rice and 1,5 kg of beef. The recipe will feed 8 people.
- Rice is sold in packets of 2 kg. How many packets will he need for the meal? (1)
- If rice costs R 31,50 per 2 kg pack, calculate the total cost of the rice he will need. (1)
- If beef costs R 41,75 per kg, calculate the total cost of the beef needed for the (1)
- Calculate the total cost of the rice and the (1) [4]
Solutions
- 2 ✓
- R63,00 ✓
- R62,63 ✓
- R125,63 ✓
4.4 Measuring volume and capacity
Volume is a measurement of how much space an object takes up. Capacity is a measure of how much liquid a container can hold when it is full.
For example, if you have a 500 mℓ bottle of cola, with 200 mℓ of cola left inside it, the capacity of the bottle is 500 mℓ, while the volume of cola inside it is 200 mℓ.
e.g. Worked example 7
An urn of boiling water in an office has a capacity of 20 litres.
- If it is filled to maximum capacity, calculate the number of 250 mℓ cups that can be shared from
- After everyone has had their morning tea, there are only 6 litres of water left in the
- How much water is this in mℓ?
- How many 250 mℓ cups of water are left in the urn now?
- What percentage is the remaining 6 litres of the urn’s capacity?
Solutions
- 20 litres = 20 000 mℓ
Then 20 000 mℓ ÷ 250 mℓ = 80
80 cups can be poured from the urn. - (i) 6 ℓ = 6 000 mℓ
(ii) 6 000 mℓ ÷ 250 mℓ = 24
There are 24 cups of water left in the urn.
(iii) 6 ℓ ÷ 20 ℓ × 100 = 30% The urn is 30% full.
e.g. Worked example 8
Jabu is building a new flower bed and is using a bucket to carry soil from another part of the garden to the new bed. He knows his bucket has a capacity of 10 ℓ.
- If 300 ℓ of soil must be moved, and for each trip Jabu fills the bucket to the top with soil, how many trips will Jabu have to make with the bucket to move all the soil?
- Jabu decides that 10 litres of soil is too heavy to How many trips will he have to make to move all the soil if he only fills the bucket with 7 litres of soil at a time?
- Jabu’s friend Matthew arrives with his wheelbarrow and a He suggests that Jabu should rather move the soil using the wheelbarrow. If the wheelbarrow has a capacity of 150 litres and they fill it to capacity, how many trips will Jabu have to make to move all the soil?
Solution
- 300 ℓ ÷ 10 ℓ = 30 trips
- 300 ℓ ÷ 7 ℓ = 42,8
Jabu can’t make 0,8 of a trip so we round this up to 43 trips (even though the bucket won’t have 7 litres of soil in it for the last trip). - 300 ℓ ÷ 150 ℓ = 2 trips
Jonathan uses the following recipe to make chocolate muffins:
- 2 cup of baking cocoa
3 - 2 large eggs
- 2 cups of flour
- 1 cup of sugar
2 - 2 teaspoons of baking soda
- 1 1 cups of milk
3 - 1 cup of sunflower oil
3 - 1 teaspoon of vanilla essence
- 1 teaspoon of salt
2
QUESTIONS
- If 1 teaspoon = 5 mℓ, calculate how much baking soda Jonathan will use. Give your answer in mℓ. (1)
- Calculate the amount of vanilla essence Jonathan will use in this Give your answer in mℓ. (1)
- Jonathan does not own measuring cups but he does own a measuring jug calibrated in mℓ. How many mℓ of flour does he need? (1 cup = 250 mℓ) (1)
- If Jonathan buys a 100 mℓ bottle of vanilla essence, how many times will he be able to use the same bottle, if he bakes the same amount of muffins each time? (1)
- The recipe above is used to make 30 muffins. Calculate how many cups of flour Jonathan will need to make 45 (1) [5]
Solutions
- 10 mℓ ✓
- 5 mℓ ✓
- 500 mℓ ✓
- 20 times ✓
- He will need 3 cups of ✓
e.g. Worked example 9
Suppose paraffin is sold at R7,80 per litre at the service station.
- How much will you pay for 5 litres of paraffin?
- How many litres of paraffin will you be able to buy for R20? Round off your answer to two decimal
- If you have a paraffin lamp at home that can hold 500 mℓ of paraffin, how many times will you be able to refill the lamp if you buy 3 litres of paraffin?
Solutions
- Number of litres × Cost per litre
= 5 litres × R7,80
= R39 - Amount of money ÷ Cost per litre
= R20 ÷ R7,80
= 2,564 102 56…
≈ 2,56 litres (to two decimal places) - 3 litres = 3 000 mℓ 3 000 mℓ ÷ 500 mℓ
= 6. You would be able to refill the lamp 6 times.
e.g. Worked example 10
Petrol costs R11,72 a litre.
- Calculate how much it costs to fill up a car that has a tank with a capacity of 50
- Calculate how many litres you could buy with Round off your answer to two decimal places.
Solutions
- Number of litres × Cost per litre
= 50 litres × R10,72
= R536 - Amount of money ÷ Cost per litre
= R200 ÷ R10,72
= 18,656 716 4…
≈ 18,66 litres (to two decimal places)
- Thandi is baking cupcakes and her recipe requires 11/3 cup of milk
1.1 Calculate how many mℓ of milk she will need if 1 cup = 250 mℓ. (1)
1.2 If the recipe is for 20 cupcakes, calculate the amount of milk required to bake 30 Give your answer in litres. (2)
1.3 Milk is sold in bottles of 1 litre for R8,50 at the local store. Calculate the amount of money Thandi will need to spend on milk to make the 30 (1)Solutions
1.1 333 mℓ of milk. ✓
1.2 She will need 500 mℓ of milk, ✓ which is 0,5ℓ. ✓
1.3 R8,50 (although she will only use half). ✓ Thabiso decides to sell homemade He has made 5 litres of lemonade to sell at the local schools’ rugby tournament.
2.1 Thabiso will be selling his lemonade in 250 mℓ plastic. Calculate the number of cups of lemonade he will be able to sell. (1)
2.2 If he sells the lemonade at R5 per cup, how much money will he make from the lemonade? (Assume that he sold all of his lemonade). (1)
2.3 If it cost Thabiso R120 to make the lemonade, how many cups would he need to sell (at R5 each) before he’s made back the money he spent? (1)
Solutions
2.1 20 cups ✓
2.2 R100 ✓
2.3 He would need to sell 24 cups just to cover his costs. ✓
4.5 Perimeter, area and volume
4.5.1 Estimation and direct measurement of perimeter
Perimeter is the total length of the outside of a shape or the continuous line forming the boundary of a closed geometric figure. Perimeter is calculated by adding together the lengths of each side of a shape. Perimeter is measured in mm, cm, m or km.
Perimeter formula | |
Rectangle |  |
Square | 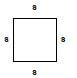 |
Triangle |
|
Circumference |
|
Note:
- To measure the perimeter of a rectangle, a square or a triangle, we simply measure the length of each side using a ruler and add up the sides to get the perimeter.
- To measure the perimeter of a circle, we need to use a piece of string: we can place the string along the outline of the circle, marking off how much string it took to go around the circle once. Then we measure that length of string on a ruler to estimate the perimeter of the circle.
The perimeter of a circle is the same as the circumference of the circle.
e.g. Worked example 11
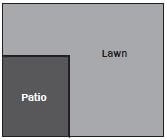
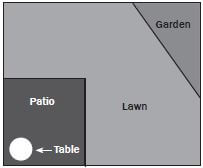
Mr and Mrs Dlamini have recently moved into a new house. In the rectangular back yard, the house has a lawn and a rectangular patio as shown in the diagram.
- Using a ruler, measure the perimeter (in cm) of Mr and Mrs Dlamini’s backyard on the diagram.
- If the diagram was drawn using a scale of 1 : 100, calculate the perimeter of the yard in metres.

Solutions
- The length of the yard is 5 cm and the width is 4,2
Because the back yard is a rectangle, both pairs of opposite sides are equal in length.
The perimeter is the total length of the outside of the yard, therefore: Perimeter = 4,2 cm + 4,2 cm + 5 cm + 5 cm
= 18,4 cm - Using the scale of 1 : 100 Perimeter = 18,4 cm × 100
= 1 840 cm
= 18,4 m
e.g. Worked example 12
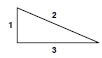
Mrs Dlamini wants to dig up some of the lawn and plant a triangular vegetable garden as shown in the diagram alongside.
- Using a ruler, measure the perimeter of the triangular garden in the diagram (in cm).
- If this diagram was drawn using a scale of 1 : 100, calculate the actual perimeter of the garden in metres.

Solutions
- The perimeter of the triangle is = 1,7 cm + 5 cm + 5,3 cm
= 12 cm - Using a scale of 1: 100
= 12 cm × 100
= 1 200 cm
= 12 m
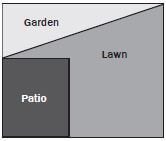
Activity 7: Measuring perimeter
Study the diagram alongside and answer the questions that follow.
- Before Mr Dlamini builds his fish pond, he decides he wants to make the patio smaller. Using a ruler, measure the new perimeter of the patio on the diagram (in cm). (1)
- Mrs Dlamini decides it might be better to build her vegetable garden on the right of the garden because that area gets more Using a ruler, measure the perimeter of the new triangular garden on the diagram (in mm). (1)
- Mrs Dlamini also buys a new, circular table for the Using a piece of string and a ruler, estimate the circumference of the table (in cm). (1) [3]

NB : You will always be given the perimeter formulae in your assessments.
Solutions
- approximately 10 cm ✓
- approximately 82 mm ✓
- approximately 2,5 ✓
Note:
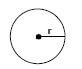
- The radius (r) of a circle is the length of the line from the centre of the circle to any point on its circumference.
- The diameter (d) of a circle is a straight line drawn from one edge of the circle to the other, that passes through the centre of the circle. diameter = 2 × radius.
- Pi (π) is a special symbol we use when calculating perimeter and area of circles. The value of π is 3,141 592 645…. For all of our calculations, we will use the approximate value of π = 3,142.
Worked example 13
Using the formulae given earlier, study the diagram alongside and answer the questions that follow.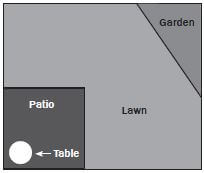
- Calculate the perimeter of the back yard, including the patio (i.e. the whole diagram) (in cm).
- Calculate the perimeter of the patio (in mm).
- Calculate the perimeter of Mrs Dlamini’s garden (in cm).
- Calculate the perimeter of the table on the patio (in cm). Round your answer to 1 decimal place.
- Is your answer to number d) different to the table circumference you estimated in the previous activity, using string and a ruler? If it is, discuss why this could be with a friend.
Solutions
- Perimeter of rectangular back yard
= 2 × length + 2 × width
= (2 × 6,2 cm) + (2 × 5,2 cm)
= 12,4 cm + 10,4 cm
= 22,8 cm - Perimeter of square patio
= 4 × length
= 4 × 2,5 cm
= 10 cm
10 cm × 10 = 100 mm - Perimeter of triangular garden
= length 1 + length 2 + length 3
= 2 cm + 2,9 cm + 3,5 cm
= 8,4 cm - Circumference of table
= π × diameter
= π × 0,8 cm
= 3,142 × 0,8 cm
= 2,5136 cm
= 2,5 cm - Previously, we estimated the circumference of the table using a piece of string and a ruler. Using the formula to calculate the circumference of a circle is more accurate than using a piece of string.
Note:
- The shapes we have worked with so far have been simple. Sometimes we have to calculate the perimeter of a more complicated shape, which is made up of regular shapes that have been joined together, or in which the units are not all the same. We will look at how to do this in the next activity.
Mrs Dlamini buys a new lampshade for a lamp. She measures the radius of the inside circle in the lampshade to be 50 mm. The diameter of the outside (larger) circle is 40 cm. (Note, the diagram is not drawn to scale.)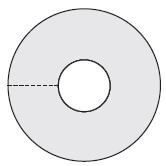
- Calculate the circumference of the smaller, inner circle (in cm). (3)
- Calculate the circumference of the larger, outer circle (in cm). Round off your answer to one decimal place. (3)
- Calculate the perimeter of half of the larger, outer circle (in cm). (1)
- Calculate the width of the area shown by the dotted line in the diagram (1) [8]
Solutions
- Inside circle perimeter/circumference
= 2πr ✓
= 2 × 3,142 × 5 cm ✓
= 31,42 cm ✓ - Circumference/perimeter
= 2πr ✓
= 2 × 3,142 × 20 cm ✓
= 125,7 cm ✓ Half perimeter
= Perimeter = 125,7 = 62,85 cm ✓
2 2Inner circle radius = 5 cm. Entire radius = 20 cm.
Difference between radii = 20 cm – 5 cm = 15 cm ✓ (1) [8]
4.5.2 Using formulae to calculate area
Area formula | Diagram |
Rectangle | 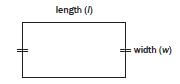 |
Square | 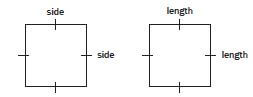 |
Triangle |
|
Circle |
|
- A perpendicular line is a straight line that lies at an angle of 90° to a given line,plane, or surface
e.g. Worked example 14
Using the appropriate formula from the given table, calculate the areas of the following three shapes (in cm2). Diagrams are not drawn to scale.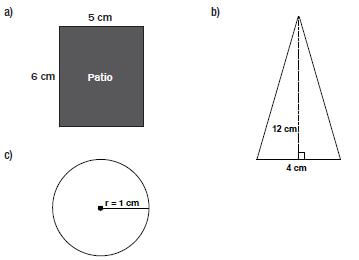
Solutions
- Area of rectangle = length × width
= 5 cm × 6 cm
= 30 cm2 - Area of triangle = ½ × base × perpendicular height
= ½ × 4 cm × 12 cm
= 24 cm2 - Area of circle = π × radius2
= 3,142 × (1 cm)2
= 3,142 × 1 cm2
= 3,142 cm2
In this case, it is easy to solve the problem by breaking down the complex object into smaller shapes, finding the area of each smaller shape, and then adding the individual areas together. The next worked example will show you how to work with such shapes.
e.g. Worked example 15
Your Mathematical Literacy classroom gets new tables, shaped as shown alongside.
- Using the appropriate formulae, calculate the area of the table, in m2.
- If each table cost R615 and ten tables were bought, calculate how much the tables cost per m2.
(Hint: calculate the total cost of the tables and their total area first.)
Solution
- We can see that the table is made up of two identical triangles, and one rectangle

The formula for the area of a triangle is:
½ × base × height
So the area of one of our triangles is:
½ × 0,5m × 0,7m (change the units to meters)
= 0,175 m2
The formula for the area of a rectangle is: length × breadth.
So the area of the middle rectangle is:
0,9 m × 70 cm
= 0,9 m × 0,7 m (change the units to metres)
= 0,63 m2
Now we simply add the three areas together:
Area triangle + area rectangle + area triangle
= 0,175 m2 + 0,63 m2 + 0,175 m2
= 0,98 m2 - 10 tables will cost R615 × 10 = R6
10 tables will have a total area of 0,98 m2 × 10 = 9,80 m2.
R6 150 ÷ 9,80 m2 = R627,55
So the tables cost R627,55 per square metre.
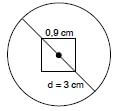
For your birthday, a friend gives you a rare, lucky coin that has a square cut out of the middle as shown in the photo and diagram.
- You measure the diameter of the circle to be 3 cm, and the length of one side of the square to be 0,9 cm. Calculate the area of the coin in cm2.
Round off your answer to one decimal place. (7)

- If the coin is worth R3,58 per cm2, calculate its value. (2) [9]
Solutions
- To calculate the area of the coin, we need to calculate the area of the circle, and then subtract from this the area of the square cut-out.
The formula for the area of a circle is π × radius2. ✓
We know the diameter is 3 cm, therefore the radius is 1,5 cm.
Therefore the area of the circle is:
π × (1,5 cm)2
= 3,142 × 2,25 cm2 ✓
= 7,0695 cm2. ✓
(Remember, we shouldn’t round off while we are still busy with our calculations! We should only round off our final answer.)
The formula for the area of a square is side × side = (side)2. ✓
Therefore the area of the square is:
(0,9 cm)2 = 0,81 cm2. ✓
We now subtract the area of the cut-out square from the area of the circle: 7,0695 cm2 – 0,81 cm2 = 6,2595 cm2 ✓
so the area of the coin is 6,2595 cm2 ≈ 6,3 cm2. ✓ (7) - 6,2595 cm2 × R3,58 ✓ = R22,409 01 ≈ R22,41 ✓ (2) [9]
4.5.3 Using formulae to calculate volume
Shape | Volume formula | |
Rectangular box | V = l × b × h |
|
Cylinder | V = π × r2 × h | |
e.g. Worked example 16
Cedric is building a house. First he digs the rectangular foundation for the house. The foundation is filled with cement. The dimensions of the foundation are 8 m × 0,5 m × 0,5 m.
- Calculate the volume of the foundation.
- If concrete for the foundation costs R180,00/m3, what is the total cost of the concrete for the foundation?
- Cedric finds cheaper concrete at a total cost of R320 for 2 m3. Calculate the cost per m3.
Solutions
- Volume = 8 × 0,5 × 0,5
= 2 m3 - Total cost of concrete = 2 × R180,00
= R360,00 - Cost per m3= R320,00 ÷ 2
= R160,00
Activity 10: Calculating volume
Allison needs to bake cookies for her son’s crèche. She finds a recipe for cookies. She needs to calculate the volume of 1 cookie so that she knows what size container she can use. Each cookie is shaped like a flat cylinder. She measures a cookie and finds that it has these dimensions: diameter = 80 mm; height = 7 mm.
- Calculate the volume of 1 biscuit, to one whole (3)
- Calculate the volume of 50 (1)
- Would a container with a volume of 700 cm3 hold the biscuits? (2) [6]
Solution
- 35 190 mm3 ✓
πr2h ✓
= π(40)2 (7) ✓
= π(1600) (7) - 1 759 500 mm3 ✓
- 1 759,5 cm3 (No 700 cm3 < 1 759,5 cm3) ✓✓
Activity 11: Multi-step volume problem
A school builds a swimming pool with the following dimensions: length = 15 m; depth = 1,3 m to the filling level, and width = 5 m.
(1 m3 = 1 000 ℓ and 1 000 ℓ = 1 kℓ)
- Calculate the volume of the swimming pool up to the level it is filled. (1)
- Convert this volume
(i) to litres
(ii) and kilolitres. (2) - When the school fills the pool, they use a pump which pumps water at a rate of 2 ℓ per second. How long would it take to fill up the pool? Give your answer in hours and minutes. (1)
- Water costs R8,64 per How much will it cost the school to fill up the pool? (1) [5]
Solutions
- 97,5 m3 ✓
- (i) 97 500 ℓ
(ii) 97,5 kℓ ✓✓ - So the total time taken is 13 hr 32½ min ✓
- R842,40 ✓
Elapsed time, or duration, is the measurement of time passing. When doing calculations like this, we add the units of time separately. Be careful when working with remainders!
e.g. Worked example 17
- School starts at 07:45. You are in class for 2 hours 30 What time will the bell ring for first break? Give your answer in the 24-hour format.
- Palesa starts cooking dinner at 6:00 m. She has to leave for her choir practice in 1 hour and 45 minutes.
- What time must she leave? (Give your answer in the 12-hour )
- Convert your answer to the 24-hour
- The bus leaves school at 14:30. It takes 70 minutes to get to Mulalo’s
- What time will he arrive at home? (Give your answer in the 24-hour )
- Convert your answer to the 12-hour
Solutions
- First add the hours: 07:00 + 2 hours = 9:00
Then add the minutes:
45 minutes + 30 minutes = 75 minutes
75 minutes = 60 minutes and 15 minutes
= 1 hour and 15 minutes
Calculate the total time elapsed:
9:00 + 1 hour 15 minutes = 10:15
So the bell will ring for break at 10:15. -
- First add the hours: 6:00 m. + 1 hour = 7:00 p.m.
Then add the minutes: 0 minutes + 45 minutes = 45 minutes
Calculate the total time that will elapse: 7:00 p.m. and 45 minutes
= 7:45 p.m.
So Palesa must leave at 7:45 p.m. - To convert this to the 24-hour time format we simply add 12 hours to the time:
7:45 p.m. + 12 hours = 19:45.
- First add the hours: 6:00 m. + 1 hour = 7:00 p.m.
-
- First we break down 70 minutes into hours and minutes
We know that 60 minutes = 1 hour. 70 minutes - 60 minutes = 10 minutes, so the bus ride takes 1 hour and 10 minutes.
Now we add the hours:
14:00 + 1 hour = 15:00.
Next we add the minutes: 30 + 10 = 40 minutes.
So Mulalo will arrive home at 15:40. - To convert our answer to the 12-hour format we subtract 12 hours:
15:40 – 12 hours = 3:40. We know that 15:40 is after midday, so Mulalo will arrive home at 3:40 p.m.
- First we break down 70 minutes into hours and minutes
Activity 12: Calculating elapsed time
- Unathi’s father goes to work at 8:00 m. He fetches her from school 7 hours and 30 minutes later. What time will he fetch her? Give your answer in the 24-hour format. (1)
- Lauren finishes her music class at 15:30. It takes her 30 minutes to get home. She then does homework for 50 minutes. Lauren meets her friend 20 minutes after she finishes her What time do they meet? Give your answer in the 12-hour format. (1)
- Heather starts baking biscuits at 6:15 p.m. The biscuits must come out of the oven at 6:35 m. and need to cool for another 20 minutes before they can be eaten.
- How long will the biscuits be in the oven? (1)
- What time will they be ready to eat? (Give your answer in the 12-hour format.) (1)
- Alison’s favourite TV show starts at 20:35. It is forty-five minutes long.
- What time will it finish? (1)
- If Alison watches the movie that follows her favourite show and it finishes at 10:50 p.m., how long was the movie (in hours and minutes)? (1)
- Vinayak is meeting his brother for lunch at 13:15. He also wants to go to the shops before It will take him 20 minutes to get from the shops to the restaurant where he’s meeting his brother. If he leaves home at 10:10 how much time does he have to do his shopping? Give your answer in hours and minutes. (1) [7]
Solutions
- 15:30 ✓ (1)
- 5:10 p.m. ✓ (1)
-
- 20 minutes✓ (1)
- 6:55 p.m. ✓ (1)
-
- 21:20 ✓ (1)
- 1 hour, 30 minutes ✓ (1)
- 2 hours, 45 minutes ✓ (1)
Calendars are useful tools to help us keep track of events that are going to happen and to plan our lives accordingly. We can add information to them about important events and dates (like birthdays and school holidays). We can read off days, weeks and months on a calendar and do conversions between these units of time.
You may have come across a time conversion that states that 4 weeks is approximately equal to one month. This is not quite correct. 4 weeks is equal to 28 days, but the months (except February!) have 30 or 31 days in them. When working with calendars, be careful to count the right number of days in a particular month!
e.g. Worked example 18
Jess’s calendar for the month of May is given below. Study it carefully and answer the questions that follow.
- If it is Monday 6 May, calculate how many days it is until:
- Mother’s Day
- Jess goes on her school camp
- Jess’s granny comes to
- If it is 8 May:
- How many weeks does Jess have to study for her Mathematical Literacy test?
- How many days does she have to study for the test?
- How many days ago was her dad’s birthday?
- Will Jess go to school on 1 May? Give a reason for your answer.
- Jess needs to buy a present for her mother for Mother’s If she has plans with friends on 11 May, by when should she have bought the present?
- Jess is invited to a party on Saturday 18 Will she be able to attend?
- Jess wants to bake a cake for her granny but has plans with a friend for the morning of 25
- If her granny arrives in the evening of 25 May, when should Jess bake the cake?
- Given that she’s busy on the morning of 25 May, when should Jess make time to buy the ingredients for the cake?
Solutions
- (i) 6 days
(ii) 11 days
(iii) 19 days - (i) 2 weeks
(ii) 14 days
(iii) 6 days ago - 1 May is Workers’ Day which is a public holiday.
- Jess should buy a present for her mother by Friday 10 May.
- She will be away on her school camp.
- (i) On the afternoon of Saturday 25 May.
(ii) On or before Friday 24 May.
Timetables are similar to calendars in that they help us plan our time. Where calendars are useful for planning months and years, timetables are useful for planning shorter periods of time like hours, days and weeks. You may already be familiar with timetables like those for your different classes at school, and for TV shows. In this section we will learn how to read timetables and how to draw up our own.
Worked example 19
Look at the timetable below and answer the following questions.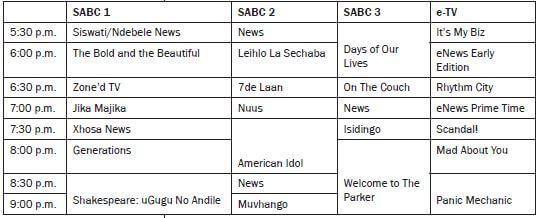
- What is the difference in time between the English News at 5:30 m. and the English News at 8:30 p.m. (both on SABC 2)?
- How long, in minutes, is American Idol?
- If Zonke wants to watch Isidingo after dinner at 7:30 m., and she needs 90 minutes to cook and eat dinner, what time should she start cooking dinner?
- Mandla wants to watch It’s My Biz and He plans to do his homework in between the two shows. If he expects each subject’s homework to take 30 minutes, how many subjects worth of homework will he be able to complete between the two shows?
- Sipho wants to watch the news in English and in Afrikaans, at the same Would this be possible? Give a reason for your answer.
- Why are the blocks on the timetable for SABC 3, blank for 8:30 m. and 9:00 p.m.?
- What is the total time period allocated to the News (in all languages) across all four TV channels?
Solutions
- 3 hours
- 7:30 to 8:30 m. = 1 hour = 60 minutes
- 90 minutes = 1 hour + 30 minutes
7:30 m. - 1 hour = 6:30 p.m.
6:30 p.m. - 30 minutes = 6:00 p.m. - It’s My Biz finishes at 6:00 m. and Generations starts at 8:00 p.m.
This gives Mandla 2 hours to do his homework.
2 hours = 120 minutes
120 minutes ÷ 30 minutes = 4
So Mandla will be able to do homework for four subjects in between the two shows - Yes, there is the English News on SABC 3 at 7:00 m. and on SABC 2 there is the Afrikaans Nuus at that same time.
However, he cannot watch two channels at the same time. He would need to choose a channel to watch. - They are blank because the program “Welcome to the Parker” is still showing.
- There are 8 sets of news slots appearing on the Each slot is 30 minutes. Therefore, a total of 4 hours of news will be shown between 5:30 p.m. and 9:00 p.m. on four channels.
Activity 13: Drawing up a timetable
Sipho and Mpho are brothers. Their parents require them to do household chores every day. These chores need to fit into their school sports and homework timetables.
Using the information provided in the table below, construct a timetable for each brother for one day of the week.
The two brothers’ timetables need to be clearly laid out and easy to read.
SIPHO | MPHO |
Soccer practice 15:30 - 16:30 | Music lesson (1 hour) |
Feed the dogs | Walk the dogs for a minimum of 30 minutes |
Wash the dishes | Study for Maths test - 45 minutes |
Complete his Life Orientation task - 45 minutes | Set (and clear) the table before and after dinner |
Watch the news at 19:00 for his history assignment | Look through the newspaper for any information on natural disasters for his geography homework. |
Solution
For example:
Sipho:
Time | Event |
15:30 - 16:30 | Soccer practice |
18:00 | Feed dogs and wash dishes |
19:00 | Watch news for history assignment |
19:30 - 20:15 | Complete LO task |
Activity 14: Reading a time table
Mr Odwa and his family live in the informal settlement in Langa Township. Mr Odwa has two school going kids Zonke and Andile who are attending the school at Philippi High. Mrs Odwa is a school teacher at Mandalay Secondary, while Mr Odwa works in a construction company in Woodstock.
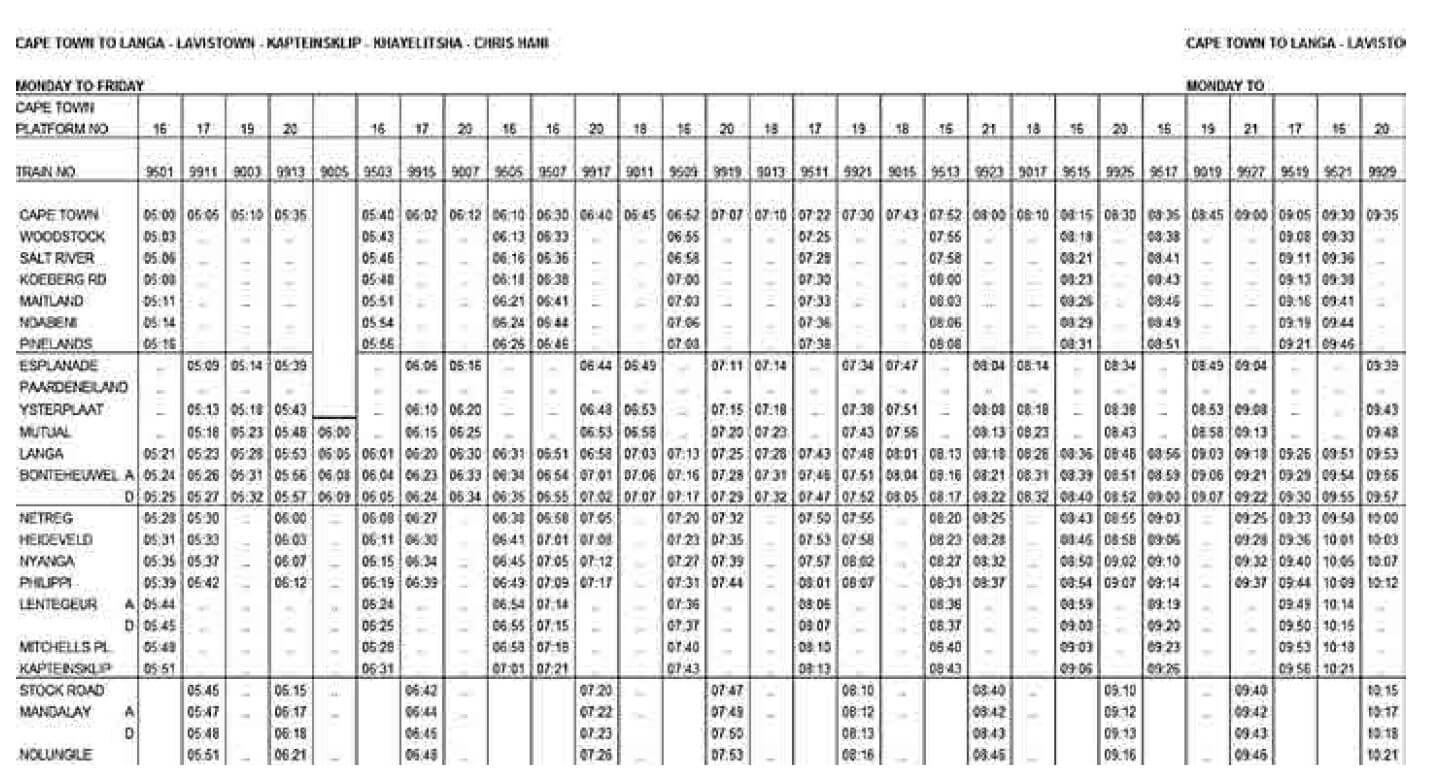
Use the train table on the previous page to answer these questions.
- If Zonke and Andile want to be at Philippi station at 07:31 what time must they catch a train in Langa station? (1)
- Which platform will that train depart from? (1)
- Give the train number and platform number for the train that will stop at Heideveld at 08:23. (2)
- If Mrs Odwa Pamela is at Mandalay at 09:12 what time did she depart from Langa station? (1)
- Mr Odwa works night shift and he wants to meet his two kids at Langa station before they catch their train to What time should he take the train in Woodstock and at which platform is that train going to stop? (2)
- If the school starts at 08:00 and the kids miss the train mentioned in 1, what time will be the next train and what number and platform must they be on to catch the train?(3)
- Is it possible for Mr Odwa to use the same time table to find the time for a train from Langa to Woodstock? Explain your answer. (2) [12]
Solutions
- 07:13 ✓ (1)
- 16 ✓
- Train number - 9513 ✓ (1)
Platform - 16 ✓ (2) - 8:48 ✓ (1)
- 6:33 (Platform 16 and Train 9507) ✓✓ (2)
- 7:25 on Platform 20 (Arrive in Philippi at 07:44) ✓✓✓ (3)
- No. The time table is one way from Cape Town to Chris Hani. ✓✓ (2) [12]