NUMBERS AND CALCULATIONS WITH NUMBERS GRADE 12 NOTES - MATHEMATICAL LITERACY STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupNumbers and calculations with numbers
- Using a calculator
- Common fractions
- Decimals
- Percentages
- Ratio, proportion and rate
- Activity 1: Working with ratio
- Rounding off according to the context
- Squares and cubes of numbers
- Time
- Activity 2: Convert units of time
1.1 Using a calculator
Basic calculators have a layout of keys similar to this: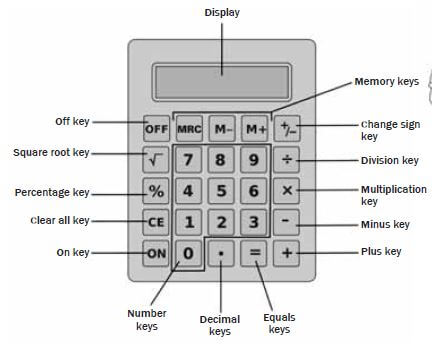
Note: Large numbers can look different on a calculator display, e.g. 24 900 can look like this:
24900 or 24’900.
Changing the sign of numbers
Practise changing the sign of a number on your calculator. For example, change100 to −100. Calculators usually have a [+/–] key, which changes the sign of a number.
Checking your calculations
Sometimes you may press the wrong button on a calculator and get the wrong answer.If you estimate quickly before doing the calculation, you may realise your answer is wrong, and then you can do the calculation again. It is easier to pick up a big mistake than a small one, e.g. you will notice a difference ifyou enter 67 instead of 657.Always do a calculation twice. If the two answers are different, you needto do it again. This is especially useful when you are adding long lists ofnumbers.Estimating means you make a rough calculation. It doesn’t mean you areguessing. An easy way to estimate is to round off the numbers and thendo the simpler calculation.In this case, you don’t have to round off to a certain digit. You can decidewhat number to round off to by looking at the calculation.We will revise rounding off in Section 1.6.
Worked Example 1
Estimate and then calculate:
- 467 – 93
- 6808 ÷ 74
Solutions
- 467 – 93
Estimate: 500 –100 = 400
Round off both numbers to the nearest 100.
Calculate: 467 – 93 = 374
374 is reasonably close to 400. - 6808 ÷ 74
Estimate: 7 000 ÷ 70 = 100
Calculate: 6 808 ÷ 74 = 92
BODMAS
If there are no brackets in a calculation, we use the BODMAS rule toremember in which order we must do the operations. This is a rule for thecorrect order: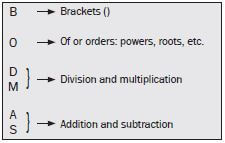
Worked example 2
40 000 – 2 000 × 3 = 34 000.
You must first multiply 2 000 by 3 and then subtract the answer from 40 000. There is no other way to do this calculation.If there are brackets, first do the operation in the brackets; then do the multiplication ordivision (from left to right); and last, do the addition or subtraction (from left to right).
Worked example 3
Kepa wrote this formula to show the cost of some clothes that he bought:
Cost = 4 + (R160 + 5) × R85
Work this out using the correct oredr of operations
Solution
Cost = 4 + (R160 + 5) × R85
= 4 + 14 025
= R14 029
Worked example 4
Work out (80 – 40 + 8) ÷ 4 × 2
Solution
(80 – 40 + 8) ÷ 4 × 2
= (40 + 8) ÷ 4 × 2
= 48 ÷ 4 × 2
= 12 × 2
= 24
1.2 Common fractions
A fraction is a measure of how something is divided into parts.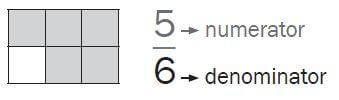
- This is called a common fraction. The numerator and the denominator are both whole numbers and they are separated by a line that represents division.
- Common fractions are called proper fractions when the numerator is smaller than the denominator, e.g. 2/10 or 3/5.
- When the numerator is bigger than the denominator, the fraction is called an improper fraction, e.g. 5/2 or 7/4.
- When we convert improper fractions to whole numbers with a fraction they are called mixed numbers, e.g. 9/2 = 41/2 and 4/3 = 11/3.
1.3 Decimals
What is a decimal fraction?
Think back to place value: Thousands; Hundreds; Tens and Units.
1 000÷10 = 100 |
100÷10 = 10 |
10÷10 = 1 |
1÷10 = 0,1 |
The number 0,1 is equal to 1/10 . This is how a basic calculator shows one tenth.
The bar below is divided into ten equal parts; 1 is divided into 10.![]()
We have found that 1 ÷ 10 = 0,1. Think back to fractions:
1 ÷ 2 = 0,5
So 1 ÷ 10 = 0,1
0,1 is just another way of writing 1/10 .
Place value
The value of a digit depends on its place in a number. For example, in 808,713 kg the first 8 is 800 kg and the second 8 is 8 kg.
Hundreds | Tens | Units | tenths | hundredths | thousandths |
8 | 0 | 8 | 7 | 1 | 3 |
Every digit has a place value 10× more than the digit on its right.
Worked example 5
- Write these numbers in a place value table.
Hundreds | Tens | Units | tenths | hundredths | thousandths |
- 30,44
- 302,404
Hundreds | Tens | Units | tenths | hundredths | thousandths |
3 | 0 | 4 | 4 | ||
3 | 0 | 2 | 4 | 0 | 4 |
Hint:
Another trick to keep in mind is how we multiply numbers by 10, 100 and 1 000.
- To multiply by 10, every digit moves to the left by one decimal place, OR the decimal comma moves to the right once.
- To multiply by 100, every digit moves to the left by two decimal places, OR the comma moves to the right twice.
- To multiply by 1 000, every digit moves to the left by three decimal places, OR the comma moves to the right three times.
It is useful to do these calculations in a place value table, or in columns.
Worked example 6
Look at the example in the place value table below. We multiply the number 287,5 by 10, then 100 and then 1 000.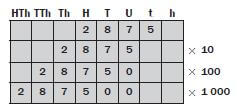
1.4 Percentages
To solve a percent problem, first identify the three parts in the calculation. Two of the parts should be given, and you need to calculate the third part.
Types of percent problems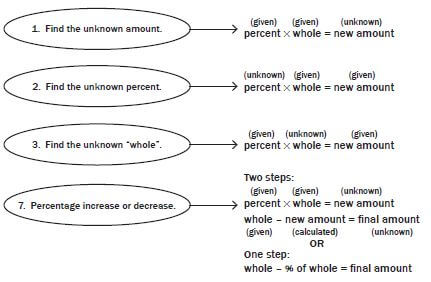
Type 1: Find the unknown amount
If you know the whole and the percent, you need to find the unknown amount.
Note:
The rule: Percent ´ whole = new amount
Worked example 7
What is 18% of 300?
Solution
Write the equation: 18% × 300 = new amount
18 × 300 = new amount
100
54 = new amount
Hint:
"OF" means "multiply"
Type 2: Find the unknown percent
- If the amount is less than the whole, the percent will be less than 100%.
- If the amount is greater than the whole, the percent will be greater than 100%.
Worked example 8
A group of 30 out of 150 learners represents the Grade 12s in athletics. What percentage is this?
Solution
We know the amount, 30, and the whole,150. The percent is the unknown.
Write an equation: percent × whole = amount
30 = 0,2 × 100 percent
150
Divide both sides by 150: percent = 20%
Type 3: Find the unknown whole
Worked example 9
You get 40% for a test, or a mark of 28. What is the total number of marks for the test?
Solution
We know the amount, 28, and the percent, 40%. The whole (total marks) is the unknown.
Write an equation: percent × whole = amount
40% × whole = 28
40 × whole = 28
100
0,4 × whole = 28
Divide both sides by 0.4: whole = 28
0,4
whole = 70
28 marks is 40% of 70 marks.
The total for the test is 70 marks.
Type 4: Percentage increase or decrease
These kinds of problems combine ordinary percent problems with final addition or subtraction.
RULE:
new amount = whole + (percentage × whole)
Percentage added to an amount (Percentage increase)
Percentage increase on a price means the normal price plus the increase.
Worked example 10
The price of petrol increases by 12%. The original price was R10,70 per litre. What is the new petrol price?
Method 1
New price = old price + 12% of old price
New price = R10,70 + 12% × R10,70
= R10,70 + 0,12 × R10,70
= R10,70 + R1,284
= R11,984
which is R11,98
Method 2
New price = old price + 12% of old price
= 112% of old price
= 1,12 × old price
= 1,12 × R10,70
= R11,98
Worked example 11
Nomalizo receives a salary increase of 7%. If her new salary is R10 600, what was her salary before the increase?
New salary = original salary + 7% of original salary
R10 600 = (100% + 7%) of original salary
R10 600 = 107% × (original salary)
R10 600 = original salary
107%
So the original salary is R9 907.
Percentage taken away from an amount (Percentage decrease)
Percentage decrease on a price means the normal price less the decrease.
RULE:
new amount = whole – (percentage × whole)
Worked example 12
A pair of jeans is on sale with a mark down of 20%. If the original price of the jeans was R199,00, what is the sale price?
Method 1
Discount = 20% × R199
= 0,2 × R199
= R39,80
The sale price = original price – discount
= R199 – R39,80
= R159,20
Method 2
Sale price is normal price less 20%, so sale price is 80% of normal price.
Sale price = 80% of R199
= 0,8 × R199
= R159,20
Working with VAT
All prices that we see in shops include VAT (Value Added Tax). You need to calculate VAT when:
- you are selling something and have to add VAT to the price
- you want to check an invoice and make sure that the correct amount of VAT is included
- VAT-inclusive: means that 14% VAT has already been added to the price
- VAT-exclusive price + amount of VAT = the price including VAT.
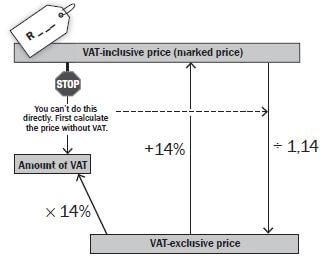
Worked example 13 Write down three digits after the decimal comma from your calculator so that you can round off. | Worked example 14 |
1.5 Ratio, proportion and rate
1.5.1 Ratio
Ratios are used in many kinds of calculations and problems. Ratios compare values.
A ratio says how much of one thing is compared to another thing. Here are 3 grey squares to 2 white squares: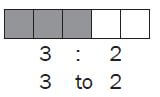
Ratios can be shown in different ways:
Use “:” to separate the values: 3 : 2
Instead of “:” you can use the word “to”: 3 to 2
or write it as a fraction: 3/2
Ratios can be scaled up or down: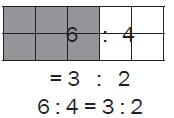
The ratio 6 : 4 is the same as 3 : 2, even though there are more squares in total.
The trick with ratios is to always multiply or divide both of the numbers by the same value.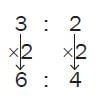
3 : 2 is the same as 3 × 2 : 2 × 2 = 6 : 4.
Writing ratios in the simplest form and equal ratios
You can write a ratio in its simplest form in the same way as you would write a fraction in its simplest form. Check if there is a number that divides into both numbers, starting with the smallest number in the ratio, and then checking with 2; 3; 5; etc. If there is none, then the ratio is already in its simplest form.
To check if ratios are equivalent write both of them in their simplest form, which will be exactly the same if they are equal. For example 5 : 10 and 30 : 60 are equivalent ratios because they both simplify to 1 : 2.
Worked example 15
A recipe for pancakes uses 3 cups of flour and 2 cups of milk. So the ratio of flour to milk is 3 : 2.
If you need to make pancakes for many people you might need 4 times the quantity, so you multiply both of the numbers by 4:
3 × 4 : 2 × 4 = 12 : 8
12 cups of flour and 8 cups of milk.
The ratio is still the same
Worked example 16
If there are 80 learners who travel by bus and 120 learners who travel by taxi, then we have a ratio of 80 (bus) to 120 (taxi). What is this ratio in its simplest form?
80 : 120
means the same as 8 : 12 (divide both numbers by 10)
which means the same as 2 : 3 (divide both numbers by 4)
Activity 1: Working with ratio
A company has a total of 150 employees and 25 of them are managers.
What is the ratio of managers to non-managers?
- 1 to 3
- 1 to 4
- 1 to 5
- 1 to 6
- 2 to 5 [5]
Solution
The company has 25 managers✓, so the remaining 125 employees are non-managers.✓
Express this ratio as a fraction and then reduce it:
Managers = 25 = 1 ✓
Non-managers 125 5
3The ratio of managers to non-managers is 1 to 5, so the correct answer is Choice (C) ✓✓. [5]
1.5.2 Ratios that compare 3 numbers
Sometimes 3 quantities are mixed together in a fixed ratio. You work with these ratios in the same way.
Worked example 17
A grandmother wants to share R800 between her three grandchildren, in the ratio of their ages 20 years, 15 years and 5 years. How much should they each get?
Solution
Simplify the ratio 20: 15: 5
= 4: 3: 1
The total number of parts is 4 + 3 +1 = 8
The shares are:
- 4 × R800 = R400
8 - 3 × R800 = R300
8 - 1 × R800 = R100
8
The shares add up to R800
1.5.3 Different kinds of problems to solve with ratios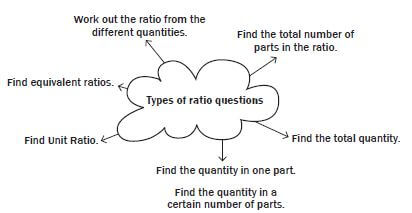
Find a missing number.
1.5.4 Writing ratios in unit form
Writing a ratio in the simplest form will sometimes result in one of the numbers being equal to 1. This is called a unit ratio. For example, the ratio of 5 roses to 15 daisies in a bunch of flowers is simplified to the unit ratio 1 : 3.
In some situations a unit ratio is not in the simplest form. For example, 5 : 9 can be written as 1 : 1,8, which is a unit ratio, but is not in the simplest form. To calculate the unit ratio, we simply divide both numbers by the smaller number, so 5 ÷ 5 : 9 ÷ 5 =1 : 1,8.
Let’s look at some situations in which the unit ratio is useful.
Worked example 18
- There are 23 nurses in a hospital and 7 567 patients. How many patients does each nurse have to care for?
- In a Grade 10 class, learners are voting for a class badge. 4 learners vote for badge A and 17 vote for badge B. How many learners vote for badge B for each learner voting for badge A?
Solutions
- 23 : 7 567
= 1 : 329
Each nurse must care for 329 patients. - Learners voting for badge B = 17 and learners voting for badge A = 4. 17: 4
= 4,25 : 1
Approximately 5 learners vote for badge B for each learner who votes for badge A.
Proportions
A proportion is an equation with a ratio on each side. It is a statement that two ratios are equal.
1 = 5 is an example of a proportion.
20 100
When one of the four numbers in a proportion is unknown, we can cross- multiply to find the unknown number. We can use question marks, place- holders (□) or letters in place of the unknown number.
Worked example 19
Sipho is making up bunches of flowers to sell at a flower shop. He is instructed to use three times as many daisies as roses in each bunch.
So the ratio of roses to daisies is 1: 3.
He has 15 daisies in one bunch. How many roses should he put in this bunch? We don’t know how many flowers there are in the bunch altogether.
Solution
Write the problem as a proportion. Here is a proportion with ? standing for the unknown number:
1: 3 = ?: 15
Or 1 = ?
3 15
The ? represents the number of roses he should put in.
There are many ways to find the unknown value. We can use what we know about equivalent fractions to make ?/15 the same as 1/3. We need to multiply the denominator 3 by 5 to get the denominator 15, so we would also have to multiply the numerator 1 by 5. So we get the fraction 5/15 .
Another way to find the value of the unknown is to cross-multiply.
1 = ?
3 15
1 × 15 = 3 × ?
15 = 3 × ?
We want to solve this equation by getting the unknown on its own on one side of the equation. So we divide both sides of the equation by 3 and we get:
5 = ?
This gives us the same answer.
So Sipho must use 5 roses and 15 daisies.
Notice that there are 20 flowers in this bunch. We did not need to use this fact to find the answer, because we knew the ratio and one number.
When we use ratio and proportion to solve problems, it is important to state very clearly which numbers represent which quantities. It can help to use tables for this.
In the example of the bunch of flowers above, we could have represented the information in a table like this:
Roses : daisies | 1 : 3 | ? : 15 |
Number of roses | 1 | ? |
Number of daisies | 3 | 15 |
Worked example 20
A summer camp has a boy-to-girl ratio of 8 :11. If the camp has 88 boys, what is the total number of children in the camp?
- 121
- 128
- 152
- 176
- 209
Solution
Begin by setting up the proportion as the following equation:
Boys = 8
Girls 11
Before continuing, notice that the ratio specifically mentions boys first and girls second, so this order is maintained in the equation. The camp has 88 boys, so substitute this number for Boys in the equation. You don’t know how many girls there are, so use the variable g. Here’s what your equation now looks like:
88 = 8
g 11
To find out how many girls are in the camp, solve for g using algebra. First, cross- multiply to get rid of the two fractions:
88(11) = 8(g)
968 = 8g
Now divide both sides by 8:
121 = g
The camp has 121 girls and 88 boys, so you know it has a total of 209 children; therefore, the correct answer is Choice (E).
1.5.5 Rate
What is a rate?
A rate, like a ratio, also compares two numbers or measurements, but the two numbers in a rate have different units.
Some examples of rate include cost rates, (for example potatoes cost R16,95 per kg or 16,95 R/kg) and speed (for example, a car travels at 60 km/h).
When we calculate a rate, we divide by one of the values, so we are finding the amount per one unit, which is a unit rate.
One example of a unit rate is speed in km/h.
If a car’s speed is 60 (km/h) kilometres per hour, then for every hour of driving, a distance of 60 km is covered.
If we want a unit cost rate for R20 for 2 kg of flour, we write:
R20 : 2 kg = R10 : 1 kg
= R10/kg.
This rate is a unit rate.
1.6 Rounding off according to the context
When we round off numbers, we need to be aware of the context of the problem. This will determine whether we round up or down.
When we round off to the nearest 10, we follow the simple rule that numbers with unit digits from 1 to 4 are rounded down to the lower ten, while numbers with units digits from 5 to 9 are rounded up to the higher ten.
However, when we are working in some practical, real-life situations, we must think carefully about the effect of rounding off. In other words, the answer must be reasonable so that it is not only correct, but also makes sense in the situation.
For example, South Africa no longer has 1c and 2c coins, so shops need to round off the totals to a 5c value if customers are paying cash. Shops round down, rather than rounding up. So if your total is R13,69, you would pay R13,65 in cash. If you pay by credit or debit card however, the totals are not rounded off.
Worked example 21
Answer the following questions and in each case explain why you would round up or down to get a reasonable answer.
- Jacolene is catering for a group of 54 people. The muffins are sold in packs of 8. How many packs of muffins must she buy?
- A group of learners is going to the Maropeng Centre at the Cradle of Humankind. There are 232 learners and teachers going on the outing. The school needs to hire buses and each bus can carry 50 passengers.
- How many buses should they hire?
- How many empty seats will there be?
- Ludwe is buying blinds for a large window in his home. Each blind is 100 cm wide. The window is 260 cm wide. How many blinds does he need?
Solutions
- Number of packs = 54
8
= 6,75
She must buy 7 packs. -
- Number of buses = 232
50
= 4,64
The school will need 5 buses. - Number of empty seats = 250 – 232
= 18 empty seats
- Number of buses = 232
- Number of blinds needed = 260
100
= 2,6
He needs 3 blinds.
1.7 Squares and cubes of numbers
Squares of numbers
The square of a number is the number multiplied by itself.
42 means ‘4 squared’ or 4 × 4.
We can represent squares of numbers in diagrams. The number of blocks along one side of the square is the number that is being squared. The total number of small squares in each diagram is equal to the square of the number.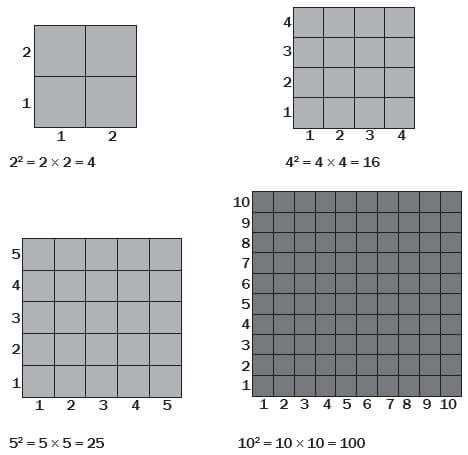
You need to know how to square numbers in order to work with area.
Square roots
In each example above, the number that is squared is the square root of the answer. So the square root of 42 is equal to 4. We can write this as
√16 = 4. Similarly √25 = 5, and √100 = 10.
To work out square roots on your calculator: enter the number, and then use the square root key.
Finding the square root of a number is the same as finding the side of the square. It is the opposite of squaring the number.
Cubes of numbers
In the same way, a number to the power of three is called the cube of the number. So 33 is 3 × 3 × 3, or ‘three cubed’ and is equal to 27. In the diagram below, the length of each side is the number that is cubed.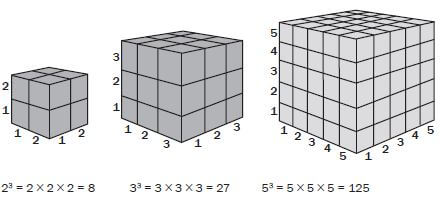
1.8 Time
Time values can be expressed in different formats, e.g. 8 o’clock, 8:00 a.m., 8:00 p.m. and 20:00.The two most common formats are the 12-hour format and the 24-hour format.
12-hour format: 8:00 a.m. and 8:00 p.m. are examples of readings of time using the 12-hour format. This format is seen on analogue clocks and watches. In the diagram below, the short hand shows us the hour and the long hand shows us the minutes. Sometimes a third hand shows the seconds.
When we use the 12-hour clock, we use the letters “a.m.” to show that the time is before midday (12 o’clock or noon) and “p.m.” to show that it is after midday. For example, school may start at 7:30 a.m. (in the morning) and finish at 2 p.m. (in the afternoon).
24-hour format: 20:00 is an example of the 24-hour time format. This format is seen on digital watches, clocks and stopwatches. On digital clocks, the number on the left shows the hour and the number on the right shows the minutes. Some digital watches have a third, smaller number on the far right which shows seconds.
Sometimes we also speak of “hundred hours format”. In “hundred hours” time format, we replace the colon (:) with an “h”, so, 20:00 is written 20h00.
Worked example 22
- Write the following times in the 24-hour format.
- Jane goes to bed at 9:56 p.m.
- The local shop opens at 8:30 a.m.
- Archie’s cricket practice ends at 4:05 p.m.
- Write the following times in the 12-hour format.
- David’s school day ends at 14:45.
- Mrs Gwayi has morning tea at 10:25.
- The Dube family eats dinner at 19:35.
Solutions
-
- 09:56 + 12 hours = 21:56
- 8:30 (This is before midday so it’s written the same.)
- 4:05 p.m. + 12 hours = 16:05
-
- 14:45 – 12 hours = 2:45 p.m.
- 10:25 a.m. (This is before midday so it’s written the same.)
- 19:35 – 12 hours = 7:35 p.m.
Converting units of time
The relationships between the units of time are given in the table below.
Time Conversions |
60 seconds = 1 minute |
60 minutes = 1 hour |
24 hours = 1 day |
7 days = 1 week |
365 days = approximately 52 weeks = 12 months = 1 year |
Worked example 23
- It takes John 140 seconds to boil water in a kettle. How many minutes and seconds does the water take to boil?
- A movie lasts 138 minutes. How long is the movie in hours and minutes?
Solutions
- 60 seconds = 1 minute
Therefore 140 seconds = 140 = 2,33 ... This does not mean 2 minutes 33 seconds!!!
60
From our answer of 2,33 we know that we have 2 whole minutes and some remainder in seconds.
We can now work backwards to calculate the remainder:
2 minutes = 120 seconds
140 seconds – 120 seconds = 20 seconds
So 140 seconds = 2 minutes and 20 seconds. (0,33… × 60 = 20 sec.) - 60 minutes = 1 hour
Therefore 138 minutes = 138 = 2,3. This does not mean 2 hours and 3 minutes!
60
We know that we have 2 whole hours and some remainder in minutes. We now work backwards to calculate the remainder:
2 hours = 120 minutes
138 minutes - 120 minutes = 18 minutes
So 138 minutes = 2 hours and 18 minutes. (0,3 × 60 = 18 minutes)
Activity 2: Convert units of time
- A train journey takes 34 hours. How many days and hours does the journey take? (3)
- A plane trip (with stopovers) from South Africa to China takes 38 hours. How many days and hours does the trip take? (1) [4]
Solutions
|