MATHEMATICAL LITERACY OVERVIEW GRADE 12 NOTES - MATHEMATICAL LITERACY STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupOVERVIEW
MATHEMATICAL LITERACY
STUDY GUIDES AND NOTES
GRADE 12
- Overview of the grade 12 exam
- How to use this study guide
- Study skills to boost your learning
- Question words to help you answer questions
- Vocabulary
- The maths you need
Dear Grade 12 learner
This study guide helps you to prepare for the end-of-year CAPS Life Sciences Grade 12 exam.
The study guide does NOT cover the entire CAPS curriculum, but it does focus on core content of each knowledge area and points out where you can earn easy marks.
You must work your way through this study guide to improve your understanding, identify your areas of weakness and correct your own mistakes.
To ensure a good pass, you should also cover the remaining sections of the curriculum using other textbooks and your class notes.
OVERVIEW OF THE GRADE 12 EXAM
The following topics make up each of the TWO exam papers that you write at the end of the year:
TERM | GRADE 12 | |
1 | Control Test | |
2 | Paper 1 2 hours (100 marks) | Paper 2 2 hours (100 marks) |
3 | Control Test | Control Test |
Paper 1 3 hours (150 marks) | Paper 2 3 hours (150 marks) | |
4 | External Examinations | |
Paper 1 3 hours (150 marks) | Paper 2 3 hours (150 marks) | |
PAPER 1 | PAPER 2 | |
Intention | Basic skills’ paper → assesses proficiency of content and/or skills | Applications’ paper → assesses ability to use both mathematical and non- mathematical techniques/considerations to explore familiar and unfamiliar contexts. |
Structure and | 5 questions | 4 or 5 questions |
scope of content and/or skills | Four questions deal with contexts relating to each of the topics:
Fifth question integrates content from across all of these topics. | Each question deals with contexts drawing integrated content from across all of the topics:
Likelihood will be examined in the context or one or more of the other questions. |
Level 1 | 60% | |
Level 2 | 35% | 25% |
Level 3 | 5% | 35% |
Level 4 | 40% | |
Contexts | Familiar’, i.e. limited to the contexts listed in the CAPS document. | Both ‘familiar’ and ‘unfamiliar’, i.e. not limited to the contexts listed in the CAPS document. |
Topic | Weighting (%) | |
Basic skills topics | Interpreting and communicating answers and calculations | No weighting is provided for these topics. Rather, they will be assessed in an integrated way throughout the Application Topics. |
Numbers and calculations with numbers | ||
Patterns, relationships and representations | ||
Application topics | Finance | 35% (±5%) |
Measurement | 20% (±5%) | |
Maps, plans and other representations of the physical world | 15% (±5%) | |
Data handling | 25% (±5%) | |
Likelihood | Minimum 5% |
The four levels of the Mathematical Literacy assessment taxonomy | GRADE 12 | ||
PAPER 1 | PAPER 2 | OVERALL ALLOCATION | |
Level 1: Knowing | 60% ± 5% | 30% ± 5% | |
Level 2: Applying routine procedures in familiar contexts | 35% ± 5% | 25% ± 5% | 30% ± 5% |
Level 3: Applying multi-step procedures in a variety of contexts | 5% | 35% ± 5% | 20% ± 5% |
Level 4: Reasoning and reflecting | 0 | 40% ± 5% | 20% ± 5% |
How to use this study guide
This study guide covers selected parts of the different topics of the CAPS Grade 12 Life Sciences curriculum in the order they are usually taught during the year. The selected parts of each topic are presented in the following way:
- An explanation of terms and concepts;
- Worked examples to explain and demonstrate;
- Activities with questions for you to answer; and
- Answers for you to use to check your own work.
- A checklist from the exam guidelines for Life Sciences has been provided on page xvii for you to keep track of your progress. Once you have mastered the core concepts and have confidence in your answers to the questions provided, tick the last column of the checklist.
- The activities are based on exam-type questions. Cover the answers provided and do each activity on your own. Then check your answers.
Reward yourself for the things you get right. If you get any incorrect answers, make sure you understand where you went wrong before moving on to the next section. - In Chapter 12, you will find a section on graphing skills which you must master when preparing for both Paper 1 and Paper 2. This chapter also provides guidelines on how to answer essay-type questions in the exam.
- You will be asked to draw a labelled diagram in the exam. On page 115 to 132 are a set of blank diagrams that you can use to practise your drawing and labelling skills. Filling in these blank diagrams is a good way to test yourself and work out what you know well and what you still need more practice in.
- Use this study guide as a workbook. Make notes, draw pictures and highlight important concepts.
- Exemplar Exam papers are included in the study guide for you to do. Check your answers by looking back at your notes and the exam memoranda. Past exam papers go a long way in preparing you for what to expect and help reduce exam anxiety. Go to https://www.elimuza.com/ to download past exam papers.
Top 10 study tips
- Have all your materials ready before you begin studying - pencils, pens, highlighters, paper, etc.
- Be positive. Make sure your brain holds on to the information you are learning by reminding yourself how important it is to remember the work and get the marks.
- Take a walk outside. A change of scenery will stimulate your learning. You’ll be surprised at how much more you take in after being outside in the fresh air.
- Break up your learning sections into manageable parts. Trying to learn too much at one time will only result in a tired, unfocused and anxious brain.
- Keep your study sessions short but effective and reward yourself with short, constructive breaks.
- Teach your concepts to anyone who will listen. It might feel strange at first, but it is definitely worth reading your revision notes aloud.
- Your brain learns well with colours and pictures. Try to use them whenever you can.
- Be confident with the learning areas you know well and focus your brain energy on the sections that you find more difficult to take in.
- Repetition is the key to retaining information you have to learn.
Keep going - don’t give up! - Sleeping at least 8 hours every night, eating properly and drinking plenty of water are all important things you need to do for your brain. Studying for exams is like strenuous exercise, so you must be physically prepared.
Study skills to boost your learning
This guide includes 3 study techniques you can use to help you learn the material:
- Mobile notes
- Mnemonics
- Mind maps
Mobile notes
Mobile notes are excellent techniques will tools for learning all the key help you to study concepts in the study guide. smarter!
Mobile notes are easy to make and you can take them with you wherever you go:
- Fold a blank piece of paper in half. Fold it in half again. Fold it again.
- Open the paper. It will now be divided into 8 parts.
- Cut or tear neatly along the folded lines.
- On one side of each of these 8 bits of paper, write the basic concept.
- On the other side, write the meaning or the explanation of the basic concept.
- Use different colours and add pictures to help you remember.
- Take these mobile notes with you wherever you go and look at them whenever you can.
- As you learn, place the cards in 3 different piles:
- I know this information well.
- I’m getting there.
- I need more practice.
- The more you learn them, the better you will remember them.
Mnemonics
A mnemonic code is a useful technique for learning information that is difficult to remember.
Here’s the most useful mnemonic for Mathematics, Mathematical Literacy,and Physical Science:
B - Brackets
O - Of or Orders:powers,roots, etc
D - Division
M - Multiplication
A - Addition
S - Subtraction
Throughout the book you will be given other mnemonics to help youremember information.
The more creative you are and the more you link your ‘codes’ to familiarthings, the more helpful your mnemonics will be.
Mind maps
There are several mind maps included in this guide, summarising some of the sections.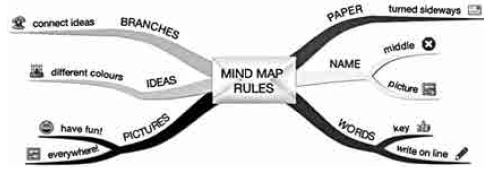
Mind maps work because they show information that we have to learn in the same way that our brains ‘see’ information.
As you study the mind maps in the guide, add pictures to each of the branches to help you remember the content.
You can make your own mind maps as you finish each section.
How to make your own mind maps:
- Turn your paper sideways so your brain has space to spread out in all directions.
- Decide on a name for your mind map that summarises the information you are going to put on it.
- Write the name in the middle and draw a circle, bubble or picture around it.
- Write only key words on your branches, not whole sentences. Keep it short and simple.
- Each branch should show a different idea. Use a different colour for each idea. Connect the information that belongs together. This will help build your understanding of the learning areas.
- Have fun adding pictures wherever you can. It does not matter if you can’t draw well.
On the day of the exam …
- Make sure you have all the necessary stationery for your exam, i.e. pens, pencils, eraser, protractor, compass, calculator (with new batteries). Make sure you bring your ID document and examination admission letter.
- Arrive on time, at least one hour before the start of the exam.
- Go to the toilet before entering the exam room. You don’t want to waste valuable time going to the toilet during the exam.
- Use the 10 minutes reading time to read the instructions carefully. This helps to ‘open’ the information in your brain. Start with the question you think is the easiest to get the flow going.
- Break the questions down to make sure you understand what is being asked. If you don’t answer the question properly you won’t get any marks for it. Look for the key words in the question to know how to answer it. A list of these words is on page xiv of this study guide.
- Try all the questions. Each question has some easy marks in it so make sure that you do all the questions in the exam.
- Never panic, even if the question seems difficult at first. It will be linked with something you have covered. Find the connection.
- Manage your time properly. Don’t waste time on questions you are unsure of. Move on and come back if time allows.
- Check weighting - how many marks have been allocated for your answer? Take note of the ticks in this study guide as examples of marks allocated. Do not give more or less information than is required.
- Write big and bold and clearly. You will get more marks if the marker can read your answer clearly.
Question words to help you answer questions
It is important to look for the question words (the words that tell you what to do) to correctly understand what the examiner is asking. Use the words in the table below as a guide when answering questions.
Question word | What is required of you |
Analyse | Separate, examine and interpret |
Calculate | This means a numerical answer is required – in general, you should show your working, especially where two or more steps are involved |
Classify | Group things based on common characteristics |
Compare | Point out or show both similarities and differences between things, concepts or phenomena |
Define | Give a clear meaning |
Describe | State in words (using diagrams where appropriate) the main points of a structure/process/phenomenon/ investigation |
Determine | To calculate something, or to discover the answer by examining evidence |
Differentiate | Use differences to qualify categories |
Discuss | Consider all information and reach a conclusion |
Explain | Make clear; interpret and spell out |
Identify | Name the essential characteristics PAY SPECIAL ATTENTION |
Label | Identify on a diagram or drawing |
List | Write a list of items, with no additional detail |
Mention | Refer to relevant points |
Name | Give the name (proper noun) of something |
State | Write down information without discussion |
Suggest | Offer an explanation or a solution |
Tabulate | Draw a table and indicate the answers as direct pairs |
Vocabulary
The following vocabulary consists of all the difficult words used in Mind the Gap Mathematical Literacy. We suggest that you read over the list below a few times and make sure that you understand each term. Tick next to each term once you understand it so you can see easily where the gaps are in your knowledge.
KEY | |
Abbreviation | Meaning |
(v) | verb: doing-word or action word, such as “walk” |
(n) | noun: naming word, such as “person” |
(adj) | adjective: describing word such as “big” |
(adv) | adverb: describing word for verbs, such as “fast” |
(prep) | preposition: a word describing a position, such as “on”, “at” |
(sing) | singular: one of |
(pl) | plural: more than one of |
(abbr) | abbreviation |
Term | Meaning |
A | |
abbreviate | (v). Make shorter. |
account for | (v). Explain why. |
adjacent | (adj). Next to something. |
analyse | (v). Examine something in detail. |
annotated | (adj). Something that has comments or explanations, usually written, added to it. |
ante- | (prep). Before (e.g., ante-natal – before birth) |
anti- | (prep). Against (e.g., anti-apartheid – against apartheid). |
approximate | (v. & adj.). Come close to (v); roughly, almost, not perfectly accurate, close but not exact. The verb is pronounced “approxi-mayt” and the adjective is pronounced “approxi-mitt”. |
arbitrary | (adj). Based on random choice; unrestrained and autocratic. |
C | |
category | (n). Class or group of things. |
consecutive | (adj). One after another without any gaps or breaks. |
consider | (v). Think about. |
contrast | (v). Thow the difference between; (n) something that is very different from what it is being compared with. |
conversely | (adv). The opposite of. |
D | |
data (pl), datum (sing) | (n). Information given or found. |
deduce | (v). To work something out by reasoning. |
deduction | (n). Conclusion or idea that someone has worked out. |
define | (v). Give the meaning of a word or words. |
definition | (n). The meaning of a word or words. |
denote | (v). To refer to or mean something. |
determine | (v). Work out, usually by experiment or calculation. |
E | |
elapse | (v). Pass by or finish, e.g., time. |
establish | (v). Show or prove, set up or create. |
exceed | (v). Go beyond. |
excess | (n). More than necessary. |
excluding | (prep). Not including. |
exclusive | (adj). Excluding or not admitting other things; reserved for one particular group or person. |
exemplar | (n). A good or typical example. |
exempt | (v). To free from a duty. |
exempt | (adj). Be freed from a duty. |
exemption | (n). Being freed from an obligation. |
extent | (n). The area covered by something. |
F | |
factor | (n). A circumstance, fact or influence that contributes to a result; a component or part. |
factory | (n). A place where goods are made or put together from parts. |
find | (v). Discover or locate. |
find | (n). Results of a search or discovery. |
finding | (n). Information discovered as the result of an inquiry. |
fixed | (adj). Not able to move, attached; or repaired, not broken. |
format | (n). Layout or pattern; the way something is laid out. |
G | |
global | (adj). Found all over the world (globe). |
I | |
identify | (v). Recognise or point out. |
illustrate | (v). Give an example to show what is meant; draw. |
imply | (v). Suggest without directly saying what is meant. |
indicate | (v). Point out or show. |
initial | (n). First. |
initiation | (n). The action of beginning something; the action of admitting somebody into a group or organisation. |
inter- changeable | (adj). Can be swapped or exchanged for each other. |
investigate | (v). Carry out research or a study. |
issues | (v). Comes out of. |
issues | (n). An important problem or a topic for debate. |
M | |
magnitude | (adj). Size. |
manipulate | (v). Handle or control (a thing or a person). |
motivate | (v). Give someone a reason for doing something. |
multiple | (adj). Many. |
N | |
negligible | (adj). Small and insignificant; can be ignored. From “neglect” (ignore). |
numerical | (adj). Relating to or expressed as a number or numbers. |
numerous | (adj). Many. |
O | |
obtain | (v). Get. |
optimal | (adj). Best; most favourable. |
optimum | (adj). Best; (n) the most favourable situation for growth or success. |
P | |
principal | (n). Head of a school. |
principal | (adj). Main or most important. |
principle | (n). A basic truth that guides the way a person behaves. |
priority | (n). Something that is considered to be more important or comes first. |
provide | (v). Make available for use; supply. |
Q | |
quality | (n). The standard of something compared to other similar things; a characteristic of someone or something. |
R | |
reciprocal | (adj). Given or done in return. |
record | (v). Make a note of something in order to refer to it later (pronounced ree-cord). |
record | (n). A note made in order to refer to it later; evidence of something; a copy of something (pronounced rec-cord. |
represent | (v). Be appointed to act or speak for someone; amount to. |
resolve | (v). Finalise something or make it clear; bring something to a conclusion. |
respect | (v). Admire something or someone; consider the needs or feelings of another person. |
respectively | (adj). In regards to each other, in relation to items listed in the same order. |
S | |
simul- taneously | (adv). At the same time. |
site | (n). Place. |
suffice | (v). Be enough. |
surplus | (adj). More than is needed. |
survey | (n). A general view, examination, or description of someone or something. |
survey | (v). Look closely at or examine; consider a wide range of opinions or options. |
T | |
tendency | (n). An inclination to do something in a particular way; a habit. |
tertiary | (adj). Third level. |
truncated | (adj). Cut short. |
U | |
under- reported | (adj). Not reported enough; there is not enough information. |
V | |
verify | (v). Show to be true; check for truth; confirm. |
vice versa | (adv). The other way round. |
versus | (prep). Against. Abbreviated “vs” and sometimes “v”. |
A | |
account | (n. & v.). Finance: A record of income and expenditure. To explain (v), e.g. “Account for why the sky is blue”. |
algebra | (n). A mathematical system where unknown quantities are represented by letters, which can be used to perform complex calculations through certain rules. |
angel | (n). In Abrahamic religions, a messenger from God. Note the spelling. |
angle | (n). The difference in position between two straight lines which meet at a point, measured in degrees. Note the spelling. |
annual | (adj). Once every year. (E.g. “Christmas is an annual holiday”). |
annum, per | (adv). For the entire year. (E.g. “You should pay R 100 per annum”). |
area | (n). Length x breadth (width). In common usage: a place. |
asset | (n). Something having value, which can be sold to defray (get rid of) debts. Can refer to physical things such as houses, cars, etc., or to savings and investments. |
ATM | (n). Abbreviation: automatic teller machine. |
average | (n). Mathematics: The sum of parts divided by the quantity of parts. In common use: neither very good, strong, etc., but also neither very weak, bad, etc; the middle. If you are asked to find the average, you always have to calculate it using the information you have. For example, the average of (1;2;3) is 2, because (1+2+3)/3 = 2. See also mean, median and mode. |
axis (sing), axes (pl, pronounced “akseez”) | (n). A line along which points can be plotted (placed), showing how far they are from a central point, called the origin. See origin. |
B | |
bias | (n). To be inclined against something or usually unfairly opposed to something; to not accurately report on something; to favour something excessively. |
BMI | (n). Body mass index. Calculated by dividing someone’s weight in kilograms by the square of his or her height in metres. An indication of whether someone is over- or underweight. |
BODMAS | (abbr.). Brackets, of/orders (powers, squares, etc), division, multiplication, addition, subtraction. A mnemonic (reminder) of the correct order in which to do mathematical operations. |
borrow vs lend | (v). To take something (e.g. money) from someone with their permission for temporary use (borrow). Lend means the opposite: it means to give money to someone for temporary use. Remember: Borrow from, lend to. Can refer to financial transactions. If you take money from a bank, you are the borrower and the bank is the lender. |
breadth | (n). How wide something is. From the word “broad”. |
budget | (n. & v.). To plan how to spend money (v); a plan of how to spend money (n); an estimate of the amount of money available (n). |
C | |
Cartesian | (adj). Anything believed or proposed by Rene Descartes. In particular, the x-and-y axis coordinate system. |
cash | (n). Printed or minted money, money not represented by cheques, cards, etc. |
cashier | (n). Person who receives payment. |
CFL | (n). Compact Fluorescent Light; a small fluorescent tube curled up inside a standard lightbulb shape. |
chance | (n). The same as possibility or likelihood; that something might happen but that it is hard to predict whether it will. |
chart | (v). To draw a diagram comparing values on Cartesian axes. |
cheque | (n). A bill issued by banks, and filled in by the drawer (the person writing it), to represent an amount owed, usually with place to state who the amount is due to. |
circum- ference | (n). The distance around the outer rim of a circle. |
compound interest | (n). Interest charged on an amount due, but including interest charges to date. Compare to simple interest. |
continuous | (adj). Mathematics: having no breaks between mathematical points; an unbroken graph or curve represents a continuous function. See function. |
control | (n. and v.). To ensure something does not change without being allowed to do so (v); an experimental situation to which nothing is done, in order to compare to a separate experimental situation, called the ‘experiment’, in which a change is attempted. The control is then compared to the experiment to see if a change happened. |
control variable | (n). A variable that is held constant in order to discover the relationship between two other variables. “Control variable” must not be confused with “controlled variable” (see independent variable). |
coordinate | (n). The x or y location of a point on a Cartesian graph, given as an x or y value. Coordinates (pl) are given as an ordered pair (x, y). |
correlate | (v). To see or observe a relationship between two things, without showing that one causes the other. |
correlation | (n). That there is a relationship between two things, without showing that one causes the other. |
correspond | (v). To pair things off in a correlational relationship. For two things to agree or match. E.g. A corresponds to 1, B corresponds to 2, C corresponds to 3, etc. |
credit | (n. & v.). To lend someone money |
cubed | (adj). The power of three; multiplied by itself three times. |
cubic | (adj). Shaped like a cube; having been multiplied by itself three times. |
cylinder | (n). A tall shape with parallel sides and a circular cross-section – think of a log of wood, for example, or a tube. See parallel. The formula for the volume of a cylinder is πr2h. |
D | |
debit | (v. & n.). When someone or an organisation takes money out of your account. Compare to withdraw. |
debt | (n). The state of owing money. |
deficit | (n). Excess spending, or, the difference between the amount owed and the amount paid; shortfall; the excess of expenditure (spending) or liabilities (debts) over income (earnings) or assets. |
denominator | (n). See divisor. In popular speech: a common factor. |
depend | (v). To be controlled or determined by something; to require something to happen or exist first. |
dependent (variable) | (adj/n). A variable whose value depends on another; the thing that comes out of an experiment, the effect; the results. See also independent variable and control variable. The dependent variable has values that depend on the independent variable, and we plot it on the vertical axis. |
deposit | (n). Finance: to place money into an account. |
derivation | (n). Mathematics: to show the working of your arithmetic or answer or solution; the process of finding a derivative. |
derivative | (n). Mathematics: The rate of change of a function with respect to an independent variable. See independent variable. In common use: something that comes from something else. |
diagonal | (adj. & n.). A line joining two opposite corners of an angular shape. |
diameter | (n). The line passing through the centre of a shape from one side of the shape to the other, esp. a circle. Formula: d = 2r. See radius, radii, circumference. |
difference | (n). Mathematics: subtraction. Informally: a dissimilarity. How things are not the same. |
dimension | (n). A measurable extent, e.g. length, breadth, height, depth, time. Physics, technical: the base units that make up a quantity, e.g. mass (kg), distance (m), time (s). |
distribution | (n). How something is spread out. Mathematics: the range and variety of numbers as shown on a graph. |
divisor | (n). The number below the line in a fraction; the number that is dividing the other number above the fraction line. See numerator, denominator. |
domain | (n). The possible range of x-values for a graph of a function. See range. |
E | |
element | (n). Mathematics: part of a set of numbers. Popular use: part of. |
elevation | (n). Science: height above the ground or sea level. Architecture: a face of a building as viewed from a certain direction on an architect’s plan of the building. See plan. |
eliminate | (v). To remove or get rid of. Mathematics: to cancel a factor out of one side of an equation by dividing by that factor throughout, or by substituting in another formula or value that is equal. |
expenditure | (n). How much money, time, or effort has been used on something. |
expense | (n). How much something costs in time, money, or effort. |
expensive | (adj). Using too much time, money or effort. |
exponent | (n). When a number is raised to a power, i.e. multiplied by itself as many times as shown in the power (the small number up above the base number). So, 23 means 2 x 2 x 2. See also cubed. |
exponential | (adj). To multiply something many times; a curve representing an exponent. |
extrapolation | (n). To extend the line of a graph further, into values not empirically documented, to project a future event or result. In plain language: to say what is going to happen based on past results which were obtained (gotten) by experiment and measurement. If you have a graph and have documented certain results (e.g. change vs time), and you draw the line further in the same curve, to say what future results you will get, that is called ‘extrapolation’. See predict. |
F | |
fraction | (n). Mathematics: Not a whole number; a representation of a division. A part. E.g. the third fraction of two is 0,666 or 2/3 . meaning two divided into three parts. |
frequency | (n). How often. |
function | (n). Mathematics: when two attributes or quantities correlate. |
fund | (n. & v.). A source of money (n); to give money (v). |
G | |
gradient | (n). A slope. An increase or decrease in a property or measurement. Also the rate of such a change. In the formula for a line graph, y = mx + c, m is the gradient. |
graph | (n). A diagram representing experimental or mathematical values or results. See Cartesian. |
graphic | (n., adj.). A diagram or graph (n). Popular use: vivid or clear or remarkable (adj.). |
graphically | (adv). Using a diagram or graph. Popular use: to explain very clearly. |
H | |
histogram | (n). A bar graph that represents continuous (unbroken) data (i.e. data with no gaps). There are no spaces between the bars. A histogram shows the frequency, or the number of times, something happens within a specific interval or “group” or “batch” of information. |
hyperbola | (n). Mathematics: a graph of a section of a cone with ends going off the graph; a symmetrical (both sides the same) open curve. |
hypotenuse | (n). The longest side of a right- angled triangle. |
I | |
incline | (n. & v.). Slope. See gradient (n); to lean (v). |
independent (variable) | (n). The things that act as input to the experiment, the potential causes. Also called the controlled variable. The independent variable is not changed by other factors, and we plot it on the horizontal axis. See control, dependent variable. |
inflation | (n). That prices increase over time; that the value of money decreases over time. General use: the action of getting bigger. |
informal sector | (n). Not part of the formal economy; street vendors or home workers; self-employed persons who have not formally registered a corporation or company but are manufacturing or selling items or work. |
insufficient | (adj). Not enough. |
insurance | (n). Finance: an agreement with an insurance company in which money is paid to guarantee against or compensate for future mishaps or losses. See premium. General use: something that is set up to prevent against future loss or mishap. |
interest | (n). Finance: money paid regularly at a particular rate for the use or loan of money. It can be paid by a finance organisation or bank to you (in the case of savings), or it may be payable by you to a finance organisation on money you borrowed from the organisation. See compound interest and simple interest, see also borrow. |
intermediate | (adj). A state in between. |
interquartile | (adj). Between quartiles. See quartile. |
interval | (n). Gap. A difference between two measurements. |
inverse | (n). The opposite of. Mathematics: one divided by. E.g. 1/2 is the inverse of 2. |
invest | (v). To put money into an organisation or bank (e.g. in buying shares) so as to gain interest on the amount at a higher rate. See interest. |
investment | (n). Something in which you have invested money (time, or effort, in common usage). |
investor | (n). A person who has invested (usually money). |
invoice | (n). A formal request for payment (in writing). It will usually state the name of the supplier or vendor (shop); the address of the shop or company that is requesting the amount; the VAT number of the shop; the words “Tax Invoice”; the shop’s invoice number; the date and time of the sale; a description of the items or services bought; the amount of VAT charged (14%); the total amount payable. |
K | |
kWh | (abbr). Unit of power (kilowatt hours) that electricity suppliers charge for. See power, watt. 1000 watts used in 1 hour = 1kWh = 1 unit. So e.g. a 2000 W heater uses 2 units per hour. |
L | |
liability | (n). To owe, or to have something that causes one to be in debt; something that causes you to have to spend money; a legal or financial responsibility. |
likely | (adj). To be probable; something that might well happen. |
linear | (adj). In a line. Mathematics: in a direct relationship, which, when graphed with Cartesian coordinates, turns out to be a straight line. |
logarithm | (n). Mathematics: a quantity representing the power by which a fixed number (the base) must be raised to produce a given number. The base of a common logarithm is 10, and that of a natural logarithm is the number e (2,7183…). A log graph can turn a geometric or exponential relationship, which is normally curved, into a straight line. |
longitude | (n). Lines running north to south on the earth, measuring how far east or west one is, in degrees, from Greenwich in the UK. “Longitudinal” (adj) means from north to south, or top to bottom. Running lengthwise. Physics: a wave whose vibrations move in the direction of propagation (travel). Example: sound. Statistics: a study in which information is gathered about the same people or phenomena over a long period of time. |
M | |
magnitude | (n). Size. |
manipulate | (v). To change, or rearrange something. Usually in Mathematics it means to rearrange a formula to solve for (to get) an answer. |
mean | (n). See average. |
mechanical | (n). By means of physical force. |
median | (n). Mathematics: the number in the middle of a range of numbers written out in a line or sequence. |
member | (n). A part of. Finance: a person or legal entity who is partial owner of a company. |
meter | (n). A device to measure something. You might see this spelling used in American books for metre. See metre. |
metre | (n). The SI unit of length, 100 cm. |
metric | (adj). A measurement system, using a base of 10 (i.e. all the units are divisible by 10). The USA uses something known as the Imperial system, which is not used in science. The Imperial system is based on 12. Examples:
|
minimise | (v). To make as small as possible. |
minimum | (n). The smallest amount possible. |
modal | (adj). Pertaining to the mode, or method. Can mean: about the mathematical mode or about the method used. See mode. |
mode | (n). Mathematics: the most common number in a series of numbers. See also mean, median. |
model | (n). A general or simplified way to describe an ideal situation, in science, a mathematical description that covers all cases of the type of thing being observed. A representation. |
N | |
numerator | (n). The opposite of a denominator; the number on top in a fraction. |
O | |
optimal | (adj). Best, most. |
origin | (n). Mathematics: the centre of a Cartesian coordinate system. General use: the source of anything, where it comes from. |
outlier | (n). Statistics: a data point which lies well outside the range of related or nearby data points. |
P | |
parallel | (adj). Keeping an equal distance along a length to another item (line, object, figure). Mathematics: two lines running alongside each other which always keep an equal distance between them. |
particular | (adj). A specific thing being pointed out or discussed; to single out or point out a member of a group. |
PAYE | (abbr). Pay as you earn, tax taken off your earnings by your employer and sent to the South African Revenue Service before you are paid. |
per | (prep). For every, in accordance with. |
per annum | (adv). Once per year; for each year. |
percent | (adv). For every part in 100. The rate per hundred. |
percentile | (n). A division of percentages into subsections, e.g. if the scale is divided into four, the fourth percentile is anything between 75 and 100%. |
perimeter | (n). The length of the outer edge; the outer edge of a shape. |
period | (n). The time gap between events; a section of time. |
periodic | (adj). Regular; happening regularly. |
perpendicular | (adj). At right angles to (90˚). |
pi | (n). π, the Greek letter p, the ratio of the circumference of a circle to its diameter. A constant without units, value approximately 3,14159. |
plan | (n). Architecture: a diagram representing the layout and structure of a building, specifically as viewed from above. More general use: any design or diagram, or any intended sequence of actions, intended to achieve a goal. |
plot | (v). To place points on a Cartesian coordinate system; to draw a graph. |
policy | (n). Finance: a term referring to an account held with an insurance company; an agreement that the company insures you. General use: a prescribed course of action. |
predict | (v). General use: to foresee. Mathematics: see extrapolation. |
premium | (n). An amount paid by you to an insurance company for your policy. See policy. General use: expensive or valuable. |
probability | (n). How likely something is. See likely. Probability is generally a mathematical measure given as a decimal, e.g. [0] means unlikely, but [1,0] means certain, and [0,5] means just as likely versus unlikely. [0,3] is unlikely, and [0,7] is quite likely. The most common way to express probability is as a frequency, or how often something comes up. E.g. an Ace is 1/13 or 0,077 likely, in a deck of cards, because there are 4 of them in a set of 52 cards. |
product | (n). Mathematics: the result of multiplying two numbers. |
project | (n. & v.). A project (n., pronounced PRODJ-ekt) is a plan of action or long-term activity intended to produce something or reach a goal. To project (v., pronounced prodj- EKT), is to throw something, or to guess or predict (a projection). To project a result means to predict a result. See extrapolate. |
proportion | (n). To relate to something else in a regular way, to be a part of something in relation to its volume, size, etc; to change as something else changes. See correlate and respectively. |
Pythagoras’s Theorem | (n). The square on the hypotenuse is equal to the sum of the squares on the other two sides of a right- angled triangle. Where h is the hypotenuse, a is the side adjacent to the right angle, and b is the other side: h2 = a2 + b2. |
Q | |
qualitative | (adj). Relating to the quality or properties of something. A qualitative analysis looks at changes in properties like colour, that can’t be put into numbers. Often contrasted with quantitative. |
quantitative | (adj). Relating to, or by comparison to, quantities. Often contrasted with qualitative. A quantitative analysis is one in which you compare numbers, values and measurements. |
quantity | (n). Amount; how much. |
quartile | (n). A quarter of a body of data represented as a percentage. This is the division of data into 4 equal parts of 25% each. To determine the quartiles, first divide the information into two equal parts to determine the median (Q2), then divide the first half into two equal parts, the median of the first half is the lower quartile (Q1), then divide the second half into two equal parts, and the median of the second half is the upper quartile (Q3). Data can be summarised using five values, called the five number summary, i.e. the minimum value, lower quartile, median, upper quartile, and maximum value. |
R | |
radius (sing), radii (plur) | (n). The distance between the centre of an object, usually a circle, and its circumference or outer edge. Plural is pronounced “ray-dee-eye.” |
random | (n). Unpredictable, having no cause or no known cause. Done without planning. |
range | (n). Mathematics: the set of values that can be supplied to a function. The set of possible y-values in a graph. See domain. |
rate | (n). How often per second (or per any other time period). Finance: the exchange rate or value of one currency when exchanged for another currency; how many units of one currency it takes to buy a unit of another currency. Also “interest rate”, or what percentage of a loan consists of interest charges or fees. |
ratio | (n). A fraction; how one number relates to another number; exact proportion. If there are five women for every four men, the ratio of women to men is 5:4, written with a colon (:). This ratio can be represented as the fraction 5/4 or 11/4 or 1,25; or we can say that there are 25% more women than men. |
rebate | (n. & v.). To send some money back to a person who has paid too much (v). An amount sent back to someone who has paid too much (n). |
receipt | (n). Finance: a piece of paper or other evidence sent to show that an amount was paid and that the person who received it (recipient) wishes to acknowledge (show) that they received (got) it. |
receive | (v). To get something. |
reception | (n). The process of receiving something. In common use, it can mean to greet people or “receive” them in your house. It can also refer to receiving (getting) a radio or microwave signal, e.g. in a cellphone or radio. |
refund | (n). To send back a full payment made by someone who has paid incorrectly. See rebate. |
remainder | (n). Leftovers. Mathematics: an amount left over after division which cannot be divided further unless one wishes to have a decimal or fraction as a result, i.e. where the divisor does not exactly divide the numerator by an integer (whole number). |
S | |
scale | (n). A system of measurement, with regular intervals or gaps between units (subdivisions) of the scale. |
sector | (n). General use: a subdivision. In Economics or Finance: a part of the economy that is responsible for a particular industry or performs a particular service. |
simple interest | (n). Interest charged on the original amount due only, resulting in the same fee every time. |
simplify | (v). To make simpler. Mathematics: to divide throughout by a common factor (number or algebraic letter) that will make the equation easier to read and calculate. |
solution | (n). Mathematics: the step-by-step displaying of calculations to arrive at answers. Common use: the answer to a problem, in the sense of dissolving (removing) a problem. |
solve | (v). To come up with a solution (answer). Show your working. |
square | (n). Mathematics: a shape or figure with four equal sides and only right angles; the exponent 2 (e.g. the square of 4 is 42 = 16). |
squared | (adj). Having been multiplied by itself, put to the exponent 2. See square. |
statement | (n). Finance: a summary of transactions (debits and credits, or payments and receipts) made on an account. See account, debit, credit. |
statistics | (n). The mathematics of chance and probability. |
subscript | (n). A number placed below the rest of the line, e.g. CO2. |
substitute | (v). To replace. |
substitution | (n). The process of substituting. Mathematics: to replace an algebraic symbol in a formula with a known value or another formula, so as to simplify the calculation. See simplify. |
subtotal | (n). Finance: the total amount due on a statement or invoice, usually without VAT (tax) charges given. Or: a total for a section of an invoice or statement or series of accounts, but not the total of the whole invoice, statement or account. |
sum | (n. & v.). To add things up. Represented by Greek Sigma (s): ∑ or the plus sign (+). |
superscript | (n). A number placed above the rest of the line, e.g. πr2. |
T | |
tally | (n). A total count; to count in fives by drawing four vertical lines then crossing through them with the fifth line. |
tangent | (n). Mathematics: a straight line touching a curve only at one point, indicating the slope of the curve at that point; the trigonometric function of the ratio of the opposite side of a triangle to the adjacent side of a triangle in a right-angled triangle; a curve that goes off the chart. |
tax | (n). A compulsory levy imposed on citizens’ earnings or purchases to fund the activities of government. |
taxable | (adj). A service, purchase or item or earning that has a tax applied to it. |
transaction | (n). Finance: Exchanging money (payment or receipt); a credit and a debit. |
transfer | (n). To move from one place to another. Finance: usually refers to a payment or credit. See credit, debit, transaction. |
trends | (n). Mathematics: regular patterns within data. |
trigonometry | (n). Mathematics: the relationship and ratios between sides and angles within a right-angled triangle. |
U | |
UIF | (abbr). Unemployment Insurance Fund. A government-run insurance fund which employers and employees contribute to, so that when employees are retrenched they can still collect some earnings. |
unit | (n). A subdivision of a scale. See scale. |
V | |
variable | (n. & adj.). A letter used to represent an unknown quantity in algebra (n); a quantity that changes (n); subject to change (adj). |
volume | (n). A measure of the space occupied by an object, equal to length x breadth x height. |
W | |
watt | (n). Unit of power or rate of use of energy. |
wattage | (n). The amount of power being used, usually rated in kWh. See kWh. |
withdraw | (v). To remove. Finance: to take money out of an account that belongs to you. Compare debit. |
Y | |
yard | (n). Old Imperial measurement of length, approximately equal to a metre (1,09 m). |
The maths you need
This section gives you the basic mathematical skills that you need to pass any subject that makes use of mathematics. Do not go any further in this book until you have mastered this section.
- If a formula does not have a multiplication (×) sign or a dot-product (·), and yet two symbols are next to each other, it means “times”. So, m1m2 means mass 1 times mass 2. You can also write it as m1 × m2, or m1·m2
- Comma means the same as decimal point on your calculator (i.e. 4,5 = 4,5). Do not confuse the decimal point with dot product (multiply): 4,5 = 4½ but 4·5 = 20. Rather avoid using the dot product for this reason.
- A variable is something that varies (means: changes). So, for example, the weather is a variable in deciding whether to go to the shops. Variables in science and mathematics are represented with letters, sometimes called algebraic variables. The most common you see in maths is x, probably followed by y, z.
2. Subject of Formula or Solving For
Very often in mathematics you have to “make something the subject of a formula” or “solve for something”. This refers to finding the value of an unknown quantity if you have been given other quantities and a formula that shows the relationship between them.
The word ‘formula’ means a rule for working something out. We work with formulas to draw graphs and also to calculate values such as area, perimeter and volume. You are usually given the formulas in an exam question, so you don’t have to remember them, but you do need to select the right numbers to put into the formula (substitute). For example, the formula for the area of a triangle is
Area = ½ base × height.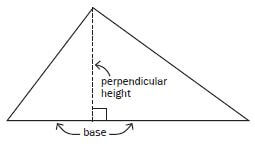
In this formula:
- the word Area stands for the size of the area of a triangle (the whole surface that the triangle covers)
- the word base stands for the length of the base of the triangle
- the word height stands for the length of the perpendicular height of the triangle.
A formula can be written in letters rather than words, for example:
A = ½ b × h.
The quantity on its own on the left is called the subject of the formula.
Worked example 1
If John has 5 apples, and he gives some to Joanna, and he has two apples left, how many did he give to Joanna? Well, the formula would be something like this:
5 – x = 2
To solve for x, we simply have to swap the x and the 2. What we’re actually doing is adding “x” to both sides:
5 – x + x = 2 + x
this becomes:
5 = 2 + x
then we subtract 2 from both sides to move the 2 over: 5 – 2 = 2 – 2 + x
5 – 2 = x
3 = x ... so John gave Joanna three apples.
The same procedures apply no matter how complex the formula looks. Just either add, subtract, square, square root, multiply or divide throughout to move the items around.
Worked example 2
Let’s take an example from Physical Science: V = IR. This means, the voltage in a circuit is equal to the current in the circuit times the resistance.
Suppose we know the voltage is 12 V, and the resistance is 3 Ω. What is the current?
V = IR
12 = 3 × I
divide throughout by 3 so as to isolate the I
12 = (12) × I
3 (3)
remember that anything divided by itself is 1, so :
12 = (1) × I ... and 12 = 4 ....so
3 3
4 = I or
I = 4A ....The circuit has a current of 4 amperes.
Worked Example 3
Here’s a more tricky example from Physical Science.
Given Kc = 4,5
[SO3] = 1,5 mol/dm3
[SO2] = 0,5 mol/dm3
[O2] = (x - 48) mol/dm3
64
Kc = [SO3]2 ∴4,5 = (1,5)2
[SO2]2[02] (0,5)2 (X - 48)/64
∴x = 176g
Step by Step
Let’s see how it works.
First, solve for the exponents (powers):
- 4,5 = 2,25
(0,25) (X - 48)/64
Now, we can see that 2,25 and 0,25 are similar numbers (multiples of five), so let’sNow, we can see that 2,25 and 0,25 are similar numbers (multiples of five), so let’s divide them as shown.
- 4,5 = 2,25 × (x - 48)
(0,25) 64
That leaves us withThat leaves us with
- 4,5 = 9 × (x - 48)
64
But if we’re dividing a divisor, that second divisor can come up to the top row. Here’s aBut if we’re dividing a divisor, that second divisor can come up to the top row. Here’s asimple example:
- 1 ÷ (2 ÷ 3) = 1/2/3
= 1 × 3
2
= 3/2 = 1,5
If you doubt this, try it quickly on your calculator: 1 ÷ (2 ÷ 3) ... this means, one, dividedIf you doubt this, try it quickly on your calculator: 1 ÷ (2 ÷ 3) ... this means, one, dividedby two-thirds. Well, two-thirds is 0,6667, which is almost one. So how many “twothirds”do you need to really make up one? The answer is one and a half “two-thirds”...i.e. 0,6667 + (0,6667 ÷ 2) = 1. Hence the answer is 1,5.
So, back to the original problem, we can bring the 64 up to the top line and multiply itby nine:
- 4,5 = 9 × (x - 48)
64
4,5 = 9 × 64
x -48
4,5 = 576
x - 48
Now we can inverse the entire equation to get the x onto the top:
- 1 = x - 48
4,5 576
Now we multiply both sides by 576 to remove the 576 from the bottom row
- 576 = (x – 48) 576 (note the 576 on the right cancel each other out)
4,5 576
and we cancel the 576’s on the right hand side as shown above. Now, if 576 ÷ 4,5 = 128, then
- 128 = x – 48
Now we add 48 to both sides to move the 48 across
- 128 + 48 = x – 48 + 48 ... hence, 128 + 48 = x = 176.
Worked example 4
A triangle has a base of 6 cm and a perpendicular height of 2 cm. Determine its area.
Step 1: Write down the value that you need to find. | Need to find: Area |
Step 2: Write down the information that you have. Write down the numbers and the units. | base = 6 cm height = 2 cm |
Step 3: Write down the formula that you are going to use. | Area = ½ base × height |
Step 4: Write down the formula again, but write the numbers that you know instead of the words or letters. | Area = ½ × 6 cm × 2 cm |
Step 5: Now calculate. | = 3 cm × 2 cm |
Step 6: Write your answer with the correct units. | = 6 cm2 |
Worked example 5
Calculate the area and the perimeter of the triangle alongside.
This looks like an easy problem, but you need to stay on your toes. As you follow the steps you will see why.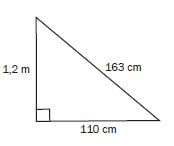
Step 1: Write down what you need to find. | Need to find: Area and Perimeter. Let’s start with area. |
Step 2: Write down the information that you have. | From the diagram:
The sides of the triangle are at right angles to each other, so one side is the perpendicular height. |
Step 3: Write down the formula. | Area = base = ½ × height |
Step 4: Write down the formula again, but write the numbers that you know instead of the words. | Area = ½ × 110 cm × 120 cm |
Step 5: Now calculate. | = 55 cm × 120 cm |
Step 6: Write your answer with the correct units. | = 6 600 cm2 |
Step 7: Calculate the perimeter. | Perimeter = 120 + 163 + 110 = 393 cm |
Worked example 6
In the United States, people use degrees Fahrenheit to measure temperature. Convert 67 °F into degrees Celsius (°C). Round off your answer to two decimal places.
The formula to use is °C = (°F – 32°) ÷ 1,8.
Need to find: Temperature in degree Celsius. | Notes |
Information we have: Temperature in degrees Fahrenheit = 67 °F. | |
°C = (67° – 32°) ÷ 1,8 | Replace °F with 67° in the formula: |
°C = 35° ÷ 1,8 | Remember the order of operations: Calculate the brackets first and then do the division. |
°C = 19,444 …° | Round off to two decimal places. |
Temperature in degrees Celsius = 19,44 °C | Look at the number in the third decimal place. It is less than 5, so round the second decimal place down. |
Worked example 7
A circular piece of land has a diameter of 40 m. What is the area of the land?
Use the formula: A = πr2 for the area of a circle and use the value of 3,142 for π.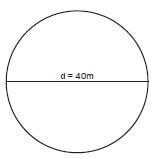
Need to find: Area | Notes | |
Information we have: diameter = 40 m; π = 3,142 | NB Always make sure you use the quantity that is written in the formula – radius, not diameter. | |
Butwe need the radius, which is half of the diameter, so r = 20 m. | ||
A = πr2 | ||
A = 3,142 × (20)2 | A = πr2 means Area = pi times the radius squared. | |
A = 3,142 × (20 × 20) A = 3,142 × 400 | ||
A = 1 256,8 m2 | Are the units right? Yes, the diameter was given in metres, so the area will be in square metres (m2 ). | |
Worked example 8
When we work with a formula, we want the quantity that we are calculating on its own on one side of the formula, so that it is the subject of the formula.
We can work out area easily if the formula is Area = length × breadth. Now let’s use the same formula to find the length.
Step 1 | Look at the formula. Which is the quantity that you want to calculate? | Area = length × breadth | ||
Step 2 | What do you need to do to get length on its own? | |||
Step 3 | Divide both sides by breadth: | Area ÷ breadth = length × breadth ÷ breadth | ||
Step 4 | Now simplify the formula: area ÷ breadth | = length (because: breadth ÷ breadth = 1) | ||
Step 5 | Length = | area ÷ breadth | ||
Step 6 | Use the formula to solve the problem by substituting the values for area and breadth. | |||
Worked example 9
To calculate the profit made from selling an item, we use the formula: profit = selling price – cost price.
But what if we already know the profit and the cost price, but we need to calculate the selling price?
An example: It costs R121 to buy a necklace at cost price, and Thabo wants to make R65 profit. How much must he sell it for? (What is the selling price?)
Selling price | ||
Step 1 | Look at the formula. Which is the quantity that you want to calculate? | profit = selling price – cost price |
Step 2 | Substitute the values thatyou have i.e. profit and cost price. | R65 = SP – R121 |
Step 3 | Add cost price to both sides. | R65 + R121 = SP – R121+ R121 |
Step 4 | Now simplify. | R186 = SP (because cost price – cost price = 0) |
Worked example 10
This example has a fraction in it. See what you need to do in that case to make a quantity the subject of the formula.
5 miles is approximately the same as 8 kilometres. The formula to convert kilometres to miles is:
- number of miles = 5 × number of kilometres.
8
Gavin has cycled 30 miles and he wants to know what this is in kilometres. The formula must start with “number of kilometres = … ”
Rearrange the formula. Then work out how many kilometres he has cycled.
Step 1 | Look at the formula. Which is the quantity that you want to calculate? | number of miles = 5/8 × number of kilometres |
Step 2 | Number of kilometres is multiplied by 5/8. So we need to multiply by 8/5 because 5/8 × 8/5 = 1. | |
Step 3 | Multiply both sides by 8/5. | number of miles × 8/5 = 5/8 × number of kilometres × 8/5 |
Step 4 | Now simplify the formula: | number of miles × 8/5 = 5/8 × 8/5 × number of kilometres |
Cancel out: 5/8 × 8/5 = 1. | number of miles × 8/5 = number of kilometres | |
Step 5 | Now we have number of kilometres = number of miles × _8 5 | |
Step 6 | Use the formula to solve the problem. | number of kilometres = number of miles × 8/5 |
Worked example 11
Thami needs to make a circle with an area of 40 cm2. What should the radius of the circle be? Round off your answer to two decimal places.
The formula for the area of a circle is A= πr 2. Use the value of 3,142 for π.
Step 1 | Look at the formula. Which is the quantity that you want to calculate? | A = πr 2 |
Step 2 | What do you need to do to get radius on its own on one side of the equation?
| |
Step 3 | Divide both sides by π | Area ÷ π = πr 2 ÷ π |
Step 4 | When then have | Area ÷ π = r 2 |
Now take the square root of both sides. | √Area =√r 2 | |
Step 5 | Now we have r = √Area | |
Step 6 | Use the formula to solve the problem, by substituting the given values. | r = √Area |
3. Statistics
You should know the following terminology:
- Dependent variable: The thing that comes out of an experiment, the effect; the results.
- Independent variable(s): The things that act as input to the experiment, the potential causes. Also called the controlled variable.
- Control variable: A variable that is held constant in order to discover the relationship between two other variables. “Control variable” must not be confused with “controlled variable”.
- Correlation does not mean causation. That is, if two variables seem to relate to each other (they seem to co-relate), it doesn’t mean that one causes the other. A variable only causes another variable if one of the variables is a function f(x) of the other. We will see more about this when we look at graphs, below.
- Mean: The average. In the series 1, 3, 5, 7, 9, the mean is 1 + 3 + 5 + 7 + 9 divided by 5, since there are 5 bits of data. The mean in this case is 5.
- Median: The datum (single bit of data) in the precise middle of a range of data. In the series 1, 3, 5, 7, 9, the median value is 5.
- Mode: The most common piece of data. In the series 1, 1, 2, 2, 3, 3, 3, 4, 5, the mode is 3.
4. Triangles
The area of a triangle is half the base times the height: a = b/2(h). A triangle with a base of 5 cm and a height of 3 cm will have an area of 2,5 × 3 = 7,5 cm2.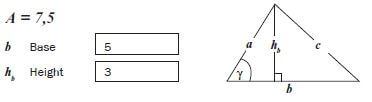
Lengths of Triangle Sides
You can calculate the lengths of sides of right-angled triangles using Pythagoras’ Theorem. The square of the hypotenuse is equal to the sum of the squares of the other two sides: In this diagram, b = base, hb = height, and c = the hypotenuse: c2 = hb2 + b2.
Worked example 12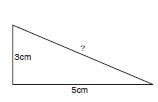
In the triangle shown, the hypotenuse, marked “?”, can be obtained by squaring both sides, adding them, and then square-rooting them for the length of the hypotenuse.
That is: 32 + 52 = 9 + 25 = 34. Since in this case 34 = hyp2 it follows that the square root of 34 gives the value of “?”, the hypotenuse. That is, 5,83cm.
5. Graphs
It’s probably best to start from scratch with Cartesian Coordinates.
“Coordinates” are numbers that refer to the distance of a point along a line, or on a surface, or in space, from a central point called the “origin”. Graphs that you will use have only two dimensions (directions). The positions of points on these graphs are described using two coordinates: how far across (left-to-right) the point is, called the x-coordinate, and how far up-or-down on the page the point is, called the y-coordinate.
Worked example 13
Consider the following graph. It shows six points in a straight line.
The coordinates shown can be described using what are called “ordered pairs”. For example, the furthest point in this graph is 3 units across on the “x-axis” or horizontal line. Likewise, it is also 3 units up on the y-axis, or vertical (up and down) line. So, its coordinates are (3;3). The point just below the midpoint or “origin”, is one unit down of the x-axis, and one unit left of the y-axis. So its coordinates are (–1;–1). Note that anything to the left or below of the origin (the circle in the middle), takes a minus sign.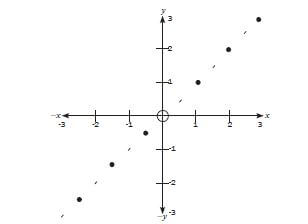
This series of dots look like they’re related to each other, because they’re falling on a straight line. If you see a result like this in an experimental situation, it usually means that you can predict what the next dot will be, namely, (4;4). This kind of prediction is called “extrapolation”. If you carry out the experiment, and find that the result is (4;4), and then (5;5), you’ve established that there is a strong relation or correlation.
Now, another way of saying that x relates to y, or x is proportional to y, is to say that y is a function of x. This is written y = f(x). So, in the example given above, voltage is a function of resistance. But how is y related to x in this graph? Well, it seems to be in a 1 to 1 ratio: y = x. So the formula for this graph is y = x. In this case, we’re only dealing with two factors; y = x and y.
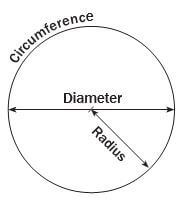
- Diameter is the width of a circle (2r); radius is half the diameter (d/2).
The edge of a circle is called the “circumference”. “Diameter” means to “measure across”. Compare “diagonal” which means an angle across a square or rectangle, so “dia-” means “across” (Greek). “Circumference” means to “carry in a circle” (Latin); think of how the earth carries us in a circle or orbit around the sun. To remember the difference between these things, just remember that the sun’s rays radiate out from the sun in every direction, so the radius is the distance from the centre of a circle, e.g. the sun, to the outer edge of a circle surrounding it, e.g. earth’s orbit (the circumference). - Area of a circle = π r2
- Circumference = 2 π r
- You can use the above to solve for radius or diameter
7.1 Reading Tables
A table is a way of showing information in rows and columns.
Getting information from tables
Reading a table means finding information in the cells. Each block in a table is called a cell. Reading a table is like reading a grid.
Look at the table on the below.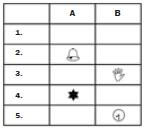
A and B are the column headings.
1, 2, 3, 4, and 5 are the row headings.
- What is in A2? Go across to column A and read down to row 2. A bell.
- What is in B3? A hand.
- Give the row and column for the star. Row 4 and column A. You can also write A4.
- Give the row and column for the clock. Row 5 and column B. You can also write B5.
Worked example 14
Look at the table below. In a question, you might have to find information in the table and write it down, or you might have to use the information in the table to do a calculation.
The table below shows the average maximum and minimum temperatures (highs and lows) in Mauritius (measured in degrees Celsius) each month.
Average monthly maximum and minimum temperatures in Mauritius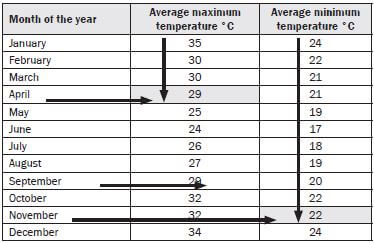
NB:
- This shows that in April the average maximum temperature was 29 °C.
- This shows that in November the average minimum temperature was 22 °C.
The table doesn’t have units in the cells, but we know the units because they are in the headings for each column.
Always give the units in your answer.
Look at the table above to answer these questions.
- Which month of the year had the highest average maximum temperature in Mauritius?
- Which month had the lowest average maximum temperature?
- What is the difference between theaverage maximum temperature in December and the average minimum temperature in December?
Solution
- Reading down the average maximum temperature column, you can see that January has a temperature of 35 °C, and none of the other temperatures are higher.
- The lowest maximum temperature is 24 °C in June.
- Here you will need to find the row for December and look across to get the lowest and highest temperatures for that month, then subtract the lowest temperature from the highest temperature to find the difference: 34 – 24 = 10°C.
Worked example 15
The average monthly increases in the cost of electricity (excluding VAT) between 2011 and 2012
Electricity consumption in kWh | ||||
50 | 150 | 600 | 1 000 | |
Amount payable in 2011 | R27,35 | R85,83 | R393,67 | R728,63 |
Amount payable in 2012 | R28,83 | R94,99 | R467,43 | R888,83 |
Increase between 2011 and 2012 | R1,48 | R9,16 | R73,67 | R160,20 |
Percentage increase between 2011 and 2012 | 5,39% | 10,67% | 18,74% | 21,99% |
Read from the table to answer the questions.
- If a household used 600 kWh of electricity in 2011, what would they have paid?
- How much more would you pay for 1 000 kWh of electricity in 2012 compared to 2011?
- What was the percentage increase for 150 kWh of electricity between 2011 and 2012?
- Was the percentage increase higher for lower electricity consumption, or for higher electricity consumption?
Solution
When you answer a question like this, take a few minutes to look at the table and write down some notes about what it shows. Don’t get too detailed, just to understand what the table is showing.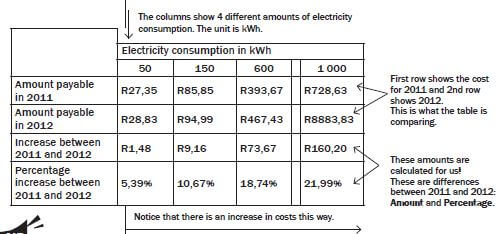
- Read off the 2011 row showing the amount, and the 600 kWh column: R393,67.
- You don’t have to calculate; this difference is given in the third row.
- The percentage increase is given in the last row. So look at the last row and second column (for 150 kWh): 10,67%.
- In the fourth row, there is a steady increase in the percentages from lower to higher electricity consumption. So the percentage increase is bigger for higher consumption.
7.2 Reading Two-Way Tables
Two-way tables are a useful way to display information, and they help you to work out missing information.
These tables show the numbers of two categories for the same sample.
One category is shown in rows, and the other category is shown in columns.
For example, the table below shows how many Grade 12 learners in a school own a cell phone or not and how many of the same learners own a music player or not.
Own an MP3 player | Do not own an MP3 player | |
Own a cell phone | 57 | 21 |
Do not own a cell phone | 13 | 9 |
What’s interesting about this table is that the totals of both columns and the totals of both rows are the same. We can see that the sample was of 100 learners.
Own an MP3 player | Do not own an MP3 player | Total | |
Own a cell phone | 57 | 21 | 78 |
Do not own a cell phone | 13 | 9 | 22 |
Total | 70 | 30 | 100 |
Worked example 16
During one month, 75 of the 180 babies born in a hospital were boys, and 40 of the babies weighed 4 kg or more. There were 26 baby boys who weighed 4 kg or more.
- Put this information in a two-way table and fill in the missing numbers.
- What percentage of girl babies weighed 4 kg or more?
Solution
- First draw up the grid and fill in the information given. (It doesn’t matter whether you put the weights or the gender in the columns or rows.)
When you’ve got the table in this form, you can find the missing information. Work back from the totals. For example, if 26 of the baby boys weighed 4 kg or more, then 75 – 26 = 49 of them weighed less than 4 kg.Boys
Girls
Total
Weighed less than 4 kg
Weighed 4 kg or more
26
0
40
Total
75
180
Boys
Girls
Total
Weighed less than 4 kg
49
91
140
Weighed 4 kg or more
26
14
40
Total
75
105
180
- There were 14 girl babies who weighed 4 kg or more, out of a total of 105 girl babies.
14 × 100% = 13,33%
100
Worked example 17
One hundred passengers on a bus trip were asked whether they wanted chicken or beef and whether they preferred rice or potato for their meals. Out of 30 passengers who liked rice, 20 liked chicken. There were 60 passengers who chose chicken.
- Put this information in a two-way table and fill in the missing numbers.
- How many meals with beef and potato should the bus company produce?
Solution
- Here is the information we are given:
Chicken
Beef
Total
Rice
20
Potato
Total
60
- Here is the rest of the information:
Chicken
Beef
Total
Rice
20
10
30
Potato
40
30
70
Total
60
40
100