ANALYTICAL GEOMETRY GRADE 12 NOTES - MATHEMATICS STUDY GUIDES
Share via Whatsapp Join our WhatsApp Group Join our Telegram Group- Revise: Analytical Geometry
- The equation of a line
- The inclination of a line
- Circles in analytical geometry
Analytical geometry works with the Cartesian plane and with algebra to define points, lines and shapes.
9.1 Revise: Analytical Geometry
This topic is also called Coordinate Geometry
Gradient of a line
The gradient is the slope of a straight line. It shows how steep the line is.
The steeper the gradient, the bigger the angle it makes with the ground or the positive side of the x-axis.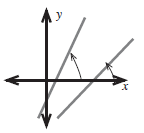
gradient m = y2 - y1
x2 − x1
OR
change in y
change in x
where (x1; y1) and (x2; y2) are two points on the line.
Parallel lines have equal gradients. AB ∥ CD and mAB = mCD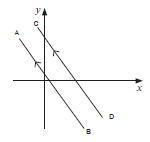
The product of the gradients of lines that are perpendicular is –1.
This means that the gradient of one line is the negative reciprocal of the gradient of the second line:
AB ⊥ PQ
mAB × mPQ = − 1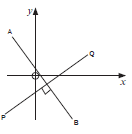
Note: The equation must always be in form y = mx + c
e.g.1
- The graphs of y = 2x + 1 and y = 2x + 5 are parallel because they both have m = 2.
The graphs of y = 2x + 1 and y = − ½ x + 5 are perpendicular
because 2x − ½ = − 1 - The distance formula
Learn the formula for distance:
Length of AB = √(x2 − x1)2 + (y2 − y1)2
You can also find the coordinates for a point on the line using the distance formula.
e.g.2
- L(-5;-2) and M (-1;-6) are two sets of co-ordinates on the same straight line. Determine the length of LM
LM = √(x2 − x1)2 + (y2 − y1)2
LM = √(− 5 + 1)2 + (− 2 + 6)2
= √16 + 16
= √32
= 4√2 - The length of the straight line PQ is given as 2 √5 . The co-ordinates of P (5;2) and Q(3;t) are given. Find the value(s) of t.
PQ = √(x2 − x1)2 + (y2 − y1)2
2√5 = √(5 − 3)2 + (2 − t)2
√20 = √4 + (4 − 4t + t2) square both sides
20 = 8 − 4t + t2
t2 − 4t − 12 = 0
(t − 6)(t + 2) = 0
t = 6 or t = −2
Activity 1
- For a line passing through the two points A(6; 6) and B(3; 2), calculate the length of AB. (3)
- If PQ = 5 units; P (5; t) and Q (1; –3) determine the possible value(s) of t. (3)
[6]
Solutions
|
3. The midpoint of a line
If you know the coordinates of the two endpoints of a line, you can find the point that is halfway between them. This is called the midpoint.
The midpoint of a line has the coordinates
( x1 + x2;y1 + y2)
2 2
where (x1; y1) and (x2; y2) are the endpoints of the line.
e.g.3
For a line passing through the two points A(6; 6) and B(3; 2), find the
coordinates of the midpoint of AB.
Midpoint of AB = ( x1 + x2;y1 + y2)
2 2
= (6 + 3 ; 6 + 2) = (4½ ;4)
2 2
So the midpoint has the coordinates (4½ ;4)
e.g.4
The coordinates of the midpoint of the line AB are (1;-4). Find the coordinates of A if the coordinates of B are (4;-3).
When midpoint is given:
x as the midpoint of AB = xA + xB and y as midpoint of AB = yA + yB
2 2
1 = xA + 4 and –4 = yA − 3
2 2
2 = xA + 4 and –8 = yA − 3
–2 = xA and –5 = yA
Coordinates of A are (-2;-5)
Activity 2
K (–1; –6) and L (5; 4) are two coordinates on the same straight line. Determine the coordinates of the midpoint. (2)
If M (–1; 4) is the midpoint of line segment AB, and the coordinates of A (3;6) are given, find the coordinates of the endpoint B. (3)
[5]
Solutions
We can use coordinate geometry to identify the properties of geometric |
Activity 3
A. (–4; 7), B (4; 5), C (0; –1) and D (a; b) are the vertices of parallelogram ABCD.
- Draw the parallelogram on squared paper. (2)
- Find the midpoint of the diagonal AC. (2)
- Use the information that you have to find the coordinates of point D. (3)
[7]
Solutions
|
9.2 The equation of a line
You can find the equation of a straight line using y = mx + c, if you know the gradient m and the y-intercept c.
You can also find the equation of a straight line using y − y1 = m (x − x1), if you know the gradient m and any point (x1; y1) on the line, or if two points given.
NOTE: y1 and x1 are the coordinates of a specific point on the line.
e.g.5
If the gradient of a line is –2 and the line cuts the y-axis at 1, then the equation of the line is y = –2x + 1.
e.g.6
If the gradient of a line is –2 and the point (4; –1) lies on the line, find the equation of the line.y − y1 = m (x − x1)
y – (–1) = –2(x – 4) substitute (4; –1) into the equation
y + 1 = –2x + 8 simplify
y = –2x +7 We usually put the answer in the form y = mx + c.
Summary
| If you know The gradient and the y-intercept The gradient and the coordinates of at least one point on the graph. Two points on the line: first calculate the gradient and then substitute into y = mx + c. | Formulae to use y = mx + c y − y1 = m (x − x1) or y = mx + c m = y2 −y1 and y = mx + c x2 - x1 |
Activity 4
- Determine the equation of the straight line that passes through the points P(1; 2) and Q(3; 8) in the form y = .... (3)
- Line AB is perpendicular to CD, which has a gradient of –2. The point (3; 4) lies on AB. Determine the equation of line AB. (2)
[5]
Solutions
|
9.3 The inclination of a line
In trigonometry, you used the ratios tan θ, sin θ and cosθ.
To find the inclination of a line, or the angle it makes with the x-axis, we use tan θ.
In triangle ABC, tan θ = opp = BA.
adj AC
BA is also change in y which is the gradient of AB.
AC change in x
We write gradient of AB as mAB.
So we can say mAB = tan θ
Angle θ shows the slope or inclination of the line AB.
θ is called the angle of inclination.
NOTE: θ ∈ (00;1800)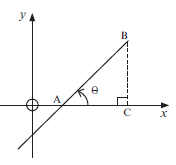
e.g.7
If tan θ = ½ , then θ = 26,56505 …° (Press: shift tan ½ on your calculator)
θ = 26,57 (rounded off to two decimal places)
Activity 5
Give your answers correct to two decimal places.
- Line AB is perpendicular to CD, which has a gradient of –4.
Find the inclination θ of AB. (2) - Determine the inclination of the straight line that passes through the points
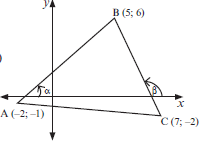
P (–6; 2) and Q (3; 10). (2) - Given the points A (–2; –1), B (5; 6) and C (7; –2), calculate the size of ABC . (6)
[10]
Solutions
|
Activity 6
- For a line passing through the two points A(6; 6) and B(3; 2):
1.1 Calculate the length of AB.
1.2 Find the coordinates of the midpoint of AB.
1.3 Calculate the angle of inclination of the line.
1.4 Determine the equation of the line passing through A and B.
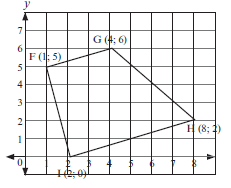
1.5 Determine the equation of a line GH perpendicular to AB passing through the midpoint of AB. (11) - F, G, H and I are the vertices of a quadrilateral shown below.
What kind of quadrilateral is FGHI? (5)
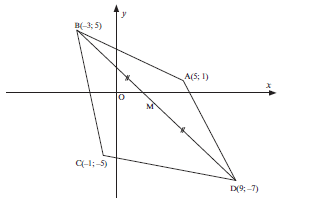
- ABCD is a quadrilateral with vertices A(5 ; 1), B(−3 ; 5), C(−1 ; −5) and D(9 ; −7).

3.1 Calculate the gradient of AC. (2)
3.2 Determine the equation of AC in the form y = … (3)
3.3 Hence, or otherwise, show that the midpoint M of BD lies on AC. (3)
3.4 Show that AMB = 90°. (2)
3.5 Calculate the area of ∆ ABC. (5)
[31]
Solutions
|
9.4 Circles in analytical geometry
A circle is made up of a set of points that are equidistant from its centre.
The circumference is the distance around the whole circle.
The distance from the centre to any point on the circumference of the circle is called the radius of the circle.
9.4.1 The equation of a circle
CIRCLE WITH CENTRE AT THE ORIGIN
We can use the distance formula to work out the equation of a circle with centre (0; 0).
If P(x; y) is any point on the circle with radius r, then
r = √(x − 0)2 + (y − 0)2
r2 = x2 + y2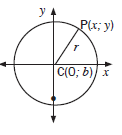
e.g.8
Find the equation of a circle centre 0 with the point P(5; 2) on its circumference.
x2 + y2 = r2 This is the general equation. We just need a value for r2.
(5)2 + (2)2 = r2 At the point (5; 2)
r2 = 25 + 4 = 29
∴ x2 + y2 = 29
CIRCLES NOT CENTRED AT THE ORIGIN
If we move the centre of the circle to any point
on the Cartesian plane C(a; b),
then (x – a)2 + (y – b)2 = r2
and r = √(x − a)2 + (y − b)2
Note: Recap on completing of the square on unit 2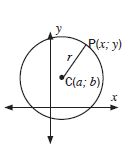
e.g.9
The equation of a circle is (x + 1)2 + (y – 3)2 = 16.
Determine the coordinates of the centre and the length of the radius.
The equation is already in the form (x – a)2 + (y – b)2 = r2, with a = –1, b = 3 and r2 = 16
So the centre is (–1; 3) and the radius is √16 = 4.
Remember that the radius can only be a positive number because it is a length.
Activity 7
- Determine the coordinates of the centre and the length of the radius if a circle has the equation: x2– 2x + y2+ 10y = –14 (3)
- Determine the equation of a circle with centre C(–1; –2) and passing through the point B(1; –6). (3)
[6]
Solutions
|
9.4.2 The equation of a tangent to a circle
A tangent is a straight line which touches a circle at one point only.
So ADB is a tangent, but AP is not a tangent.
A tangent to a circle at any point on the circumference is perpendicular to the radius at that point. So AB ⊥ CD.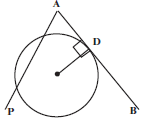
We can use all the formulae we know from analytical geometry to solve problems involving a tangent to a circle (distance, midpoint, gradient, angle of inclination, the equation of a line and the equation of a circle).
e.g.10
Find the equation of the tangent APB which touches a circle centre C with equation (x – 3)2 + (y + 1)2= 20 at P(5; 3).
| Solution Draw a sketch to help you. Centre of circle is C(3; –1) so the gradient of the radius CP (mCP) is 3 − ( −1) = 2. 5 - 3 radius ⊥ tangent, so mAPB × mCP = –1 and so mAPB = -½ Equation of tangent: y – y1 = m(x – x1) 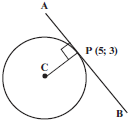 y – 3= -½ (x – 5) P is a point on the tangent y – 3= -½ x + 2½ y = -½ x + 5½ |
Activity 8
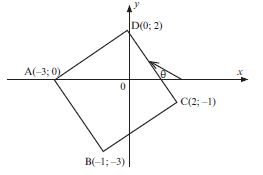
- ABCD is a quadrilateral with vertices A(–3; 0), B(–1; –3), C(2; –1) and D(0; 2).

1.1 Determine the coordinates of M, the midpoint of AC. (2)
1.2 Show that AC and BD bisect each other. (3)
1.3 Prove that A| D^ C = 90°. (4)
1.4 Show that ABCD is a square. (4)
1.5 Determine the size of θ, the angle of inclination of DC, correct to ONE decimal place. (3)
1.6 Does C lie inside or outside the circle with centre (0; 0) and radius 2? Justify your answer. (2)
[18]
| Solutions 1.1 Midpoint M of AC: 2 − 3; − 1 + 0 = ( − ½ ; -½) (2) 2 2 1.2 Midpoint M of BD: ( −1 + 0; − 3 + 2) = ( −½;-½) 2 2 ∴ So the midpoint of AC and the midpoint of BD are the same point, so they bisect each other.(3) 1.3 mAD= 2 − 0 = 2 and mDC= − 1 − 2 = −3 0-(0-3) 3 2-0 2 mAD × mDC = 2 × −3 = –1 3 2 1 ∴AD ⊥ DC ∴ADC = 90° (4) 1.4Here is one possible answer: The diagonals AC and BD bisect each other (proved in 1.2) ADC = 90° (proved in 1.3) AD2 = (2 – 0)2 + (0 – (–3))2 = 4 + 9 = 13
CD2 = (– 1 – 2)2 + (2 – 0)2 = 9 + 4 = 13 CD = √13 So adjacent sides are equal in length ∴ ABCD is a square. (4) 1.5 tan θ = mDC = − 1 − 2 = −3 2 - 0 2 θ = –56,3099324... + 180° θ = 123,7° (3) 1.6 OC2 = (2 – 0)2 + (– 1 – 0)2 OC2= 4 + 1 = 5 OC = √5 This is longer than the radius of 2 of the given circle, so C(2; –1) lies outside the circle 3. (2) [18] |
2. O is the centre of the circle in the figure below. P(x; y) and Q(12; 5) are two points on the circle. POQ is a straight line. The point R(t; –1) lies on the tangent to the circle at Q.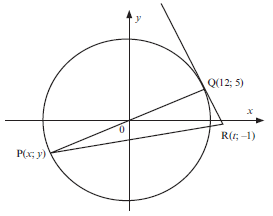
2.1 Determine the equation of the circle. (3)
2.2 Determine the equation of the straight line through P and Q. (2)
2.3 Determine x and y, the coordinates of P. (4)
2.4 Show that the gradient of QR is -12/5 (2)
2.5 Determine the equation of the tangent QR in the form y = … (3)
2.6 Calculate the value of t. (2)
2.7 Determine an equation of the circle with centre Q(12; 5) and passing through the origin. (3)
[19]
| Solutions The centre is at the origin, so x2 + y2 = r2. 2.1 OQ2 = (5)2 + (12)2 = 25 + 144 = 169 So the equation of the circle is x2 + y2 = 169 (3) 2.2 mPQ = mOQ = 0 – 5 = 5 0 - 12 12 PQ has y-intercept of 0. 3 (2) y = 5/12 x 2.3 By symmetry, P is the point (–12; –5). OR Substitute y = 5/12 x into x2 + y2 = 169 x2 + (5/12 x )2 = 169 x2 + 25/144 x2 = 169 144x2 + 25x2 = 169 × 144 169x2 = 24 336 x2 = 144 x = 12 or x = –12 x = –12 according to given diagram y = 5/12 x = 5/12 × (–12) = –5 (4) So P is the point (–12; –5). 2.4 tangent ⊥ radius so QR ⊥ PQ mPQ = 0 − 5 = 5 0 -12 12 ∴mQR = − 12/5 (2) 2.5 y = − 12/5 x + c OR y – y1 = − 12/5 (x – x1) Substitute Q(12; 5) into equation to find c: 5 = − 12/5 (12) + c y – 5 = − 12/5 (x – 12) 5 + 144/5 = c y =− 12/5 x + 144 + 5 c = 169/5 y = − 12/5 x + 169/5 y = − 12/5 x + 169/5(3) 2.6 R(t; –1) lies on line with equation y = − 12/5 x + 169/5 ∴ –1 = − 12/5 t + 169/5 –5 = –12t + 169 12t = 174 t = 14,5 (2) 2.7 OQ2 = (x – 12)2 + (y – 5)2 Q(12; 5) is centre of circle Substitute (0; 0) into equation: OQ2 = (0 – 12)2 + (0 – 5)2 OQ2 = 144 + 25 = 169 ∴ (x – 12)2 + (y – 5)2 = 169 (3) [19] |
What you need to be able to do:
From Grade 10 and 11:
- Find the distance between any two points on the Cartesian plane using the distance formula:
- Distance = √( x2 − x1 )2 + ( y2 − y1)2
- Find the midpoint between two points on a line, using the formula (x1 + x2, y1 + y2)
2 2
Find the gradient of line using m = y2 − y1
x2 - x1 - Find the equation of a line given:
- The gradient and the y-intercept using y = mx + c
- The gradient and the coordinates of at least one point on the graph.
- You can use y – y1 = m(x – x1)
- Two points on the line: first calculate the gradient, then substitute one of the points into y = mx + c.
- Find the inclination θ of a line, where m = tan θ.
- Find other angles, using geometry.
From Grade 12:
- Determine the equation of a circle with radius r and centre (a; b).
- Determine the equation of a tangent to a circle centre (a; b)
- Know the properties of triangles (isosceles, scalene, equilateral, right- angled triangle);square, rectangle, trapezium, rhombus and
parallelogram.
 (2)
(2)