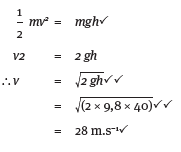Questions

Question 1: Multiple choice
Choose the correct answer. Only write the letter of the answer you select.
1.1 When vectors X and Y are added, the resultant R is incorrectly represented in dia- gram: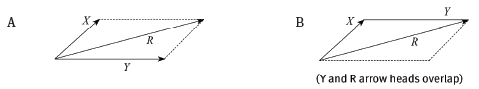

(3)

1.2 An athlete completed one lap of a 400 m oval track in 60 s. The magnitude of her average velocity for the race was:

1. 6,67 m.s^–1.
2. 15 m.s^–1.
3. 0 m.s^–1.
4. 4,8 m.s^–1. (3)

1.3 A car starts from rest and travels in a straight line for 10 s with a uniform acceleration of 2 m.s^–2. From the end of one second to the end of the next second, the car goes:

1. 2 m further than in the previous second.
2. 3 m further than in the previous second.
3. 6 m further than in the previous second.
4. 9 m further than in the previous second. (3)

1.4 A trolley moves to the right with increasing velocity and uniform acceleration. The ticker tape that it pulls through a ticker timer looks like this:
(3)
1.5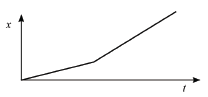

The velocity–time graph that corresponds with the above position–time graph is: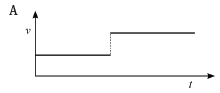

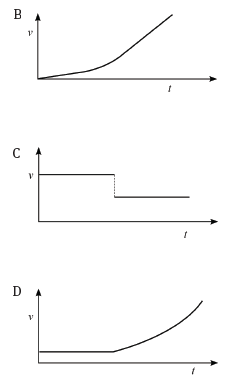(3)

1.6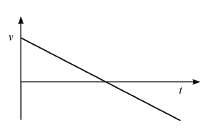

The position–time graph that matches the above velocity–time graph is: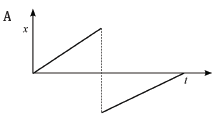

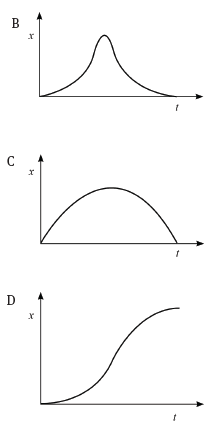 (3)

1.7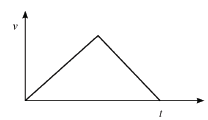

The acceleration–time graph that corresponds with the above velocity–time graph is: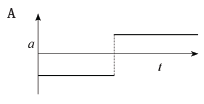 

(3)

1.8 When a car’s speed doubles:

1. the stopping distance is about twice as long.
2. the thinking distance is about four times as long.
3. the braking distance is about four times as long.
4. the stopping distance is about four times as long.

1.9 An object with potential energy EP is a height h above the Earth’s surface. It is then raised to a height 2 h. The new potential energy is:

1. 3 E_P.
   2
2. 2 EP.
3. 3 EP.
4. 4 EP. (3)

1.10 A stone falls through the air from a high bridge. As it falls: 

1. mechanical energy is conserved.
2. kinetic energy is conserved.
3. potential energy is conserved.
4. potential energy is transferred to kinetic energy and heat. (3)

Question 2: True/false
Indicate whether the following statements are true or false. If the statement is false, write down the correct statement.
2.1 Two force vectors, drawn to scale, are equal if they have the same length. (2)
2.2 Distance is change in position; it is a straight-line from the original position to the final position. (2)
2.3 Change in velocity is indicated by the area under a position–time graph. (2)
2.4 Acceleration is change in velocity. (2)
2.5 When a moving object doubles its speed, its kinetic energy also doubles. (2)

Question 3: One-word answers
Provide one word or term for each of the following descriptions. Write only the word or term next to the question number.
3.1 A physical quantity that has magnitude but not direction. (1)
3.2 The rate of change of displacement. (1)
3.3 Velocity at a particular time. (1)
3.4 Area under a velocity–time graph. (1)
3.5 When an object falls in the absence of air resistance, mechanical energy is … (1)

Question 4: Matching pairs
Choose an item from column B that matches the description in column A. Write only the letter of your choice (A–J) next to the question number.

[10]

Question 5: Long questions
Consider the physical quantities mass, weight, distance, displacement, speed, velocity, acceleration and energy.
5.1 Give the name and the abbreviation of the unit (or units) in which each is meas- ured. (6)
5.2 List those that are vector quantities and those that are scalar quantities. (4)
5.3 Using a scale of 10 mm to represent 10 m, draw vectors to represent:
5.3.1 a displacement of 50 m north. (2)
5.3.2 a displacement of 80 m east. (2)
5.4 Find the resultant of the two displacements in question 5 3 graphically:
5.4.1 by the tail-to-head method. (4)
5.4.2 by the tail-to-tail method. (3)
5.5 Check your answers to question 5.4 by calculating the resultant. Supply a rough sketch that helps to explain your calculation. (9) [30]

Question 6: Long questions
6.1 A golf ball falls vertically from the roof of a 12 m high building. It bounces upwards to a height of 9 m above the ground. Take the upward direction as the positive direction. What is the ball’s displacement, (1) when it strikes the ground; (2i) at the highest point of the bounce:
6.1.1 relative to the ground. (2)
6.1.2 relative to the top of the building. (2)
6.2 A cyclist rides halfway around a circular track with a radius of 140 m. She starts facing north and rides clockwise around the track. What is:
6.2.1 the distance that she rides? (3)
6.2.2 her displacement? (2)          [9]

Question 7: Long questions
7.1 A 707 km road journey from Durban to Johannesburg took 7 hours. Calculate the average speed for the trip:
7.1.1 in km.h^–1. (4)
7.1.2 in m.s^–1. (3)
7.2 If the displacement from the starting point in Durban to the ending point in Johannesburg was 644 km, calculate the magnitude of the average velocity for the trip (in km.h^–1). (4)
7.3 A skier, first moving at 8 m.s^–1 in a straight line on level snow, accelerates down a slope. After 10 s on the slope, she reaches a velocity of 20 m.s^–1. Calculate her average acceleration. (6)           [17]

Question 8: Long questions
A train transporting iron-ore from Sishen to Saldahna Bay travels on a straight track at 40 km.h^–1 for 4 hours. For this part of the trip, plot:
8.1 a position–time graph. (5)
8.2 a velocity–time graph. (5)
8.3 A ski-jumper starts from rest and moves down the first part of a straight track with constant acceleration. Taking the direction of motion as the positive direction, show in sketch graphs:
8.3.1 the shape of the position–time graph. (3)
8.3.2 the shape of the velocity–time graph. (3)
8.3.3 the shape of the acceleration–time graph. (3) [19]

Question 9: Long questions
The velocity–time graph of an object is shown below.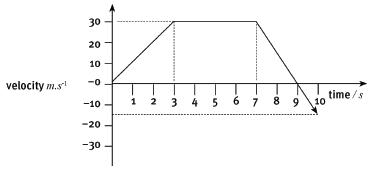

9.1 Describe the motion:
9.1.1 during the first 3 s. (3)
9.1.2 from t = 3 s until t = 7 s. (2)
9.1.3 from t = 7 s until t = 9 s. (3)
9.1.4 from t = 9 s until t = 10 s. (2)
9.2 Use the graph to find:
9.2.1 the uniform acceleration during the first 3 s of the motion. (5)
9.2.2 the uniform acceleration during the last 3 s of the motion. (4)
9.2.3 the displacement during the first 3 s of the motion. (5)
9.2.4 the displacement of the body while it moved with constant velocity. (3)
9.2.5 the displacement during the last 3 s of the motion. (5)
9.2.6 the total displacement for the full trip. (2)
9.2.7 the average velocity for the full trip. (5) [39]

Question 10: Long questions
The equations of uniform motion make use of the following symbols:
∆x, ∆t, vi , vf and a.
10.1 What quantity does each symbol represent? (5)
10.2 Name the abbreviated SI unit(s) in which each quantity is measured. (4)
10.3 An object moves horizontally in a straight line from rest with a constant acceleration of 2 m.s^–2. Complete the table below by replacing the question numbers with the correct values. (Note: You should only find it necessary to calculate in one of the rows.)

[23]

Question 11: Long questions
11.1 A motor cyclist travels at 18 m.s^–1 along a straight road. He accelerates uniformly for 6 s to a velocity of 30 m.s^–1. Calculate:
11.1.1 the acceleration of the motor cycle. (6)
11.1.2 the displacement of the motor cycle while accelerating. (6)
11.2 A car moving at 12 m.s^–1 along a straight road accelerates at 2 m.s^–2 for 5 s. Calculate:
11.2.1 the car’s displacement after 5 s. (6)
11.2.2 the car’s velocity after 5 s. (6)
11.3 A car moving with a velocity of 15 m.s^–1 is brought to rest over a distance of 37,5 m when the brakes are applied. Calculate the magnitude of the acceleration. (6)
11.4 A bullet leaves the barrel of a rifle at 1000 m.s^–1. If the barrel is 1 m long, calculate the magnitude of the acceleration of the bullet. Assume that the acceleration of the bullet is constant. (5)
11.5 A car travelling at 20 m.s^–1 has its brakes applied and slows down at a constant rate of 10 m.s^–2. What is the stopping distance of the car? (5) [40]

Question 12: Long questions
12.1 A man with a mass of 75 kg climbs a ladder to the flat roof of his house. If the vertical height of the roof is 3 m above the ground, how much gravitational potential energy has he gained? (5)
12.2 What is the gravitational potential energy of an object of mass 40 kg that is at a height of 30 m above the ground? (5)
12.3 Calculate the kinetic energy of a 72 kg parachutist, falling with a speed of 30 m.s^–1. (4)
12.4 An aircraft of mass 4000 kg flies with a speed of 150 m.s^–1 and maintains an altitude of 5000 m. Calculate its mechanical energy relative to the Earth’s surface. (7)
12.5 An object of mass 500 kg is raised to a height of 40 m. If the object falls freely from this height, what will its velocity be just before it strikes the ground? (6)
[27]

Answers

1.1 C 
1.2 A 
1.3 B 
1.4 A 
1.5 A 
1.6 C 
1.7 C 
1.8 C
1.9 B 
1.10 D 

2.1 Two force vectors, drawn to scale, are equal if they have the same length and direction. 
2.2 Displacement is change in position; it is a straight-line from the original position to the final position. 
2.3 Change in position is indicated by the area under a velocity–time graph. 
2.4 Acceleration is the rate of change in velocity. 
2.5 When a moving object doubles its speed, its kinetic energy becomes four times greater. 

3.1 scalar 
3.2 velocity 
3.3 instantaneous velocity 
3.4 displacement 
3.5 conserved 

4.1 J
4.2 E 
4.3 I 
4.4 H 
4.5 A 
4.6 B 
4.7 M 
4.8 G 
4.9 C 
4.10 D 

Question 5: Long questions
5.1

• mass: kilogram (kg) 
• weight: newton (N) 
• distance and displacement: metre (m) 
• speed and velocity: metre per second (m.s^–1) ?
• acceleration: metre per second squared (m.s^–2) ?
• energy: joule (J) ?

5.2 vectors: weight, displacement, velocity, acceleration ??
scalars: mass, distance, speed, energy ??
5.3.1 & 5.3.2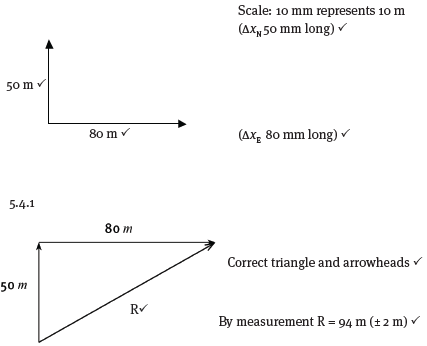

In the direction 58º (± 1º) east of north ?
5.4.2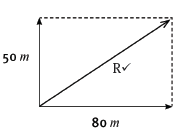

Correct rectangle and arrowheads ?
By measurement R = 94 m (± 2 m)
In the direction 58º (± 1º) east of north ?
5.5 By Pythagoras:
labelled sketch diagram ??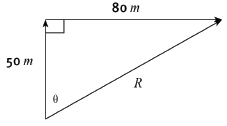

R² = 80² + 50²
∴R = √8900
= 94,34m

tan θ = 80
            50
∴θ =58º
By calculation, the resultant R = 94,34 m in the direction 58º east of north ?

Question 6: Long questions
6.1.1

• (1) 0 ?
  (2) +9 m ?

6.1.2

• (1) –12 m ?
  (2) –3 m ?

6.2.1

• Circumference of circle = 2∏r
  Half circumference of circle = ∏r? =2∆r 22 × 140 = 440m
                                                                   7
  Distance = 440 m ?

6.2.2

• Displacement = 140 m ? east ? 

Question 7: Long questions
7.1.1

• average speed = D ?= 707 ??=101 km.h^–1?
                              ∆t        7

7.1.2

• 101 km = 101000 m ??= 28,06 m.s^–1?
          h         3600 s

7.2

• magnitude of average velocity
  = ∆x = 644 ?= ??= 92 km.h–1? 
     ∆t       7

7.3 Average acceleration

• = ∆v = vf − vi = ? = (20^–8) ???= 1,2 m.s^–2 ?
     ∆t        ∆t                10
  The acceleration has a magnitude of 1,2 m.s^–2 and is in the same direction as the skier’s motion.?

Question 8: Long questions
8.1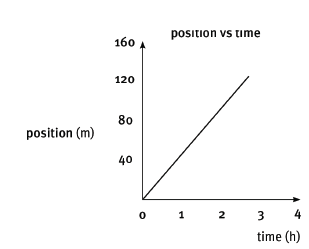

axes ? values on axes ??
shape of graph ??
8.2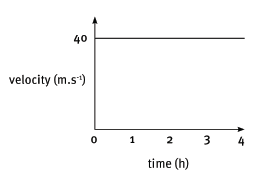

axes ? values on axes ??
shape of graph ??
8.3.1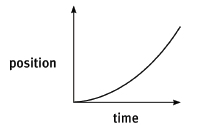

axes ?
shape of graph ??
8.3.2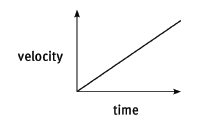

axes ?
shape of graph ??
8.3.3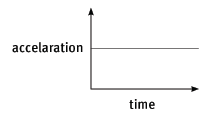

axes ?
shape of graph ??

Question 9: Long questions
9.1.1 Uniform acceleration ? from rest to 30 m.s^–1 ? in the positive direction ?
9.1.2 Constant velocity ? of 30 m.s^–1 in the positive direction ?
9.1.3 Uniform negative acceleration ? from 30 m.s^–1 in the positive direction to rest ?
9.1.4 Uniform negative acceleration ? from rest to 15 m.s^–1 ? in the negative direction ?
9.2.1 acceleration = gradient

• = (30 − 0) ??= 10 m.s^–2 ?
      (3 − 0)
  in the direction of motion ?

9.2.2 acceleration = gradient ?

• = ∆x
    ∆y
  = (−15 − 30) ??= –45 − 15 m.s^–2 ?
        (10 − 7)             3

9.2.3 displacement = triangular area under graph = ½ bh ?
= ½ × 3 ? × 30 ?
= 45 m ? in the direction of motion ?

9.2.4 displacement = rectangular area under graph = l × b
= 4 ? × 30 ?
= 120 m ? in the direction of motion

9.2.5 displacement = sum of two triangular areas under graph (area = ½ bh)
= (½ × 2 ? × 30 ?) + [½ × 1 ? × (–10) ?]
= 30 – 5
= 25 m ? in the direction of motion

9.2.6 total displacement = total area under graph
= 45 + 120 + 25 ?
= 190 m ? in the direction of motion

9.2.7 average velocity = ∆x ?= 190 ??= 17,27 m.s^–2 ?in the direction of motion ?
                                       ∆y        11

Question 10: Long questions
10.1

• ∆x displacement (change in position)?
• ∆t change in time ?
• vi initial velocity ?
• vf final velocity ?
• a uniform acceleration ?

10.2

• Dx m ?
• ∆t s ?
• vi and vf m.s^–1 ?
• a m.s^–2 ?

10.3

10.3.6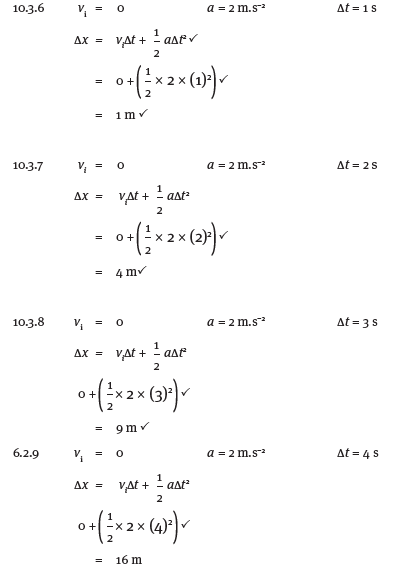

Question 11. Long questions
11.1.1 vi = 18 m.s^–1 vf = 30 m.s^–1 00100 ∆t = 6 s
Average acceleration = ∆v = vf − vi ?= (30 − 18) ???= 2 m.s^–2 ?
                                     ∆t         ∆t               6
in the direction of motion. ?
11.1.2

• ∆x = (vf + vi) ∆t?
               2
  = (18? + 30 ?) 6
            2
  = 144 m in the direction of motion?

11.2.1= 85 m in the direction of motion?
11.2.2 vf = v1 + a∆t ?
= 12? + (2 × 5)??
= 22 m.s^–1 in the direction of motion?
11.3 ∴ a = −3 m.s^–2 ?
The magnitude of the acceleration is 3 m.s^–2, ?and the acceleration is negative.
11.4 ∴ a = 5 × 10⁵ m.s ^–2 ?
11.5 ∴ ∆x = 20 m

Question 12: Long questions
12.1

• m = 75 kg g = 9,8 m.s^–2 h = 3 m
  E_P = mgh ? = 75 ? × 9,8 ? × 3 ? = 2205 J ?

12.2

• m = 40 kg g = 9,8 m.s^–2 h = 30 m
  E_P = mgh ? = 40 ? × 9,8 ? × 30 ? = 11 760 J ?

12.3

• m = 72 kg v = 30 m.s^–1
  E_K = ½ mv² ?= 0,5 × 72 ? × (30)² ?= 32 400 J ?

12.4

• m = 4000 kg v = 150 m.s^–1 g = 9,8 m.s^–2 h = 5000 m
  E_M = E_K + E_P ?
  = ½ mv2+ mgh ?
  = [0,5 × 4000 ? × (150)² ?] + (4000 x 9,8 ? × 5000 ?)
  = (4,5 × 10⁷) + (1,96 × 10⁷)
  = 6,46 × 10⁷ J ?

12.5

• m = 500 kg g = 9,8 m.s^–2 h = 40 m Because mechanical energy is conserved:
  Ek + Ep1 (just above ground level) + E_k2 + E_p2 (at highest point)
  1 mv² + mgh (just above ground level) = 1 mv² + mgh (at highest point)
  2                                                               2
  1 mv² + 0 (just above ground level) = 0 + mgh (at highest point)
  2