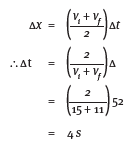Overview

Summary

1 Motion and forces
Mechanics is the branch of physics that focuses on the motion of objects and the forces that act on them. Not all physical quantities can be treated in the same way. Two 2 kg masses lumped together give a bigger mass of 4 kg, but the combined effect of two forces acting on an object in different directions cannot be found by simple addition. It is important to learn how to work with physical quantities such as force before meeting similar difficulties in your study of motion.

When speaking of motion, many people use the words ‘velocity’ and ‘acceleration’ to describe the same thing, but this is a mistake. For example, it is quite common for a moving object to have a high velocity and very little or no acceleration. Getting correct ideas about concepts like this from the start makes things much easier later on. Some aspects of motion can be quite tricky to analyse. So you will be pleasantly surprised to find that straight-line motion at constant speed or with speed that changes by the same amount every second is relatively easy to describe in words, diagrams, graphs and equations.

The study of motion leads on to the energy transfers that cause all the excitement on a roller coaster. Our interest is in the energy possessed by an object because of its position above the ground and the energy it has when it is moving. We will study the interchange between these two energies in roller coasters and some other frictionless systems.

2 Vectors and scalars

• Scalar quantities (for instance, mass, charge, energy, time, distance and speed) have magnitude only.
• Vector quantities (for instance, force, weight, displacement, velocity and acceleration) have both magnitude and direction
• Vector quantities are represented by arrows called vectors.
• In a drawing to scale, the magnitude of a vector quantity is represented by the length of the vector and its direction is indicated by the arrowhead.
• Equal vectors have the same length and direction.
• Negative vectors act in the opposite direction to the chosen positive direction.
• Vectors can be added and subtracted and their magnitudes can be multiplied.
• A resultant vector is the single vector that has the same effect as a number of separate vectors acting together.
• Resultant vectors can be determined:
  • graphically, using the tail-to-head and tail-to-tail methods
  • by calculation.

3 Motion in one dimension

• Motion is measured relative to a frame of reference. A frame of reference has an origin (or reference point) and a set of directions.
• Motion in one dimension is straight-line motion in the forward or backward direction.
• Position is always stated relative to a reference point and may be positive or negative. For position, usually use the symbol x; if motion is vertical, use the symbol y.
• Displacement (∆x or ∆y) is change in position. It is a vector quantity: the straight-line distance from a starting position to a new position, together with the direction.
• Distance (D) is the length of the actual path taken between a starting position and a new position. It is a scalar quantity.
• Average speed (v) is a scalar quantity: the distance travelled divided by the time taken (∆t).
  v = D
       ∆t
• Average velocity is a vector quantity: the displacement divided by the time taken.
  v = ∆x
        ∆t
• Average acceleration (a) is the change in velocity divided by the time taken.
  a = ∆v
        ∆t

3.1 Worked examples

1. Sara runs a 200 m race in 30 s. Calculate her average speed.
   Answer:
   v = D
        ∆t
   = 200
       30
   = 6,67 m.s^–1
2. Calculate Simo’s average velocity if it takes him 8 minutes to walk 400 m east and then 160 m west.
   Answer:
   v = ∆x
         ∆t
   = 240
      480
   = 6,67 m.s^∆1 east
   The direction east is chosen as the positive direction.
   ∆t = 8 × 60 = 480 s ∆x = 400 – 160 = 240 m east
3. A cyclist moving at 12 m.s–1 stops pedalling at the bottom of a gentle slope and coasts to a stop. If this takes 5 s, calculate his acceleration.
   Answer:
   The initial direction of motion is chosen as the positive direction.
   ∆v = final velocity – initial velocity = (0 – 12) = –12 m.s^–1
   a = ∆v
         ∆t
   = 12
       5
   = ∆2,4 m.s^∆2, that is, 2,4 m.s^–2 in the opposite direction to the initial motion

• Acceleration indicates how quickly the velocity is changing, but provides no information about the direction of motion.
• Acceleration is produced by a force, and always has the same direction as the force that is causing it.
• If we take the direction in which a car is facing as the positive direction, then: positive acceleration means there is a forward force acting, which will increase its velocity negative acceleration means there is an opposing force acting on it, which will either decrease its velocity (for instance, if the brakes are applied, or it coasts uphill) or increase its velocity backwards (if the car accelerates in reverse gear).
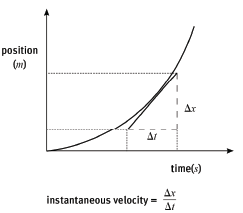
• Instantaneous velocity is the displacement divided by a very small time interval.
• Instantaneous speed is the magnitude of the instantaneous velocity.

4 Motion described in words, diagrams, graphs and equations
4.1 Motion with uniform velocity

• An object moving in a straight line with uniform velocity changes its position by the same amount in equal time intervals.
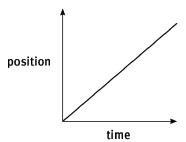
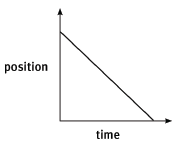
• A position–time graph for motion with uniform velocity is always a straight line with a positive or negative gradient.
• For motion in the positive direction, the graph has a positive gradient.
  
  When motion is in the negative direction, the gradient is negative.
  
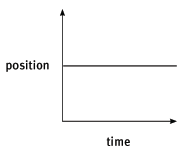
  A position–time graph of a stationary object is horizontal.
  
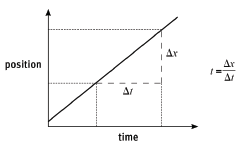
  The gradient of a position–time graph is equal to the uniform velocity.
  
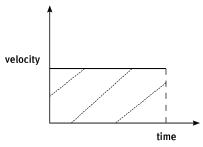
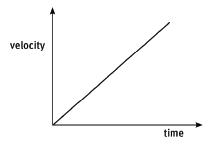
  A velocity–time graph for motion with uniform velocity is horizontal.
  
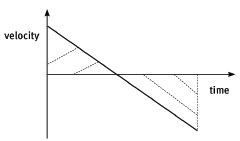
• The area under a velocity–time graph is equal to the displacement. The area under the graph is rectangular in shape. Motion is in the positive direction when the area under the graph is positive (above the horizontal time axis) and motion is in the negative direction when the area under the graph is negative (below the time axis).

4.2 Motion with uniform acceleration

• An object moving with uniform acceleration has a velocity that changes in magnitude by the same amount in equal time intervals.
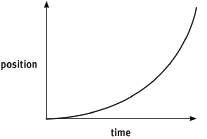
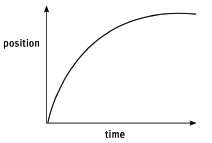
• A position–time graph for motion with uniform acceleration is never a straight line. The gradient of the graph changes at a constant rate.
• For motion in the positive direction, the gradient of the graph increases steadily if the velocity is increasing.
  
• For motion in the positive direction, the gradient of the graph decreases steadily if the velocity is decreasing.
  
• The gradient of the tangent drawn to a position–time graph at a particular time is equal to the instantaneous velocity.
  
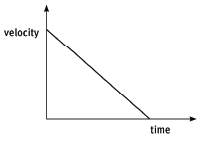
• A velocity–time graph for motion with uniform acceleration is always a straight line with a positive or negative gradient.
• For motion in the positive direction, the graph has a positive gradient if the velocity is increasing.
  
• For motion in the positive direction, the graph has a negative gradient if the velocity is decreasing.
  
• The gradient of a velocity–time graph is equal to the uniform acceleration.
• The area under a velocity–time graph is equal to the displacement. For motion with uniform acceleration, the area under the graph is triangular in shape. Motion is in the positive direction when the area under the graph is positive and motion is in the negative direction when the area under the graph is negative.
  
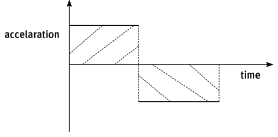
• An acceleration–time graph for motion with uniform acceleration is horizontal.
• The area under an acceleration–time graph is equal to the change in velocity. The area under the graph is rectangular in shape. For motion in the positive direction, the change in velocity is positive when the area under the graph is positive and the change in velocity is negative when the area under the graph is negative.
  
• Roads are safer when drivers understand the relationship between speed and stopping distance, when drivers are in full control of their faculties, when brakes are in good condition, when road conditions are favourable and when vehicles are fitted with safety features.

4.3 Kinematics equations

• Equations of uniform motion are used to solve problems involving motion in one dimension.
• The symbols used in the equations are:
  • ∆x: displacement (or use ∆y it the change in position is vertical)
  • ∆t: time a: unifom acceleration
    v_f : initial velocity v_f : final velocity
• The equations are:
  

4.3.1 Worked examples
1 Jane cycles along a straight, level road at 4 m.s^–1. Then she accelerates uniformly at 0,5 m.s^–2 for 12 s. Calculate:
1.1 the final velocity
1.2 the displacement while she accelerates.

Answers:
Take the initial direction of motion as the positive direction.
1.1

• vi = 4 m.s^–1 a = 0,5 m.s^–2 ∆t = 12 s
  vf = vi = a∆t²
  = 4 + (0,5 x 12)
  = 10m.s–1 in the direction of motion

1.2

• vi = 4 m.s^–1 a = 0,5 m.s^–2 ∆t = 12 s
  ∆x = v ∆t + 1 a∆t²
                    2
  = (4 12) +{0,5 × 0,5 × (12)²}

2 Joe cycles along a straight, level road at 15 m.s^–1. Then he stops pedalling and slows down uniformly over a displacement of 52 m. If his velocity falls by 1 m.s^–1 every second, calculate:
2.1 the final velocity after 52 m
2.2 the time that he takes to cover the 52 m.

Answers:
Take the initial direction of motion as the positive direction.
2.1

• vi = 15 m.s^–1 a = –1 m.s^–2 ∆x = 52 m
  v _f² = v_t² + 2a∆x
  = (15)² + {2 ×(–1) × 52}
  = 225 – 104
  ∴ vf = √121
  = 11m.s^-1 in the direction of motion

2.2

• v_i = 15 m.s^–1       vf = 11 m.s^–1 a = –1 m.s^–2
  

5 Energy

• The gravitational potential energy of an object is the energy it has because of its position in the Earth’s gravitational field relative to a selected reference point.
• Gravitational potential energy is calculated using the formula:
  E_P = mgh
• Kinetic energy is the energy possessed by an object as a result of its motion.
• Kinetic energy is calculated using the formula:
  EK = ½ mv²
• Mechanical energy (E_M) is the sum of gravitational potential energy and kinetic energy:
  E_M = E_K + E_P
• Energy cannot be created or destroyed. It can only be changed from one form into another.
• In the absence of air resistance, the mechanical energy of an object moving in the Earth’s gravitational field is conserved.
• When energy transfers happen and mechanical energy is conserved, use the equation:
  E_K1 + E_P1 = E_K2 + E_P2

5.1 Worked examples
1 A boy of mass 50 kg is ready to jump from a bridge into the water 4,9 m below. What is his potential energy:
1.1 relative to the bridge?
1.2 relative to the water surface?
Answers:
1.1 0
1.2

• m = 50 kg g = 9,8 m.s^–2 h = 4,9 m
  E_P = mgh
  = (50 × 9,8 × 4,9)
  = 2401 J

2 After falling for 1 s, the boy in the previous example splashes into the water with a speed of 9,8 m.s–1. Calculate his kinetic energy as he strikes the water surface.
Answer:

• m = 50 kg v = 9,8 m.s^–1
  E_K = ½ mv²
  = [0,5 × 50 × (9,8)²]
  = 2401 J

3 Calculate the mechanical energy of a sledgehammer of mass 3 kg moving downwards at 6 m.s^–1 and 0,5 m above the ground.
Answer:

• m = 3 kg v = 6 m.s^–1  g = 9,8 m.s^–2    h = 0,5 m
  E_M = E_K + E_P
  = ½ mv² + mgh
  = [0,5 × 3 × (6)²] + (3 × 9,8 × 0,5)
  = 68,7 J