Overview

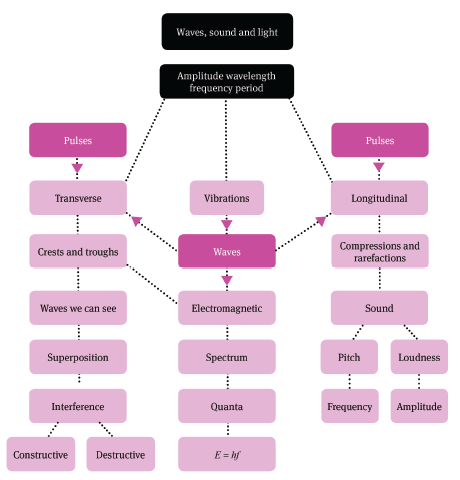
Summary

1 Transverse pulses and waves
1.1 Properties of transverse pulses and waves

• A pulse is a single disturbance in a medium. A single crest is a transverse pulse. A single trough is also a transverse pulse.
• In a transverse pulse or wave, the particles of the medium vibrate at 90° to the direction in which the pulse or wave moves.
• The amplitude of a pulse is the maximum displacement from the position of rest of a particle in the medium.
• A wave is made up of one pulse after another.
• The ‘hump’ in a transverse wave is called a crest.
• The ‘hollow’ in a transverse wave is called a trough.
• Continuous transverse waves are produced by continuous vibrations of the medium.
• A vibration is a regular to-and-fro movement (up-and-down or forwards-and- backwards).
• The rest position of a vibrating object (also called the equilibrium position) is the position that it would be in when not vibrating.
• One complete vibration (also called one oscillation) is one complete to-and-fro movement. It is the movement from the rest position to the furthest point in one direction, then to the furthest point in the opposite direction, then back to the rest position.
• One complete vibration (or one oscillation) of the end of a slinky spring will produce one wavelength in the spring.
• Particles in a medium are in phase if they are vibrating perfectly in step with one another.
• Particles in a medium that are not vibrating perfectly in step with one another are out of phase. Two particles are completely out of phase if they are moving oppositely, with one reaching the crest at the same instant that the other reaches the trough.

1.2 Wavelength, frequency, amplitude, period, wave speed

• Wavelength (λ) is the distance between two consecutive points that are in phase. For transverse waves, wavelength is the distance between two successive crests or two successive troughs. The unit is metres (m). If the wavelength is given in any other unit (for instance, mm or nm), it must be converted to metres when doing a calculation.
• Frequency (f) is the number of wavelengths passing per second. It equals the frequency of the vibration making the waves. The unit is s^–1 (per second). 1 s^–1 is called a hertz (Hz).
• The amplitude of a wave is the maximum distance that a point in a wave moves from its rest position. This equals the distance from the rest position to the top of a crest or to the bottom of a trough. The unit is metres (m).

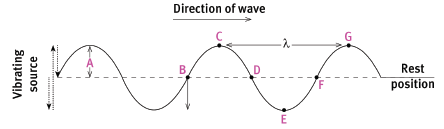
Distance A is the amplitude of the wave. Each point in the medium simply vibrates up and down. Point B must be moving down for the wave to be moving to the right. Point B and F and points C and G are in phase. Points B and D and points C and E are completely out of phase. Distance CG and distance BF are equal and are the wavelength.

• The speed of a wave (v) is the distance moved by any pulse in the wave per second. The speed can change as the medium changes. The unit is metres per second (m.s^–1). If the speed is given in any other unit (for instance, km hr^–1), it must first be converted to m.s^–1 before doing a calculation.
• Speed is calculated using the formula: speed (in m.s^–1) =           Distance moved (in m)      
                                                                                                             time taken (in s)
• The wave equation relates the above three quantities: v = f λ
• The period (T) of a wave is the time taken for one wavelength to pass. The unit is seconds (s). T = 1 / f
• Period and frequency are inversely proportional to each other. If the frequency is doubled, the period is halved. It also equals the period of the vibration making the wave.
• If T = 1 / f , it follows that f = 1 / T.
• If we take the wave equation v = f λ and substitute 1 / T for f, we have v = λ / T.

1.2.1 Worked example
A transverse wave is set up in a slinky spring lying on a long table. The wavelength is 540 mm. One wavelength passes a mark on the table every 0,8 s.
Calculate:

1. the frequency of the wave
2. the speed of the wave.

Answers:

1. T = 0,6 s f = ?
   f = 1  =  1  
        T    0,8
   = 1,25 Hz
2. f = 1,25 Hz            λ = 540 mm = 0,54 m               v = ?
   v = f λ
   = 1,25 × 0,54
   = 0,675 m.s^–1

1.3 Superposition of pulses

• Superposition is the addition of the amplitudes of two pulses that occupy the same space at the same time. If a crest is considered positive, then a trough is negative.
• When waves meet, they interfere.
• Crest meeting crest or trough meeting trough results in a bigger amplitude – constructive interference.
• Crest meeting trough results in a smaller amplitude – destructive interference.
• Two pulses will cancel out to produce zero amplitude only if:
  • one is a crest, the other a trough
  • their amplitudes are equal
  • their pulse lengths are equal.

2 Longitudinal waves and sound
2.1 Longitudinal pulses and waves

• A pulse is a single disturbance in a medium. A single compression (particles close together) or a single rarefaction (particles far apart) are each longitudinal pulses.
• The amplitude of a pulse is the maximum displacement from the position of rest of a particle in the medium. So it is the distance from the rest position to the centre of a compression, or the distance from the rest position to the centre of a rarefaction.
• In a longitudinal wave, the particles of the medium vibrate in line with the direction in which the wave moves.
• Longitudinal waves are made up of alternate compressions (particles close together) and rarefactions (particles far apart).
• Wavelength (λ) is the distance between two consecutive points that are in phase. For longitudinal waves, wavelength is the distance between two successive compressions or two successive rarefactions. The unit is metres (m). If the wavelength is given in any other unit (for instance, mm or nm), it must be converted to metres when doing a calculation.
• Frequency (f) is the number of wavelengths passing per second. It equals the frequency of the vibration making the waves. The unit is s^–1 (per second). 1 s^–1 is called a hertz (Hz).
• The amplitude of a wave is the maximum distance that a point in a wave moves from its rest position. For a longitudinal wave, it is the distance from the rest position to the centre of a compression or to the centre of a rarefaction. The unit is metres (m).
• The period and frequency of a longitudinal wave have the same meaning as for a transverse wave. Period is the time taken for one wavelength to pass, for instance, the time between two successive compressions, measured in seconds. Frequency is the number of wavelengths that pass per second, measured in Hz.
• The equations T = 1 / f and v = f λ are applied as for transverse waves.

2.2 Sound waves

• Only vibrating objects produce sound. Energy is therefore needed to produce sound.
• A material medium is required for sound to move. Sound cannot pass through a vacuum.
• Sound energy moves through a medium as longitudinal waves. Alternate compressions and rarefactions pass through the medium.
• The speed, frequency and wavelength of sound are related by the equation:
  Speed = frequency × wavelength
  v = f λ
• The speed of sound in air is approximately 340 m.s^–1. The speed is dependent on the medium and its temperature.
• Solids transmit sounds best, gases worst. The same sound is heard loudest through solids, next loudest through liquids and softest through gases.
• Sound moves fastest through solids and slowest through gases. In gases, the greater the mass of the gas molecules, the slower the sound. In air, the higher the temperature the faster the sound.

2.3 Pitch and loudness

• The frequency of a sound wave is determined by the frequency of the vibration that causes it. If the sound wave passes into another medium, say from air into water, the speed of the wave changes, but the frequency stays the same.
• The pitch of a note is its position on a musical scale. As the frequency of a sound wave increases, so the pitch rises.
• Loudness is determined by the amplitude of the sound wave. The greater the amplitude, the louder the sound.
• Ultrasound has frequencies between 20 kHz and 100 kHz, higher than the range of human hearing. Ultrasound is used to produce internal images of the body (for instance, of a baby in the womb). The sound is reflected differently by the different layers in the body.

3 Electromagnetic radiation
3.1 Wave nature and spectrum

• The spectrum of visible light is only a small part of a broad range of waves that travel through a vacuum at the speed of light. The full range is called the electromagnetic spectrum.
• Electromagnetic waves are produced by accelerating charges. For example, in a radio aerial, changing electric fields accelerate electrons back and forth. This produces a changing magnetic field at right angles to the aerial. This in turn produces changing electric fields at right angles, and the process continues with each field generating the other. The crests and troughs in the wave indicate points where the electric or magnetic fields are strongest.

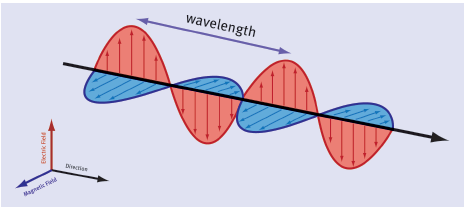
• Electromagnetic waves are transverse and consist of changing electric fields and magnetic fields at 90° to each other.
• Electromagnetic waves travel through space at 3 × 10⁸ m.s^–1. The wave equation c = f λ applies.
• Different sections of the spectrum have different names. In order of increasing wavelength (or decreasing frequency), these are: gamma rays, X-rays, ultraviolet light, visible light, infrared, microwave, TV and radio.
• Gamma rays are produced by radioactive material. They have the highest frequency and the highest energy and are the most penetrative and the most dangerous. They can destroy human cells and cause cancer. Radio waves at the opposite end of the spectrum are far less penetrative and not dangerous.
• X–rays are produced when high-speed electrons strike a metal plate. They can be used to produce a photographic image of the human body. They cannot pass through lead.
• Ultraviolet radiation is produced by very hot objects. Ultraviolet rays are very harmful to the eyes, cause tanning and can cause skin cancer. Some chemicals fluoresce in UV light.
• Infrared radiation is heat radiation, produced by vibrating atoms and molecules in hot objects. TV remotes work by sending out infra-red pulses.

3.2 The wave and particle nature

• Electromagnetic waves are radiated in packages, called quanta. A quantum of light is called a photon.
• Electromagnetic radiation has both a wave nature (transverse electric and magnetic fields) and a particle nature (quanta of energy). Radio waves have such long wavelengths that their particle nature is negligible. Gamma rays have such short wavelengths that their wave nature is negligible. Visible light (in the middle of the electromagnetic spectrum) behaves both as waves and as particles. This is known as the dual nature of light.
• The energy of a quantum can be calculated using the equation:
  E = h f = h c / λ
  where h = 6,63 × 10^–34 J.s (Planck’s constant) and c = 3 × 10⁸ m.s^–1

3.2.1 Worked Examples

1. The energy of a photon of light is 5,3 × 10^–19 J. Calculate the frequency of the light waves.
2. Calculate the energy of a microwave quantum of wavelength 0,2 m.

Answers:

1. E = 5,3 × 10^-19
   E = h f            f = E / h = 5,3 × 10^-19 / 6,63 × 10^–34
   f = 7,99 × 1014 Hz
2. E = hc / λ =  (6,63 × 10^–34) × (3 × 10⁸)
                                        0,2
   E = 9,95 × 10^–25 J